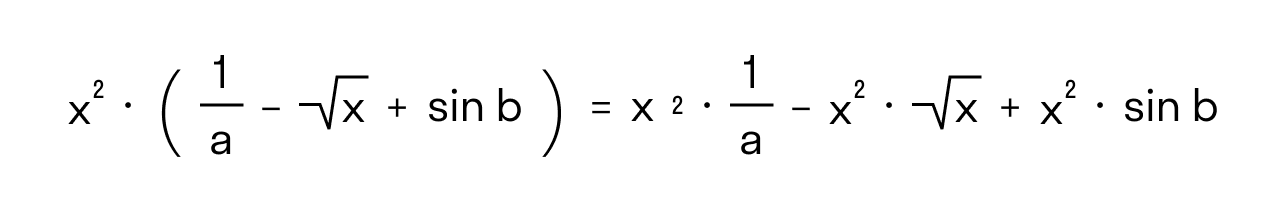Как объяснить решение уравнений со скобками

Овладение детьми способом решения уравнений в начальной школе создает прочную основу для дальнейшего обучения алгебры, химии, физики и других предметов.

Начиная с 3-го класса, ученикам встречаются сложные уравнения, но справиться с ними очень просто.

Дети уже умеют решать простые уравнения, читай об этом здесь.

А эта статья будет посвящена решению сложных уравнений в 2-3 действия.

Очень часто родители, желая помочь, объясняют так: вот смотри, сейчас вот это число перенести в другую часть от знака равенства, надо поменять знак на противоположный: было умножение, меняем на деление; было сложение меняем на вычитание.

В начальной школе это объяснение не срабатывает, т.к. ребенок не знаком с законами алгебры.

Как сложное уравнение привести к тому, которые мы уже умеем решать, а именно к уравнению в 1 действие?

Рассмотрим уравнение в 2 действия:

х + 56 = 98 — 2 — оно достаточно легкое.

Здесь особого труда не будет в решении, потому что ребенок сразу догадается, что сначала надо 98-2.

х + 56 = 98 — 2

х + 56 = 96 – это простое уравнение. А его решаем очень быстро!

Сейчас мы рассмотрим уравнение:

Такое уравнение можно решить несколькими способами.

1. У нас здесь неизвестное число х. Мы не знаем, что спрятано за этим числом.

А когда к х + 5 – это число тоже известно.

Закроем его и пусть это будет другое число, например b .

Мы видим, что у нас получилось самое простое уравнение в 1 действие.

2 • b = 30

А чтобы найти а, нам нужно 30 : на 2.

А b не что иное, как х + 5.

х + 5 = 30 : 2

х + 5 = 15

х = 15 – 5

х = 10

Проверку делаем как обычно: переписываем первое уравнение: 2 • (10 + 5) = 30.

30 – переписываем, а левую часть считаем — будет 30.

30 = 30, значит, уравнение решили правильно.

При решении таких сложных уравнений самое главное – понять, что заменить на другое неизвестное число. Когда в уравнении всего 2 действия – это очень просто.

1. Более удобно и понятно, как показывает практика, если использовать решение сложных уравнений на основе зависимости между компонентами действий.

Наше уравнение 2 • (х + 5) = 30 читаем так: число 2 умножить на сумму х и пяти, получится 30. В данном случае – нам неизвестна сумма, чтобы ее найти, надо 30:2.

48 : (16 – а) = 4.

Если опять заменять часть уравнения другим неизвестным числом, можно запутаться. Поэтому легче использовать взаимосвязи компонентов и результата действия: число 48 разделить на разность.

Нам неизвестна разность, поэтому сначала нужно узнать чему она равна. Надо 48 : 4.

16 — а = 48 : 4

16 — а = 12 – это простое уравнение.

а = 16 — 12

а = 4

Проверка: 48 : (16 — 4) = 4

Давайте посмотрим еще одно:

Из 96 надо вычесть разность с и 16. Чтобы найти разность, надо 96-94.

Проверка: 96 — (16 — 14) = 94

А сейчас мы переходим к тем уравнениям, у которых не 2, а 3 действия. Как же нам поступать в этом случае? При решении таких сложных уравнения используем знания порядка выполнения действий в выражениях со скобками и без них.

Рассмотрим уравнение: 36 – (8 • у + 5) = 7

Прежде всего, нужно внимательно оценить левую часть уравнения: ту, которая с неизвестным числом. Вы должны четко себе представить какое вы будете делать действие первым, какое – вторым, какое – третьим: сначала делается умножение, потом сложение и последним – вычитание.

И вот то, которое вы будете делать третьим, с него и начнем, т.е. начинаем упрощать уравнение с последнего действия. Последнее действие – вычитание. С него и начнем: из числа 36 вычесть то, что в скобках и получим 7.

Значит, то что в скобках – вычитаемое, чтобы его найти, надо 36 — 7.

По правилам математики в данной записи скобки – не ставим.

8 • у + 5 = 29 – уравнение сложное. Нужно его упростить. Данное уравнение читаем так: к произведению 8 и у прибавили 5 и получилось 29. Нам неизвестно произведение, чтобы его найти, надо 29-5.

8 • у = 24 – это уравнение простое.

Проверка: 36 — (8 • у + 5) = 7 . Правую часть – 7 — переписываем, а левую считаем.

Итак: 7 = 7. Значит, уравнение решили правильно.

(36 + d) : 4 + 8 = 18. Определяем порядок действий: первое – сложение в скобках, второе – деление, третье сложение вне скобок. Значит, все, что до 8 – это первое слагаемое, чтобы его найти, надо 18 — 8

(36 + d) : 4 = 18 — 8

(36 + d) : 4 = 10 – уравнение сложное, теперь последнее действие — :, значит

36 + d = 40 – уравнение простое и его мы решаем легко!

Для удобства и быстроты решения сложных уравнений можете пользоваться данной памяткой

Дело в том, что при кажущейся сложности, если внимательно изучить все приемы, которые я вам сегодня показала, эти уравнения дети будете щелкать как семечки. Обязательно напишите в комментариях, какой способ вам более удобен.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 58

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Раскрытие скобок

О чем эта статья:

Видео:Решаем уравнения со скобками.Правило раскрытия скобок.Скачать

Понятие раскрытия скобок

В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.

Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений.

Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:

Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.

Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.

В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:

• знаки плюс или минус перед скобками, которые заключают сумму или разность, например, (a + 7) и -(-3 + 2a — 12 — b);
• произведение числа, одной или нескольких букв и суммы или разности в скобках, например, 3(2 — 7), (3 — a + 8c)(-b) или -2a(b + 2c — 3m).

Раскрытие скобок также можно рассматривать шире.

Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:

Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:

Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.

Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств. Например, вот так:

• 5 — (3 — (2 — 1)) = 5 — (3 — 2 + 1) = 5 — 3 + 2 — 1

Видео:Раскрытие скобок. 6 класс.Скачать

Первое правило раскрытия скобок

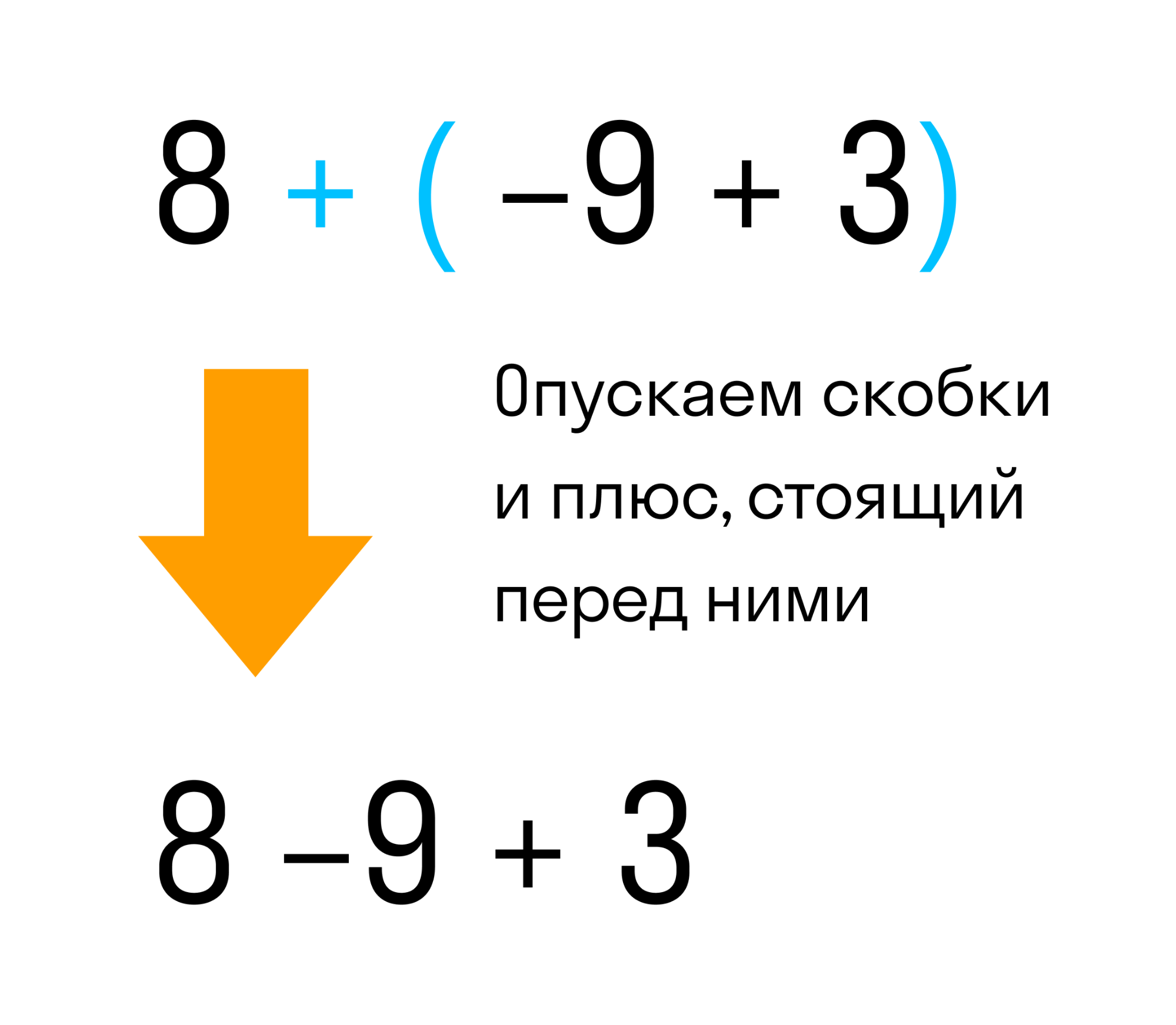
Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.

Первое правило раскрытия скобок

Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак.

Формула раскрытия скобок

Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:

Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.

Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

Потренируемся применять правило на примерах.

Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)

Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:

Пример 2. Раскрыть скобки в выражении 6 + (−2)

Перед скобками стоит плюс, значит применим то же правило:

Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.

В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.

Идем дальше. Теперь упростим выражение 2a + a − 5b + b.

Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

• 2a + a — 5b + b = 2a + a + (-5b) + b = (2 + 1) * a + (-5 + 1) * b = 3a + (-4b)

Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.

Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.

После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:

Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:

• 2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6

Пример 3. Раскрыть скобки 6 + (−3) + (−2)

В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:

Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.

Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.

Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

• 1 + (2 + 3 − 4) = 1 + 2 + 3 − 4

Пример 4. Раскрыть скобки в выражении (−7)

Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:

Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)

Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:Уравнения. 5 классСкачать

Второе правило раскрытия скобок

Здесь рассмотрим второе правило раскрытия скобок. Звучит так:

Второе правило раскрытия скобок

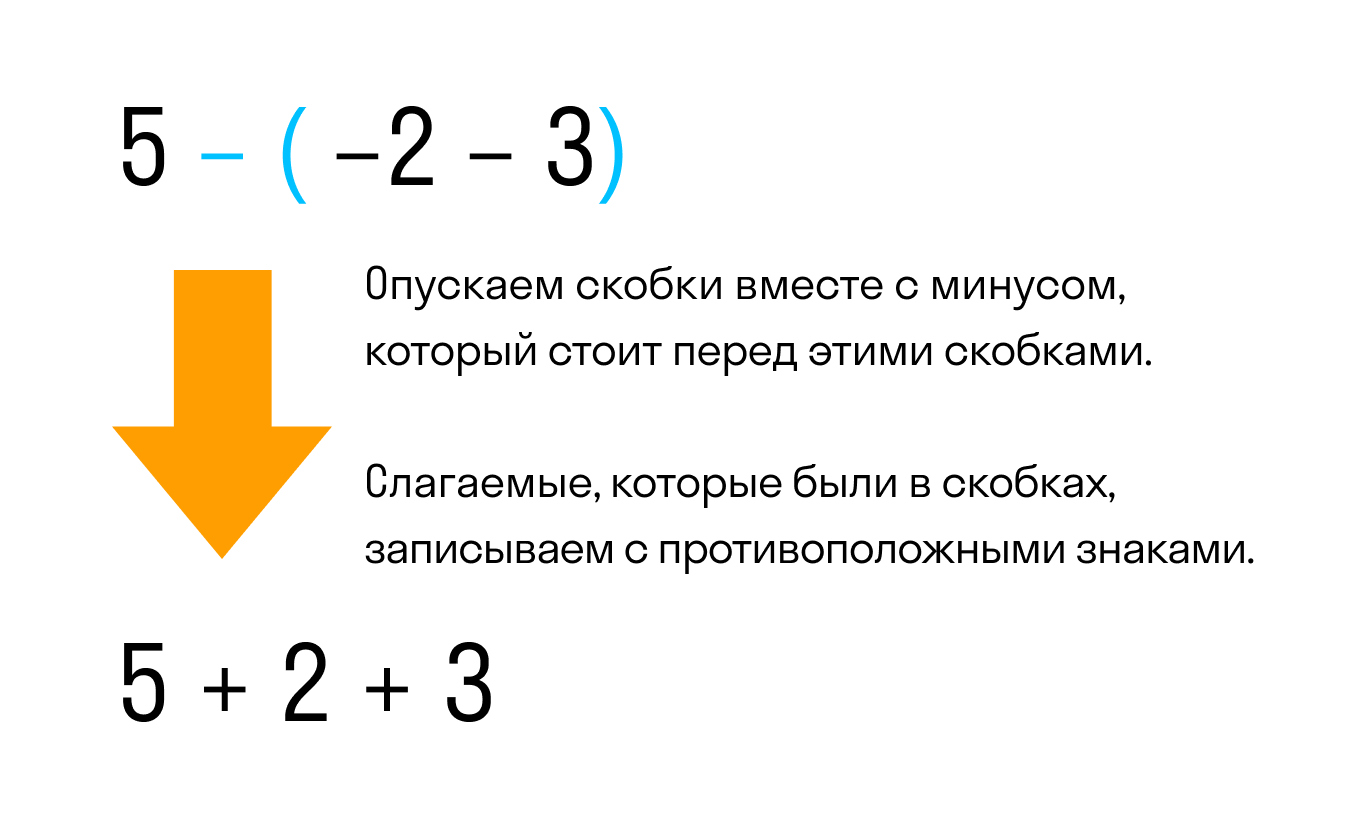
Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный.

Формула раскрытия скобок

Например, раскроем скобки в выражении 5 − (−2 − 3)

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.

Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:

Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

18 − (−1 − 5) = 18 + 1 + 5

Пример 2. Раскрыть скобки −(−6 + 7)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)

Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:

−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2

Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

a − (3b + 3) + 10 = a − 3b − 3 + 10

Видео:УРАВНЕНИЯ СО СКОБКАМИ. Примеры | МАТЕМАТИКА 5 классСкачать

Другие правила раскрытия скобок

Правило раскрытия скобок при делении

Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок.

Формула раскрытия скобок

(a + b) : c = a/c + b/c.

Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.

Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.

Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число:

Далее умножим скобку на число:

• (x + 2) * 3/2 = x * 3/2 + 2 * 3/2.

Правило раскрытия скобок при умножении:

Если перед скобками стоит знак умножения — каждое число, которое стоит внутри скобок, нужно умножить на множитель перед скобками.

Формула раскрытия скобок

Пример 1. Раскрыть скобки 5(3 − x)

В скобке у нас стоят 3 и −x, а перед скобкой — пятерка. Значит, каждый член скобки нужно умножить на 5:

Знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.

Пример 2. Упростить выражение: 5(x + y) − 2(x − y)

Как решаем: 5(x + y) − 2(x − y) = 5x + 5y − 2x + 2y = 3x + 7y.

Видео:№2 Квадратное уравнение со скобками (х-1)(x-2)=-6х Как избавиться от скобок в уравнении Как решить уСкачать

Таблица с формулами раскрытия скобок

Эти таблицы с правилами раскрытия скобок можно распечатать и обращаться к ним, когда возникнут сомнения в ходе решения задачки.

Правила раскрытия круглых скобок вида (-a), в которых находится одночлен

Правила раскрытия круглых скобок, в которых находится многочлен

Скобки убирают, знаки всех слагаемых в скобках не меняют, если:

• перед скобкой стоит знак плюс:

a + (b — c + d) = a + b — c + d

• выражение начинается со скобки и перед ней нет знака:

Скобки убирают, знаки всех слагаемых в скобках меняются на противоположные, если:

• перед скобкой стоит знак минус:

a — (b — c + d) = a — b + c — d

• выражение начинается с минуса перед скобкой:

-(a + b — c) + d = -a — b + c + d

Раскрытие круглых скобок при умножении одночлена на многочлен

a + b(c + d — f + e) = a + bc + bd — bf + be

a + b(c + d — f + e) = a + bc + bd — bf + be

-a(b + c — d) + f = -ab — ac + ad + f

Раскрытие круглых скобок при умножении многочлена на многочлен

(a + b)(c — d) = a(c — d) + b(c — d) = ac — ad + bc — bd

(-a + b)(c + d) = -a(c + d) + b(c + d)= -ac — ad + bc + bd

Раскрытие круглых скобок при возведении многочлена в степень

(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b)= a2 + ab + ab + b2 = a2 + 2ab + b2

Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Скобка в скобке

В 7 классе на алгебре можно встретить задачи со скобками, которые вложены внутрь других скобок. Вот пример такого задания:

• упростить выражение 7x + 2(5 − (3 x + y)).

Чтобы успешно решать подобные задания, нужно:

• внимательно разобраться со скобками — какая в какой находится.
• раскрывать скобки последовательно, начиная с самой внутренней.

При этом важно при раскрытии одной из скобок не трогать все остальное выражение и просто переписывать его, как есть. Разберем подробнее тот же самый пример.

Пример 1. Раскрыть скобки и привести подобные слагаемые 7x + 2(5 − (3x + y))

Начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относится – это сама скобка и минус перед ней. Всё остальное переписываем также как было.

• 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y).

Теперь раскроем вторую скобку, внешнюю:

• 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y) = 7 x + 2 * 5 − 2 * 3 x − 2 * y.

Упростим получившееся выражение:

• 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y) = 7 x + 2 * 5 − 2 * 3 x − 2 * y = 7x + 10 − 6x − 2y.

• 7x + 10 − 6x − 2y = x + 10 − 2y

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Порядок раскрытия скобок

Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида. То есть в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.

Порядок раскрытия скобок согласован с порядком выполнения действий:

• возвести многочлены в скобках в натуральную степень;
• слева направо провести умножение и деление;
• когда в скобках останутся только слагаемые, раскрыть скобки и привести подобные.

Пример 1. Раскрыть скобки и упростить выражение:

-(2a + 5b) + (3a — 2b + 1) — (2a + 4) = -2a — 5b + 3a — 2b + 1 — 2a — 4 = (-2a + 3a — 2a) + (-5b — 2b) + (1 — 4) = -a — 7b — 3

Пример 2. Доказать, что при любых значениях переменной a значение выражения 3(2a — 7) — (a + (5a — 4)) — отрицательно.

33(2a — 7) — (a + (5a — 4)) = 3(2a — 7 ) — (a + 5a — 4)= 6a — 21 — a — 5a + 4 = (6a — a — 5a) + (-21 + 4) = -16/p>

Значение выражения не зависит от переменной и всегда отрицательно. Что и требовалось доказать.

Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Задачи для самостоятельного решения

На алгебре в 6 и 7 классе придется решать задачки с раскрытием скобок много и часто. Поэтому лучше запомнить правила и практиковаться уже сейчас.

Задание 1. Раскройте скобки в выражении: 2 + (6 + 3) + 2 — (1 + 1)

Задание 2. Раскройте скобки в выражении: — 21 + 14 + (-1 + 5) — 11 + ( 3 + 2)

Задание 3. Раскройте скобки в выражении: 3 * (-4m + 3n — 5)

Задание 4. Раскройте скобки в выражении: -(12a — 5b — 2)

Задание 5. Раскройте скобки в выражении: 3(x — 9)

Задание 6. Раскройте скобки:

Задание 7. Раскройте скобки:

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Памятка : «Решение уравнений», 5 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

(Х – 87) – 27 = 36; Х-87 в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое

Х – 87 = 63; х в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое

Проверка: (150 – 87) – 27 = 36;

87- ( 41 + У ) = 22; 41 + У в уравнении является вычитаемым . Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность

41 + У = 65; У в уравнении является слагаемым. Чтобы найти неизвестное слагаемое , нужно из суммы вычесть известное слагаемое

Проверка: 87- ( 41 + 24 ) = 22;

(у – 35) + 12 = 32; у – 35 в уравнении является слагаемым. Чтобы найти неизвестное слагаемое , нужно из суммы вычесть известное слагаемое

у – 35 = 20; у в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое

(237 + х) – 583 = 149;

468 – ( 259 – х) = 382;

(237 + х) – 583 = 149;

237 + х = 149 + 583;

(237 + х) – 583 = 149;

237 + х – 583 = 149;

х – (583 – 237) = 149;

468 – ( 259 – х) = 382;

259 – х = 468 – 382;

468 – ( 259 – х) = 382; 468 – 259 + х = 382;

Решение уравнений, приведение подобных слагаемых

Пример 1: 8х-х=49 ; сначала запишем знаки умножения,

8*х-1*х=49 ; затем воспользуемся распределительным свойством (вынесем общую переменную за скобки)

Х*7=49 ; х является неизвестным множителем . Чтобы найти неизвестный множитель , нужно произведение разделить на известный множитель

Пример 2: 2х+5х+350=700 ; воспользуемся распределительным свойством (вынесем общую переменную за скобки)

Х*(2+5)+350=700 ; приведем подобные слагаемые (т.е. сложим числа в скобках)

7х является неизвестным слагаемым . Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое

7х=350; х является неизвестным множителем . Чтобы найти неизвестный множитель , нужно произведение разделить на известный множитель

2*50 + 5*50 + 350 = 700;

100 + 250 + 350 = 700;

Пример: 270: х + 2 = 47;

( 270 : х — является слагаемым.

Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое

( х является делителем . Чтобы найти неизвестный делитель , нужно делимое разделить на частное)

Пример: а : 5 – 12 = 23;

Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое )

( а является делимым. Чтобы найти неизвестное делимое , нужно частное умножить на делитель .

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 956 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 685 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 314 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Уравнения со скобками - 5 класс (примеры)Скачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 573 201 материал в базе

Материал подходит для УМК

«Математика», Виленкин Н.Я., Жохов В.И. и др.

Другие материалы

• 09.12.2019
• 254
• 2

• 08.12.2019
• 253
• 0

• 19.11.2019
• 200
• 2

• 18.11.2019
• 898
• 7

• 18.11.2019
• 309
• 0

• 17.11.2019
• 317
• 0

• 17.11.2019
• 287
• 10

• 17.11.2019
• 210
• 4

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 15.12.2019 55340
• DOCX 17.4 кбайт
• 6499 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Кретинина Светлана Сергеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 4 года и 5 месяцев
• Подписчики: 0
• Всего просмотров: 59999
• Всего материалов: 9

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

В России могут объявить Десятилетие науки и технологий

Время чтения: 1 минута

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

В Ленобласти школьники 5-11-х классов вернутся к очному обучению с 21 февраля

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📽️ Видео

Решение уравнений, 6 классСкачать

Как решить сложные уравненияСкачать

Уравнения для 2 класса Математика Как объяснить ребенку решение уравнений 2 классСкачать

Уравнение с раскрытием скобок. #математика #алгебра #уравнение #скобки #минус #simplemathСкачать

Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Решение уравнений со скобками (3 класс)Скачать

РЕШЕНИЕ УРАВНЕНИЙ |ПОДРОБНОЕ ОБЪЯСНЕНИЕ КАК РЕШИТЬ УРАВНЕНИЯ / ПРОСТЫЕ УРАВНЕНИЯ 2 КЛАСС МАТЕМАТИКАСкачать

Как решать #уравнения, что делать если перед скобкой #минус, как открыть скобку в уравнении #5классСкачать