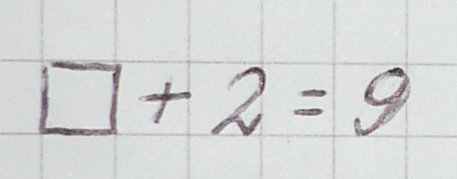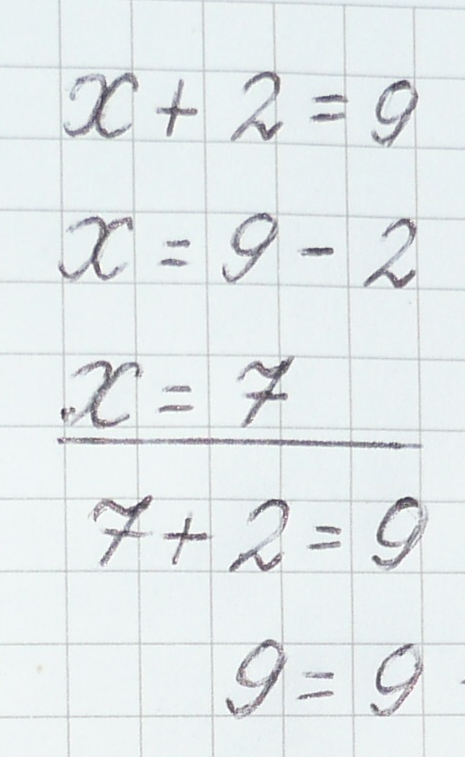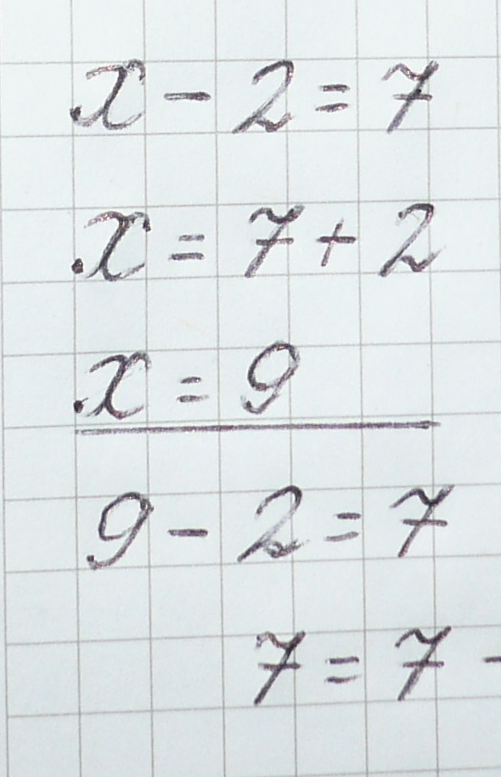Как объяснить первокласснику решение уравнений

С уравнениями ученики знакомятся в 1 классе. Сначала решают примеры с окошком: выполняют действия с числами и задания на нахождение неизвестного числа, например было равенство:

И одно число решили спрятать:

Нам нужно догадаться, что за число спрятали?
Здесь прекрасно видно, чтобы найти неизвестное число, нужно из 9 — 2
Искомое число – 7.

В нашем равенстве – искомое число называют неизвестным числом.
А равенство, в котором одно число стало неизвестным, называется УРАВНЕНИЕМ.
Никто из вас никогда не видел, чтобы уравнения делали с «окошком». Это неудобно. Гораздо проще неизвестное обозначать буквами.

Неизвестное число обозначают маленькими латинскими буквами

или любой другой буквой.

И этому числу дают имя – корень уравнения.
Давайте посмотрим записи:
8+х
8+х>5
8+х =10
Только третья запись — уравнение. Потому что здесь есть неизвестное число и знак =.
Нам необходимо узнать это число.
Найти все значения х, при котором равенство будет верным — значит, решить уравнение, т.е. найти его корень.

При решении уравнения учитываем взаимосвязи между целым и частью:
— чтобы найти целое, надо сложить части;
— чтобы найти часть, надо из целого вычесть другую часть.

Если вы хотите более подробно узнать, как связаны целое и части, читайте тут.

Решение записывается так:

Корень пишем на следующей строке и подчеркиваем прямой линией.

Корень уравнения = 7, следовательно, наше уравнение решено.
Нам обязательно нужно проверить правильно мы нашли корень уравнения или нет.
Уравнение без проверки – это не уравнение.
Итак, в нашем уравнении корень –7, мы его подчеркнули, а теперь сделаем проверку. Для этого мы переписываем первую строку уравнения, но вместо неизвестного поставим значение корня.
Теперь: знак = пишем под знаком =. Число, записанное справа от знака равно: 9 – переписываем. Выражение, которое находится слева от знака равно: 7 + 2 – считаем. Получится 9. Это число 9 записываем слева от знака =.
Читаем выражение: 9 = 9. Значит, уравнение решили правильно.

Решим еще одно уравнение:

Ученикам начальной школы нужно обязательно овладеть математической речью. Для этого нужно знать, как называются компоненты при различных действиях, и как находится неизвестный компонент:

Если из суммы вычесть одно из слагаемых, то получится другое слагаемое.
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 66

Видео:РЕШЕНИЕ УРАВНЕНИЙ ЛЕГКО ! 1 КЛАСС МАТЕМАТИКА УРАВНЕНИЯ - ПЕТЕРСОН / ОБЪЯСНЕНИЕ КАК РЕШАТЬ УРАВНЕНИЯСкачать

Как научить детей решать задачи по математике: советы именитых педагогов и простых мам

Научить детей решать задачи по математике — дело учителя, но и родители не должны оставаться в стороне, если их чадо «тормозит» в этом вопросе. Одним учебником математики сыт не будешь. Ведь если научить ребенка самостоятельно решать задачи в 1-3 классах, дальше он будет щелкать как семечки не только задачи по математике, но и по физике, химии, геометрии и др. И самое главное — этот навык пригодится ребенку в жизни!

vogazeta.ru

В статье Как научить ребенка математике мы подробно писали, из каких 4 частей состоит любая задача и что нужно сделать в первую очередь, чтобы ребенок понял, чего от него хотят и как ответить на вопрос задачи. Уяснив алгоритм решения задач, ребенок сможет самостоятельно решить практически любую задачу, даже несмотря на то, что они все кажутся такими разными.

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Основные типы задач по математике: краткий конспект

Небольшой ликбез, т.к. далеко не все родители учились в педагогических ВУЗах и владеют методикой преподавания. Пробежимся по теории, чтобы понимать, кто, кому и чего «должен». Зная ключевые моменты, вам будет проще помочь ребенку в решении задач, которые вызывают у него сложности, вы сможете определить, где пробелы в знаниях и что нужно «подтянуть» в каждом конкретном случае.

iqsha.ru

Рассмотрим самые распространенные виды задач в начальных классах.

Видео:РЕШЕНИЕ УРАВНЕНИЙ |ПОДРОБНОЕ ОБЪЯСНЕНИЕ КАК РЕШИТЬ УРАВНЕНИЯ / ПРОСТЫЕ УРАВНЕНИЯ 2 КЛАСС МАТЕМАТИКАСкачать

1. Простые задачи на сложение и вычитание

К этой группе относятся несколько задач, но для всех есть общие рекомендации:

• Решаются в одно действие.
• Иногда удобно составить уравнение.
• На их примере ребенок должен научится выполнять краткую запись.
• Если краткого условия недостаточно, нарисовать рисунок. Если не помог рисунок, показываем на конкретных предметах и производим действия с ними.
• Четко усвоить, что «+» — это прибавить, увеличить, а «-» — уменьшить, отнять, вычесть.
• Хорошо запомнить компоненты арифметических действий:

слагаемое + слагаемое = сумма
уменьшаемое — вычитаемое = разность

• Понять разницу между словами «стало» и «осталось». Четко понимать, что значит «на … меньше», «на … больше».

• Важно понять и запомнить: чтобы узнать, НА СКОЛЬКО одно число больше или меньше другого, нужно из большего числа вычесть меньшее.

• Важно понять и запомнить: чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

• Важно понять и запомнить: чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.

• Важно понять и запомнить: чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.

Задачи с косвенным вопросом

Это самые коварные задачи из этой группы. Внимательно прочитайте условие — и поймете почему.

На стоянке у первого подъезда 7 машин. Это на 2 машины больше, чем на стоянке у второго подъезда. сколько машин на стоянке у второго подъезда.

Видео:Математика 1 класс. Уравнения Решение уравнений вида а + х = bСкачать

2. Составные задачи на сложение и вычитание

Эти задачи решаются двумя и более действиями.

Есть несколько способов решения:

• по действиям с пояснениями;
• по действиям с вопросами;
• выражением.

В решении таких задач главное:

• найти главное и сделать краткую запись;
• разложить эту задачу на несколько простых и составить план решения;
• помнить главное: по двум данным находим третье.

Видео:3 класс. Математика. УравнениеСкачать

3. Задачи на понимание смысла действий умножения и деления

• Важно запомнить названия компонентов действий и понять их смысл:

1-й множитель х 2-й множитель = произведение
делимое : делитель =частное

• Ребенок должен понимать, что 1-й множитель показывает, КАКОЕ число повторяется а 2-й множитель показывает — СКОЛЬКО РАЗ оно повторяется.

Это очень важно для правильной записи в задачах, иначе получится бессмыслица.

Советы о том, как научить ребенка осознанно относиться к умножению и делению, вы найдете в нашей статье Как научить детей быстро считать: математика до школы. Если возникли проблемы с решением задач на умножение — сдайте чуть-чуть назад, закрепите осознание этого арифметического действия.

Видео:Простые уравнения. Как решать простые уравнения?Скачать

4. Простые задачи на умножение и деление

• Очень важно понять и запомнить разницу «в «, «на».

«Во сколько раз» или «на сколько»? Предлог «на» — это сложение или вычитание, а «в» — умножение или деление.

• Важно понять и запомнить: чтобы узнать, во сколько раз одно число больше или меньше другого, нужно большее число разделить на меньшее.

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

5. Составные задачи на все 4 арифметические действия

Видео:Как научить ребёнка решать уравнения без ошибокСкачать

6. Задачи на цену, количество, стоимость

Видео:Математика 2 класс (Урок№26 - Уравнение. Решение уравнений подбором неизвестного числа.)Скачать

7. Задачи на движение

Это отдельная обширная тема, вернемся к ней позже.

Видео:Решение уравнений | Математика 3 класс #4 | ИнфоурокСкачать

Типичные ошибки в решении задач

Ошибка №1. Ребенок невнимательно прочитал условие задачи.

Часто бывает так, что ошибки возникают от невнимательности. Так часто бывает в задачах с косвенным вопросом. Ребенок смотрит на цифры, вроде все логично, но… не верно.

Например: «У Маши 8 конфет, это на 2 меньше, чем у Кати. Сколько конфет у Кати».

Ребенок видит «на 2 меньше» и делает «логичный» вывод, что надо отнять. Отнять можно от бОльшего числа, т.е. сразу напрашивается решение 8-2=6. И ответ: 6 конфет у Кати. А ответ-то не тот! Если внимательно почитать условие, то станет понятно, что у Кати конфет больше чем у Маши. И вовсе тут не отнимать надо.

Как исправить ошибку. Сразу разберитесь с условием, поможет краткая запись.

Ошибка №2. Ребенок допустил ошибку в решении.

Когда в задаче несколько неизвестных, решение затрудняется, требуется выполнить не одно действие, а придумать целую цепочку рассуждений.

Как исправить ошибку. Для начала определим, каких данных нам не хватает. Решаем по действиям. Находим нужные числа (помним правило: по двум неизвестным находим третье), подставляем их и отвечаем на вопрос задачи.

Ошибка №3. Неправильная запись ответа.

Часто ребенок пишет не то пояснение.

Как исправить ошибку. Нужно внимательно прочитать вопрос задачи. Уяснить раз и навсегда, что ответ начинается с числа, а дальше пишем, что требовалось найти (переписываем формулировку вопроса задачи).

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Творческий подход в решении задач

www.craftykidsathome.com

• Учите ребенка рассуждать.
• Придумывайте задачи с лишними или недостающими данными.

Пусть ребенок сам вычеркнет лишнее, те данные, которые не влияют на решение.

• Дайте условие, а ребенок пусть сам придумает ответ.
• Пусть ребенок сам составит обратную задачу.
• Придумать несколько задач на одно решение.
• Придумать, как решить задачу другим способом и объяснить его.

Видео:Математика Петерсон 1 класс. Уравнения.Скачать

На школу надейся, а сам не плошай

Заглянем в педагогику и «расшифруем» мысли умных и заслуженных, исходя из сегодняшних реалий.

В далеком 1867 году К. Ушинский сказал: «У хороших преподавателей дело выходит так, что арифметическая задача есть вместе занимательный рассказ, урок сельского хозяйства или домашней экономии, или историческая или статистическая тема и упражнение в языке».

• Ученика нужно поставить в такие условия, чтобы он оказался в эпицентре событий, т.е., решая задачу, видел ее применение в жизни.

Не всегда задачи в школьном учебнике «вдохновляют» современных школьников. Многим не ясно условие по одной простой причине: ребенок не имеет представления о том, что говорится. Например, задача про надои и бидоны с молоком, а городской «деть» и корову-то в глаза не видел, не то, что тонны молока в бидонах. Или в задаче использованы такие значения, которые в жизни нереальны — это затрудняет восприятие, т.к. ребенок все воспринимает буквально.

Задача родителей — помочь ребенку ПОНЯТЬ условие. Любым способом: хоть рисуй, хоть танцуй.

• К решению задач нужно подходить творчески.

Интерес заставляет ребенка быть активным, а активность в свою очередь усиливает внимание.

В каждодневной жизни нам то и дело приходится решать задачи. Привлекайте ребенка, задавайте вопросы, просите совета. Например, тема ремонта. Вычислить метраж комнаты; просчитать нужное количество краски, зная расход на метр квадратный; купить линолеум, зная длину и ширину комнаты; просчитать, какой метраж выгоднее, если есть напольное покрытие шириной 2, 5 метра и 3 метра, чтобы меньше остатков было и по цене вышло выгоднее. Купить ткань на пошив постельного белья, зная размеры матраса. Примеров масса! И это работает гораздо эффективнее, чем «бездушная» задача в учебнике, которая совершенно не привязана к жизни и не вызывает эмоциональный отклик.

• При решении жизненных задач у ребенка помимо всего прочего развивается наблюдательность, речь, появляется рабочее настроение, развиваются творческие способности и самостоятельность.

Через некоторое время вы заметите, что ребенок различными способами комбинирует информацию, с легкостью составляет задачи сам, находя идеи в окружающем мире, а не высасывая из пальца.

• Когда ребенка просят составить собственную задачу, нужно следить и за содержанием, и за решением. Задача должна быть осмысленной и целесообразной.

Например, нельзя допускать таких «ляпов», как «Я съел 13 желтых груш и 20 зеленых яблок. Сколько фруктов я съел?» Задача теряет смысл, если она оторвана от жизни.

• От задачи надо идти к примеру, а не наоборот.

Дети мыслят не абстрактно, а конкретными образами. Пример 12-6 ни о чем не говорит, а вот ситуация, когда из 12 человек 6 уже купили билеты на футбольный матч — это совсем другое дело. Тут ребенок не задумываясь ответит, что оставшиеся шестеро очень рискуют, нужно поторопиться, иначе билетов может не хватить и придется сидеть у телевизора, вместо того, чтобы активно скандировать на трибунах в поддержку любимой команды.

Лебединцев в своей книге «Введение в современную методику математики» писал: «То влияние, которое может оказывать обучение счислению и вообще математике на умственное развитие детей, находится в прямой зависимости от материала, которым мы пользуемся при обучении; если в учебном материале будут преобладать отвлеченные упражнения в действиях и хитроумные задачи с условиями, лишенными внутренней связи и, по существу, далекими от жизни, то, упражняя учащихся на таком материале, мы, может быть, и выработаем у них формальные навыки в вычислениях и, пожалуй, изощрим их ум для разгадывания разных ребусов и головоломок, но отнюдь не сделаем их более способными к правильному мышлению в жизни или какой-либо области знания…».

Французский педагог Жан Мосе тоже был уверен, что «заставлять ребенка начинать с отвлеченного правила и затем предлагать ему задачи — это значит идти наперекор ходу развития человеческого ума…».

Видео:Уравнения для 2 класса Математика Как объяснить ребенку решение уравнений 2 классСкачать

Практические советы по решению задач от реальных мам

fb.ru

Что нам Ушинский, Лебединцев и Мосе, спросим у тех, кто «из нашей песочницы». Как они помогают своим детям решать задачи по математике, что «работает», какие приемы на практике доказали свою эффективность и помогли повысить успеваемость.

Татьяна, мама учеников 4 кл. и 6 кл.

«Я знаю, что особую сложность у детей вызывают задачи на скорость, поэтому начала готовить своих мальчишек к этому уже с 1 класса. Когда ехали к бабушке в Пинск, говорили о скорости, засекали время, считали сколько мы проехали км, смотрели на знаки и вычисляли сколько нам останется времени, если мы будем ехать с такой же скоростью и сколько, если папа будет ехать с другой. В общем, я очень удивлялась, когда мои пацаны на скорость задачи решали как орехи. Я поняла, что в моем детстве не хватало практического представления того, о чем говорилось в задачах».

Ольга, мама ученика 1 кл. и ученицы 4 кл.

«С задачами старшая плохо дружит)) Почти всегда приходит за помощью. Стараюсь выработать алгоритм решения, но частенько упираюсь в «лень подумать». Если совсем «затык», рисуем схемы. На дополнительные задачи совсем нет времени, а сама по своей воле заниматься ими дочь точно не будет)) Иногда встречаются задачи с некорректно поставленным вопросом, тут приходится помогать с формулировкой ответа.

Младшего усадить за математику очень сложно. В те редкие моменты, когда дело доходит до задач, он их решает в уме и выдает ответ устно).»

Вероника, мама учеников 2 кл. и 4 кл.

«Младший задачи решает без проблем, но ненавидит чертить схемы к ним и писать пояснения. Старший ходит на факультатив по математике, дома домашку сам делает».

Катерина, мама ученика 2 кл. и ученицы 5 кл.

«Сын отлично справляется сам. Он такие схемы рисует, что я иногда в шоке)). Если за помощью обращается дочь, стараюсь упростить условие задачи до понятных образов, а потом она сама догадывается, как сложную модель решить».

Татьяна, мама ученицы 5 кл.

«Чаще всего прибегаем к рисованию. Прямо вот как по условию… садимся и рисуем, как есть. Так сказать, наглядность помогает. Велосипедист выехал… значит рисуем человечка на велосипеде, город из которого он выехал и тд)))) Если катер плывет по течению, рисуем море, волны)))))) С пояснениями никогда исправлений со стороны учителя не было, да и у нас, собственно, тоже вопросов не возникало. Смотри по условию, что спрашивают — и пиши ответы возле каждого действия».

Наталья, мама ученика 5 кл.

«Приходилось объяснять дроби на примере сломанных карандашей, порванных в клочья бумажек. В гостях в тот момент был друг-проектировщик, он именно так решил наглядно пояснить сыну задачу. Я обычно прибегаю к помощи рисования. В задачах на скорость/время/расстояние рисовали целые истории: кто куда и на чем поехал, кого встретил по дороге и в какой момент. Порой решение задач превращалось в мультфильм, одного черновика обычно мало. Несколько раз решали задачи всей семьей: мама отдельно от папы, потом сравнивали результаты и каждый объяснял ребенку свой «самый рациональный и простой» способ. Как правило, у мужчин своя логика)), мое решение обычно отличается от папиного».

Уважаемые читатели! Делитесь в комментариях своими находками и сложностями в решении задач по математике с детьми. будем разы разобраться вместе и помочь советами и полезными статьями на интересующие вас темы.

Предлагаем Вашему вниманию программы развивающих занятий с собаками- терапевтами в зависимости от возраста ребёнка и Ваших пожеланий:

• Тренинг по освобождению от страха собак. 3+
• Занятия с собаками-терапевтами «Почитай собаке». 5+
• Занятие для малышей «Собаки-обнимаки». 0+ (до 3 лет)
• Обучающее занятие «Детям о профессиях людских и собачьих». 4+
• Обучающие занятия с собаками-терапевтами в рамках творческого лагеря. 8+
• Занятия с собаками-терапевтами и детьми с нарушениями в развитии. 5+
• Развивающий курс «Собака — друг человека». (4 занятия). 4+

Видео:Решение уравнений, 6 классСкачать

Решение уравнений в начальных классах

Ключевые слова: математика

«Овладение основами логического и алгоритмического мышления, пространственного воображения и математической речи, измерения, пересчета, прикидки и оценки, наглядного представления данных и процессов, записи и выполнения алгоритмов» — из ФГОС НОО Предметные результаты освоения основной образовательной программы начального общего образования.

Уже в начальной школе дети должны овладеть элементами логических действий (сравнения, классификации, обобщения, анализа и др.). Поэтому одной из важнейших задач, стоящих перед учителем начальных классов, является развитие основ логического мышления, которая позволила бы детям строить умозаключения, приводить доказательства, высказывания, логически связанные между собой, делать выводы, обосновывая свои суждения, и, в конечном итоге, самостоятельно приобретать знания. Математика именно тот предмет, где можно в большой степени это реализовывать.

В этой статье хочу рассмотреть уравнение как один из видов упражнений, направленных на развитие логического мышления, и использования алгоритмов при его решении.

Уравнения в начальных классах рассматриваются как верные равенства. Решение его сводится к отыскиванию того значения буквы (неизвестного числа), при котором данное выражение имеет указанное значение. Решить уравнение — значит найти число (значение переменной), при котором равенство будет верным.

В первую очередь, уравнения — очень мощный и наиболее универсальный инструмент для решения вычислительных задач. Самых разных.

1. В школе, как правило, работают с текстовыми задачами. Это задачи на движение, на работу, на проценты и многие-многие другие. Однако применение уравнений не ограничивается одними лишь школьными задачками.
2. Без умения составлять и решать уравнения не решить ни одной сколь-нибудь серьёзной научной задачи — физической, инженерной ли экономической. Например, рассчитать, куда попадёт ракета. Или ответить на вопрос, выдержит или не выдержит нагрузку какая-нибудь ответственная конструкция (лифт, мост…). Или спрогнозировать погоду, рост (или падение) цен или доходов.
3. В повседневной жизни без решения уравнений тоже не обойтись. Например, если вы строите дом, то вычисляете расстояния и углы. Если покупаете квартиру в ипотеку, подсчитываете размер кредита так, чтобы он вписался в Ваш бюджет. Или выбрать самую выгодную банковскую карту, просчитать литры краски для ремонта, уложить асфальт… Чаще всего в повседневной жизни встречаются задачи оптимизации: проехать за минимальные время, получить наибольший доход от своих вложений, закупиться материалами по наименьшей цене и т.п.

В общем, уравнение — ключевая фигура в решении самых разнообразных вычислительных задач.

Во-вторых, знания, умения и навыки, приобретенные школьниками при решении уравнений в начальной школе, помогут им в изучении математических дисциплин в старших классах и будут способствовать скорейшему усвоению нового материала. Обучение решению уравнений способствует развитию мышления у школьников, которое так необходимо не только при изучении стереометрии и геометрии в целом, но и в обыденной жизни.

В-третьих, можно так же отметить, что обучение навыкам решения уравнений в начальной школе является своевременным и необходимым, так как именно в этом возрасте учащиеся лучше усваивают полученную от преподавателя информацию и с раннего возраста начинают понимать основные принципы и методики решения более сложных задач.

Методика изучения уравнений

I. Подготовительный

Изучать уравнения дети начинают уже с первого класса, используя в помощь различные фигуры или предметы.

Следующие действия, к которым переходят учащиеся, связаны с нахождением числа в «окошке».

1. Какие записи верны?

Как изменить результат, чтобы записи стали верными?

2. Почитай выражение: 15 — в. Найди значение выражения, если в = 3, 4, 10, 11, 16.

3. Среди чисел, записанных справа, подчеркните то число, при подстановке которого в окошко, получится верное равенство.

• 3+ ___ = 9 4, 5, 6, 7
• ___ — 2 = 4 1, 2, 3, 4, 5, 6

В процессе выполнения таких упражнений дети привыкают к мысли, что неизвестным может быть не только сумма или разность, но и одно из слагаемых/уменьшаемое/вычитаемое.

На этом этапе я объясняю детям, что такое часть и целое. Кстати эти понятия помогут в решении не только уравнений, но и задач. Давайте более подробно остановимся на том, как же объяснить ребёнку, что такое часть и целое. Нам важно чтобы ребёнок понимал часть не только как отдельный кусок чего-то целого, но и в значении множества и подмножества. Сами эти термины будут использоваться только в 4-5 классе, но осознать суть этих понятий вполне способен и первоклассник, если объяснять на конкретных, доступных примерах, используя действия с предметами.

Сделать это очень просто.

Например, положите перед ребёнком 4 кружка красного цвета и 3 кружка синего цвета. Кружки должны быть одинакового размера и отличаться только цветом. Это обязательное условие. Предметы должны отличаться только одним признаком. Спросите, как можно назвать все эти фигуры. Всё это кружки. Чем они отличаются? Разложи кружки на группы. Какие группы у тебя получились?

Все кружки — это целое. Целое можно разделить на части. На какие части ты разделил все кружки? (На красные кружки и синие кружки). Назови что здесь целое, а что часть — это главный вопрос упражнения.

Возьмите одинаковые по размеру кружки 3-х цветов и повторите упражнение. Затем возьмите кружки одного цвета двух или трёх размеров и повторите задание. Помните, что основная цель подобных упражнений — чёткое понимание ребёнком таких понятий как целое и части. Предметы для выполнения таких заданий должны быть самые разнообразные: пуговицы одинакового размера, но разные по цвету или по форме, причём, обязательно должны быть группы полностью одинаковых пуговиц. Чайные, десертные и столовые ложки, блюдца, тарелки и чашки — посуда и так далее. Попутно при выполнении этих упражнений закрепите классификацию предметов и повторите слова-обобщения и дифференциацию предметов (одежда и обувь, мебель и бытовые приборы, пассажирский и грузовой транспорт, овощи, фрукты и ягоды и т.д.).

Нужно будет научить ребёнка отвечать на вопросы:

1. Как, одним словом можно все эти предметы правильно назвать?
2. На какие части можно разделить эти предметы?
3. Как назовём целое? Как назовём часть? Или что здесь целое, а что часть?

Как только вы заметите, что ребёнок свободно различает и называет целое и части, начинайте при помощи тех же предметов складывать части и вычитать часть из целого. Теперь основной целью обучения является понимание, и запоминание двух основных правил, на основе которых можно решать любые задачи и уравнения на сложение и вычитание.

Следует объяснить и выучить формулу этих правил:

1. Чтобы найти целое необходимо все эти части сложить: Ц = Ч + Ч
2. Чтобы найти часть, нужно из целого вычесть другую (известную) часть Ч = Ц — Ч
3. Немного подробнее о том, как это сделать, объясню на примере с кружками красного и синего цвета. Назови что здесь целое, а что часть? Что нужно сделать, чтобы на столе остались только красные кружки? (Убрать синие кружки).

Запомни правило: Чтобы найти одну часть, нужно из целого вычесть другую (известную) часть. Что нужно сделать, чтобы на столе были все кружки? (Сложить вместе красные и синие кружки).

Запомни правило: Чтобы найти целое число, необходимо все части сложить.

Начиная с подготовительного этапа, я в своей работе использую алгоритмы решения уравнений. Алгоритм — это набор понятных и точных инструкций, описывающих порядок действий исполнителя для достижения результата. Алгоритм решения уравнений помогает учащимся быстро и правильно находить корень уравнения. Схематичные алгоритмы в Приложение 2.

II. Введение понятия «уравнение»

Знакомство с уравнением происходит при решении задачи с отвлеченными числами. Например, к неизвестному числу прибавили 3 и получили 8; найти неизвестное число. По данным задачи составляется пример с неизвестным числом ( ___ + 3 =8). Затем учитель поясняет, что в математике принято обозначать неизвестное число латинскими буквами (н-р, Х (икс)). Предлагается записать пример с заменой неизвестного буквой. Ставиться цель научиться решать такие примеры. Решение основывается на знании состава числа и использовании наглядных пособий (кружки к примеру). Аналогично еще несколько примеров. После чего учитель поясняет, что такие примеры называются уравнениями и, что найти неизвестное число — значит решить уравнение. Определение уравнения и корня уравнения не дается в начальных классах.

III. Формирование умения решать уравнения

Способы решения уравнений

1. Способ подбора. Подбирается подходящее значение неизвестного числа из заданных значений, либо произвольного множества чисел. При подстановке данного числа в уравнение, оно должно превращать его в верное равенство. При подборе необходимо обращать внимание на то, с какого числа целесообразно начинать подбор. Подбор неизвестного числа может осуществляться с использованием числового ряда, по таблице сложения, с опорой на состав числа, в том числе на десятичный.

Накопленный опыт у школьников при решении уравнений позволяет им сократить количество подборов, что способствует углублению осознанности.

Очевидно, что неизвестное м. принимать только нулевое значение.

Очевидно, что х = 1, поскольку 78-1-1=76. математических выражений: «Найди уравнение среди предложенных записей:

2. Способ, опирающийся на взаимосвязь компонентов действий. Используются правила взаимосвязи компонентов действий. Трудность использования данных правил заключается в том, что многие дети путают правила взаимосвязи компонентов действий и названия компонентов (необходимо знать 6 правил и название 10 компонентов).

9+х=14. Неизвестно слагаемое. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Значит х = 14-9, х=5.

7-х=2. Неизвестно вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Значит х=7-2, х=5.

Для решения уравнений данным способом в первое время в своей практике использую алгоритм-помощник для решения уравнений. (Приложение 1)

Особо хочется отметить пункт «проверка»:

1. подставь найденное значение неизвестного в уравнение.
2. вычисли значение левой части уравнения.
3. сравни значение левой и правой части уравнения.

При проверке уравнения следует показать учащимся, что результат, полученный в левой части уравнения, нужно сравнить со значением в правой части. Необходимо добиться осознанного выполнения проверки.

Для уравнений со скобками вида (6+х)-5=38 используется правило взаимосвязи компонентов действий. Левую часть уравнения рассматривают сначала как разность, считая выражение в скобках единым неизвестным компонентом. Этот единый неизвестный компонент — уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое и т.д.

Ряд альтернативных учебников математики для начальных классов практикуют знакомство детей с более сложными уравнениями (Аргинская, Петерсон), для решения которых правила взаимосвязи компонентов действий рекомендуется применять многократно.

IV. Формирование умения решать задачи с помощью уравнений

Процесс решения текстовой задачи с помощью уравнений состоит из следующих этапов:

1. Восприятие текста задачи и первичный анализ ее содержания.
2. Поиск решения:
   1. выделение неизвестных чисел;
   2. выбор неизвестного, которое целесообразно обозначить буквой;
   3. переформулировка текста задачи с принятыми обозначениями;
   4. запись полученного текста.
3. Составление уравнения, его решение, проверка, перевод найденного значения переменной на язык текста задачи.
4. Проверка решения задачи любым известным способом.
5. Формулирование ответа на вопрос задачи.

Общеобразовательная школа выступает в качестве того учреждения, которое самым непосредственным образом отвечает за качество человеческой истории.

Каждое поколение людей предъявляет свои требования к школе. Раньше первостепенной задачей считалось вооружение учащихся глубокими знаниями, умениями и навыками. Сегодня задачи общеобразовательной школы иные. Обучение в школе не столько вооружает знаниями, умениями, навыками. На первый план выходит формирование универсальных учебных действий, обеспечивающих школьникам умение учиться, способность в массе информации отобрать нужное, саморазвиваться и самосовершенствоваться. Используя алгоритм, дети легко определяются с выбором действия, чей компонент нужно найти. В процессе алгоритмического решения необходимо выбрать нужный алгоритм, что требует конкретных знаний, переноса знаний в новую ситуацию, что учит думать.

📸 Видео

МАТЕМАТИКА 2 КЛАСС: ВИДЕО УРОК 22 - РЕШЕНИЕ УРАВНЕНИЙ | ДИСТАНЦИОННОЕ ОБРАЗОВАНИЕСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Как решать уравнения в несколько действий? Как объяснить ребёнку решение таких уравнений?Скачать

Уравнение | Математика 2 класс #19 | ИнфоурокСкачать

Решение уравнений. Видеоурок 28. Математика 6 классСкачать

6 класс, 42 урок, Решение уравненийСкачать