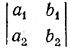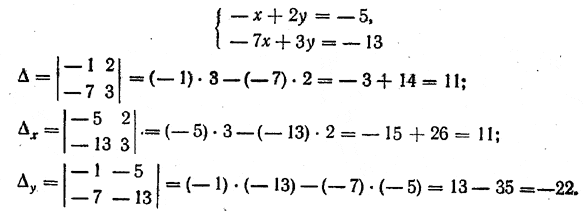Как найти вспомогательный определитель системы линейных уравнений (8 видео)

Содержание

Как найти вспомогательный определитель системы линейных уравнений
Вспомогательный определитель
Главная > Документ
Как найти вспомогательный определитель системы линейных уравнений
🌟 Видео

Видео:Решение системы уравнений методом Крамера.Скачать

Как найти вспомогательный определитель системы линейных уравнений

ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА I

§29 Главный и вспомогательный определители системы двух линейных ypaвнений с двумя неизвестными.

Главным определителем системы уравнений

(1)

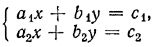
составленный из коэффициентов при неизвестных х и у. Этот определитель мы будем обозначать греческой буквой Δ (дельта). Очевидно, что

Первым вспомогательным определителем системы уравнений (1) называется определитель

Он получается из главного определителя этой системы уравнений путем замены первого столбца на столбец свободных членов. Этот определитель мы будем обозначать Δ_x. Индекс (то есть значок) х при Δ указывает, что в главном определителе Δ первый столбец, составленный из коэффициентов при х в системе уравнений (1), заменен на столбец свободных членов . Очевидно, что

Вторым вспомогательным определителем системы уравнений (1) называется определитель

‘

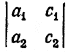
который получается из главного определителя этой системы путем замены второго столбца на столбец свободных членов. Этот определитель мы будем обозначать Δ_y. Очевидно, что

Пример. Для системы уравнений

Вопрос о том, какую пользу приносят введенные нами определители Δ , Δ_x и Δ_y при решении системы уравнений (1), мы выясним в следующих параграфах.

Найти главный и вспомогательные определители для следующих систем уравнений:

Видео:Решение системы уравнений методом Крамера 2x2Скачать

Вспомогательный определитель

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Системы линейных уравнений

Система уравнений следующего вида:

где а ij , b i – числовые коэффициенты, x i – переменные, называется системой линейных уравнений.

Решить систему линейных уравнений – значит указать все решения системы, то есть такие наборы значений переменных, которые обращают уравнения системы в тождества.

Система линейных уравнений называется:

совместной, если она имеет хотя бы одно решение;

несовместной, если она не имеет решений;

определенной, если она имеет единственное решение;

однородной, если все b i = 0;

неоднородной, если все b i ≠ 0.

(Габриель Крамер (1704-1752) швейцарский математик)

Данный метод применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.

Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.

Теорема. (Правило Крамера):

Система из n уравнений с n неизвестными

В случае, если определитель матрицы системы не равен нулю, то система имеет единственное решение и это решение находится по формулам:

х i = ;

где  — главный определитель , составленный из числовых коэффициентов при неизвестных, а  i – вспомогательный определитель , получаемый из главного заменой i -го столбца столбцом свободных членов b i .

 i =

Пример. Решить систему, используя правило Крамера.

;

 1 = ;  2 = ;  3 = ;

x 1 = ; x 2 = ; x 3 = ;

Пример. Найти решение системы уравнений:

 = = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

 1 = = (28 – 48) – (42 – 32) = -20 – 10 = -30.

x 1 = = 1;

 2 = = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.

x 2 = = 2;

 3 = = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.

x 3 = = 3.

Если система однородна, т.е. b i = 0, то при 0 система имеет единственное нулевое решение x 1 = x 2 = … = x n = 0.

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Этот метод удобен для решения систем невысокого порядка. Он основан на применении свойств умножения матриц.

Пусть дана система уравнений:

A = — матрица коэффициентов системы;

B = матрица – столбец свободных членов;

X = — матрица – столбец неизвестных.

Систему уравнений можно записать в матричной форме:

Сделаем следующее преобразование: A -1 AX = A -1 B,

т.к. А -1 А = Е, то ЕХ = А -1 В, получим

Х = А -1  В — решение матричного уравнения

Пример . Решить систему матричным методом

, , .

Получаем матричное уравнение .

Его решение , т.е.

(Нахождение обратной матрицы было рассмотрено ранее).

Ответ:

(Карл Фридрих Гаусс (1777-1855) немецкий математик)

В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

Рассмотрим систему линейных уравнений:

Определение: Матрица, составленная из коэффициентов при неизвестных системы, называется матрицей системы.

Определение: Матрица называется расширенной матрицей системы, если к матрице А присоединить столбец свободных членов системы.

Расширенная матрица – это закодированная запись системы. Строки матрицы соответствуют уравнениям системы. Умножение уравнения на число и сложение этого произведения с другим уравнением эквивалентно умножению строки матрицы на это число и почленному сложению произведения с другой строкой матрицы. Таким образом, работу с уравнениями можно заменить работой со строками матрицы.

Определение: Матрицу А называют ступенчатой, если:

А) любая ее строка имеет хотя бы один отличный от нуля элемент,

Б) первый отличный от нуля элемент каждой ее строки, начиная со второй, расположен правее неравного нулю элемента предыдущей строки.

Метод Гаусса является эффективным методом решения и исследования систем линейных уравнений. Он состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему ступенчатого вида, которая легко решается и исследуется. Применение метода Гаусса не зависит ни от числа уравнений, ни от числа неизвестных в системе.

Разберем идею метода Гаусса на конкретных примерах.

Пример. Решить систему линейных уравнений методом Гаусса.

Составим расширенную матрицу системы и с помощью элементарных преобразований приведем к виду:

Таким образом, исходная система может быть представлена в виде:

, откуда получаем: x 3 = 2; x 2 = 5; x 1 = 1.

Пример. Решить систему методом Гаусса.

Составим расширенную матрицу системы.

Таким образом, исходная система может быть представлена в виде:

, откуда получаем: z = 3; y = 2; x = 1.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Как найти вспомогательный определитель системы линейных уравнений

Дадим ряд необходимых определений.

Система линейных уравнений называется неоднородной, если хотя бы один ее свободный член отличен от нуля, и однородной, если все ее свободные члены равны нулю.

Решением системы уравнений называется упорядоченный набор чисел, который, будучи подставленным вместо переменных в систему, обращает каждое ее уравнение в тождество.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.

Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Рассмотрим неоднородную систему линейных алгебраических уравнений, имеющую при n = m следующий общий вид:

Главной матрицей A системы линейных алгебраических уравнений называется матрица, составленная из коэффициентов, стоящих при неизвестных:

Определитель главной матрицы системы называется главным определителем и обозначается ∆.

Вспомогательный определитель ∆ _i получается из главного определителя путем замены i -го столбца на столбец свободных членов .

Теорема 1.1 (теорема Крамера). Если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, вычисляемое по формулам:

Если главный определитель ∆=0, то система либо имеет бесконечное множество решений (при всех нулевых вспомогательных определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного из вспомогательных определителей).

В свете приведенных выше определений , теорема Крамера может быть сформулирована иначе: если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система является совместной определенной и при этом ; если главный определитель нулевой, то система является либо совместной неопределенной (при всех ∆ _i = 0), либо несовместной (при отличии хотя бы одного из ∆ _i от нуля).

После этого следует провести проверку полученного решения.

Пример 1.4. Решить систему методом Крамера

Решение. Так как главный определитель системы

отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители

Воспользуемся формулами Крамера (1.6):

Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.

Определить стоимость 1 единицы продукции молокоцеха каждого вида.

Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z – 1 кг творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из трех дней реализации можно отобразить следующей системой:

Решим систему методом Крамера. Найдем главный определитель системы по формуле (1.2):

Так как он отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители с помощью формулы (1.2):

По формулам Крамера (1.6) имеем:

Вернувшись к обозначениям, видим, что стоимость 1 литра молока равна 44 рубля, 1 кг масла – 540 рублей, 1 кг творога – 176 рублей

Примечание. Как видно, процесс вычисления определителей вручную с помощью калькулятора трудоемок, поэтому на практике используют персональный компьютер. Так, для решения систем линейных алгебраических уравнений методом Крамера в MS Excel высчитывают ее главный и вспомогательные определители с использованием функции МОПРЕД( ), где аргументом является диапазон ячеек и элементы матрицы, определитель которой находится.

В MathCAD для нахождения определителя пользуются палитрой оператора Matrix