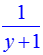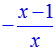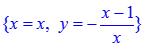Как найти все решения уравнения в maple (3 видео)

Как найти все решения уравнения в maple

* Entering and Manipulating Equations: The lhs and rhs commands *

Напомним, что уравнению, точно так же как и выражению, можно присвоить имя. В следующей командной строке мы введём уравнение и присвоим ему имя » eq1 » :

Мы можем вывести на экран левую и правую части уравнения по-отдельности при помощи команд lhs и rhs :

Воспользуемся командами lhs и rhs для того, чтобы привести уравнение к стандартному виду, в котором все члены собраны слева, а справа остался только 0:

Содержание

04. 02 Нахождение точных корней. Команда solve
Упражнение 4.1
04. 03 Поиск приближенных корней. Команда fsolve
Упражнение 4.2
Упражнение 4.3
Упражнение 4.4
Решение уравнений
Уравнения с одной переменной
Maple. Решение алгебраических задач. Решения уравнений, систем уравнений и неравенств в Maple
Страницы работы
Содержание работы
🔥 Видео

Видео:Решение системы линейных уравнений в MapleСкачать

04. 02 Нахождение точных корней. Команда solve

* Finding Exact Solutions: The solve command *

Рассмотрим вначале рациональные уравнения. Известно, что существуют алгоритмы определения точных корней рациональных корней вплоть до 4-го порядка включительно. В Maple-команду solve и заложены эти алгоритмы.

Воспользуемся командой solve для нахождения точных корней кубического уравнения :

Обратите внимание: в команде мы указываем, относительно какой переменной следует решать уравнение. Хотя в нашем конкретном случае это и не обязательно:

Maple нашел все 3 действительных корня и вывел их ( в неупорядоченном виде ).

Иногда очень важно выбрать конкретный корень, чтобы потом использовать в дальнейших преобразованиях именно его. Для этого заранее следует присвоить имя результату исполнения команды solve . Назовём его X . Тогда конструкция X[1] будет соответствовать первому корню из списка (подчеркнем: это не обязательно меньший корень! ), X[2] — второму корню, и т.д. ( Скобки — квадратные! ):

Посмотрите, однако, что будет выведено в результате выполнения похожей команды:

Ещё раз подчеркнём: практика показывает, что уравнению целесообразно присвоить имя. Традиционно в Maple такое имя начинается с букв eq :

(Не путать оператор присваивания » := » со знаком равенства » = » !)

Теперь решим уравнение при помощи команды solve . Множеству корней присвоим имя X :

Для убедительности проверим, нет ли среди найденных корней посторонних. Проверку выполним непосредственной подстановкой

Разумеется, частенько «точные» решения довольно громоздки, если не сказать иначе. Например, это касается уравнения :

Теперь Вам понятно, о чем речь? Для себя заметьте, что мнимая единица в Maple обозначается посредством прописной буквы I . Разумеется, в таких случаях не грех найти приближенные значения корней. Имея на руках точное решение, Вы и сами сообразите, как это сделать:

В подобных ситуациях хорошей альтернативой команде solve является fsolve , особенности которой будут рассмотрены в следующем параграфе.

Команда solve используется при отыскании точных решений не только рациональных уравнений. Ниже приведено несколько тому иллюстраций. Но для многих типов иррациональных, показательных, логарифмических, тригонометрических и даже рациональных уравнений точное решение искать бесполезно. На помощь призывается команда fsolve .

Решим уравнение :

Иногда (а в тригонометрии — всегда ) Maple, по умолчанию , не выводит всё множество корней:

Но безвыходных ситуаций не бывает! Взяв за основу полученный результат, воспользуйтесь своими знаниями тригонометрических уравнений и запишите полное решение ( как ? ).

Видео:Вычисления, константы и решение уравнений в MapleСкачать

Упражнение 4.1

Решить уравнение Разберитесь, сколько различных корней имеет уравнение. Как Maple поступает при наличии равных корней?

Совет : разложите на множители левую часть уравнения.

Корень х = 7 является двукратным, а потому у кубического уравнения только два различных корня. Разложение на множители левой части уравнения — тому подтверждение.

Видео:Графики, функции, решение системы линейных уравнений в MapleСкачать

04. 03 Поиск приближенных корней. Команда fsolve

* Finding Approximate Solutions: The fsolve command *

Для приближенного решения уравнений используется Maple-команда fsolve . В случае рационального уравнения, fsolve выводит весь список действительных корней (см. Пример 01). Для трансцендентных уравнений эта команда, по умолчанию, выводит только один корень (см. Примеры 02 и 03).

При помощи fsolve найдём приближенные значения сразу всех четырёх действительных корней рационального уравнения :

Эти четыре корня и составляют исчерпывающее решение исходного рационального уравнения ( хотя и приближенное ).

Используя команду fsolve , найти хотя бы один действительный корень уравнения :

Maple и вывел только один корень. На этот раз Maple не стал «живописать». Как теперь убедиться в том, что других действительных корней нет? Следующий пример даёт такой инструментарий.

Получить все действительные корни уравнения и убедиться в этом.

Шаг первый ( Основная идея ) : найдём графическое решение уравнения. Для этого построим график функции, стоящей в левой части уравнения. Абсциссы точек пересечения этого графика с осью Ох и будут искомыми корнями.

Т.к. мы умело подобрали диапазоны изменений абсцисс и ординат точек графика, то легко обнаружим 4 точки пересечения линии с осью Ох. Одна из них соответствует корню, найденному в Примере 02 ( какая именно? ).

Второй корень очевиден: х = 0. А как поточнее найти остальные?

Шаг второй ( Уточнение ) : применим команду fsolve более «зряче». В Maple предусмотрена возможность указания промежутка, на котором отыскиваются корни. В частности, для определения отрицательного корня нашего уравнения, укажем, что поиски следует вести в «районе» [-1;-0.2]. Об этом красноречиво свидетельствует графическое решение.

Оставшиеся корни явно принадлежат промежуткам [1;2] и [4;5] . Расскажем об этом команде fsolve :

Ну а что произойдёт, если мы подсунем Maple «пустой участок»? Например, отрезок [2;4] для нашего уравнения. Там графического решения явно нет:

Maple выдаёт название команды, само уравнение, имя аргумента и отрезок. Т.е. ничего нового. Мол: «Ищите корни сами, а я не нашел».

Шаг третий ( Дополнительный анализ ) : Как теперь удостовериться в том, что найдены все корни , а не только в видимой области графического решения? Для этого следует расширить интервал поисков:

Новых точек пересечения нет. В конце концов мы понимаем, что экспоненциальное слагаемое на границах промежутка вносит самый существенный вклад в величину функции из левой части уравнения. Значения функции в этой области стремятся к , а потому дополнительных корней нам не найти.

Попробуем в других местах: справа и слева от области найденных корней.

И здесь ни одного дополнительного корня! Поняв, что с влиянием показательной части уравнения всё ясно, делаем окончательные выводы.

Исчерпывающее решение уравнения состоит из четырёх корней: -.8251554597 , 0 , 1.545007279 , 4.567036837 .

Применим команду fsolve для приближенного решения трансцендентного уравнения .

Как и в предыдущем случае, найдём вначале качественное графическое решение. Для этого ещё нужно угадать, как разбросать по обеим частям уравнения его члены. Но графические возможности Maple настолько великолепны, что почти всегда можно собирать все члены уравнения с одной стороны.

Рассмотрим уравнение, равносильное данному: . Абсциссы точек пересечения графика функции, стоящей в левой части уравнения, с осью Ох и будут искомыми корнями.

График указывает область поисков корней: промежуток [1;2]. Настаёт черёд команды fsolve :

Корень найден. Но, очевидно, он — не единственный. Расширьте область поисков и ещё раз примените команду fsolve для отыскания второго корня.

Видео:РЕШЕНИЕ ВОЛНОВОГО ДУ ОПЕРАЦИОННЫМ МЕТОДОМ В СРЕДЕ MAPLESOFT MAPLE 2017Скачать

Упражнение 4.2

Найти все действительные корни уравнения , начав с графического решения.

Построим график левой части уравнения:

В результате находим корни уравнения в первом приближении: -2 ; -1.5 ; 0 . Применим теперь команду fsolve без указания диапазона поиска ( оценим возможности Maple ):

С удовлетворением отмечаем, что Maple выводит все три корня (Не будем забывать, что решали рациональное уравнение.)

Видео:Интерактивная математика в Maple 2017 | Clickable Math in Maple 2017Скачать

Упражнение 4.3

Найти все корни уравнения . Воспользуйтесь графическим решением. Проверьте каждый корень непосредственной подстановкой.

Приведём уравнение к стандартному (для этого раздела) виду:

Теперь построим график левой части уравнения:

По всей видимости, существует два корня. Один примерно равен -2, а другой, похоже, 2.

Применим команду fsolve , ограничив диапазон поиска:

Непосредственной подстановкой проверим корни:

Обратите внимание: в обоих случаях истинного равенства нет . С учётом ошибок при округлении, разумное расхождение вполне допустимо .

Убедитесь в отсутствии других корней. Ответ обоснуйте.

Видео:Начало работы с Maple 2017 | Getting Started with Maple 2017Скачать

Упражнение 4.4

Графики функций и дважды пересекаются на отрезке [-5;5].

а). Постройте в одной системе координат графики обеих функций и при помощи мыши найдите координаты точек пересечения.

b). Составьте уравнение, корнями которого являются абсциссы точек пересечения графиков.

c). Используйте команду fsolve для решения этого уравнения.

d). Используйте результаты из пункта с) для оценки ординат точек пересечения графиков.

e). У Вас не создалось впечатление, что линии могут пересекаться и в третьей точке с координатами (1;9)? Используйте fsolve и графические возможности Maple, чтобы убедиться в противном.

Видео:Maple Учимся рисовать в программеСкачать

Решение уравнений

Методы нахождения корней полиномов, решения уравнений, содержащих элементарные и специальные функции и систем сложных уравнений

Видео:Решение систем линейных уравнений в MapleСкачать

Уравнения с одной переменной

Для решения таких уравнений в Maple предусмотрены две команды: solve для символьного решения и fsolve для решения с ответом в численном виде. Например, формула для квадратного уравнения:

Синтаксис solve выглядит так: solve(equation,variable) . Параметры записаны через запятую. Если задать численные коэффициенты, то система попытается дать численные ответы:

Maple знает формулы для кубического уравнения:

но они сложны, неприятны по внешнему виду, и их почти никогда не применяют.

Используем численные коэффициенты, чтобы ответ был численным:

Этот результат – правильный, но поскольку Maple «думает» символами, то они не выглядят слишком пригодными. Для получения чисел с плавающей запятой следует применять уже известную команду evalf :

или вводить коэффициенты уравнения с десятичной точкой:

Команда solve с полиномами работает по-умному: она знает фундаментальную теорему алгебры о том, что полином n-го порядка имеет n корней. Например, если спросить о корнях уравнения x 6 + 1:

в ответе должны быть все шесть.

RootOf часто встречается при решении уравнений в Maple. В этой задаче задается полином с целыми коэффициентами, что для Maple означает попытку решить уравнение в радикалах (квадратных, кубических корнях и т. п.). Это создает проблему, и в результате он не может дать в решение ничего иного, кроме корня –1. Но если нужны только числа, либо используйте evalf , либо изменяйте коэффициенты на числа с плавающей точкой, и вы получите все шесть корней:

Maple может решать более сложные уравнения вроде cos(x) – x/10:

Снова RootOf , поэтому такой же подход к решению: чтобы получить хотя бы один корень, замените 10 на 10. или используйте evalf(s7)

При решении сложных уравнений надо проявлять осторожность, поскольку возможно более одного ответа, и Maple не даст все. Попробуем нарисовать функцию cos(x) – x/10 и увидим, как много у нее нулей, т. е. столько корней придется искать.

Maple на самом деле не обманывает: 1.427551779 есть решение, но не все.

Важно: прежде чем искать решение, постройте график, тогда будете знать, сколько корней надо найти.

Как заставить Maple выдать все корни? Поскольку они ищутся численно, применяется команда fsolve , которой надо задать уравнение, переменную и диапазон значений для поиска корней. Например, на рисунке видно, что корни находятся вблизи –9.6, –9.2, –4, –2, 1.5, 5 и 7. Это надо указать в fsolve , задавая диапазон поиска решений (x1..x2):

Посмотрите, что произойдет, если указать диапазон, где нет корней:

По общему правилу, когда Maple без вычислений возвращает то, что ему задали, это означает, что либо он не может найти ответ, либо вы ошиблись. Ищите, где ошибка.

Учтите, что вместо диапазона можно просто задать одно угаданное решение:

Здесь надо быть осторожным. Если для fsolve подсказано начальное значение, причем оно расположено близко к максимуму функции, нули которой ищутся, то fsolve может ошибиться или может найти решение не в том месте, где начальная подсказка. Посмотрим на примере метода секущих, почему так происходит:

Еще один способ контроля за решениями – опция avoid в fsolve .

Ищем решения уравнения cos(x) + x/3. Чтобы узнать, где искать корни, нарисуем функцию и увидим рядом с 3 два близко расположенных корня. Команда найдет один из них:

а вам нужен второй, и возникает проблема: как указать команде на него или как задать начальное значение. Можно так: ищи один корень вблизи 3, но не ищи s1:

Найдите все действительные или комплексные корни следующих полиномов. Используйте для этого команды solve и fsolve .

(a) x 4 – 1,

(b) x 3 + x 2 + x + 1.

solve дает комплексные величины, а fsolve – нет. Это можно исправить, указав fsolve , что нужно искать комплексные решения: fsolve(x^2+1=0, x,complex) .

Посмотрите, что случается при использовании команды factor(f,complex) , где f – полином, который надо разложить.

(a) Найдите все решения уравнения e x = 10sin(x) между –5 и 20.

(b) Найдите все решения уравнения e (–x) = x, используйте solve и fsolve и сравните ответы.

(с) Найдите все корни функции для x между 0 и 10.

(d) Найдите все корни производной функции Бесселя между 0 и 100 и занесите их в вектор-столбец a n .

Эту задачу можно решить очень компактно с помощью команды seq с командой fsolve внутри нее.

Решение разбейте на части:

Шаг 1. Нарисуйте функцию между 0 и 100, затем несколько раз обновите диапазон графика, чтобы узнать, где первый и второй корни и как далеко они друг от друга (вы обнаружите, что они на расстоянии порядка π).

Шаг 2. Чтобы применить полученную информацию, используйте команду seq , чтобы генерировать все корни.

Команда seq , вроде такой: seq(n^2,n=0..20) , генерирует список чисел; затем учтите, что первый аргумент seq , который генерирует зависящее от n число, может быть чем угодно, даже результатом fsolve .

Вот пример построения последовательности нулей косинуса с помощью seq и fsolve , который основан на догадке, что начинать надо с 1.4 и расстояние между нулями π: seq(fsolve(cos(x)=0,x=1.4+n*Pi),n=0..20);

Шаг 3. Все, что вам теперь нужно сделать, – загрузить эти числа в вектор-столбец. Если команда seq не дала первый корень при x=0 , догадайтесь, как это сделать вручную.

Видео:Решение уравнений в разных программахСкачать

Maple. Решение алгебраических задач. Решения уравнений, систем уравнений и неравенств в Maple

Страницы работы

Содержание работы

Решение алгебраических задач

Решение уравнений (часть 1)

Для решения уравнений, систем уравнений и неравенств в Maple используется команда (оператор) «solve». Например, для решения уравнения х2 – 6х + 5 = 0 набираем: > solve(x^2–6*x+5=0); 1, 5 Обратите внимание, что если аргумент solve не является уравнением (или неравенством), то Maple трактует его так, как если бы это выражение было приравнено к 0. Можно было бы написать «> solve(x^2–6*x+5);». При решении алгебраических уравнений Maple приводит все корни, включая комплексные: > solve(x^4=1); 1, –1, I, –I

Решение уравнений (часть 2)

С помощью команды «solve» можно решать не только алгебраические уравнения. Например, решим тригоно-метрическое уравнение tg x – 2 sin x = 0: > solve(tan(x)–2*sin(x)); Обратите внимание, что Maple привёл решения, лежащие в пределах одного промежутка периодичности (от –π до π). Для вывода всех решений необходимо присвоить зарезервированной переменной _EnvAllSolutions значение true: > _EnvAllSolutions := true; > solve(tan(x)–2*sin(x)); где _Z

обозначает любое целое число.

Решение уравнений (часть 3)

Приведём примеры применения функции «solve» для решения уравнений с несколькими переменными. Решим, например, уравнение xy + x – 1 = 0 относительно x: > solve(x*y+x–1,x); относительно y: > solve(x*y+x–1,у); В общем виде Maple решает это уравнение так: > solve(x*y+x–1); Видно, что форма ответа определяется вторым параметром (или его отсутствием) команды «solve», указывающим, относительно какой переменной решать уравнение.

Неравенства решаются тем же оператором «solve». Например, решим неравенство x2(x – 1) solve(x^2*(x–1) solve(x^2*(x–1)>=0); 0, RealRange(1, ∞) В переводе на математический язык ответ: U[1; ∞). Открытый интервал (или луч) задаётся в Maple с помощью функции «Open», применяемой к концам интервала, задаваемого функцией «RealRange».

Решение системы уравнений

Все уравнения системы записываются в фигурных скобках через запятую. Решим например систему > solve(); , Решим систему с параметром > solve(,);