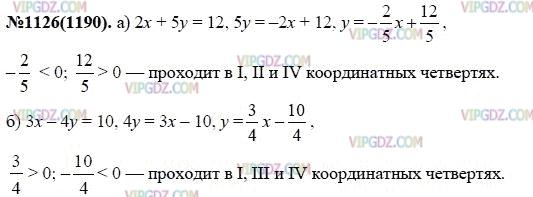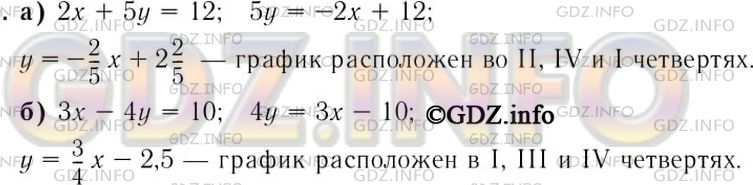Как найти в каких координатных четвертях расположен график уравнения

Условие

Решение 1

Решение 2

Поиск в решебнике

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Популярные решебники

Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013г.

Издатель: А.Г. Мордкович, 2013г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2015г.

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Алгебра. Урок 5. Графики функций

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Декартова система координат

• Функция

Видео:109 Алгебра 9 класс В каких координатных четвертях расположен график функции параболыСкачать

Декартова система координат

Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.

Координатные оси – прямые, образующие систему координат.

Ось абсцисс (ось x ) – горизонтальная ось.

Ось ординат (ось y ) – вертикальная ось.

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Функция

Функция – это отображение элементов множества X на множество Y . При этом каждому элементу x множества X соответствует одно единственное значение y множества Y .

Видео:Не выполняя построения, определите, где расположен график уравнения. №1053 алгебра 7 классСкачать

Прямая

Линейная функция – функция вида y = a x + b где a и b – любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :

Если a > 0 , прямая будет проходить через I и III координатные четверти.

b – точка пересечения прямой с осью y .

Если a 0 , прямая будет проходить через II и IV координатные четверти.

b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .

Важно : это уравнение не является функцией так как нарушается определение функции ( функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y ). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y . Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Видео:146 Алгебра 9 класс. Как расположен ГрафикСкачать

Парабола

Графиком функции y = a x 2 + b x + c является парабола .

Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :

1. Коэффициент a указывает на то, куда направлены ветки параболы.

• Если a > 0 , ветки параболы направлены вверх.
• Если a 0 , ветки параболы направлены вниз.

1. Коэффициент c указывает, в какой точке парабола пересекает ось y .
2. Коэффициент b помогает найти x в – координату вершины параболы.

1. Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .

• Если D > 0 – две точки пересечения.
• Если D = 0 – одна точка пересечения.
• Если D 0 – нет точек пересечения.

Видео:№ 109 - Алгебра 9 класс МакарычевСкачать

Гипербола

Графиком функции y = k x является гипербола .

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

На графике асимптоты отмечены зелёной пунктирной линией.

Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

0″ height=»346″ width=»346″ sizes=»(max-width: 346px) 100vw, 346px» data-srcset=»/wp-content/uploads/2017/01/Гипербола-1.png 346w,/wp-content/uploads/2017/01/Гипербола-1-150×150.png 150w,/wp-content/uploads/2017/01/Гипербола-1-300×300.png 300w,/wp-content/uploads/2017/01/Гипербола-1-176×176.png 176w,/wp-content/uploads/2017/01/Гипербола-1-60×60.png 60w, https://epmat.ru/wp-content/uploads/2017/01/Гипербола-1.png»>

Если k 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .

Видео:89 Алгебра 9 класс. В какой координатной четверти расположена точка пересечения графиковСкачать

Квадратный корень

Функция y = x имеет следующий график:

Видео:Алгебра 8 класс (Урок№14 - Функция y = k/x и её график.)Скачать

Возрастающие/убывающие функции

Функция y = f ( x ) возрастает на интервале , если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)

Примеры возрастающих функций:

Функция y = f ( x ) убывает на интервале , если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).

Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции , находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции , находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Видео:В какой четверти пересекаются графики. #ShortsСкачать

Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.

Видео:Занятие 1. График линейной функции y=kx+bСкачать

ГДЗ учебник по алгебрее 7 класс Макарычев. § 6. Контрольные вопросы и задания. Номер №7

В каких координатных четвертях расположен график функции:
y = 6 x;
y = 0,5 x + 4 ;
y = 3 x − 1 ;
y = − 3 ?

Видео:Функция у=к/х и её график. Алгебра, 8 классСкачать

ГДЗ учебник по алгебрее 7 класс Макарычев. § 6. Контрольные вопросы и задания. Номер №7

Решение

y = 6 x
k > 0 − график функции расположен в первой и третьей координатных четвертей.

y = 0,5 x + 4
k > 0 − график функции расположен в первой и третьей координатных четвертей.

y = 3 x − 1
k > 0 − график функции расположен в первой и третьей координатных четвертей.

y = − 3
k = 0 − график функции параллелен оси x и расположен в третьей и четвертых координатных четвертях.

🔍 Видео

Определение графика линейной функции по его формулеСкачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

ОГЭ 2022. Задание 11. Сопоставить функции и графики. Обратная пропорциональность. ГиперболаСкачать

Как построить график линейной функции.Скачать

Координатные четвертиСкачать

Как построить график функции без таблицыСкачать

Урок ГРАФИК ЛИНЕЙНОЙ ФУНКЦИИ 7 КЛАСССкачать

Функция. Область определения функции. Практическая часть. 10 класс.Скачать