3.7.2. Директрисы гиперболы

У гиперболы, как и у эллипса, две директрисы, и определяются они точно так же.

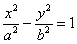
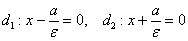
В каноническом положении директрисы расположены между ветвями гиперболы и задаются теми же уравнениями , где «эпсилон» – эксцентриситет данной гиперболы.

В нашей задаче:

Более того, для гиперболы справедлива абсолютно такая же теорема:

Гипербола – есть множество всех точек плоскости, таких, что отношение расстояния от каждой точки до фокуса к расстоянию от неё до соответствующей (ближайшей) директрисы равно эксцентриситету:

То есть, для любой точки гиперболы отношение её расстояния до фокуса к расстоянию от неё же до ближайшей директрисы равно эксцентриситету: . Для пары и любой точки гиперболы (ради разнообразия я выбрал демонстрационную точку дальней ветви) отношение такое же:

К слову, у параболы с её единственным фокусом и единственной директрисой по определению эти длины относятся «один к одному», поэтому эксцентриситет любой параболы и равен единице.

Ответ: искомая линия представляет собой гиперболу с центром симметрии в точке и повёрнутую на относительно своего канонического положения. Каноническое уравнение: , фокусы: , эксцентриситет: , асимптоты: , директрисы: .

Но я вас просто так не отпущу 🙂 – всё-таки разберу второй способ приведения линии к каноническому виду. Осуществим поворот системы на угол радиан против часовой стрелки и её параллельный перенос в точку . Тогда в системе уравнение примет вид: .

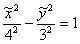
Чертёж будет выглядеть точно так же, как и чертежи выше – с той поправкой, что гиперболу мы изобразим в системе . Соответственно, все вычисления будут проводиться в новых координатах, и переменные следует записывать со значком «тильда»: . В частности, асимптоты запишутся так: , а директрисы – так: .

Очень хотелось упростить и даже вообще не рассматривать эту задачу, но она взята из конкретной контрольной работы, причём, заочного отделения. Поэтому пришлось с упорным занудством разобрать все-все-все тонкости и технические приёмы.

Налью вам стакан молока за вредность и предложу задачу для самостоятельного решения, она проще:)

Задача 110

Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки к расстоянию до прямой постоянно и равно . Сделать точный чертеж.

Подумайте, о какой это точке и о какой прямой шепчет условие 😉 Краткое решение и чертёж в конце книги.

И теперь вы готовы! (в хорошем смысле:))

– готовы рассмотреть суперзадачу, к которой я вас морально и технически готовил чуть ли не с первых параграфов темы.

…анекдот тут ещё вспомнился садистский про готовку, но, пожалуй, не буду – он неэтичный 🙂

Содержание

Гипербола и её свойства
Гипербола и её форма.
Урок 11
🔍 Видео

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Гипербола и её свойства

Видео:Видеоурок "Гипербола"Скачать

Гипербола и её форма.

Гиперболой мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac<x^><a^>-frac<y^><b^>=1.label
$$

Из этого уравнения видно, что для всех точек гиперболы (|x| geq a), то есть все точки гиперболы лежат вне вертикальной полосы ширины (2a) (рис. 8.6). Ось абсцисс канонической системы координат пересекает гиперболу в точках с координатами ((a, 0)) и ((-a, 0)), называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. Таким образом, гипербола состоит из двух не связанных между собой частей. Они называются ее ветвями. Числа (a) и (b) называются соответственно вещественной и мнимой полуосями гиперболы.

Рис. 8.6. Гипербола.

Для гиперболы оси канонической системы координат являются осями симметрии, а начало канонической системы — центром симметрии.

Доказательство аналогично доказательству соответствующего утверждения для эллипса.

Для исследования формы гиперболы найдем ее пересечение с произвольной прямой, проходящей через начало координат. Уравнение прямой возьмем в виде (y=kx), поскольку мы уже знаем, что прямая (x=0) не пересекает гиперболу. Абсциссы точек перечения находятся из уравнения
$$
frac<x^><a^>-frac<k^x^><b^>=1.
$$
Поэтому, если (b^-a^k^ > 0), то
$$
x=pm frac<sqrt<b^-a^k^>>.
$$
Это позволяет указать координаты точек пересечения ((ab/v, abk/v)) и ((-ab/v, -abk/v)), где обозначено (v=(b^-a^k^)^). В силу симметрии достаточно проследить за движением первой из точек при изменении (k) (рис. 8.7).

Рис. 8.7. Пересечение прямой и гиперболы.

Числитель дроби (ab/v) постоянен, а знаменатель принимает наибольшее значение при (k=0). Следовательно, наименьшую абсциссу имеет вершина ((a, 0)). С ростом (k) знаменатель убывает, и (x) растет, стремясь к бесконечности, когда (k) приближается к числу (b/a). Прямая (y=bx/a) с угловым коэффициентом (b/a) не пересекает гиперболу, и прямые с большими угловыми коэффициентами ее тем более не пересекают. Любая прямая с меньшим положительным угловым коэффициентом пересекает гиперболу.

Если мы будем поворачивать прямую от горизонтального положения по часовой стрелке, то (k) будет убывать, (k^) расти, и прямая будет пересекать гиперболу во все удаляющихся точках, пока не займет положения с угловым коэффициентом (-b/a).

К прямой (y=-bx/a) относится все, что было сказано о (y=bx/a): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из приведенных рассуждений вытекает, что гипербола имеет вид, изображенный на рис. 8.7.

Прямые с уравнениями (y=bx/a) и (y=-bx/a) в канонической системе координат называются асимптотами гиперболы.

Урок 11

Директрисы эллиПса и гиПерболы.

оПреДеление. Две Прямые, ПерПенДикулярные большой оси эллиПса и расПоложенные симметрично относительно центра на расстоянии а/e от него, называются Директрисами эллиПса (гДе а — большая Полуось эллиПса, e — эксцентриситет)

оПреДеление. Две Прямые, ПерПенДикулярные Действительной оси гиПерболы и расПоложенные симметрично относительно центра на расстоянии а/e от него, называются Директрисами гиПерболы (гДе а — Действительная Полуось, e — эксцентриситет)

уравнения Директрис эллиПса и гиПерболы имеют виД: х= ± а/e.

с Помощью Понятия Директрисы и эксцентриситета можно сформулировать общее свойство, Присущее эллиПсу и гиПерболе.

теорема. если r — расстояние от Произвольной точки м эллиПса (гиПерболы) До какого-нибуДь фокуса, d — расстояние от этой же точки До соответствующей этому фокусу Директрисы, то отношение r/d есть Постоянная величина, равная эксцентриситету эллиПса (гиПерболы).

Данное свойство можно Положить в основу общего оПреДеления этих линий: множество точек, Для которых отношение расстояний До фокуса и До соответствующей Директрисы является величиной Постоянной, равной e, есть эллиПс, если e 1.

возникает воПрос, что ПреДставляет собой множество точек, При условии e=1. оказывается, это новая линия второго ПоряДка, называемого Параболой.

оПреДеление. Параболой называется множество всех точек Плоскости, кажДая из которых нахоДится на оДинаковом расстоянии от Данной точки, называемой фокусом, и от Данной Прямой, называемой Директрисой и не ПрохоДящей через фокус.

Пусть м(х,у) — Произвольная точка Параболы. обозначим через r расстояние от точки м До фокуса f, через d — расстояние от точки м До Директрисы, а через P — расстояние от фокуса До Директрисы.

величину P называют Параметром Параболы. точка м лежит на Параболе, если r=P.

уравнение Параболы: у 2 =2Pх (каноническое уравнение).

исслеДуем форму Параболы По ее каноническому уравнению (Для не отрицательных значений у):

если х у 2 =2Pху 2 =-2Pхх 2 =2Pух 2 =-2Pу

Пример. Дано уравнение Параболы у 2 =6х. составьте уравнение ее Директрисы и найти коорДинаты фокуса.

решение. сравнивая Данное уравнение с каноническим уравнением Параболы, Получим, что 2р=6, откуДа р=3. так как фокус Параболы имеет коорДинаты (р/2;0), а Директриса — уравнение х=-р/2, то Для Данной Параболы Получаем: коорДинаты фокуса (1,5; 0) и уравнение Директрисы х=-1,5.

уПражнения .

составьте уравнение Параболы с вершиной в начале коорДинат и уравнение Директрисы Параболы, если известно, что осью симметрии является ось ох и что точка Пересечения Прямых у=х и у=2-х лежит на Параболе. (ответ: у 2 =х и х=-0,25)
Даны точки а(-1;0) и в(2;0). точка м(х;у) Движется так, что в треугольнике амв угол авм остается вДвое больше угла мав. оПреДелить траекторию точки м. (ответ: гиПербола)
Доказать, что если оси Двух Парабол взаимно ПерПенДикулярны и Параболы Пересекаются в четырех точках, то эти точки Пересечения лежат на оДной окружности.

Автор: Вяликова Мария Владимировна — учитель математики и информатики высшей квалификационной категории МАОУ Пролетарская СОШ Новгородского района Новгородской области