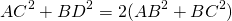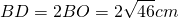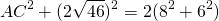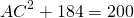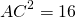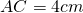Найти сторону треугольника через медиану и стороны — задача, обратная нахождению медианы через стороны.
Решается она аналогично, то есть с помощью дополнительного построения и применения свойства диагоналей параллелограмма.
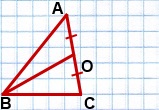
Стороны треугольника равны 6 см и 8 см. Медиана, проведенная к его третьей стороне, равна √46 см. Найти неизвестную сторону треугольника.
BO — медиана, BO=√46 см.
1) На луче BO отложим отрезок OD,
2) Соединим точку D с точками A и C.
3) AO=CO (так как BO — медиана по условию), OD=BO (по построению).
Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).
Если ввести обозначения BC=a, AB=c, AC=b, BO=mb, то получим формулу для нахождения стороны треугольника через медиану и две другие стороны:
Видео:Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать
Примеры решений по аналитической геометрии на плоскости
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.
Видео:Длина медианы треугольникаСкачать
Решения задач о треугольнике онлайн
Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.
Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.
Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.
Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.
Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.
Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.
Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$.
Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.
Видео:Уравнения стороны треугольника и медианыСкачать
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. 🎦 ВидеоКак построить треугольник 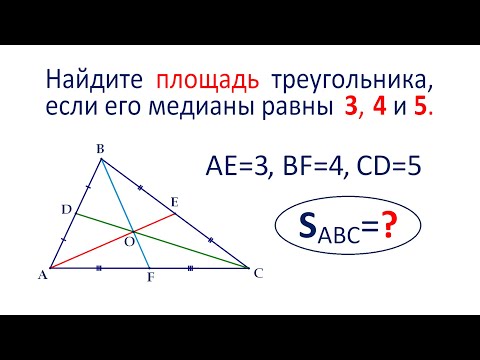по двум сторонам и медиане, проведенной к третьей сторонеСкачать  Формула нахождения медианы треугольника по известным сторонам треугольника.Скачать  Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать  Найдите сторону треугольника на рисункеСкачать  Найдите площадь треугольника, если его медианы равны 3, 4 и 5Скачать  №942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать  Вычисление медианы, высоты и угла по координатам вершинСкачать  Вычисляем высоту через координаты вершин 1Скачать  Найти площадь по двум сторонам и медианеСкачать  Треугольник с перпендикулярными медианами. Как найти третью сторону по известным двум?Скачать  7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать  №973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Найдите третью сторону треугольникаСкачать  Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать  найти уравнения биссектрис углов между прямымиСкачать  Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать  Геометрия 8 Класс Урок 4 Удвоение медианыСкачать  | ||