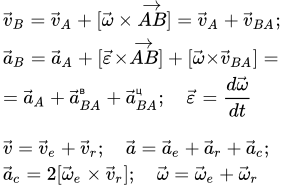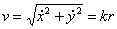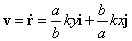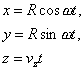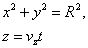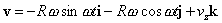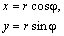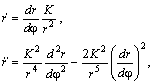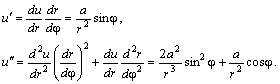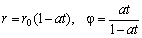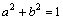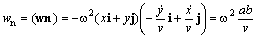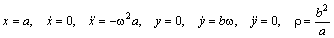- Скорость и ускорение точки в полярных координатах
- Траектория, скорость и ускорение точки при задании движения на плоскости в полярных координатах.
- Кинематика. Все определения, понятия, законы и теоремы
- Определение кинематики
- Кинематика точки
- Способы задания движения точки
- Векторный способ задания движения точки
- Координатный способ задания движения точки
- Естественный способ задания движения точки
- Скорость точки
- Скорость при естественном способе задания движения
- Ускорение точки
- Ускорение при естественном способе задания движения
- Скорость и ускорение точки в полярной системе координат
- Классификация движений точки
- Кинематика твердого тела
- Общие теоремы
- Поступательное движение
- Вращательное движение вокруг неподвижной оси
- Определение
- Угловая скорость и ускорение
- Частные случаи вращения тела
- Скорости и ускорения точек вращающегося тела
- Плоское движение твердого тела
- Определение скоростей
- Определение ускорений
- Мгновенный центр ускорений
- Сферическое движение твердого тела
- Свободное движение твердого тела
- Сложное движение точки
- Сложное движение твердого тела
- Сложение двух поступательных движений
- Сложение вращательных движений вокруг пересекающихся осей
- Сферическое движение
- Сложение вращений вокруг 2-х параллельных осей
- Направления вращений совпадают
- Вращения противоположны
- Пара вращений
- Сложение поступательного и вращательного движений
- Поступательное движение перпендикулярно оси вращения
- Винтовое движение
- Поступательное движение под произвольным углом к оси вращения
- Как найти уравнение траектории движения точки в полярной системе координат
- I Определение траектории, скорости и ускорения точки из закона движения в декартовых координатах.
- II . Движение в полярных координатах.
- III Проекция ускорения на естественные оси.
- 🔍 Видео
Видео:Полярная система координатСкачать

Скорость и ускорение точки в полярных координатах
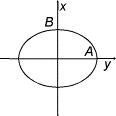
- Рассмотрим движение точек на плоскости. В этом случае движение может быть задано в полярных координатах. Для этого возьмите точку O на плоскости в качестве полюса и нарисуйте от нее полярную ось, например, ось быка (рис. 22). Если радиус-вектор r и полярный угол = f2 (t) — (23). Полярный угол считается положительным, если он простирается от полярной оси против часовой стрелки до радиус-вектора. Радиус-вектор как расстояние от точки О до точки М принимает только положительные значения.
Уравнение (23) называется уравнением движения для полярных точек. Это также параметрические точечные траекторные уравнения. Исключение параметра-времени t из (23) дает орбитальное уравнение в полярных координатах. F (r, r = rr °, gr = gfr °. Для проекции скорости на ось, положительное направление которой совпадает с направлением единичного вектора r ° и jr с (24), vr = r, gr = gf. (26) Их называют лучевой и боковой скоростями соответственно. В зависимости от знака производной мицелия лучевая и боковая скорости являются как положительными, так и отрицательными. Используйте (24), чтобы определить ускорение точки в полярных координатах. У нас есть a = dv / dl = (d / d /) (rr 0 + gfr °).
Потенциальная энергия N материальной точки в мыслимой точке силового поля M осуществляется силой поля, действующей на материальную точку при перемещении из точки M в начальную точку Mo, т. Людмила Фирмаль
Проведите дифференциацию и получите a = rf ° + r + r fr 0 + r fr 0 + r f. Для производной по времени единичного вектора p ° dp0 / d ^ = φ (-r0), Вектор p ° вращается с той же угловой скоростью φ, что и вектор r °, поэтому единичным вектором, на который направлен вектор dp ° / dt, является вектор (-r °). Ускоряя производную единичного вектора и подставляя ее в уравнение, объединяющее члены, получаем в = (r-rf2) r ° + (rf + 2rf) p °. (27) Получены точечные ускорения разложения на радиальные ар и боковые ап компоненты. a = a, + ap, ar = (r-rf2) r °, ar = (rf + 2rf) p °. Для проекции ускорений на оси Or и Op получаем a, = r-rp2, ap = rp + 2rp. (28).
Ускорение ar называется радиальным, поперечным направлением. Боковое ускорение также может быть выражено в следующем формате: Эта формула для бокового ускорения широко используется при рассмотрении движения планет и искусственных спутников Земли. Рисунок 23 Равные производные по Поскольку радиальная и боковая составляющие ускорения перпендикулярны друг другу, Для фиксированных координатных осей Ox, Oy и Oz формула ax = dvx / dt, ay = dvy / dt, a2 = dv: / dt. Для подвижных осей Or и Op, как видно из (26) и (28), a и ap не являются временами от vr и vp. Особый случай.
- В этих уравнениях φ — угловая скорость вращения радиус-вектора, а φ — его угловое ускорение. Пример 1. Движение точки — это уравнение r = / (l + COSOH), φ = ШГ, Где я и со постоянные значения. Определить скорость и ускорение точки в полярных координатах траектории уравнения, времени t и момента Решения. Из уравнения движения уберите следующее уравнение для орбиты в полярных координатах: r = f (1 + C0 $ f). Это кардиоидное уравнение (рис. 24).
Проекции скорости и ускорения на полярную ось определяются уравнениями (26) и (28). У нас есть: Мы получаем «, = / = — / Eosin South. 1> = Гф = / ш (1 + COSO) /), t> = + = к ^ 2 (1 + 008 J = ^ 39» 6,2 м / с Прогноз ускорения всегда определяется по формуле а = -2 м / с2; ау = -6 м / с2; а =. > / ai + a * = s / 40×6,3 м / с2, ускорение геля n -2coszsinz + 36-2sin2 (i Ускорение при 2 ^ / 16 cos2 / + 36 sin2 2 / — ^ / 3 / 5® — 0,3 м / с. Далее для r = n / 6 с Скорость предопределена Боковая скорость при =, л / 6 с — по формуле х = 4sin / | Координаты движущейся точки при t = n / 6 на / 6 / 6м. y = 3cos2r | / 6 = 1,5 м. Отметьте положение движущейся точки на траектории в соответствии с координатами, выберите масштаб и нарисуйте векторы скорости и ускорения из проекции на ось.
Таким образом, принцип возможного смещения не является в действительности активной силой, и помимо сил реакции идеального соотношения, для которых задача не определена, определяются все силы энергосистемы. Людмила Фирмаль
Для радиальной составляющей скорости в рассматривается направление, противоположное единичному вектору r °. Это потому, что v был найден со знаком минус. Только числовое значение определяется для боковой составляющей скорости. Из рисунка 25 видно, что направление вектора противоположно направлению единичного вектора p ° (направление p ° получается поворотом вектора r ° на 90 ° против часовой стрелки). Следовательно, в рассматриваемом случае вы должны использовать знак минус для vp, то есть c, = -b, 2 м / с.
Для проверки правильности определения vp вы можете использовать следующую формулу «F. Нормальное ускорение всегда направлено внутрь вогнутой поверхности дорожки. Оказывается, что направление тангенциального ускорения а определяется а и направлено вдоль вектора скорости. В результате точка в определенной точке ускоряется. Определить радиус кривизны орбиты в момент времени t = 1/6 с. Все необходимые для этого количества уже доступны. получить = — = 39/5 «7,8
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Траектория, скорость и ускорение точки при задании движения на плоскости в полярных координатах.
Если движение точки происходит в некоторой плоскости, то иногда целесообразно использовать полярную систему координат. Положение точки М в ней определяется координатами r и «фи», являющимися скалярными величинами.
Расположение полярной оси (луча, проведенного на плоскости из некоторой точки О) выбирают в плоскости движения точки, исходя из удобства решения задачи.
Полярный радиус r — скалярный неотрицательный параметр, равный длине отрезка ОМ, т.е. расстоянию от начала координат (точки О) до точки М.
Полярный угол «фи» — это угол между полярной осью и илнией ОМ (за положительное значение значение угла принимают направление, противоположное направлению движения часовой стрелки).
Для задания движения точки в полярной системе коодинат необходимо иметь уравнение движения в виде: 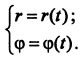
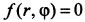
В полярной системе координат радиус-вектор точки, проведенный из центра О, равен 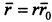
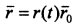
Вектор скоростипредставляется в виде суммы двух векторов, каждый из которых является составляющей скорости по направлению, задаваемому векторами r0 и p0 соответственно. Первое слагаемое называется радиальной составляющей, а второе — трансверсальной составляющей скорости точки: 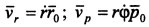
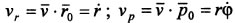
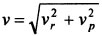
Ускорение точки: 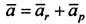
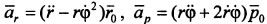
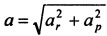
Дата добавления: 2018-11-26 ; просмотров: 1271 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Скорость и ускорение точки в полярных координатахСкачать

Кинематика. Все определения, понятия, законы и теоремы
Видео:Видеоурок "Полярная система координат"Скачать

Определение кинематики
Видео:Полярная система координатСкачать

Кинематика точки
Способы задания движения точки
Существуют следующие способы задания движения точки:
1) векторный; 2) координатный; 3) естественный.
Векторный способ задания движения точки
При векторном способе задания движения точки, положение точки определяется ее радиус-вектором , проведенным из некоторого центра O . При этом, радиус-вектор является функцией от времени t .
Радиус-вектор – это вектор, проведенный от предварительно выбранного центра O к материальной точке M :
.
Годограф вектора – это линия, которую вычерчивает конец вектора при его изменении во времени. При этом начало вектора находится в определенной точке пространства и его положение не меняется со временем.
Таким образом, траектория точки является годографом ее радиус-вектора.
Координатный способ задания движения точки
При координатном способе задания движения точки, мы выбираем систему координат. Обычно это прямоугольная система, но можно выбрать любую другую: цилиндрическую, сферическую и т. п. Тогда положение точки в пространстве определяется тремя координатами. В прямоугольной системе, их обозначают, как правило, буквами x, y, z. Зависимости этих координат от времени определяют закон движения точки:
.
Если движение происходит в одной плоскости, то мы выбираем систему координат в этой плоскости. В результате получаем два уравнения движения:
.
Исключив из этих уравнений параметр t , можно определить траекторию движения в виде функции , или .
При прямолинейном движении, выбрав ось x системы координат вдоль линии движения, имеем одну зависимость . Эта зависимость называется законом прямолинейного движения точки.
Связь между координатным и векторным способами задания движения точки
Пусть x, y, z – координаты точки в прямоугольной системе координат. Тогда
,
где – единичные векторы, проведенные в направлениях координатных осей;
– модуль вектора ;
– направляющие косинусы вектора . То есть это косинусы углов между вектором и осями координат.
Естественный способ задания движения точки
При естественном способе, система координат связана с траекторией движения точки. При этом мы считаем, что сама траектория нам известна. На этой траектории, мы выбираем положение неподвижного центра O . Тогда положение точки определяется длиной дуги s кривой, измеренной вдоль траектории от центра O до положения точки в момент времени t . Закон движения точки определяется как зависимость .
Дуговая координата s – это длина дуги траектории от некоторого неподвижного центра O до текущего положения точки. При этом в качестве центра O выбирается любая точка, принадлежащая траектории. Она является началом отсчета длины дуги s .
Переход от координатного способа к естественному выполняется по формулам:
;
.
Скорость точки
В прямоугольной системе координат, вектор скорости можно записать так:
.
Проекции скорости на оси координат (компоненты) равны производным координат по времени:
.
Модуль скорости: .
Направляющие косинусы: – это косинусы углов между вектором скорости и осями координат.
Равномерное движение точки – это движение, при котором модуль скорости остается постоянным.
Скорость при естественном способе задания движения
Вектор скорости направлен по касательной к траектории:
,
где – единичный вектор, направленный по касательной к траектории в сторону увеличения длины дуги s .
Абсолютная величина скорости равна абсолютной величине производной длины дуги траектории по времени:
.
Если , то движение происходит в сторону увеличения дуговой координаты s . Если , то дуговая координата уменьшается.
Удобно ввести алгебраическую величину скорости . Она равна проекции скорости на направление единичного вектора :
.
Это скалярная величина. В отличии от модуля скорости, она может иметь как положительное, так и отрицательное значение. Далее мы будем использовать следующие обозначения:
– это вектор скорости;
– его абсолютная величина;
– алгебраическая величина скорости – проекция скорости на направление вектора . При движение происходит в сторону увеличения дуговой координаты. При – в сторону уменьшения. Тогда
; .
Ускорение точки
Проекции ускорения на оси координат:
.
Модуль ускорения: .
Направляющие косинусы: .
Ускорение при естественном способе задания движения
При естественном способе задания движения, ускорение раскладывают на два взаимно перпендикулярных вектора: касательное (тангенциальное) к траектории, и нормальное (перпендикулярное) ускорение:
.
Модуль ускорения .
Касательное ускорение:
.
Здесь, как и для скорости, мы считаем, что – это скалярная величина, которая может принимать как положительные, так и отрицательные значения. Тогда
.
Продифференцировав модуль скорости по времени, получим:
.
Отсюда следует, что абсолютное значение производной модуля скорости по времени равно модулю касательного ускорения. Если угол между направлениями векторов ускорения и скорости острый, , то происходит увеличение скорости – ускоренное движение. Если угол тупой , то происходит уменьшение скорости – замедленное движение.
Нормальное ускорение перпендикулярно касательной к траектории и всегда направлено к центру кривизны:
.
Здесь – единичный вектор в направлении главной нормали траектории.
Пусть ρ – радиус кривизны траектории. Тогда модуль нормального ускорения
.
Вектор полного ускорения точки лежит в соприкасающейся плоскости к траектории. Поэтому его проекция на бинормаль равна нулю:
.
Скорость и ускорение точки в полярной системе координат
В полярной системе координат , положение точки M определяется по формулам:
.
Пусть – единичные векторы (орты), проведенные из точки M в сторону увеличения r и φ , соответственно. Тогда вектор скорости выражается через них по формуле:
.
Модуль скорости: ,
где – радиальная скорость; – поперечная скорость.
Ускорение точки
.
Радиальное ускорение: . Поперечное ускорение: . Модуль ускорения: .
Классификация движений точки
1) Прямолинейное равномерное движение.
. В этом случае скорость точки постоянна. Движение происходит по прямой, параллельной вектору скорости.
2) Криволинейное равномерное движение.
. Скорость точки постоянна по абсолютной величине, но движение происходит не по прямой, а по кривой.
3) Прямолинейное неравномерное движение.
. Скорость точки изменяется по абсолютной величине, но траектория прямолинейна.
4) Криволинейное неравномерное движение.
. Скорость точки меняется как по абсолютной величине, так и по направлению. Если направления векторов и совпадают, то это ускоренное движение. В противном случае – замедленное.
5) Равнопеременное криволинейное движение.
. Это частный случай криволинейного неравномерного движения. Здесь касательное ускорение постоянно. Алгебраическая величина скорости меняется по линейному закону: . Длина дуги траектории – по квадратичному: .
Видео:Построение кривой в полярной системе координатСкачать

Кинематика твердого тела
Общие теоремы
Расстояния между любыми двумя точками абсолютно твердого тела не меняется в процессе его движения. Эти связи приводят к дополнительным ограничениям на скорости движения точек. В результате получаются уравнения, связывающие скорости и ускорения точек. Такие уравнения носят название формул Эйлера.
Формулы Эйлера
Скорости и ускорения двух точек A и B твердого тела с радиус-векторами и связаны соотношениями:
(Т1) ;
(Т2) .
Здесь – некоторый аксиальный вектор, который называется угловой скоростью;
– вектор углового ускорения.
Доказательство.
Это фундаментальные уравнения. Точку A , при такой форме записи, называют полюсом. Тогда движение твердого тела можно рассматривать как поступательное движение полюса и вращательное движение относительно него.
Отметим еще одну теорему, которую часто применяют в расчетах.
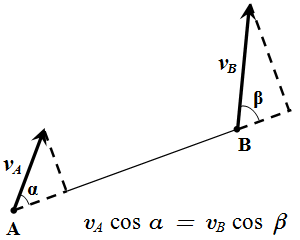
Теорема о проекциях скоростей двух точек твердого тела на прямую
Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу:
.
Доказательство.
Далее приводится классификация видов движения тела и применение формул Эйлера в конкретных случаях.
Поступательное движение
При поступательном движении все точки тела имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения, их траектории конгруэнтны, а разность радиус-векторов любых двух точек равна вектору, который зависит от положений сравниваемых точек, но не зависит от времени.
При поступательном движении угловая скорость и угловое ускорение равны нулю:
. Тогда формулы Эйлера ⇑ принимают вид:
.
Вращательное движение вокруг неподвижной оси
Определение
При вращении все точки тела движутся в плоскостях, перпендикулярных оси вращения. Их траекториями являются окружности с центром на оси вращения. Положение тела определяется углом поворота φ относительно произвольным образом выбранного нулевого положения. Зависимость угла поворота от времени определяет закон вращательного движения или, что тоже самое, уравнение вращательного движения. Единицей измерения угла поворота является радиан, который считается безразмерной величиной.
180° = π радиан ⇒ 1 радиан = 180/π = 57,29578°.
Угловая скорость и ускорение
Вектор угловой скорости параллелен оси вращения. Его направление определяется правилом правого винта. Он не имеет точки приложения и применим ко всем точкам твердого тела, то есть ко всему телу в целом. Однако, для наглядности, вектор угловой скорости изображают на оси вращения.
Единицей измерения угловой скорости является 1 рад/с или, что тоже самое, 1/с = с –1 . В технике встречаются другие единицы измерения. Пусть n – число оборотов в минуту. Тогда 1 оборот = 2π радиан ; 1 минута = 60 с ; ;
n об/мин = n·2π/60 рад/с. Тогда
.
Угловое ускорение – это производная угловой скорости по времени:
.
Единицей измерения углового ускорения является рад/с 2 или, что тоже самое, с –2 .
Вектор углового ускорения также параллелен оси вращения. При ускоренном вращении он совпадает с направлением угловой скорости. При замедленном – имеет противоположное направление.
Частные случаи вращения тела
Равномерное вращение. Угловая скорость постоянна; угловое ускорение равно нулю: .
Равнопеременное вращение. Угловая скорость линейно меняется со временем; угловое ускорение постоянно: .
Скорости и ускорения точек вращающегося тела
Скорости точек любого твердого тела связаны формулой Эйлера ⇑. Для тела, вращающегося вокруг неподвижной оси, в качестве полюса удобно выбрать любую точку на оси вращения. Тогда скорость точки с радиус-вектором тела, вращающегося с угловой скоростью , определяются по формуле:
.
Здесь – радиус-вектор произвольной точки на оси вращения. Если ось вращения проходит через начало координат, то в качестве можно выбрать точку начала координат . Тогда
.
По правилам векторного произведения,
.
Здесь |CM| – расстояние от точки M до оси вращения (см. рисунок ⇓). Точка M движется по окружности радиуса |CM|. Вектор скорости направлен по касательной к этой окружности в сторону, которая задается направлением вектора угловой скорости.
При вычислении векторного произведения, полезно использовать следующие формулы:
.
Здесь – проекции угловой скорости на оси координат. Таким образом, проекции вектора скорости точки определяются так:
.
Если ось вращения совпадает с осью z, то , .
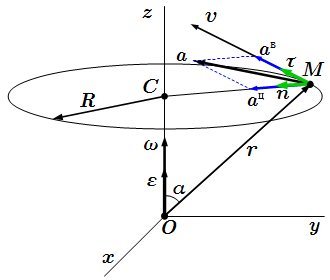
Скорость и ускорение точек твердого тела при вращении вокруг неподвижной оси Oz .
Ускорение точки определяется по формуле:
.
Вращательное ускорение:
;
.
Оно направлено по касательной к траектории и связано с изменением скорости точки по абсолютной величине.
Центростремительное (осестремительное) ускорение:
.
Оно направлено по главной нормали – к центру окружности и по абсолютной величине равно
,
где R – расстояние до оси вращения.
Модуль полного ускорения:
.
Угол β между векторами полного и центростремительного ускорений:
.
Плоское движение твердого тела
При плоском движении, все кинематические величины (перемещения, скорости и т.д.) имеют одинаковые значения для всех плоскостей, параллельных плоскости движения. Поэтому для описания плоского движения, нам достаточно рассмотреть движение любого сечения тела, или как говорят, плоской фигуры. Все результаты, полученные для одной плоской фигуры применимы и для других сечений, параллельных плоскости движения. Хотя плоская фигура имеет свои контуры и характерные точки, но мы считаем, что она не ограничена в размерах, поскольку ее размер может зависеть от выбора сечения. Кроме этого имеются некоторые точки, например мгновенный центр скоростей, которые служат только для проведения расчетов и могут находиться за пределами тела.
Для описания плоского движения, мы выбираем плоскую фигуру; проводим в ней двумерную систему координат x, y. Далее, произвольным образом выбираем точку A . Эту точку мы будем называть полюсом. Тогда положение тела однозначно определяется координатами точки A и углом поворота φ , относительно, произвольным образом выбранного направления, например оси x . При этом движение тела определяется тремя уравнениями, которые называют уравнениями плоского (или плоскопараллельного) движения тела:
.
Эти уравнения также называют уравнениями движения плоской фигуры. При таком описании, движение тела слагается из поступательного движения полюса A , и вращательного движения вокруг него. Поступательное движение зависит от выбора полюса, а угол поворота φ – нет.
Определение скоростей
Скорость точки B с радиус-вектором определяется по формуле Эйлера ⇑:
(П1) .
То есть скорость точки B тела равна векторной сумме скорости полюса A и относительной скорости . Относительное движение является вращением с угловой скоростью относительно оси, проходящей через полюс A перпендикулярно плоскости фигуры. Поскольку вектор угловой скорости перпендикулярен плоскости движения, то он перпендикулярен и вектору скорости. Тогда модуль относительной скорости равен произведению угловой скорости на расстояние от точки до полюса:
.
Мгновенный центр скоростей
Определения и свойства
Далее мы будем обозначать мгновенный центр скоростей буквой P . Для плоской фигуры – это точка. Для твердого тела – это ось, проходящая через точку P перпендикулярно плоскости движения. Эта ось может находиться за пределами тела.
Если плоская фигура движется непоступательно, то мгновенный центр скоростей всегда существует. Для поступательного движения, МЦС находится на бесконечности.
Приняв МЦС P в качестве полюса, получим значение вектора скорости произвольной точки B :
.
Поскольку движение плоское, то . Тогда модуль скорости точки B плоской фигуры равен произведению угловой скорости на расстояние до мгновенного центра скоростей:
.
Вектор скорости перпендикулярен отрезку, соединяющим точку с МЦС и направлен в сторону вращения плоской фигуры.
Скорости точек плоской фигуры пропорциональны их расстояниям до МЦС:
(Ц1) .
Модуль угловой скорости плоской фигуры равен отношению модуля скорости произвольной точки к ее расстоянию до мгновенного центра скоростей:
.
Теорема Шаля
Плоскую фигуру можно переместить из одного положения в любое другое положение одним поворотом этой фигуры вокруг некоторого неподвижного центра, который называют центром вращений, или осью вращений.
Мгновенный центр вращений – это центр вращений, определяемый согласно теореме Шаля, при бесконечно малом перемещении фигуры.
Если рассматривать перемещение плоской фигуры со временем, то мгновенный центр вращений совпадает с мгновенным центром скоростей.
Неподвижная центроида – это геометрическое место мгновенных центров скоростей, отмеченных на неподвижной плоскости.
Подвижная центроида – это геометрическое место мгновенных центров скоростей, отмеченных на плоской фигуре.
Например, если колесо катится без проскальзывания по неподвижной прямой, то неподвижной центроидой является прямая, а подвижной – обод колеса.
Теорема Пуансо
При движении плоской фигуры, подвижная центроида катится без скольжения по неподвижной центроиде.
Определение положения МЦС
1) Если скорости и точек A и B не параллельны, то МЦС есть точка пересечения прямых, проведенных через эти точки, перпендикулярно векторам их скоростей.
2) Если векторы и не равны, параллельны и перпендикулярны прямой AB , то для определения МЦС необходимо знать модули и направления скоростей, и применить формулу (Ц1).
3) Если векторы и равны, то МЦС находится на бесконечности, .
4) Если тело катится без скольжения по неподвижной поверхности, то МЦС находится в точке соприкосновения тела и поверхности.
Определение ускорений
Дифференцируя уравнение Эйлера (П1) по времени, получаем ускорение точки B :
(П1) ;
.
Итак мы нашли ускорение произвольной точки B плоской фигуры. Этот результат можно представить в следующем виде:
.
То есть ускорение произвольной точки B плоской фигуры равно геометрической сумме ускорения полюса и ускорению этой точки относительно полюса , которое определяется по формулам вращательного движения относительно неподвижного центра A . То есть равно геометрической сумме вращательного и центростремительного ускорений:
.
Вращательное ускорение относительно полюса перпендикулярно отрезку AB , соединяющим точку с полюсом. Центростремительное относительное ускорение направлено от точки B к A . Поскольку угловое ускорение также перпендикулярно AB , то
.
Мгновенный центр ускорений
Чтобы построить точку Q нужно выполнить следующие действия.
1) Из полюса A построить вектор ускорения .
2) Из полюса A провести луч AQ под углом к вектору ускорения полюса так, чтобы направление поворота от к AQ совпадало с направлением углового ускорения ε .
3) На луче AQ построить точку Q на расстоянии от точки A .
Приняв точку Q в качестве полюса, получим ускорение произвольной точки B твердого тела:
,
где – единичный вектор касательной к окружности радиуса QB ; – единичный вектор, направленный от B к Q .
Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгновенного центра ускорений:
.
Векторы ускорений составляют с отрезками, соединяющими эти точки и мгновенный центр ускорений один и тот же угол
.
Мгновенный центр скоростей P и мгновенный центр ускорений Q являются различными точками плоской фигуры.
Сферическое движение твердого тела
При сферическом движении, точки тела движутся по сферическим поверхностям. Положение тела часто определяют с помощью трех углов ψ, θ, φ , которые называются углами Эйлера. Для этого вводят две системы координат – неподвижную , и подвижную Oxyz , связанную с телом. Связь между ними осуществляется следующим образом.
1) Поворачиваем неподвижную систему координат на угол ψ вокруг оси . Получаем систему .
2) Поворачиваем систему координат на угол θ вокруг оси ON . Получаем систему ONK′z .
3) Поворачиваем систему координат ONK′z на угол φ вокруг оси Oz . Получаем систему координат Oxyz , связанную с телом.
Ось ON называется линией узлов; ψ – угол прецессии; θ – угол нутации; φ – угол собственного вращения. При движении тела, эти углы являются функциями от времени:
.
Теорема Эйлера – Даламбера
Твердое тело, имеющее одну неподвижную точку, можно переместить из одного положения в любое другое поворотом вокруг некоторой оси, проходящей через неподвижную точку.
Следствие теоремы Эйлера – Даламбера
При сферическом движении твердого тела существует ось, на которой скорости точек равны нулю. Такая ось называется мгновенной осью вращения.
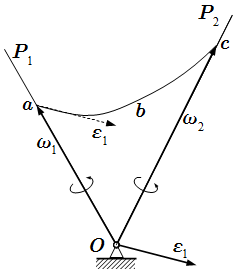
Угловое ускорение ε является касательной к годографу abc угловой скорости. P1, P2 – мгновенные оси вращения.
Угловая скорость тела параллельна мгновенной оси вращения. Для удобства ее вектор откладывают из неподвижной точки. При движении, угловая скорость изменяется как по абсолютной величине, так и по направлению. Конец вектора описывает годограф вектора угловой скорости.
Угловое ускорение – это скорость изменения угловой скорости:
.
Оно направлено по касательной к годографу вектора угловой скорости. При сферическом движении, в отличии от случаев вращения вокруг неподвижной оси и плоского движения, направление вектора углового ускорения может не совпадать с направлением вектора угловой скорости.
Скорости точек тела определяются по формуле Эйлера ⇑. В качестве полюса возьмем неподвижную точку O . Тогда для скорости произвольной точки с радиус-вектором имеем: . Если начало координат выбрать в точке O , то , тогда
.
Модуль скорости определяется по формуле:
,
где α – угол между векторами и ; h – расстояние от точки до мгновенной оси вращения.
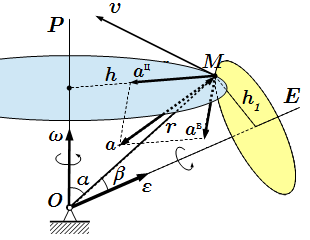
Ускорение при сферическом движении твердого тела.
Ускорение точки определяется по формуле:
.
Вращательное ускорение направлено перпендикулярно плоскости, образованной векторами углового ускорения и радиус-вектором . Оно имеет модуль , где β – угол между векторами и ; – расстояние от точки до оси E, проведенной из неподвижного центра O параллельно вектору углового ускорения.
Центростремительное (осестремительное) ускорение направлено к мгновенной оси вращения P и перпендикулярно ей. По модулю оно равно .
Свободное движение твердого тела
Это самый общий случай движения твердого тела. Свободное тело имеет шесть степеней свободы. Для описания его движения, выберем произвольную точку A тела в качестве полюса. Далее вводим две системы координат – неподвижную OXYZ, и подвижную систему , начало которой в каждый момент времени совпадает с точкой A, а оси параллельны осям неподвижной системы OXYZ. Таким образом, система совершает поступательное движение относительно OXYZ. Тогда свободное движение твердого тела можно рассматривать как сложное движение, состоящее из поступательного движения по закону движения полюса A, и сферического движения в системе координат , с неподвижной точкой A.
Уравнения движения свободного твердого тела представляют собой шесть равенств:
.
Здесь ψ, θ, ϕ – углы Эйлера. Первые три уравнения определяют поступательную часть движения и зависят от выбора полюса. Последние три уравнения определяют сферическое движение, и от выбора полюса не зависят.
Скорость любой точки B тела равна векторной сумме скорости полюса и скорости этой точки при ее сферическом движении относительно полюса:
,
где – радиус-вектор, проведенный из точки A в точку B.
Ускорение точки свободного твердого тела равно векторной сумме ускорения полюса, центростремительного (осестремительного) ускорения точки и ее вращательного ускорения относительно полюса:
.
Видео:7.9. Задание движения точки в полярных координатахСкачать

Сложное движение точки
Для описания сложного движения, мы выбираем неподвижную (основную) систему координат и подвижную . Будем считать, что подвижная система связана с некоторым движущимся твердым телом, относительно которого, в свою очередь движется точка. Например, человек, идущий в движущемся вагоне. Здесь неподвижная система координат – это система, связанная с рельсами и ландшафтом. Твердое тело – вагон. Точка – человек. Подвижная система координат – система, связанная с вагоном. Абсолютное движение – движение человека относительно рельс; относительное движение – движение человека относительно вагона; переносное движение – движение вагона относительно рельс.
Абсолютная скорость (ускорение) точки – это скорость (ускорение) точки в неподвижной системе координат.
Переносная скорость (ускорение) точки – это скорость (ускорение) той точки подвижной системы координат, в которой, в данный момент времени, находится точка, совершающая сложное движение.
Относительная скорость (ускорение) точки – это скорость (ускорение) точки относительно подвижной системы координат.
Теорема о сложении скоростей
При составном движении абсолютная скорость точки равна векторной сумме переносной и относительной скоростей:
.
Модуль абсолютной скорости: .
Эту теорему также называют правилом параллелограмма или треугольника скоростей.
Теорема Кориолиса о сложении ускорений
При составном движении, абсолютное ускорение точки равно векторной сумме переносного , относительного и кориолисова (поворотного) ускорений:
,
где – ускорение Кориолиса (кориолисово ускорение); – угловая скорость вращения подвижной системы координат.
Кориолисово ускорение также называют поворотным ускорением. Оно характеризует изменение направления относительной скорости точки, вызванное вращением подвижной системы координат. Если переносное движение является поступательным, то , кориолисово ускорение равно нулю.
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Сложное движение твердого тела
Теперь рассмотрим сложное движение твердого тела – то есть такое движение, при котором твердое тело движется относительно некоторой системы координат , которая, в свою очередь движется относительно неподвижной системы координат . Такое движение часто называют сложением движений. Пусть A – произвольная точка тела, которую мы выберем в качестве полюса. Тогда скорость произвольной точки B тела относительно подвижной системы координат определяется по формуле:
.
В свою очередь, подвижную систему координат также можно рассматривать как твердое тело. Тогда скорость точки B при переносном движении:
.
Применяя теорему о сложении скоростей, найдем скорость точки B относительно неподвижной системы отсчета:
.
Отсюда следует, что скорость полюса относительно неподвижной системы координат равна векторной сумме скоростей полюса при переносном и относительном движениях:
.
Угловая скорость равна векторной сумме угловых скоростей:
.
Рассмотрим частные случаи сложного движения твердого тела.
Сложение двух поступательных движений
При сложении двух поступательных движений, . Тогда . Результирующее движение также является поступательным. Скорость результирующего движения равна сумме скоростей составляющих движений:
.
Сложение вращательных движений вокруг пересекающихся осей
При сложении двух вращательных движений вокруг пересекающихся осей, результирующее движение также является вращательным. При этом ось вращения проходит через точку пересечения осей параллельно вектору абсолютной угловой скорости:
.
Если оси вращения изменяются со временем, то все сказанное выше имеет место для мгновенных осей вращения.
Аналогично предыдущему, при сложении нескольких вращательных движений вокруг пересекающихся осей, результирующее движение также является вращательным. Ось результирующего вращения проходит через точку пересечения осей параллельно вектору абсолютной угловой скорости:
.
Сферическое движение
Как было указано ранее, при сферическом движении, положение тела можно задать с помощью углов Эйлера. Они определяются последовательными переходами от неподвижной системы координат к системе координат , связанной с телом: . Такие переходы можно рассматривать как сложное движение, состоящее из серии вращений ⇑. При этом каждая последующая система координат является повернутой относительно предыдущей на соответствующий угол: ψ, θ, φ , изменяющиеся со временем. Дифференцируя эти углы по времени, получаем угловые скорости вращений систем координат, которые имеют следующие названия:
– угловая скорость прецессии; – угловая скорость нутации; – угловая скорость собственного вращения.
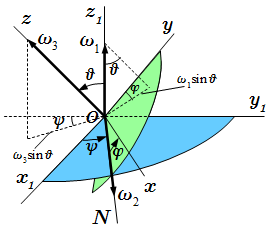
Связь угловых скоростей с углами Эйлера.
Векторы этих угловых скоростей направлены, соответственно, вдоль осей . Тогда вектор угловой скорости тела относительно неподвижной системы координат равен сумме угловых скоростей:
.
Его модуль:
.
Проекции вектора угловой скорости на оси подвижной системы координат Oxyz определяются с помощью кинематических уравнений Эйлера, которые имеют следующий вид:
;
;
.
Сложение вращений вокруг 2-х параллельных осей
Направления вращений совпадают
Если направления вращений совпадают, то угловая скорость, при абсолютном движении, равна сумме модулей угловых скоростей переносного и относительного движений: . Направление вектора совпадает с направлениями векторов и . Движение является плоскопараллельным. Мгновенная ось вращений проходит через точку C (см. рисунок), находящуюся между осями вращений. При этом
;
.
Вращения противоположны
В этом случае, угловая скорость, при абсолютном движении, равна модулю разности абсолютных значений угловых скоростей: , а направление совпадает с направлением наибольшей по абсолютной величине угловой скорости. Движение также является плоскопараллельным. Мгновенная ось вращений проходит через точку C (см. рисунок) так, что ось с наибольшей угловой скоростью оказывается между остальными осями. При этом
;
.
Пара вращений
Пара вращений – это такое сложное движение твердого тела, при котором угловые скорости противоположны по направлению и равны их абсолютные значения: . В этом случае тело совершает поступательное (или мгновенное поступательное движение). Скорости всех точек тела равны . Мгновенная ось вращения находится на бесконечности. Примером такого движения является движение педалей велосипеда относительно рамы.
Сложение поступательного и вращательного движений
Поступательное движение перпендикулярно оси вращения
Если скорость поступательного движения перпендикулярна оси вращения, то это плоскопараллельное движение. Оно имеет мгновенную ось вращения, находящуюся на расстоянии от оси и удаленную от нее в сторону, перпендикулярно вектору .
Винтовое движение
Если скорости и постоянны, то шаг винта также постоянен и определяется по формуле: . При постоянных скоростях и , траекторией любой точки, не лежащей на оси винта, является винтовая линия. При этом скорость точки направлена по касательной к винтовой линии и имеет абсолютное значение , где r – расстояние до оси вращения; – скорость вращательного движения, перпендикулярная оси винта.
Поступательное движение под произвольным углом к оси вращения
Здесь скорость поступательного движения можно разложить на две составляющие – параллельную и перпендикулярную оси вращения . Рассматривая движение в плоскости, перпендикулярной оси вращения, мы можем найти мгновенный центр скоростей P . Он находится на расстоянии от оси . Прибавив сюда скорость , получим винтовое движение с осью . Если скорости меняются со временем, то ось будет мгновенной винтовой осью, а все движение можно рассматривать как состоящее из серии мгновенных винтовых движений вокруг непрерывно изменяющихся винтовых осей. Такое движение называется мгновенно–винтовым движением.
Использованная литература:
А. А. Яблонский, В.М. Никифорова. Курс теоретической механики, часть 1, статика, кинематика. Москва, «Высшая школа», 1966.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.
Автор: Олег Одинцов . Опубликовано: 17-08-2015 Изменено: 29-01-2020
Видео:Теоретическая механика 2020 - Практика 1. Кинематика точки.Скачать

Как найти уравнение траектории движения точки в полярной системе координат
В основе предлагаемой работы лежит опыт семинарских занятий по курсам общей физики и астрономии для студентов астрономического отделения физического факультета МГУ.
При изучении механики материальной точки, в особенности её разделов, связанных с движением по криволинейной траектории, часто оказываются полезными астрономические приложения. В условиях поверхности Земли набор естественных траекторий практически сводится к параболе. В космосе, наоборот, представлены многие типы криволинейного движения: вращение по окружности, а также эллиптические, параболические и гиперболические траектории разной степени вытянутости. К тому же формы орбит космических объектов не ограничиваются одними коническими сечениями. Например, обращение звёзд вокруг центра галактики во многих случаях не описываются законами Кеплера, а в процессе сжатия вращающихся газовых туманностей имеет место постепенное приближение к центру по спирали. Параллельно с физическим содержанием задачи уместно привести и первые сведения о математическом аппарате плоских кривых линий.
Другим аспектом является соотношение между прямыми и обратными задачами. Для лабораторных условий типична прямая постановка: требуется вычислить параметры траектории тела, зная действующие на него силы. В астрономии как наблюдательной науке важен и обратный подход, когда по известному движению выясняют характер взаимодействия. Часть предлагаемого материала даёт студентам первое представление об обратных задачах. С методической точки зрения решение обратной задачи, как правило, проще и нагляднее. Поэтому имеет смысл показать одну и ту же задачу дважды: сначала в разделе «кинематика» как обратную, и затем, после приобретения студентами опыта, в разделе «динамика» выполнить решение более сложной прямой задачи. Перейдём к изложению материала, предварительно договорившись о некоторых обозначениях. Координаты точки, движущейся в плоскости, как обычно, равны x и y , время — t , а для параметров движения оставляем буквы a , b , k , w , j . Векторы представляем прямыми жирными символами: r – радиус вектор частицы, v – её скорость, w – ускорение. Точка над символом описывает дифференцирование по времени.
I Определение траектории, скорости и ускорения точки из закона движения в декартовых координатах.
Во всех задачах этого раздела требуется определить форму траектории, найти векторы скорости и ускорения, а также восстановить динамический закон движения.
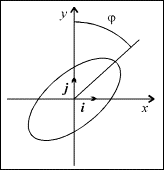
Задача 1 . Точка движется в плоскости. Её координаты x и y зависят от времени t как
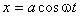
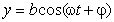
где a , b , ω и φ — параметры.
Если a либо b равны нулю, то имеет место прямолинейное движение вдоль той или иной координатной оси. Оно происходит внутри отрезка длиной 2 a , либо 2 b , центр которого расположен в начале координат. Предположим, что оба этих параметра отличны от нуля. Разделим первое уравнение на a , второе — на b и раскроем косинус суммы:
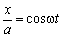
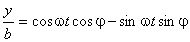
Исключим время t из уравнений движения. Сначала рассмотрим два особых случая. При 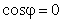
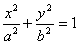
а значению 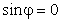
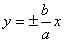
В случае, когда оба этих параметра отличны от нуля, с помощью ( 3 ) выразим 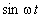
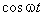
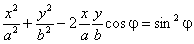
Роль параметра φ ясна из Рис. 1 . Теперь определим кинематические характеристики траектории и попытаемся выяснить направление действующей силы. На Рис. 1 единичные векторы i и j , направлены вдоль координатных осей. Напишем выражение для радиус-вектора точки, с координатами ( 1 ) и ( 2 ):
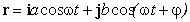
Векторы скорости и ускорения получаются последовательным дифференцированием r :
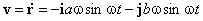
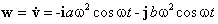
Из последних двух формул вытекает связь между ускорением и радиус-вектором:
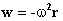
Мы получили хорошо известное уравнение пространственного осциллятора. Частица массы m движется под действием центральной притягивающей силы, по абсолютной величине равной mω 2 r .
Пространственный осциллятор является важным методическим инструментом в атомной физике и оптике — двух активно используемых в астрофизике разделах общей физики. Знакомство с ним на семинарах по механике облегчает в дальнейшем освоение темы поляризованного излучения, а также анализ эффектов Зеемана и Штарка.
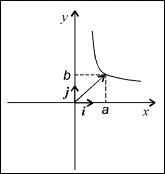
Задача 2 Точка движется по закону
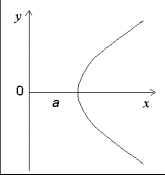
с параметрами a , b и k . Случай k =0 здесь не представляет интереса. Равенство нулю a или b означает прямолинейное перемещение вдоль одной из координатных осей. Если они оба отличны от нуля, то траектория является отрезком гиперболы y = ab / x .
Не теряя общности, мы можем считать a и b положительными [1] . Они равны координатам точки в начальный момент времени:
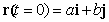
которая в дальнейшем будет двигаться вправо. Вычислим вектор скорости
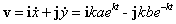
его абсолютную величину
и вектор ускорения
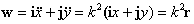
Тело отталкивает центральная сила mk 2 r .
Задача 3 . Точка движется в плоскости :
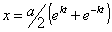
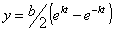
Вычтем квадраты уравнений, делённых на a и b соответственно:
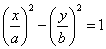
Получилась гипербола, как и на Рис. 2 , но оси координат повёрнуты на 45 ° . Её график приведён на Рис. 3 . Дифференцируя ( 6 ) и ( 7 ) по времени, получим вектор скорости
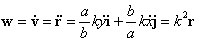
Легко убедиться, что и здесь на тело действует отталкивающая сила F = mk 2 r . Итак, одна и та же сила может обуславливать внешне различающиеся типы движения. На частном примере мы увидели проявление важного принципа: динамический закон является более общей характеристикой движения, чем кинематические параметры.
Задача 4 . Заряженная частица совершает пространственное движение в однородном и постоянном магнитном поле:
с постоянными параметрами R , vz , w . Складывая квадраты первых двух уравнений, получаем винтовую линию
с шагом 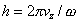
и квадрата его модуля 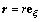
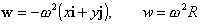
II . Движение в полярных координатах.
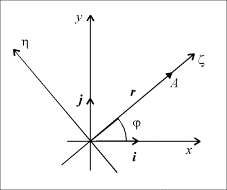
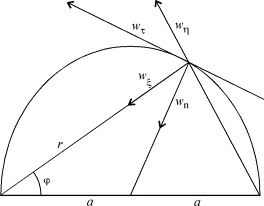
Задача 5 . Точка A движется в плоскости ( x, y), причём закон её движения задан в полярных координатах: r = r ( t ) , φ = φ ( t ) .
Определить скорость и ускорение точки.
Проведём дополнителные координатные оси ζ и η вдоль радиус-вектора и перпендикулярно ему как показано на Рис. 5 . Обозначим посредством eζ и e η “новые” единичные векторы вдоль осей ζ и η соответственно. Компонента любого вектора вдоль оси ξ называется радиальной, а вдоль оси η — трансверсальной. Если точка движется не по прямой линии, то векторы eζ и e η со временем меняют своё направление. Этим они отличаются от постоянных ортов i и j . Связь между двумя базисами даётся известной формулой вращения системы координат:
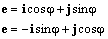
Дифференцируя первую строчку по времени и сравнивая результат со второй строкой, приходим к следующему выражению для 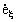
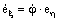
Радиус-вектор, по построению, коллинеарен e ζ ::
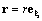
При вычислении вектора скорости в полярных координатах необходимо учитывать изменение направления орта 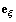
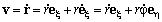

Проекция 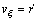
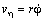
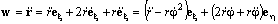
Описание движения во вращающейся системе отсчёта приобретает новые аспекты. В последней формуле 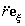
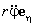
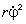
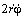
Задача 6 . Исходя из первого и второго законов Кеплера, определить ускорение планеты.
Планеты движутся по эллипсам, в одном из фокусов которого находится Солнце. Угол j отсчитываем от направления перигелия. Уравнение эллипса с эксцентриситетом e и параметром p в полярных координатах имеет вид:
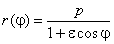
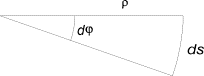
Второй закон Кеплера утверждает постоянство секторной скорости. Введём константу
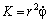
Перепишем формулу ( 9 ) Задача 5 в виде

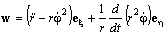
Легко видеть, что трансверсальная компонента вектора ускорения равна нулю. Ускорение направлено вдоль радиус–вектора Вычислим проекцию вектора w на ось ξ:
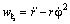
Вводим новую переменную u =1 / r и воспользуемся формулой Бинэ:
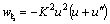
где введено обозначение 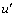
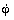
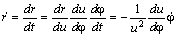
Воспользовавшись определениями 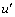
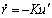
а дифференцируя его по времени с учётом ( 11 ) получаем
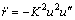
Подставляя в ( 13 ) полученные выражения для 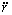
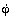
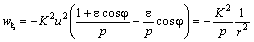
Итак, со стороны Солнца на планету действует притягивающая сила 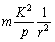
Задача 7 . Планета движется по эллипсу с эксцентриситетом ε. Зная её скорость v 1 в перигелии, определить скорость v 2 в афелии.
В этих двух точках орбиты ( и только в них ) скорость и радиус–вектор взаимно ортогональны. Следовательно, здесь модуль скорости v равен её трансверсальной компоненте: 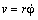
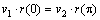
Воспользовавшись ( 10 ), приходим к окончательному результату:
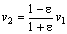
Задача 8 . Показать, что квадрат скорости планеты равен
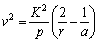
где a — длина большой полуоси. Из формулы ( 8 ) Задача 5 следует
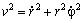
Вычислив 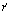
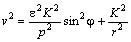
Здесь также учтено 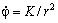
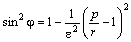
Подставив это значение в предыдущую формулу с учётом соотношения 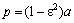
Задача 9 . Частица движется к притягивающему центру по плоской траектории
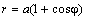
где r и φ — известные функции времени. В начальный момент времени угол φ равен нулю, а скорость тела направлена перпендикулярно радиус‑вектору и по абсолютной величине равна v 0. Полагаем, что сохраняется постоянной секторная скорость, то есть справедлива формула ( 11 ). Определить зависимость скорости от расстояния r до притягивающего центра, а также трансверсальную и радиальную компоненты ускорения.
Из начальных условий определим значение константы K =2 av 0. Согласно ( 12 ), трансверсальное ускорение равно нулю вследствие постоянства секторной скорости. Таким образом, притягивающая сила направлена вдоль радиус‑вектора. Радиальную компоненту вычислим двумя способами. Сначала выполним прямые расчёты по формуле ( 13 ) Задача 6 . Из ( 15 ) и ( 16 ) следуют выражения для 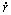
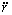
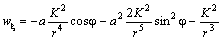
Теперь с помощью ( 18 ) выражаем cosφ и sin 2 φ через a и r :
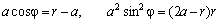
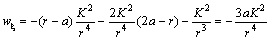
Теперь воспользуемся формулой Бинэ ( 14 ) и уравнением траектории ( 18 ):
Подставляя в ( 14 ) полученное выражение для 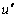
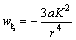
Связь между модулями скорости и радиус‑вектора проще всего вычислить с помощью формулы ( 17 ):
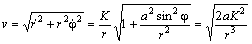
Задача 10 . Точка движется в плоскости по закону
с параметрами r 0 и a . Определить траекторию, скорость и обе компоненты ускорения.
Исключив время t , получим изображённую на Рис. 6 гиперболическую спираль
Рис. 6 Падение на центр
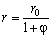
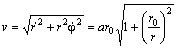
Начальный наклон траектории на Рис. 6 определяется соотношением между двумя компонентами скорости. По формуле ( 8 ) легко найти, что для начального момента времени: 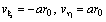
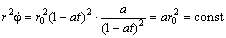
Следовательно, трансверсальное ускорение равно нулю; т.е. притягивающая сила направлена вдоль радиус‑вектора. По формуле ( 13 ) определим радиальное ускорение
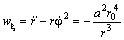
Таким образом, частица падает на притягивающий центр под действием силы, обратно пропорциональной кубу расстояния.
III Проекция ускорения на естественные оси.
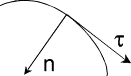
Естественными осями при изучении криволинейного движения на плоскости принято считать касательную и нормаль к траектории. Тангенциальная и нормальная компоненты векторов часто позволяют полнее раскрыть физический смысл рассматриваемого движения. Вводимые ниже понятия напоминают те, которыми мы пользовались в полярной системе координат, но они не зависят от выбора системы отсчёта.
Задача 11 . Движение точки в плоскости описывается в декартовых координатах как x = x ( t ), y = y ( t ). Определить проекции скорости и ускорения на естественные оси, а также радиус кривизны траектории.
Рис. 7 . Касательная и нормаль
Направим координатные оси τ и n вдоль касательной и нормали к траектории, как показано на Рис. 7 . Обозначим eτ и e n единичные векторы вдоль соответствующих осей. Вектор eτ направлен вдоль скорости:
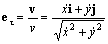
Формула 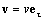
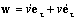
Так как длина вектора 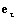
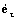
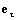
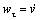
Вектор нормали e n ищем в виде
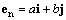
где подлежащие определению проекции a и b удовлетворяют условиям нормировки
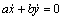
Из двух решений этой системы уравнений мы выбираем такое, при котором вектор нормали направлен в сторону вогнутости траектории, как на Рис. 7 :
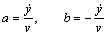
Проекция ускорения на касательную w τ равна скалярному произведению
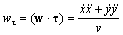
Аналогично вычисляем w n :
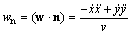
Перейдём к вычислению радиуса кривизны ρ траектории в данной точке. Он задаётся условием
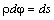
где ds — смещение вдоль траектории, соответствующее изменению угла d φ . Обе эти величины на Рис. 8 считаем бесконечно малыми. Следовательно, можно пренебречь изменением абсолютной величины скорости на отрезке ds и воспользоваться известной формулой для центростремительного ускорения при равномерном движении по окружности:
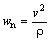
Подставляя сюда ( 21 ), приходим к
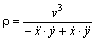
Радиус кривизны бесконечно велик в случае прямолинейной траектории.
Задача 12 . Точка описывает эллипс

Определить нормальную и тангенциальную компоненты ускорения, а также радиус кривизны траектории в точках A и B Рис. 9 .
Рассматриваемое движение является частным случаем Задача 1 . Подставив ( 5 ) в ( 20 ), приходим к
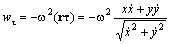
Аналогичным путём получаем формулы для нормального ускорения
и для радиуса кривизны
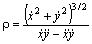
Подставляя в них зависимость x и y от времени, получаем для точки A :
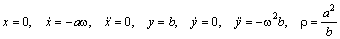
Задача 13 . Частица движется в плоскости по траектории r = a cosφ . В начальный момент времени φ=0, а скорость направлена перпендикулярно радиус‑вектору. Секторная скорость постоянна и равна K / 2. Определить связь между модулями v и r , а также компоненты ускорения: тангенциальную, нормальную, радиальную и трансверсальную.
При постоянном K величина v однозначно выражается уравнением траектории:
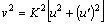
Здесь мы воспользовались обозначениями Задача 6 и формулой ( 15 ). Подставляя
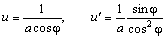
приходим к следующему выражению для v 2 :
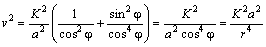
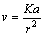
Рис. 10 . Компоненты вектора ускорения.
В интервале углов 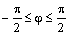
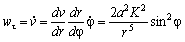
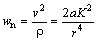
Трансверсальное ускорение равно нулю. Вычисление радиальной компоненты можно упростить следующим образом. Нам известны компоненты вектора 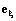
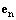
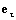
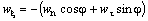
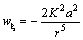
[1] Знаки a и b определяют квадрант, в котором находится гипербола.
🔍 Видео
Полярная система координат.Скачать

Площадь фигуры, заданной в полярной системе координатСкачать

7.1. Траектория и положение точки в прямоугольной системе координатСкачать

Лекция 5.3 | Уравнение траектории | Александр Чирцов | ЛекториумСкачать

Как построить точки в системе координат OXYZСкачать

Глаза гипножабы и площадь фигур в полярной системе координатСкачать

§12 Полярное уравнение прямойСкачать

Занятие 01. Часть 3. Полярная система координатСкачать

Кинематика точки Задание К1Скачать

Способы описания движения. Траектория. Путь. ПеремещениеСкачать

Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать