С помощю этого онлайн калькулятора ромба можно найти длину стороны ромба по известным элементам. Для нахождения стороны ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
| Открыть онлайн калькулятор |
- 1. Сторона ромба через высоту и площадь
- 2. Сторона ромба через высоту и угол
- 3. Сторона ромба через диагонали
- 4. Сторона ромба через угол и противолежащую диагональ
- 5. Сторона ромба через угол и диагональ из данного угла
- 6. Сторона ромба через площадь и радиус вписанной в ромб окружности
- 7. Сторона ромба через площадь и угол
- Электронная библиотека
- как составить уравнения сторон ромба.
- 🎦 Видео
Видео:Уравнения стороны треугольника и медианыСкачать
1. Сторона ромба через высоту и площадь
Пусть известны площадь и высота ромба (Рис.1).
 |
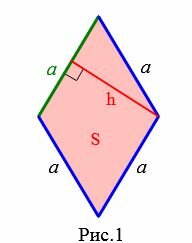Покажем, что сторона ромба через высоту и площадь вычисляется формулой
| (small a=frac.) | (1) |
Формула площади ромба через сторону и высоту имеет следующий вид:
| (small S=a cdot h.) |
Откуда легко вывести формулу (1).
Видео:Вычисляем высоту через координаты вершин 1Скачать
2. Сторона ромба через высоту и угол
Рассмотрим ромб с высотой h и углом α между сторонами (Рис.2). Выведем формулу вычисления стороны ромба через высоту и угол.
 |
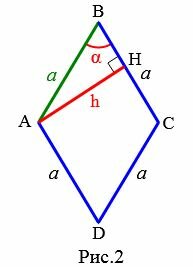Для прямоугольного треугольника AHB применим теорему синусов:
| (small frac=frac.) |
Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:
| (small a=frac.) | (2) |
Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: (small angle C=180°-alpha.) Следовательно (small sin angle C=sin(180°-alpha)=sin alpha.) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.
Видео:Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать
3. Сторона ромба через диагонали
Выведем формулу вычисления сторон ромба через диагонали.
Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).
 |
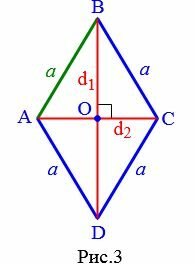Применим к прямоугольному треугольнику AOB теорему Пифагора:
| (small a^2= left( frac right)^2+left( frac right)^2.) |
| (small a= frac<sqrt> ) | (3) |
Видео:№477. Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромбаСкачать
4. Сторона ромба через угол и противолежащую диагональ
Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления сторон ромба.
 |
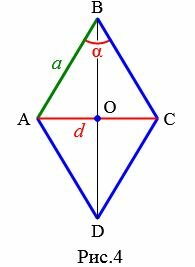Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Кроме этого, диагонали ромба делят углы ромба пополам. Применим теорему синусов для прямоугольного треугольника AOB:
| (small frac=frac<large frac><large sin frac>.) |
Откуда получим формулу стороны ромба через угол и противолежащую диагональ:
| (small a=frac<large 2 cdot sin frac>.) | (4) |
Формулу (4) можно записать и в другом виде, применяя формулу синуса половинного угла:
| (small sin frac=sqrt<frac>.) | (5) |
Подставляя (5) в (4), получим:
| (small a=frac<large 2 cdot sqrt<frac>>.) |
| (small a=large frac< sqrt>.) | (6) |
Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать
5. Сторона ромба через угол и диагональ из данного угла
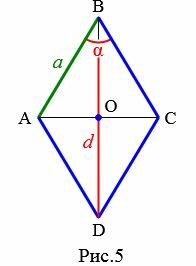
Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.
 |
Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Для прямоугольного треугольника AOB, имеем:
| (small frac =cos angle ABO.) | (7) |
Учитывая, что ( small BO=frac) и ( small angle ABO=frac), формулу (13) можно записать так:
| (small frac< large frac >= cos frac .) |
| (small a=frac<large 2 cdot cos large frac>.) | (8) |
Формулу (8) можно записать и в другом виде, применяя формулу косинуса половинного угла:
| (small cos frac=sqrt<frac>.) | (9) |
Подставляя (9) в (8), получим:
| (small a=frac<large 2 cdot sqrt<frac>>.) |
| (small a=large frac< sqrt>.) | (10) |
Видео:№493. Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см.Скачать
6. Сторона ромба через площадь и радиус вписанной в ромб окружности
В статье Площадь ромба показали, что площадь ромба через сторону и радиус вписанной в ромб окружности вычисляется формулой
| (small S= 2 cdot a cdot r.) | (11) |
Из формулы (11) получим:
| ( small a=frac ) | (12) |
Видео:№980. Напишите уравнения прямых, содержащих стороны ромба, диагонали которого равны 10 см и 4 см,Скачать
7. Сторона ромба через площадь и угол
В статье Площадь ромба показали, что площадь ромба через сторону и угол вычисляется формулой
| (small S= a^2 cdot sin alpha.) | (13) |
Из формулы (13) найдем a:
| ( small a=frac ) | (14) |
Получили формулу сторон ромба через площадь и угол.
Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать
Электронная библиотека
Пример 1. Вычислить координаты вершин ромба, если известны уравнения двух его сторон: и и уравнение одной из его диагоналей: . Решение. Выясним взаимное расположение известных сторон ромба. Угловой коэффициент k прямой определяется по формуле:
Стороны параллельны, так как имеют одинаковый угловой коэффициент:
Для построения рисунка (рис. 4.1) запишем уравнения в отрезках для данных прямых:
Наметим план решения: 1) находим вершины ромба P и Q ; 2) находим точку пересечения диагоналей ромба N ; 3) через точку N проводим диагональ D 2 ; 4) находим оставшиеся вершины ромба R и S .1) Так как точка P является точкой пересечения прямых L 2 и D 1 , то ее координаты находим из системы уравнений:
Из рис. 4.1 сразу находим координаты точки Q (- 2, 0) . 2) Так как диагонали ромба в точке пересечения делятся пополам, то точка является серединой отрезка PQ , поэтому ее координаты — полусумма соответствующих координат точек P и Q :
3) Так как диагонали ромба взаимно перпендикулярны, то прямая D 2 перпендикулярна вектору . Найдем его координаты:
По формуле (3.1) находим уравнение диагонали D 2 как уравнение прямой, проходящей через точку N (- 3, 1) перпендикулярно вектору = :
2( x — (- 3)) + (- 2)( y — 1) = 0, x — y + 4 = 0.
4) Вершины ромба R и S — точки пересечения прямых L 2 и D 2 , L 1 и D 2 , соответственно, находим из уравнений:
Ответ: P (- 4, 2) R (- 6, — 2), Q (- 2, 0), S (0, 4).
Пример 2. Составить уравнения сторон треугольника, зная одну его вершину P (2, — 7), уравнения высоты 3 x + y + 11 = 0 и медианы x + 2 y + 7 = 0, проведенных из разных вершин. Решение. Для построения рисунка (рис. 4.2) приведем уравнения данных прямых к уравнениям в отрезках:
h : 3 x + y + 11 = 0, m : x + 2 y + 7 = 0 ,
План решения:1) находим уравнение прямой PQ ;2) находим координаты точки R ;3) находим уравнения прямых RP и RQ .1) Находим нормальный вектор прямой h : . Уравнение стороны PQ , проходящей через точку P (2, — 7) параллельно вектору , запишем в виде:
Находим координаты точки Q — точки пересечения прямых PQ и m :
2) По свойству медианы треугольника PQR точка S ( x S , y S ) является серединой отрезка RP . Следовательно:
Точка S лежит на медиане m , значит,
Точка R лежит на высоте h , значит,
Из последних двух уравнений определяем координаты точки R , решая систему: 3) Используя формулу (3.4), составим уравнение прямой RP , проходящей через две заданные точки R и P : Аналогично, составим уравнение прямой RQ : Ответ: x — 3 y — 23 = 0, ,
Видео:ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать
как составить уравнения сторон ромба.
как составить уравнения сторон ромба ABCD и найти его площадь, если известны уравнения сторон AB u BC и координаты вершины Д.
АВ: 2x+y-2=0
BC: 2x-y-2=0
D(4,2)
составить уравнение прямой проходящей через точку А, перпендикулярно к плоскости, которая проходит через точки А, В и С.
А (0,-1,0) В (2,1,-2) С (1,4,1)
Найти точку пересечения плоскости ХОУ и прямой проходящей через точки А и В.
А (-9,7,-2) В (-11,2,3)
найти проекцию точки А на прямую, заданную как пересечение двух плоскостей.
А (-2,1,-1)
1: x+4y+2z-3=0
2: 2x+5y+z=0
найти радиус и координаты центра окружности, заданной уравнением:
x^2+y^2+6x-8y=0
4. приведи к виду (x-a)^2 + (y-b)^2 = r^2, тогда А и В — координаты центра,
🎦 Видео
№407. Найдите углы, которые образуют диагонали ромба с его сторонами, если одинСкачать
Встреча с Путиным в общежитии МГУ на Воробьевых горах!Скачать
Задание 17 ОГЭ по математике. Ромб. Найти высоту ромба.Скачать
№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать
Уравнение прямой и треугольник. Задача про высотуСкачать
Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать
Вычисление медианы, высоты и угла по координатам вершинСкачать
ОГЭ 23 | КАК НАЙТИ ВЫСОТУ РОМБА | Если известны отрезки, на которые высота делит сторонуСкачать
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
Найти площадь ромба.Скачать
№494. Найдите диагональ и площадь ромба, если его сторона равна 10 см, а другая диагональ — 12 см.Скачать
