Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
Видео:Угловой коэффициент прямойСкачать
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Видео:Уравнения стороны треугольника и медианыСкачать  Консультации по отчетам к практике, контрольные, курсовыеДля решения задачи требуется знание координат точек А(-5; 0) и В(7;9). Для нахождения длины отрезка АВ используем формулу расстояния между точками:
Для нахождения длины отрезка АВ используем формулу длины вектора:
Что бы найти координаты вектора, нужно из соответствующих координат конца, вычесть соответствующие координаты начала:
Длину вектора найдем по формуле:
Тогда Написать уравнения сторон АВ и АС и найти их угловые коэффициенты Напишем уравнение прямой АВ, используя уравнение прямой проходящей через две точки:
3х-4у+15=0 – уравнение прямой АВ Для нахождения углового коэффициента выразим из уравнения переменную у: у= тогда угловой коэффициент прямой АВ: угловой коэффициент этой прямой можно найти по формуле:
аналогично составим уравнение прямой АС:
х+2у-5=0 – уравнение прямой АС Определим угловой коэффициент:
Или Определить внутренний угол А в радианах с точностью до 0,01 Для определения внутреннего угла при вершине А используем формулу угла между прямыми АВ и АС:
Из пункта №2:
Для определения внутреннего угла при вершине А используем формулу угла между векторами
Определим координаты векторов:
Найдем длины данных векторов: Найдем скалярное произведение векторов:
Подставим все данные в формулу угла между векторами: 🎥 ВидеоМатематика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать  №973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать  Даны координаты вершин треугольника АВС.Скачать  7 класс - Алгебра - Определение углового коэффициентаСкачать  Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  Вычисляем высоту через координаты вершин 1Скачать  Аналитическая геометрия на плоскостиСкачать  Математика без Ху!ни. Уравнение плоскости.Скачать  Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать  найти уравнение высоты треугольникаСкачать  Уравнение прямой и треугольник. Задача про высотуСкачать  Аналитическая геометрия на плоскости. Решение задачСкачать  10 класс, 43 урок, Уравнение касательной к графику функцииСкачать  Вычисление медианы, высоты и угла по координатам вершинСкачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  Уравнения прямой на плоскости | Векторная алгебраСкачать  №942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать  | ||
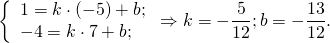
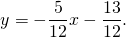
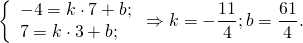
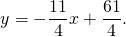
ед. дл.
ед. дл.
ед. дл.
,
, 
,
ед. дл.