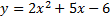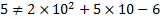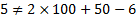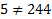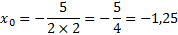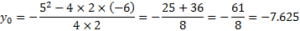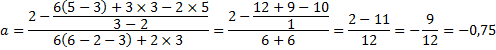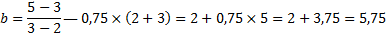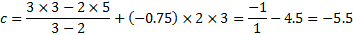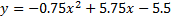Как найти уравнение параболы проходящей через точки

Видео:Составляем уравнение прямой по точкамСкачать

Уравнение по трем точкам: как найти вершину параболы, формула

Многие технические, экономические и социальные вопросы прогнозируются при помощи кривых. Наиболее используемым типом среди них является парабола, а точнее, ее половина. Важной составляющей любой параболической кривой является ее вершина, определение точных координат которой иногда играет ключевую роль не только в самом отображении протекания процесса, но и для последующих выводов. О том, как найти ее точные координаты, и пойдет речь в данной статье….

Видео:Как легко составить уравнение параболы из графикаСкачать

Начало поиска

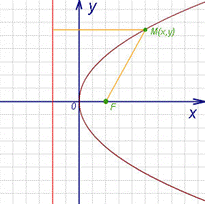
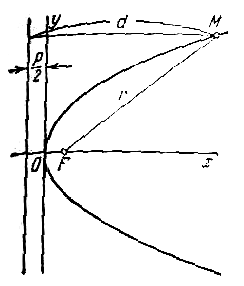
Перед тем как перейти к поиску координат вершины параболы, ознакомимся с самим определением и его свойствами. В классическом понимании параболой называется такое расположение точек, которые удалены на одинаковом расстоянии от конкретной точки (фокус, точка F), а также от прямой, которая не проходит через точку F. Рассмотрим данное определение более предметно на рисунке 1.

Рисунок 1. Классический вид параболы

На рисунке изображена классическая форма. Фокусом является точка F. Директрисой в данном случае будет считаться прямая параллельная оси Y (выделена красным цветом). Из определения можно удостовериться, что абсолютно любая точка кривой, не считая фокуса, имеет себе подобную с другой стороны, удаленную на таком же расстояние от оси симметрии, как и сама. Более того, расстояние от любой из точек на параболе равно расстоянию до директрисы. Забегая вперед, скажем, что центр функции не обязательно должен находиться в начале координат, а ветки могут быть направлены в разные стороны.

Парабола, как и любая другая функция, имеет свою запись в виде формулы:

(1).

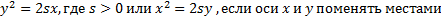
В указанной формуле буква «s» обозначает параметр параболы, которая равна расстоянию от фокуса до директрисы. Также есть и другая форма записи, указано ГМТ, имеющая вид:

(2).

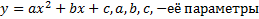
Такая формула используется при решении задач из области математического анализа и применяется чаще, чем традиционная (в силу удобства). В дальнейшем будем ориентироваться на вторую запись.

Это интересно! Первый признак равенства треугольников: доказательство

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Расчет коэффициентов и основных точек параболы

К числу основных параметров принято относить расположение вершины на оси абсцисс, координаты вершины на оси ординат, параметр директрисы.

Численное значение координаты вершины на оси абсцисс

Если уравнение параболы задано в классическом виде (1), то значение абсциссы в искомой точке будет равняться половине значения параметра s (половине расстояния между директрисой и фокусом). В случае, если функция представлена в виде (2), то x нулевое рассчитывается по формуле:

(3).

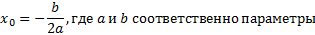
Т.е., глядя на эту формулу, можно утверждать, что вершина будет находиться в правой половине относительно оси y в том случае, если один из параметров a или b будет меньше нуля.

Уравнение директрисы определяется следующим уравнением:

(4).

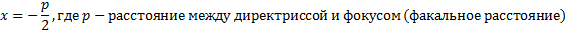
Это интересно! Что такое деление с остатком: примеры для ребенка в 3, 4 классе

Значение вершины на оси ординат

Численное значение местонахождения вершины для формулы (2) на оси ординат можно найти по такой формуле:

.

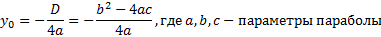
Отсюда можно сделать вывод, что в случае если а&lt,0, то вершина кривой будет находиться в верхней полуплоскости, в противном случае – в нижней. При этом точки параболы будут обладать теми же свойствами, что были упомянуты ранее.

Если дана классическая форма записи, то более рациональным будет вычисление значения расположения вершины на оси абсцисс, а через него и последующее значение ординаты. Отметим, что для формы записи (2), ось симметрии параболы, в классическом представлении, будет совпадать с осью ординат.

Важно! При решении заданий с использованием уравнения параболы прежде всего выделите основные значения, которые уже известны. Более того, нелишним будет, если будут определены недостающие параметры. Такой подход заранее даст большее «пространство для маневра» и более рациональное решение. На практике старайтесь использовать запись (2). Она более проста для восприятия (не придется «переворачивать координаты Декарта), к тому же подавляющее количество заданий приспособлено именно под такую форму записи.

Это интересно! Чему равна и как найти площадь равностороннего треугольника

Видео:Как найти уравнение параболы Найти коэффициент а через точки ОГЭ математика задание 5Скачать

Построение кривой параболического типа

Используя распространенную форму записи, перед тем как построить параболу, требуется найти ее вершину. Проще говоря, необходимо выполнить следующий алгоритм:

1. Найти координату вершину на оси X.
2. Найти координату расположения вершины на оси Y.
3. Подставляя разные значения зависимой переменной X, найти соответствующие значения Y и построить кривую.

Т.е. алгоритм не представляет собой ничего сложного, основной акцент делается на том, как найти вершину параболы. Дальнейший процесс построения можно считать механическим.

При условии, что даны три точки, координаты которых известны, прежде всего необходимо составить уравнение самой параболы, а потом повторить порядок действий, который был описан ранее. Т.к. в уравнении (2) присутствуют 3 коэффициента, то, используя координаты точек, вычислим каждое из них:

(5.1).

(5.2).

(5.3).

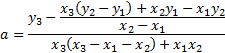
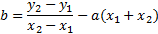
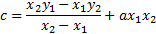
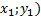
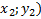
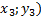
В формулах (5.1), (5.2), (5.3) применяются соответственно тех точек, которые известны (к примеру А ( , B (, C ( . Таким путем находим уравнение параболы по 3 точкам. С практической стороны такой подход не является самым «приятным», однако он дает четкий результат, на основе которого впоследствии строится сама кривая.

При построении параболы всегда должна присутствовать ось симметрии. Формула оси симметрии для записи (2) будет иметь такой вид:

(6).

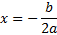
Т.е. найти ось симметрии, которой симметричны все точки кривой, не составляет труда. Точнее, она равна первой координате вершины.

Это интересно! Изучаем математику в игровой форме: как ребенку быстро выучить таблицу умножения

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Наглядные примеры

Пример 1. Допустим, имеем уравнение параболы:

Требуется найти координаты вершины параболы, а также проверить, принадлежит ли точка D (10, 5) данной кривой.

Решение: Прежде всего проверим принадлежность упомянутой точки самой кривой

Откуда делаем вывод, что указанная точка не принадлежит заданной кривой. Найдем координаты вершины параболы. Из формул (4) и (5) получаем такую последовательность:

Получается, что координаты на вершине, в точке О, следующие (-1,25, -7,625). Это говорит о том, что наша парабола берет свое начало в 3-й четверти декартовой системы координат.

Пример 2. Найти вершину параболы, зная три точки, которые ей принадлежат: A (2,3), B (3,5), C (6,2). Используя формулы (5.1), (5.2), (5.3), найдем коэффициенты уравнения параболы. Получим следующее:

Используя полученные значения, получим следующие уравнение:

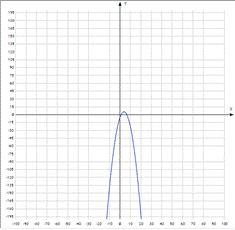
На рисунке заданная функция будет выглядеть следующим образом (рисунок 2):

Рисунок 2. График параболы, проходящий через 3 точки

Т.е. график параболы, который проходит по трем заданным точкам, будет иметь вершину в 1-й четверти. Однако ветки данной кривой направлены вниз, т.е. имеется смещение параболы от начала координат. Такое построение можно было предвидеть, обратив внимание на коэффициенты a, b, c.

В частности, если a&lt,0, то ветки» будут направлены вниз. При a&gt,1 кривая будет растянута, а если меньше 1 – сжата.

Константа c отвечает за «движение» кривой вдоль оси ординат. Если c&gt,0, то парабола «ползет» вверх, в противном случае – вниз. Относительно коэффициента b, то определить степень влияния можно лишь изменив форму записи уравнения, приведя ее к следующему виду:

Если коэффициент b&gt,0, то координаты вершины параболы будут смещены вправо на b единиц, если меньше – то на b единиц влево.

Важно! Использование приемов определения смещения параболы на координатной плоскости подчас помогает экономить время при решении задач либо узнать о возможном пересечении параболы с другой кривой еще до построения. Обычно смотрят только на коэффициент a, так как именно он дает четкий ответ на поставленный вопрос.

Полезное видео: как найти вершину параболы

Полезное видео: как легко составить уравнение параболы из графика

Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

Вывод

Такой как алгебраический процесс, как определение вершин параболы, не является сложным, но при этом достаточно трудоемкий. На практике стараются использовать именно вторую форму записи с целью облегчения понимания графического решения и решения в целом. Поэтому настоятельно рекомендуем использовать именно такой подход, и если не помнить формулы координаты вершины, то хотя бы иметь шпаргалку.

Видео:12. Уравнения прямой в пространстве Решение задачСкачать

Как найти уравнение параболы проходящей через точки

Видео:Как определить уравнение параболы по графику?Скачать

Глава 20. Парабола

Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

(1)

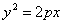
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

.

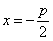
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле

.

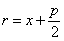
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

(2)

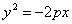
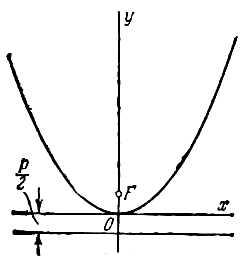
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

(3)

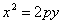
если она лежит в верхней полуплоскости (рис.), и

(4)

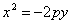
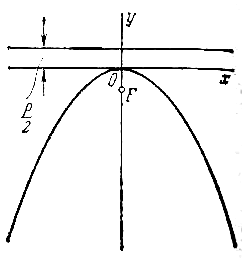
если в нижней полуплоскости (рис.)

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

Видео:Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?

Урок: как построить параболу или квадратичную функцию?

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Парабола — это график функции описанный формулой ax 2 +bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:

1 ) Формула параболы y=ax 2 +bx+c,
если а>0 то ветви параболы направленны вверх,
а 2 +bx+c=0;

a) Полное квадратное уравнение имеет вид ax 2 +bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax 2 +bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);

4) Найти несколько дополнительных точек для построения функции.

ПРАКТИЧЕСКАЯ ЧАСТЬ

И так теперь на примере разберем все по действиям:
Пример №1:
y=x 2 +4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x 2 +4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x₁=(-4+2)/2=-1
x₂=(-4-2)/2=-3

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2

х -4 -3 -1 0
у 3 0 0 3

Подставляем вместо х в уравнение y=x 2 +4x+3 значения
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2

Пример №2:
y=-x 2 +4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1 2 +4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x 2 +4x=0
Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x 2 +4x значения
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2

Пример №3
y=x 2 -4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x 2 -4=0
Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x 2 =4
x₁=2
x₂=-2

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x 2 -4 значения
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0

Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.

📹 Видео

Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

213. Фокус и директриса параболы.Скачать

Как написать уравнение параболы с помощью графикаСкачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

§24 Каноническое уравнение параболыСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Как найти все коэффициенты параболы по графику? Большой ответ на этот вопрос.Скачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Составить уравнение прямой, проходящей через две данные точки. Метод координат. Геометрия 9 классСкачать