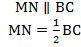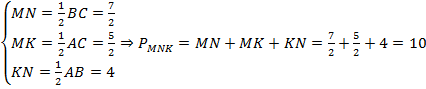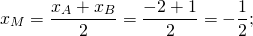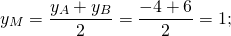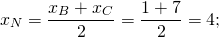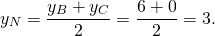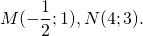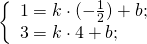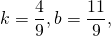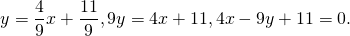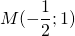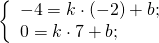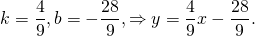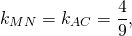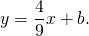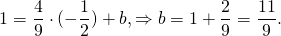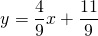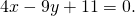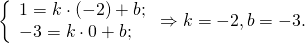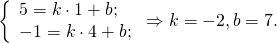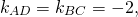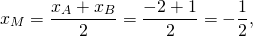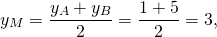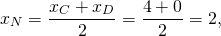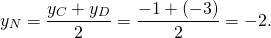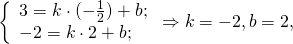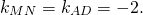Как найти уравнение линии в треугольнике

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Видео:Уравнение прямой и треугольник. Задача про высотуСкачать

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

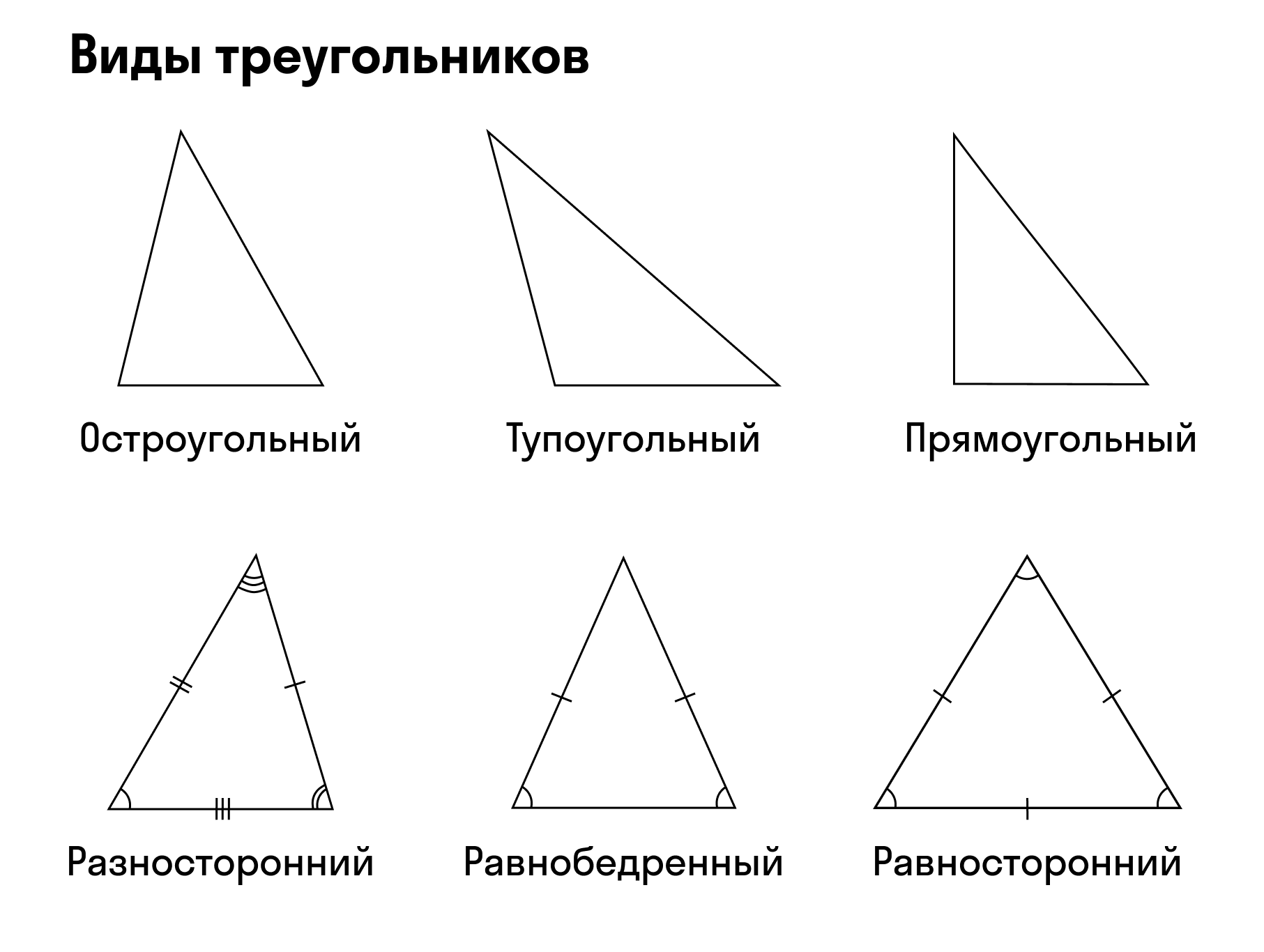
• Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
• Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
• Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

• В треугольнике против большего угла лежит большая сторона — и наоборот.
• Сумма углов треугольника равна 180 градусов.
• Все углы равностороннего треугольника равны 60 градусам.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

​Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

​Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Видео:Уравнения стороны треугольника и медианыСкачать

Понятие средней линии прямоугольного треугольника

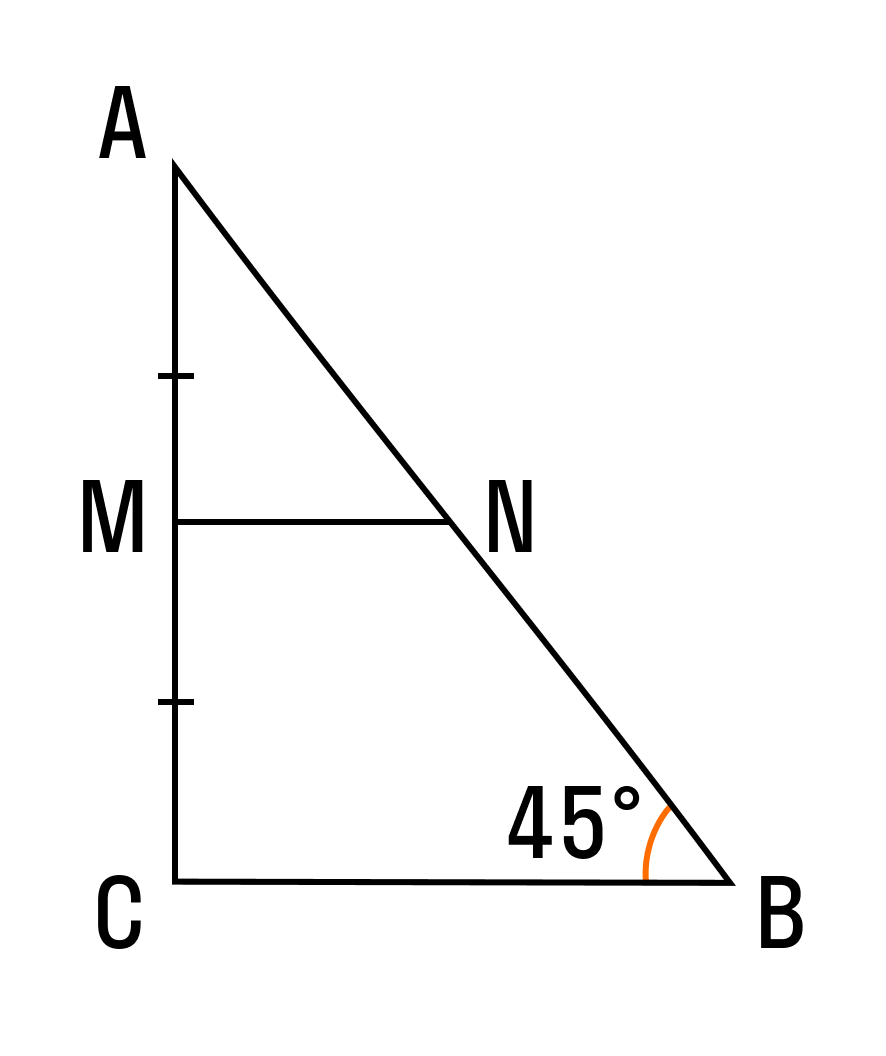
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Видео:Вычисляем высоту через координаты вершин 1Скачать

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

1. Средняя линия равна половине длины основания и параллельна ему.
2. Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

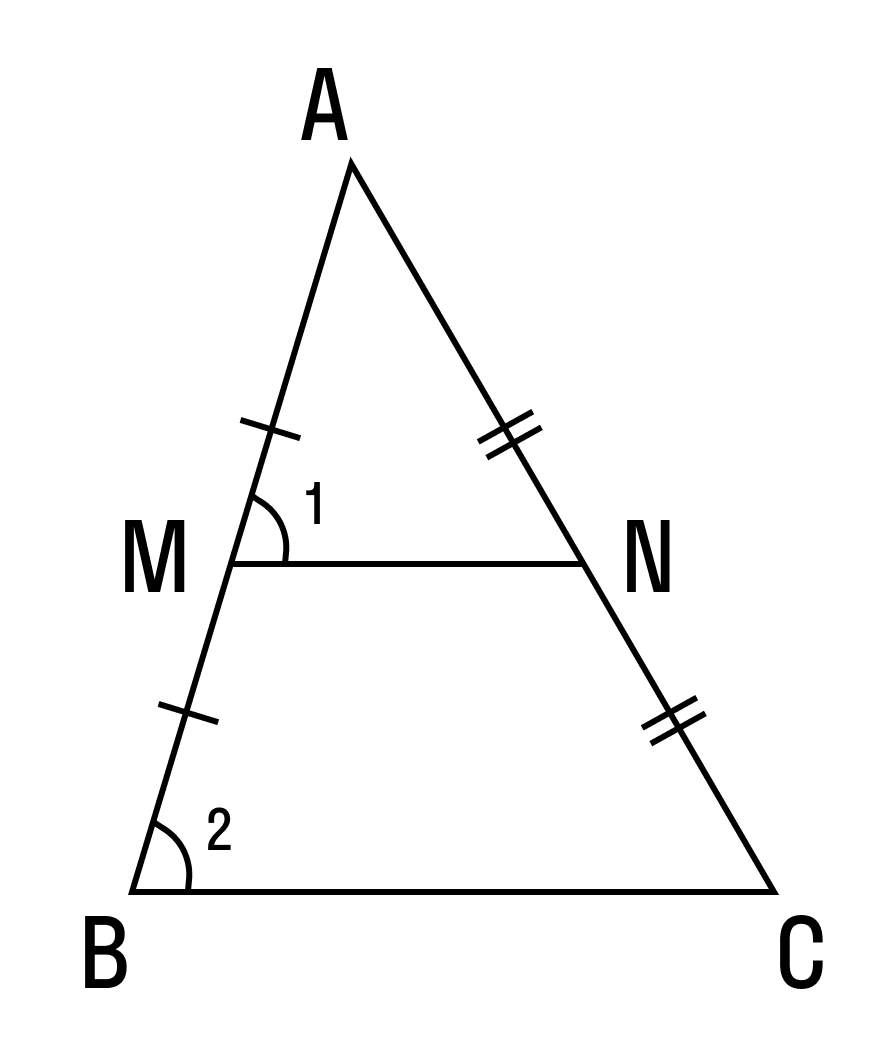
Докажем теорему:

По условию нам дано, что MA = MB, NA = NC

Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

(по второму признаку подобия треугольников).

△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.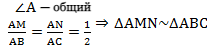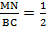

△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.

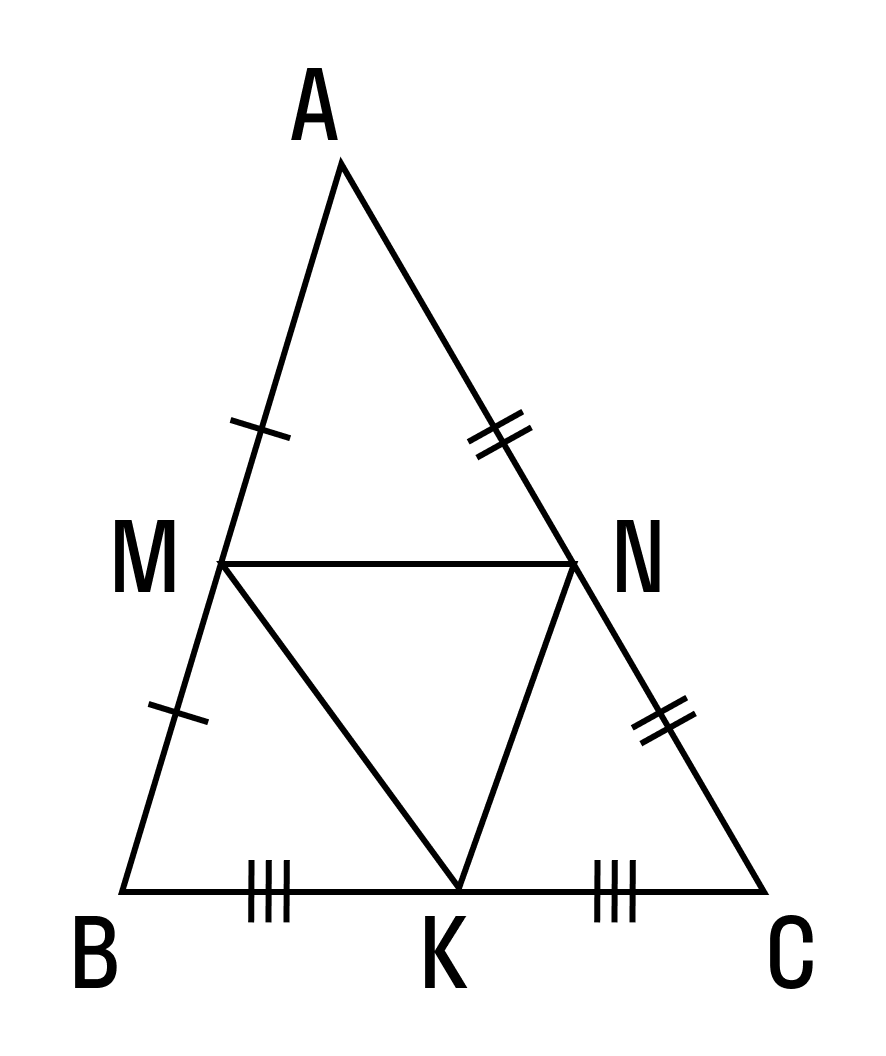
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

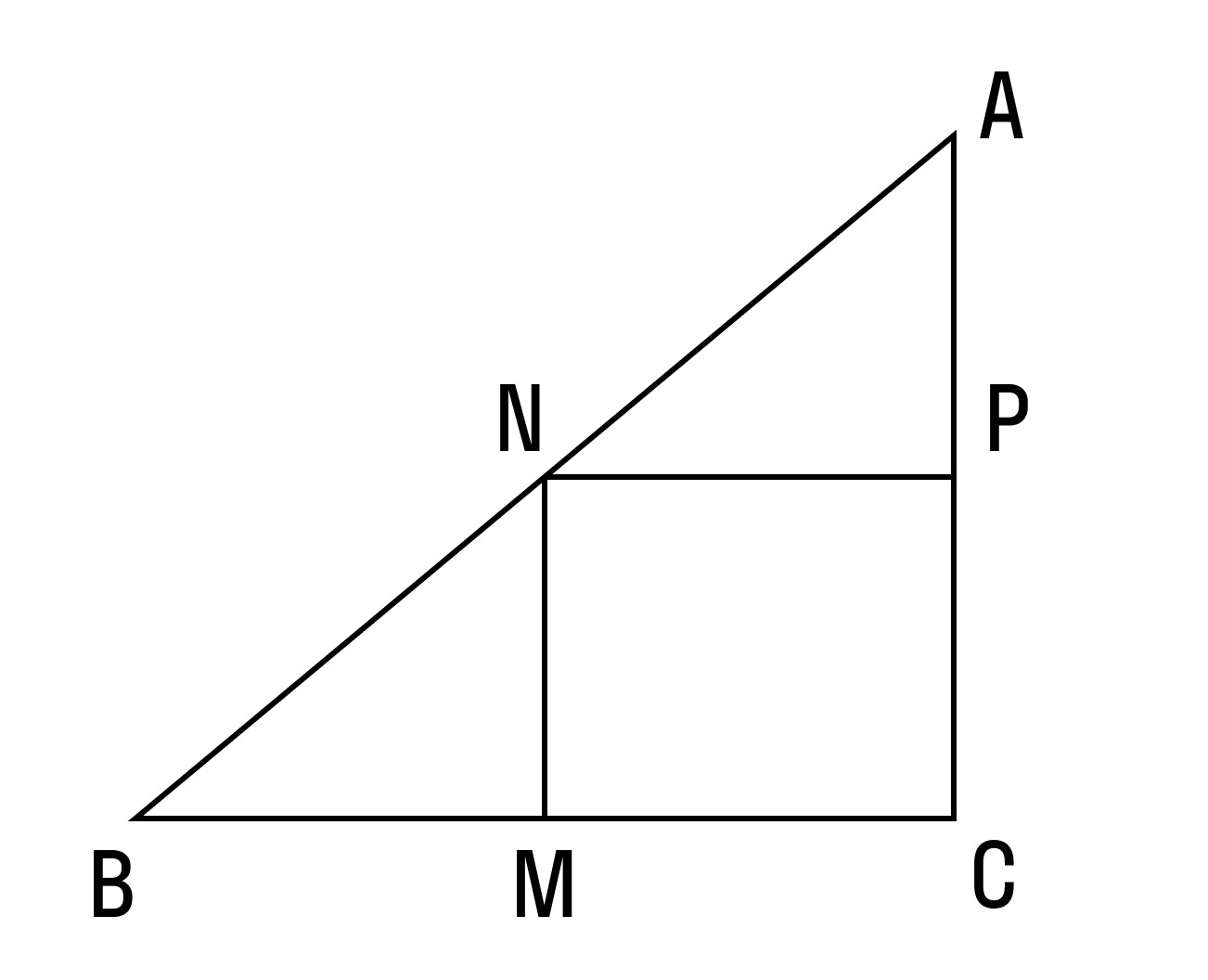
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение средней линии

Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?

Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.

Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.

1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.

М — середина отрезка AB, N — середина BC.

Составим уравнение прямой MN, например, в виде y=kx+b:

Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.

— середина отрезка AB. Составим уравнение прямой AC:

Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.

Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:

то есть уравнение прямой MN ищем в виде

Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:

Таким образом, уравнение прямой MN

Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.

Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).

Сначала следует определить основания данной трапеции.

Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.

Значит, уравнение прямой AD: y= -2k-3.
B(1;5), C(4;-1),

Уравнение прямой BC: y= -2k+7.

Поскольку угловые коэффициенты прямых равны:

то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины AB и CD соответственно.

Составим уравнение прямой MN, M(-1/2;3), N(2;-2):

Уравнение AD — y= -2k-3, середина AB — M(-1/2;3). Составляем уравнение прямой MN, параллельной прямой AD.

Значит уравнение MN ищем в виде y= -2x+b.

Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:

Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.

Видео:найти уравнение высоты треугольникаСкачать

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте через точку, а не запятую. Округлять до -го знака после запятой. 🎥 Видео Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать Математика без Ху!ни. Уравнение плоскости.Скачать Составляем уравнение прямой по точкамСкачать найти уравнения биссектрис углов между прямымиСкачать 9 класс, 7 урок, Уравнение прямойСкачать Уравнения прямой на плоскости | Векторная алгебраСкачать Средняя линия. Теорема о средней линии треугольникаСкачать Математика это не ИсламСкачать Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать Вычисление медианы, высоты и угла по координатам вершинСкачать Написать канонические и параметрические уравнения прямой в пространствеСкачать Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать Уравнение прямой по двум точкамСкачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства