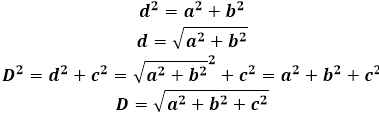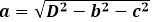Как найти уравнение диагональной плоскости параллелепипеда

Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Прямоугольный параллелепипед. Что это такое?

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Видео:Как строить сечения параллелепипедаСкачать

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

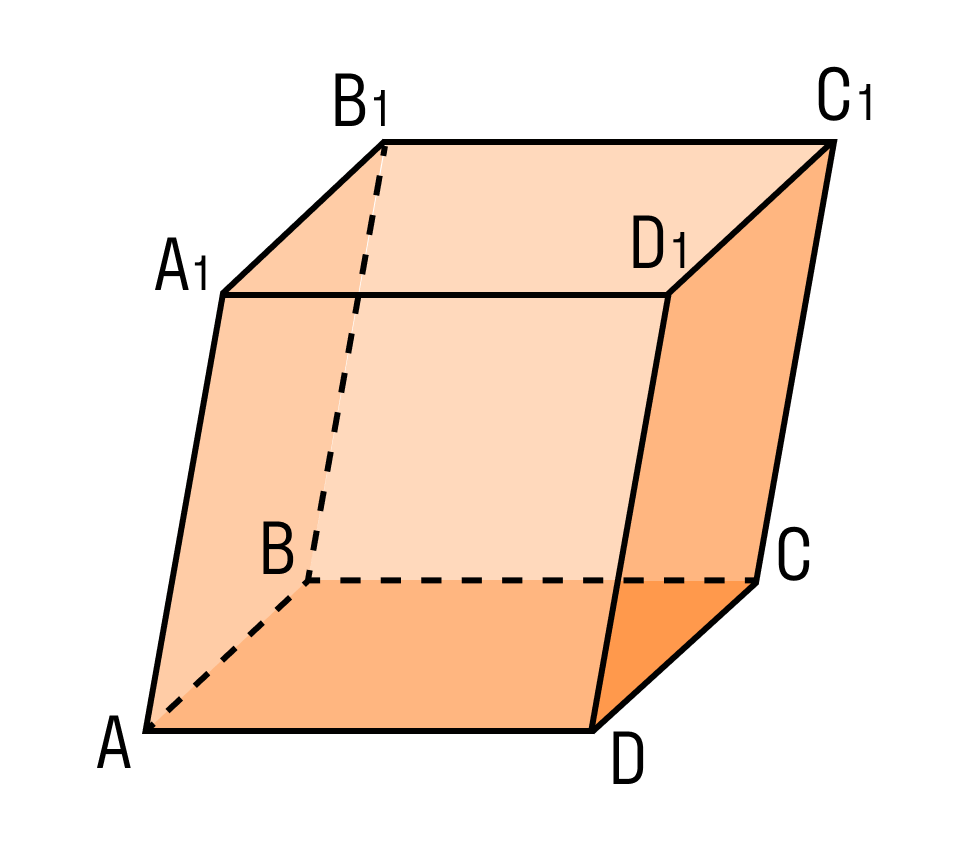
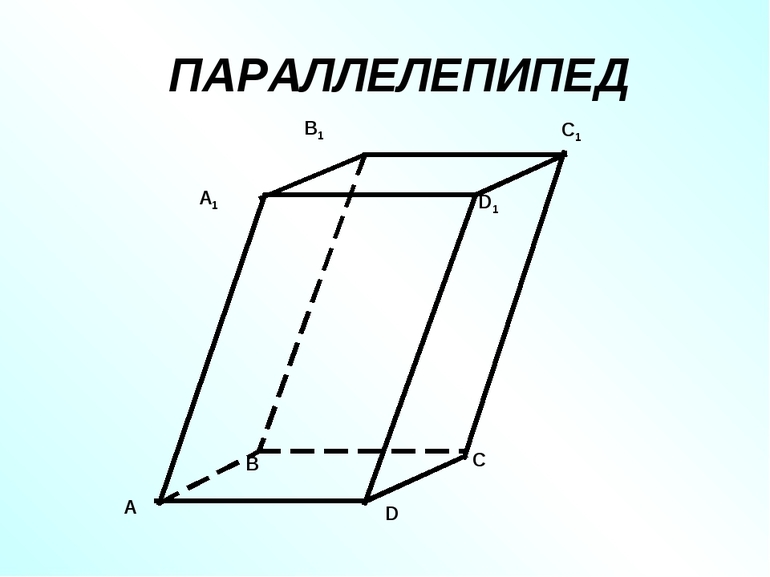
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

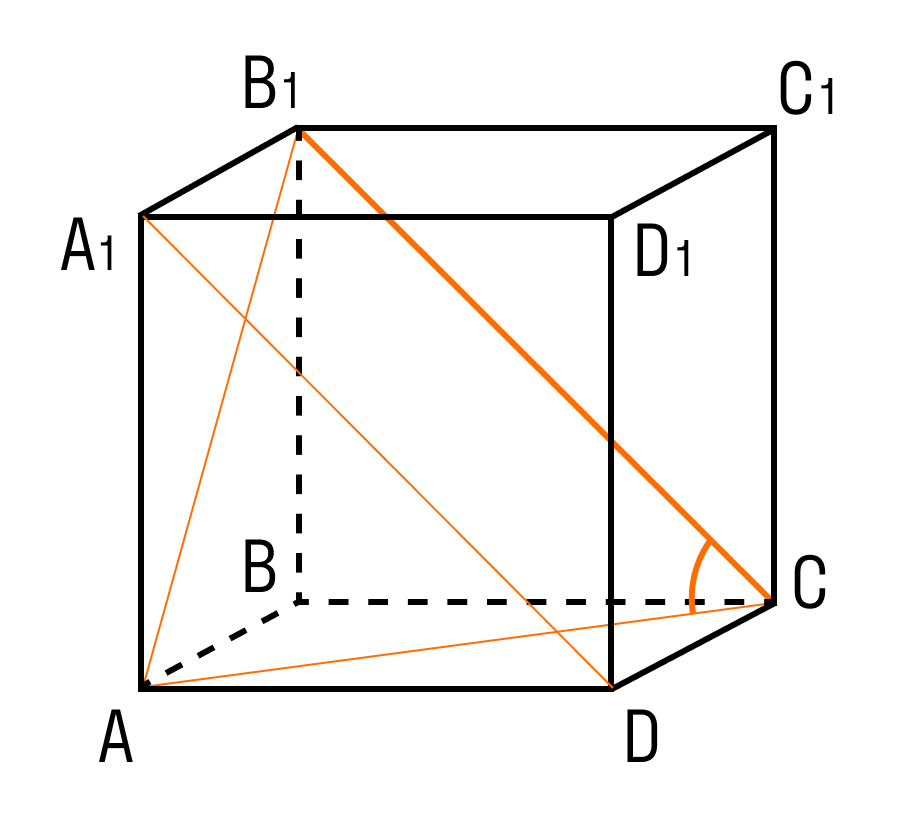
На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

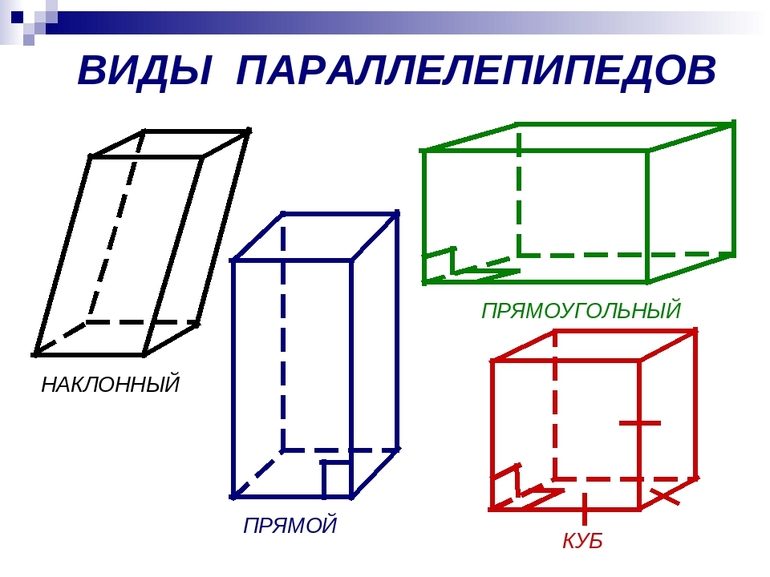
Параллелепипед — это:

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

1. Противолежащие грани параллелепипеда равны и параллельны друг другу.
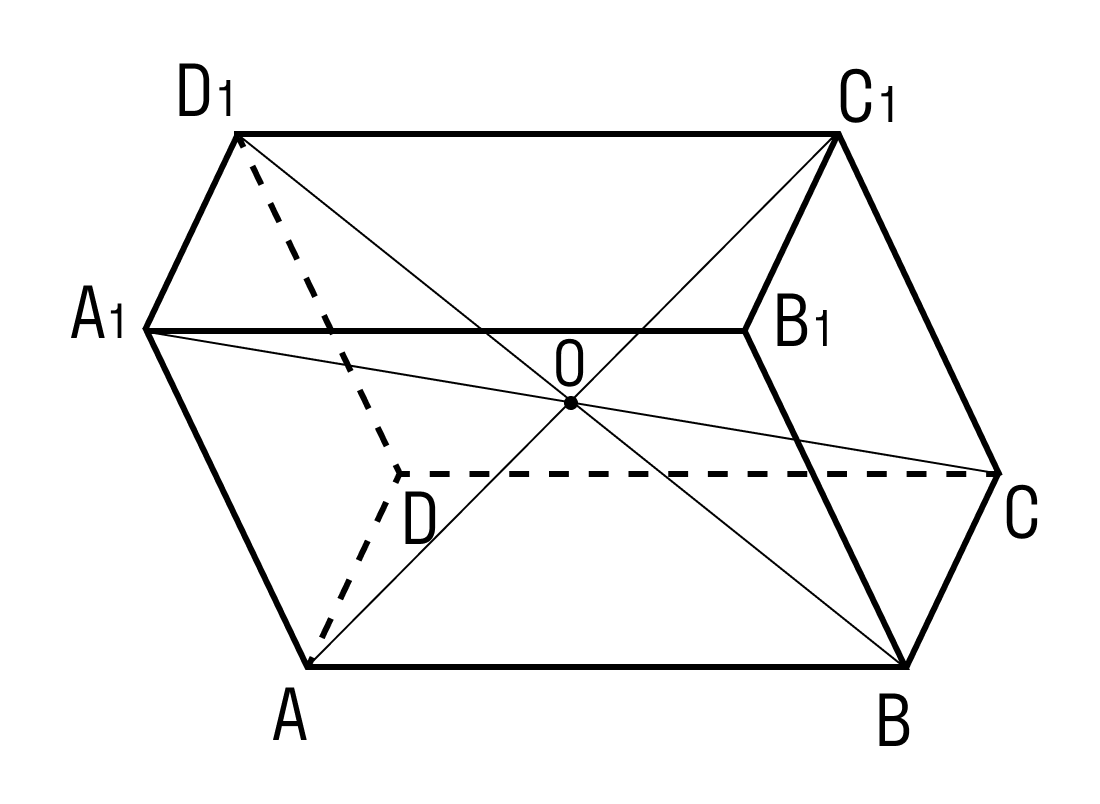
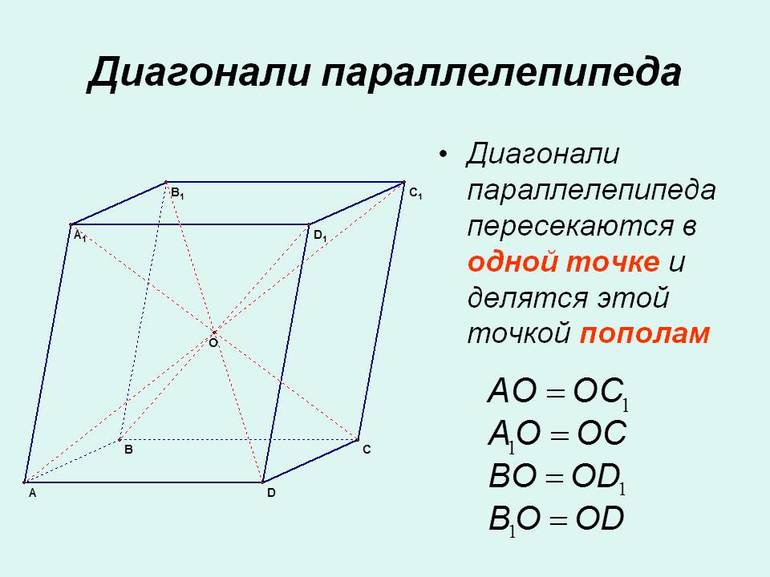
2. Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3. Параллелепипед симметричен относительно середины его диагонали.
4. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

1. Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
2. Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
3. Высота прямого параллелепипеда равна длине бокового ребра.
4. Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
5. Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

• Площадь боковой поверхности прямого параллелепипеда
  Sб = Ро*h
  Ро — периметр основания
  h — высота
• Площадь полной поверхности прямого параллелепипеда
  Sп = Sб+2Sо
  Sо — площадь основания
• Объем прямого параллелепипеда
  V = Sо*h

Видео:Уравнение плоскости. 11 класс.Скачать

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

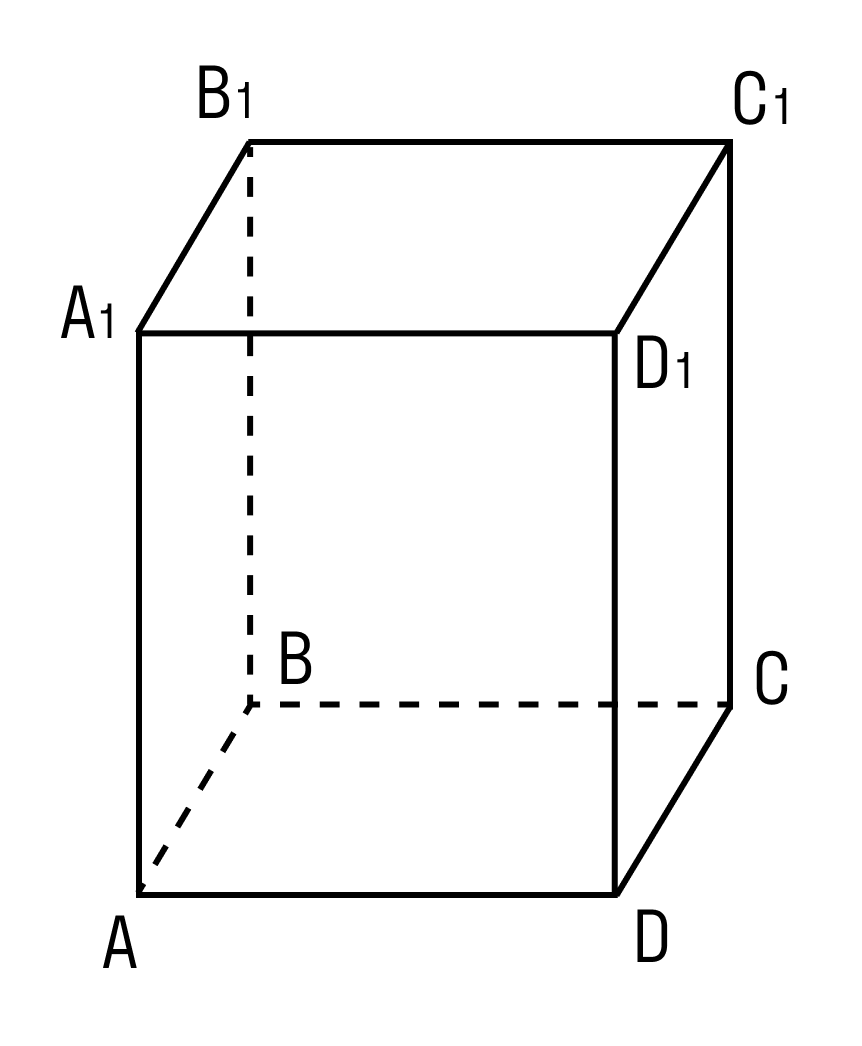
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

1. Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
2. Противолежащие грани параллелепипеда попарно параллельны и равны.
3. Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
4. Диагонали прямоугольного параллелепипеда равны.
5. В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7. Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы прямоугольного параллелепипеда:

• Объем прямоугольного параллелепипеда
  V = a · b · h
  a — длина, b — ширина, h — высота
• Площадь боковой поверхности
  Sбок = Pосн·c=2(a+b)·c
  Pосн — периметр основания, с — боковое ребро
• Площадь поверхности
  Sп.п = 2(ab+bc+ac)

Видео:Уравнения стороны треугольника и медианыСкачать

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

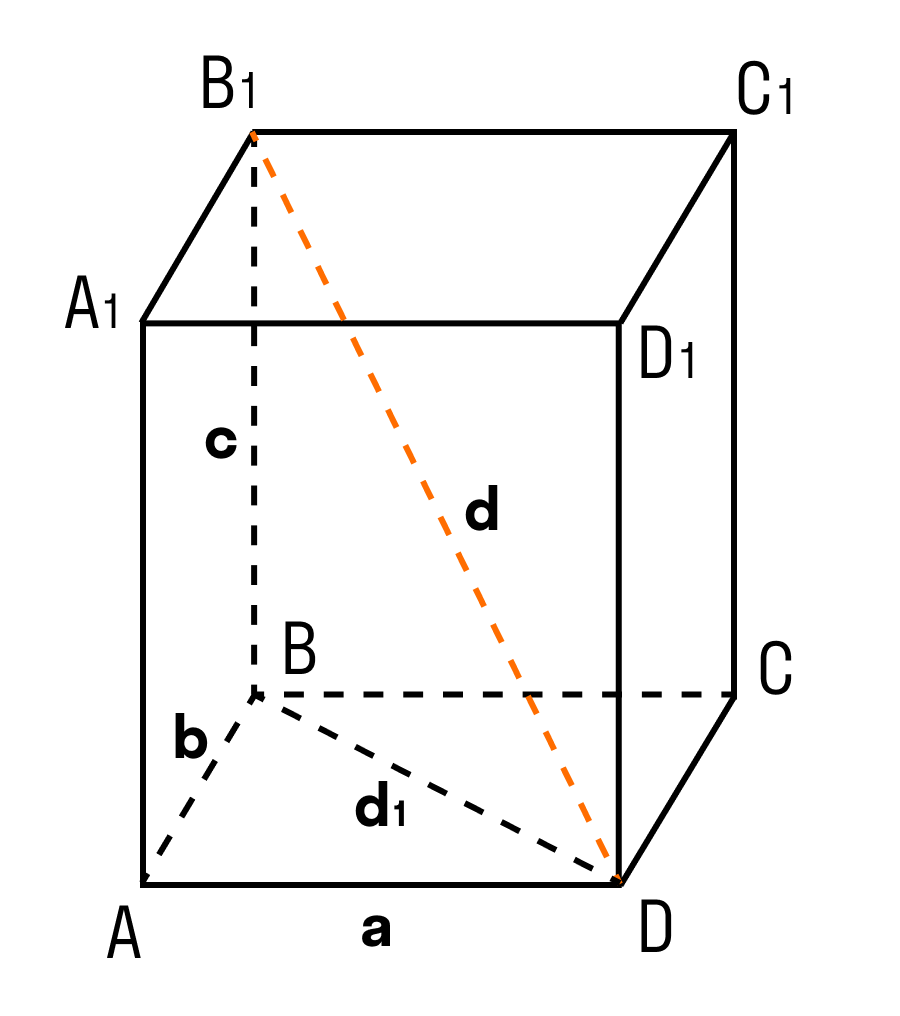
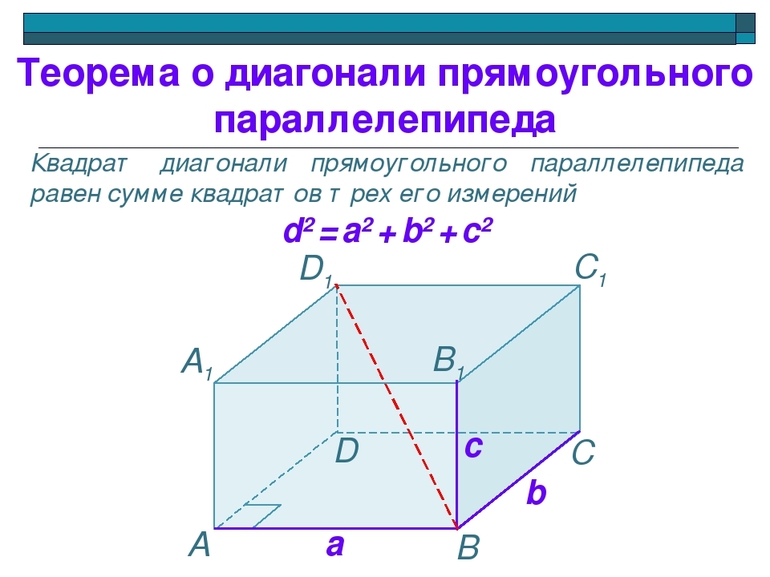
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

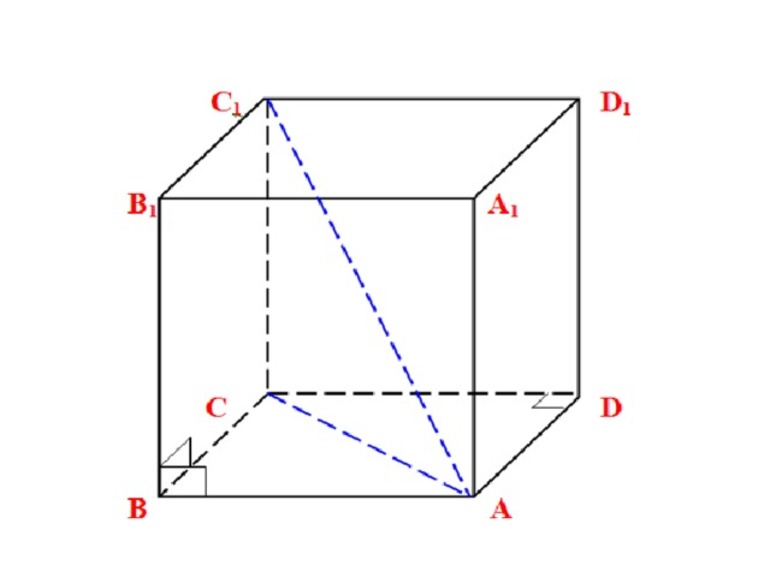
Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = d₁² + c² = a² + b² + c²

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

Видео:Видеоурок "Уравнение плоскости по трем точкам"Скачать

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

1. В кубе 6 граней, каждая грань куба — квадрат.
2. Противолежащие грани параллельны друг другу.
3. Все углы куба, образованные двумя гранями, равны 90°.
4. У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
5. Диагонали куба равны.
6. Диагональ куба в √3 раз больше его ребра.
7. Диагональ грани куба в √2 раза больше длины ребра.

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

• Объем куба через длину ребра a
  V = a3
• Площадь поверхности куба
  S = 6a2
• Периметр куба
  P = 12a

Видео:Стереометрия Параллелепипед Уравнение плоскостиСкачать

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

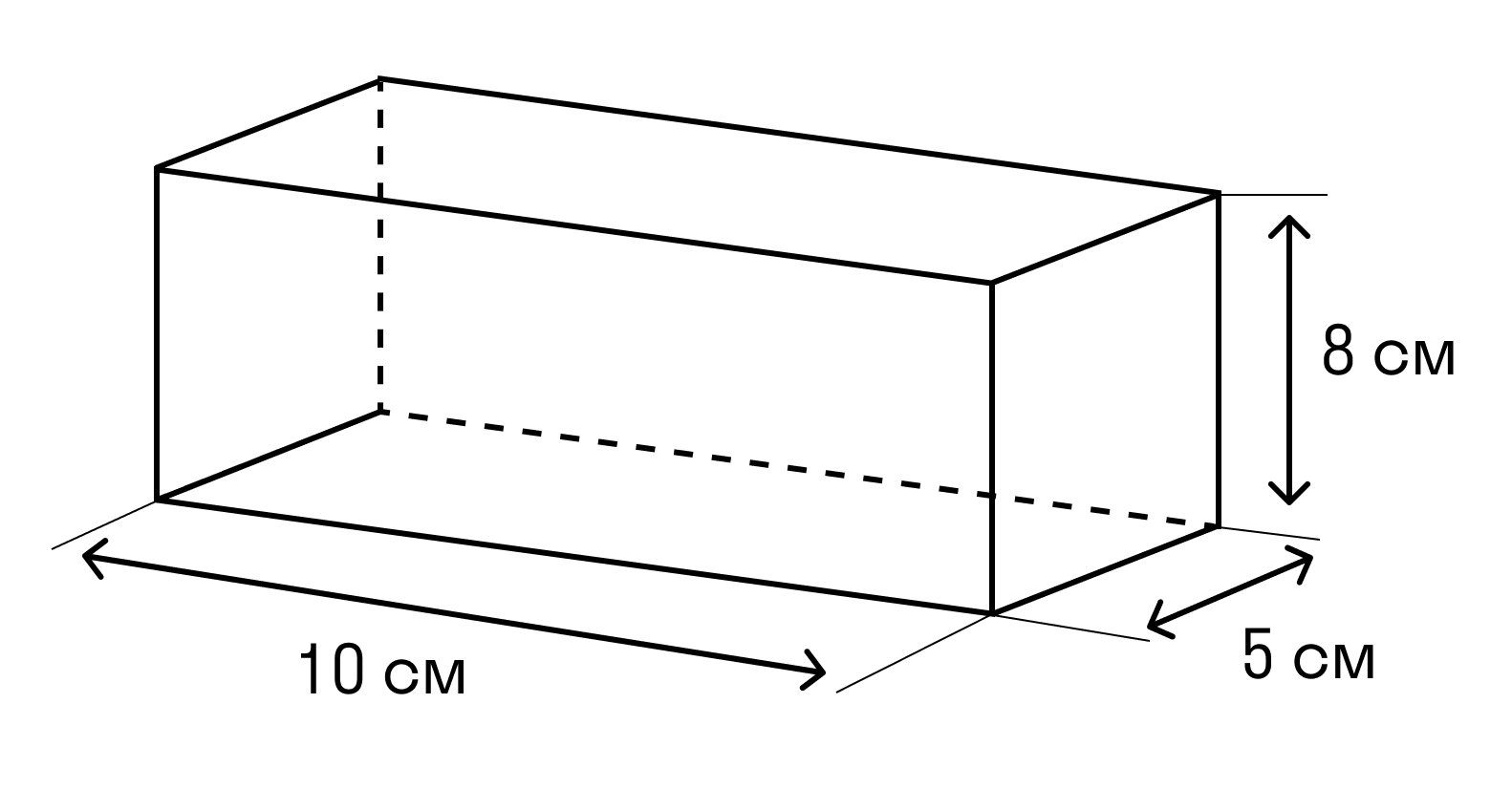
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a — длина, b — ширина, c — высота. Тогда a = 10, b = 5, c = 8.

Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) — сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) — суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) — сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) — сумма длин всех ребер прямоугольного параллелепипеда.

Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X — сумма длин ребер).

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

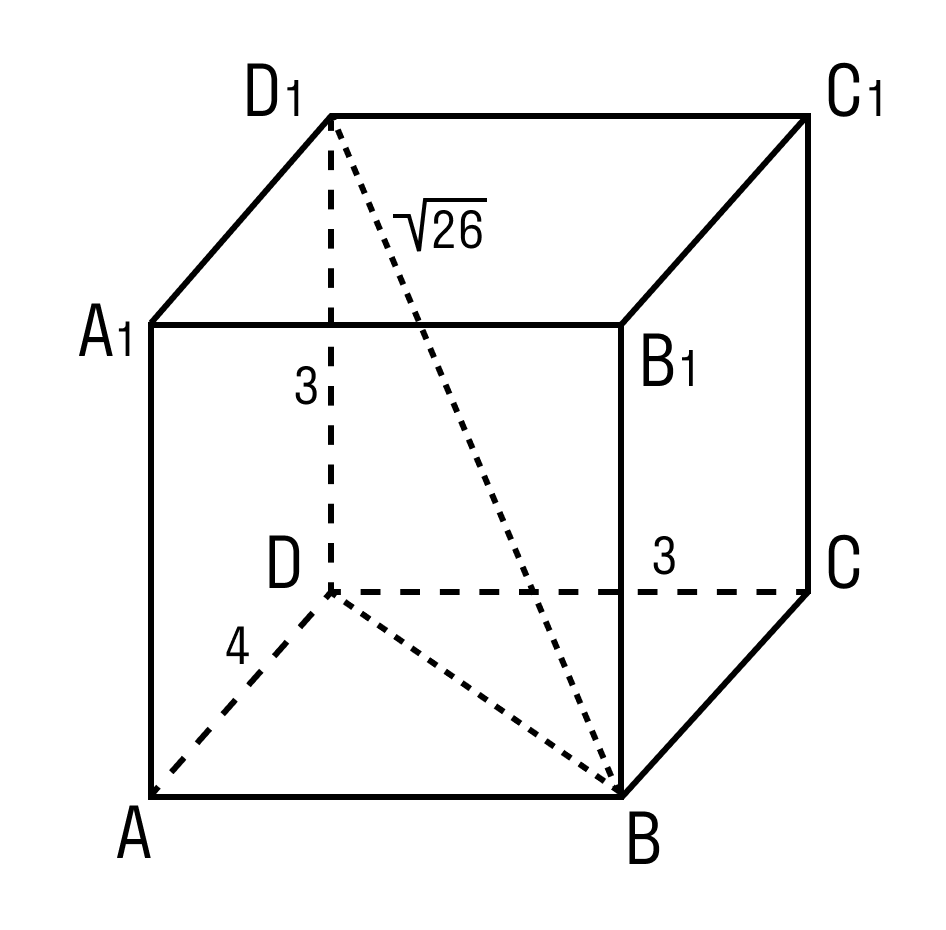
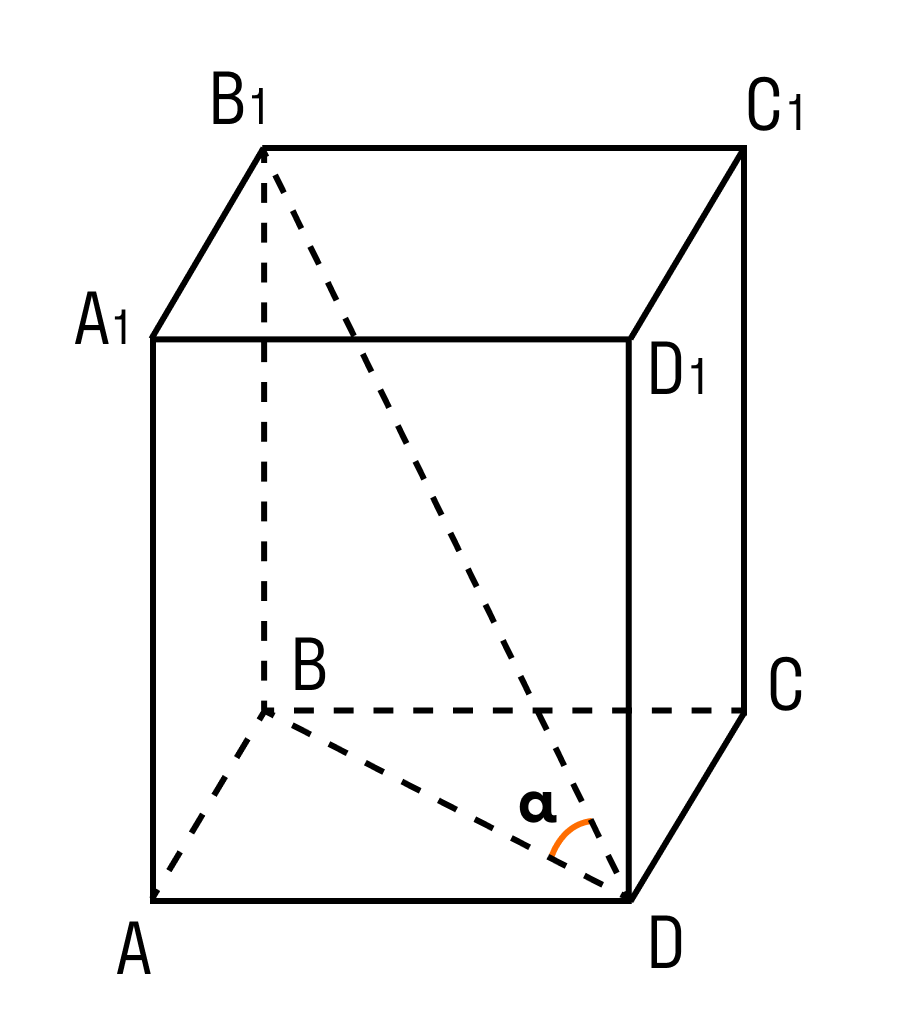
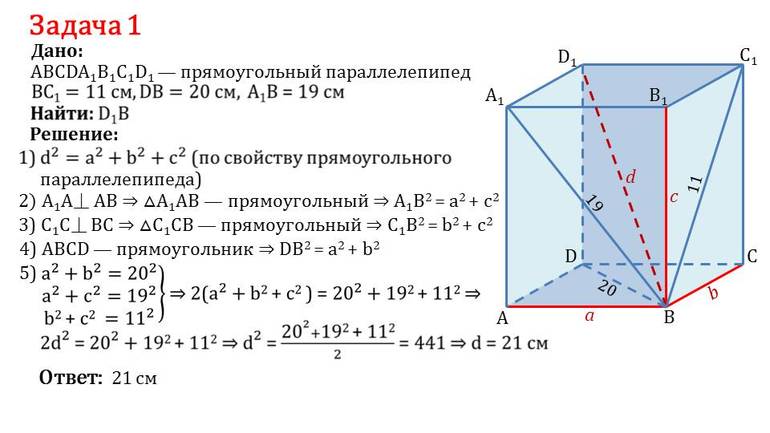
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°.

По теореме Пифагора:
BD₁ 2 = DD₁ 2 + BD 2
BD 2 = BD₁ 2 – DD₁ 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 — AD 2 = (√17)2 — 4 2 = 1
A₁B₁ = AB = 1.

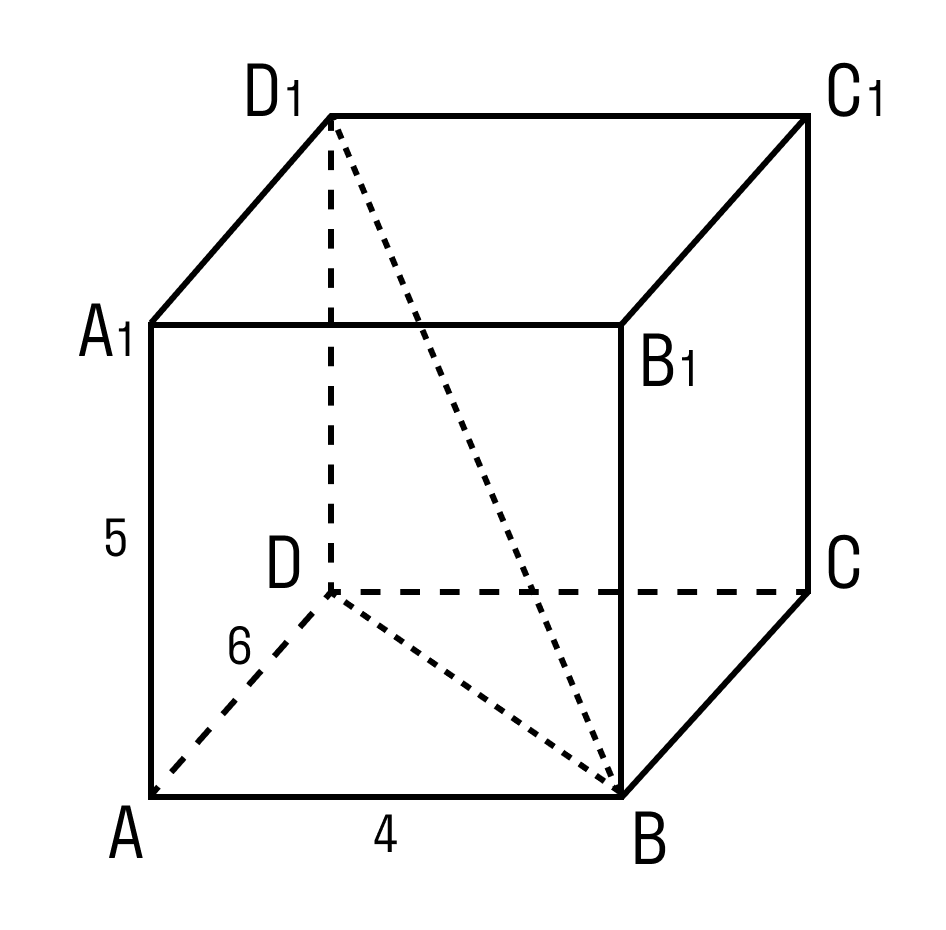
Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77
BD₁ = √77.

Видео:5. Нормальное уравнение плоскости выводСкачать

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

• прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
• параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
• основание прямоугольного параллелепипеда — прямоугольник;
• три измерения прямоугольного параллелепипеда: длина, ширина, высота;
• диагональ параллелепипеда равна сумме квадратов его измерений.

Видео:17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать

Диагональ прямоугольного параллелепипеда — свойства, формулы и примеры

Видео:11 класс, 8 урок, Уравнение плоскостиСкачать

Объект изучения

Прежде чем рассматривать формулу диагонали параллелепипеда, следует изучить подробно, что собой представляет эта фигура. Речь идет о призме, для которой характерны следующие особенности:

• основание представляет собой прямоугольник или квадрат;
• она является прямой, то есть длина любого ее бокового ребра совпадает с высотой.

Как и любой объект в пространстве, параллелепипед состоит из набора элементов. К ним относятся:

1. 8 вершин (точки, в которых пересекаются 3 ребра).
2. 12 ребер (8 из них принадлежат двум основаниям и 4 являются боковыми).
3. 6 граней (2 из них называются основаниями, остальные 4 образуют боковую поверхность). Все грани — прямоугольники. Если они являются квадратами, получается частный случай прямоугольного параллелепипеда — куб.

Фигуру можно получить, если взять плоский четырехугольник с прямыми углами и переместить его вдоль направленного отрезка, который перпендикулярен его плоскости. Длина вектора будет высотой, а исходный прямоугольник — основанием.

С прямоугольным параллелепипедом удобно работать, поскольку его форма идеально соответствует декартовой системе координат. По этой причине существует множество формул, применяя которые можно рассчитать любую геометрическую характеристику объекта.

Видео:Уравнение плоскости через 3 точкиСкачать

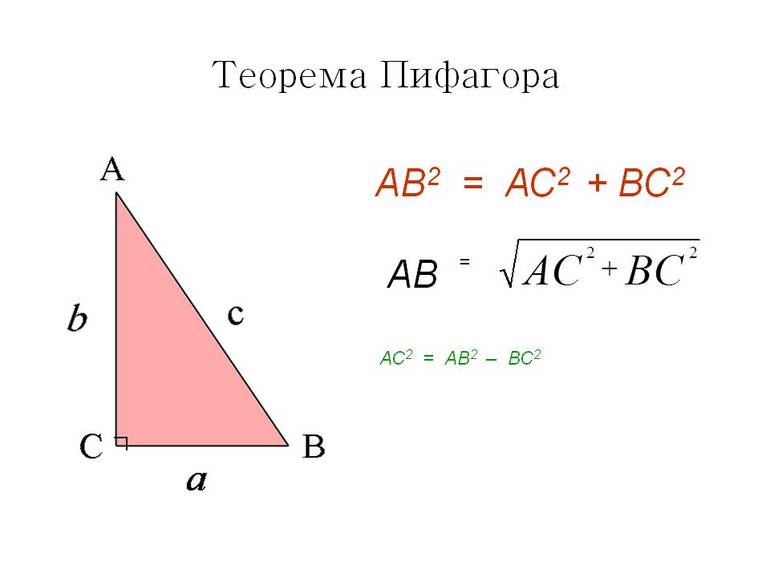
Теорема Пифагора

Теорема справедлива для любого треугольника с прямым углом. Данные исторических архивов свидетельствуют, что греческий философ Пифагор впервые доказал, что при складывании квадратов катетов всегда получается квадрат гипотенузы, то есть стороны, которая лежит против прямого угла.

Теорема Пифагора — полезный геометрический инструмент при расчетах параметров не только треугольников, но и прямоугольников. Если 2 противоположные (несмежные) вершины четырехугольника соединить, получится отрезок, который называется диагональю. Она делит фигуру ровно на 2 половинки, каждая представляет собой треугольник с углом 90 градусов, если исходный четырехугольник является прямоугольным.

Исходя из геометрических построений можно понять, что прямоугольник имеет 2 одинаковые диагонали. Если предположить, что стороны фигуры равны a и b, диагональ c легко рассчитывается по теореме Пифагора: c = (a 2 + b 2 )^0,5.

В случае квадрата получается еще более простая формула: c = a*(2)^0,5.

Видео:2. Уравнение плоскости примеры решения задач #1Скачать

Диагональ параллелепипеда

Особое внимание этому элементу фигуры принято уделять по причине того, что он часто используется для вычисления объема и площади поверхности, совместно с двумя другими линейными параметрами. Прямоугольный параллелепипед определяется тремя линейными характеристиками.

Геометрический элемент

Чтобы построить диагональ параллелепипеда, необходимо рассмотреть его произвольную вершину. Она соединена ребрами с тремя другими. Еще 3 можно соединить с помощью диагоналей граней. В итоге остается лишь одна вершина, которая с исходной соединяется отрезком, проходящим через весь объем фигуры. Этот отрезок называется диагональю параллелепипеда.

Из этих рассуждений несложно понять, сколько диагоналей у параллелепипеда — 4. Их особым свойством является равенство длин. Оно следует из факта симметричности фигуры.

Вывод формулы

Для определения длины диагонали параллелепипеда следует ввести некоторые обозначения. Все вершины одного основания будут A, B, C, D, а их аналоги — A1, B1, C1, D1.

Пусть следует найти диагональ AC1. Дополнительными обозначениями сторон, которые облегчат процедуру вывода формулы, будут:

• a — сторона AB;
• b — сторона AD;
• h — высота параллелепипеда, равна длине сторон AA1, BB1, CC1 и DD1.

Сначала необходимо рассмотреть треугольник ABC, который лежит в плоскости одного из оснований. В нем угол B является прямым, а сторона AC — гипотенуза. Если применить теорему Пифагора, получится следующий результат для длины AC: AC = (a 2 + b 2 )^0,5.

Теперь следует обратить внимание на фигуру, которая ограничена вершинами A, C и C1. Это прямоугольный треугольник, в котором стороны AC и CC1 являются катетами, а диагональ AC1 — гипотенуза. Используя введенные обозначения и снова применяя теорему греческого философа: AC1 = (AC 2 + CC1 2 )^0,5 = (a 2 + b 2 + h 2 )^0,5.

Полученное выражение является искомой формулой для диагонали. Равенство позволяет сделать умозаключение: какие бы стороны ни образовывали фигуру, и какой бы формы она ни была, ее объемная диагональ всегда больше, чем любая из диагоналей грани. Они станут равны только в случае вырождения параллелепипеда в прямоугольник на плоскости (h = 0).

Случай куба

Все рассуждения касательно вывода формулы диагонали параллелепипеда остаются верными для куба. Поскольку фигура обладает высокой симметрией в пространстве, для однозначного определения всех ее параметров необходимо знать лишь одну-единственную сторону квадрата. Пусть это будет a. Общая формула для длины диагонали имеет вид: AC1 = (a 2 + b 2 + h 2 )^0,5.

Если подставить сюда вместо b и h длину стороны a, получается следующее простое равенство: AC1 = a*(3)^0,5.

В кубе его объемная диагональ приблизительно в 1,225 раза больше, чем аналогичный отрезок для грани.

Видео:3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Объем и площадь поверхности

Полученная формула для диагонали не является исключительно теоретической. Ее можно применять для расчета важных для практики величин, например, объема фигуры и площади ее поверхности.

Объем V и площадь поверхности S вычисляются по таким формулам:

V и S однозначно определяются, если знать 3 линейных параметра фигуры. Одним из них может являться длина объемной диагонали, которая зависит от тех же величин, что V и S.

При решении задач, в которых необходимо найти какой-либо объемный параметр или характеристику площади через известные диагонали, потребуется выполнять вычисления с квадратными и кубическими уравнениями.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Косоугольная фигура

Параллелепипед бывает не только прямоугольным, но и наклонным или косоугольным. Основной его отличительной чертой является, что боковое ребро наклонено к плоскости прямоугольного основания под некоторым углом, который отличается от 90 градусов. В таком случае высота фигуры оказывается меньше длины этого ребра.

Наклонный параллелепипед также имеет 4 диагонали в объеме, однако они не всегда имеют одинаковую длину. В этом случае не существует какой-либо конкретной формулы для расчета длины. Для решения подобных сложных задач можно воспользоваться двумя методами:

1. Если известны двугранные углы, определяющие наклоны боковых граней по отношению к основаниям, можно воспользоваться знаниями тригонометрии для вычисления диагоналей. Метод является достаточно сложным, поскольку требует знания других теорем.
2. Если известны координаты вершин параллелепипеда в прямоугольной декартовой системе координат, можно воспользоваться достаточно простым методом вычисления длин отрезков. Для этого следует найти разности соответствующих координат выбранных вершин, возвести каждую из разностей в квадрат, взять сумму полученных трех слагаемых и возвести ее в степень ½. Это обычный метод нахождения длины отрезка по координатам его концов.

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Пример решения задачи

Пусть дан прямоугольный параллелепипед, основаниями которого являются прямоугольники ABCD и A1B1C1D1. Известны следующие его параметры:

• диагональ грани бокового четырехугольника AD1 = 5 см;
• высота AA1 = 4 см;
• объем V = 64 см.

Необходимо найти объемную диагональ этой фигуры.

Пусть AB = a, AD = b, AA1 = h. Для решения задачи сначала необходимо выписать известные равенства, выраженные через параметры a, b, h:

• V = a*b*h = 64;
• AD1 2 = a 2 + h 2 = 5 2 = 25.

Из выражения для AD1 и h = 4 см получается значение a = 3 см. При подстановке его в формулу для V, получается значение стороны b = 5,33 см.

Теперь остается подставить значения a, b, h и рассчитать по формуле значение AC1. Получается число: AC1 = (a 2 + b 2 + h 2 )^0,5 = (3 2 + 5,33 2 + 4 2 )^0,5 = 7,31 см.

Таким образом, все диагонали прямоугольного параллелепипеда равны между собой. Для определения их длины необходимо сложить квадраты длин всех сторон объемной фигуры и взять квадратный корень от полученной суммы.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Диагональ прямоугольного параллелепипеда

Параллелепипед — это частный случай призмы, в основании которой лежит прямоугольник с длиной a и шириной b. Двигаясь по вертикальной или наклонной оси на определенную высоту c, данный прямоугольник создает объемное тело, именуемое параллелепипедом.

Параллелепипед по определению может быть наклонным или прямым, то есть угол между высотой и прямоугольником в основании варьируется от 0 до 90 градусов. Прямой параллелепипед имеет в качестве граней исключительно прямоугольники, и даже иногда квадрат (в основании), поэтому решение задач с его участием значительно облегчено. В случае с наклонным параллелепипедом в формулах необходимо учитывать, что боковой гранью является параллелограмм, строение которого зависит также от угла его наклона.

Помимо трех вышеуказанных параметров параллелепипеда — длины, ширины высоты, являющихся его ребрами, в данном теле можно также провести еще несколько отрезков, соединяющих его вершины. Как и в геометрических фигурах на плоскости, линии, проходящие внутри основного каркаса через вершины, называются диагоналями. Диагонали боковых граней прямоугольного параллелепипеда идентичны диагоналям прямоугольников, которыми представлены грани — их, соответственно, можно вычислить, используя подходящий онлайн калькулятор для прямоугольников.

Другое дело — диагональ, проходящая не по внешней поверхности прямоугольного параллелепипеда, а сквозь него, соединяя противоположные вершины верхнего и нижнего оснований. При этом, какая именно пара противоположных вершин соединена, не имеет значения для расчетов, так как если рассмотреть сечения, можно увидеть, что обе диагонали параллелепипеда идентичны и найти их можно одним и тем же способом.

Итак, для того чтобы вывести формулу диагонали через длину, ширину и высоту, необходимо заключить диагональ в плоскую геометрическую фигуру, свойства которой можно будет использовать. Для этого в любом основании — верхнем или нижнем, проводится диагональ, которая образует с диагональю параллелепипеда и боковым ребром (высотой) прямоугольный треугольник. Применив одну лишь теорему Пифагора, можно найти диагональ основания через ширину и длину,а затем диагональ прямоугольного параллелепипеда, добавив в расчеты высоту.

Используя последнюю и предпоследнюю формулу, можно также успешно найти длину, ширину или высоту прямоугольного параллелепипеда, имея в заданных условиях три параметра из четырех, включая диагональ параллелепипеда. Например:

🎥 Видео

Лекция 25. Виды уравнений плоскости в пространстве.Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать