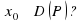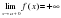Как построить график функции?
С каждым днём всё больше и больше развиваются технологии и теперь уже неизбежно их внедрение в науку. В этой статье рассмотрим, как технологии внедряются в математику, и в особенности, остановимся на рисовании графиков с помощью специальной программы Advanced Grapher.
В начале хочу заметить, что также очень бурно развивается Интернет технологии, и сейчас легко можно нарисовать график функции одной переменной прямо на сайте, это очень удобно и быстро.
Но вернёмся к программе Advanced Grapher, с её помощью можно строить графики не только функций одной переменной, но и:
- параметрических функций,
- функций двух переменных,
- неравенств,
- функций в полярной системе координат,
- а также, графики заданные с помощью таблицы.
Версия 2.2 этой программы совершенно бесплатная для некоммерческих целей, поэтому мы можем легко ею пользоваться. Устанавливается она также очень просто, запускаем setup-файл, который скачали с Интернета, только не забываем указать, что программа для не коммерческих целей, а далее всё без изменений.
И так, сразу рассмотрим, как построить график функции. Нажимаем вкладку «Графики» в верхнем меню и выбираем пункт «Добавить график» (можно ещё просто нажать на кнопку «Добавить график», которая есть среди кнопок, что расположены под Главным меню или нажать правой клавишей мыши в окне «Список графиков» и выбрать пункт «Добавить график»).
После чего, перед нами появится окно, где мы можем выбрать вид функции, то есть, как она будет задана (с одной переменной или двумя, или может с параметром и т.д.). Выбрав вид функции, вводим в поле «Формула» саму функцию. Также ещё можем выбрать толщину линии её стиль и цвет (это удобно, если на одном рисунке несколько разных графиков). Ещё можете заполнить поле «Описание» (это не обязательно), то есть дать имя своёму графику.
После того, как всё это сделали, нажимаем кнопку «ОК» и видим свой график. Сразу в правом окне «Список графиков» появится наш график, если надо изменить какие-то его свойства, то кликаем два раза по нему и вновь появится предыдущее окно, но уже с указанными свойствами этого графика и там всё можно изменить. Если надо удалить конкретный график, то ищем его в списке и нажимаем правой клавишей мыши и в появившемся списке выбираем пункт «Удалить». Или можно просто снять галочку, что стоит напротив этой функции, тогда график исчезнет, а если он опять понадобится, то поставить галочку снова.
Кроме этого вы можете сделать много других полезных вычислений связанных с графиками, с ними вы можете ознакомиться во вкладке «Вычисления» главного меню. Там вы можете:
- Исследовать функцию, то есть найти нули и экстремумы функции;
- Вычислить точки пересечения функций;
- Найти производную функции и нарисовать её график;
- Найти касательную или нормаль функции и нарисовать её график;
- А с помощью интегрирования, вычислить площадь фигуры, что расположена между функциями, и нарисовать её график.
Всё это делается очень просто, после того, как вы нарисовали график, вы выбираете соответствующий пункт в меню, потом в появившемся окне выбираете ту функцию (или функции) для которой вам надо найти вышеуказанные характеристики (или характеристику). Если это надо, то изменяете нужные параметры, и получаете результат. Там всё интуитивно понятно.
Часто бывает нужно, что бы на графике была сетка, для этого вы клацаете правой клавишей мыши по окну, с нарисованными графиками, и ставите галочки около пунктов «Вертикальные и Горизонтальные линии сетки». Там же вы можете поставить галочку напротив пункта «Легенда». Легенда – это список нарисованных графиков. Ещё там вы увидите пункт «Свойства документа», можете зайти и ознакомится с ними, если вам что-то понабиться, то измените там.
Ну и на конец, если вам надо увеличить или уменьшить масштаб по главных осях, вы можете пользоваться не только «Свойствами документа» (где можно указать числа максимума и минимума), но и соответствующими кнопками, что расположены под главным меню.
Для того, что бы сохранить ваш график в виде рисунка (после того, как всё нарисовали) выбираем вкладку «Файл» и там пункт «Сохранить как рисунок». Там выбираем формат и место, где сохранить этот рисунок (кнопка «Обзор»), после чего нажимаем «ОК».
Видео:Advanced Grapher - программа для построения графиковСкачать

Методическая разработка открытого занятия по математике Асимптоты графика функции.Нахождение асимптот.
Государственное образовательное учреждение
среднего профессионального образования
Луганской Народной Республики
«Луганский строительный колледж»
по дисциплине «Математика» на тему:
«Асимптоты графика функции. Нахождение асимптот»
по специальности 38.02.01 «Экономика и бухгалтерский учёт (по отраслям).
категории Еськова Л.В.
Познакомить студентов с определением асимптоты графика функции, видами асимптот и методами их нахождения, обобщить и систематизировать знания определения предела функции и закрепить умения нахождения пределов функции;
Развивать аналитическое мышление, умение проводить аналогии, сравнивать и обобщать;
Воспитывать аккуратность, графическую культуру, усидчивость и настойчивость в достижении результата.
Материально-техническое обеспечение и дидактические средства, ТСО: доска, ПК, мультимедийная установка , программное обеспечение ( Windows 7, Advanced Grapher ), раздаточный материал .
Высшая математика. (В 3-х томах) Бугров Я.С., Никольский С.М.Т.2. Дифференциальное и интегральное исчисление. М., Дрофа, 2004. – 512 с.
Высшая математика. (В 3-х томах) Бугров Я.С., Никольский С.М. Т.3. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М., Дрофа, 2004. — 512 с.
Грибанов В.М., Крамарь Н.М., Швед О.П. Высшая математика. Курс лекций (часть I , II , III ).-Луганск: Изд-во ВНУ им. В.Даля, 2003.
Н.Д. Владыкина, А.И. Ермаков, С.С. Курчанова, Г.И. Хмеленко. – Луганск: изд. Восточноукр. Нац. ун-та им. В. Даля, 2002. — 100 стр. Методические указания по курсу высшей математики. Часть 1.
Роева Т.Г., Хроленко Н.Ф. Алгебра в таблицах, 10-11 класс: Учеб. пособие.- Х.: Издательская группа «Академия».
Приветствие. Сообщение темы и цели занятия.
Мотивация учебной деятельности.
Сегодня на занятии мы знакомимся с очень важным понятием математического анализа асимптотами графика функции. Вы уже умеете проводить исследование функции и построение графика с помощью производной, находить промежутка монотонности, экстремумы функции и промежутки выпуклости и вогнутости, точки перегиба. Но как ведет себя функция в точках разрыва, как построить ее график вблизи этих точек. Ответы на эти и другие вопросы мы должны узнать на этом занятии. Итак, запишите в тетради план занятия:
Асимптоты графика функции.
Использование программного обеспечения для построения асимптот.
Нахождение асимптот графиков функции.
2. Актуализация опорных знаний.
Так как нахождение асимптот напрямую связано с вычислением пределов функции, то давайте повторим основные правила нахождения пределов.
Как найти предел многочлена при
Как найти предел дробно — рациональной функции: при , если
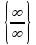
Как избавиться от неопределенности или ?
Назовите первый замечательный предел.
Изложение нового материала.
При исследовании графика функции при или в окрестности точек разрыва второго рода, часто оказывается, что график функции сколько угодно близко приближается к некоторой прямой. Такие прямые называются асимптотами графика функции.
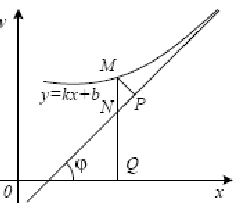
Если график функции имеет бесконечные ветви, то у графика функции возможно есть асимптоты. Асимптоты — это прямые, к которым неограниченно приближается кривая графика функции при стремлении аргумента функции к бесконечности (рис. 1). Прежде чем приступить к построению графика функции, нужно найти все вертикальные и наклонные (горизонтальные) асимптоты, если они существуют.
Определение Прямая L называется асимптотой графика функции , если расстояние d от переменной точки графика до прямой L стремится к нулю при удалении точки М по кривой в бесконечность.
Определение. Прямая называется асимптотой графика функции при , если .
Существует три вида асимптот: горизонтальные, вертикальные и наклонные.
Определение. Прямая называется вертикальной асимптотой графика функции , если хотя бы один из пределов (правый предел) или (левый предел) равняется или , т.е. (рис. 2).
Очевидно, прямая не может быть вертикальной асимптотой, если функция непрерывная в точке , потому что в этом случае . Итак, вертикальные асимптоты следует искать в точках разрыва функции или на концах ее области определения , если и — конечные числа.
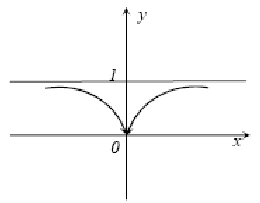
Определение. Прямая называется горизонтальной асимптотой графика функции , если существуют конечные пределы или (рис. 3).
Если конечен только один из пределов или , то функция имеет лишь одну правостороннюю или левостороннюю горизонтальную асимптоту. Если = =, то говорят просто о горизонтальной асимптоте. В том в случае, когда , то функция не имеет соответствующей горизонтальной асимптоты, но может иметь наклонную асимптоту.
Определение . Прямая называется наклонной асимптотой графика функции , если функция определена при достаточно больших и существуют конечные пределы (рис. 4).
Если, хотя бы один из пределов не существует или равен бесконечности, то график исследуемой функции не имеет соответствующей наклонной асимптоты.
Использование программного обеспечения Advanced Grapher к построению асимптот графика функции.
Advanced Grapher является мощным программным графическим обеспечением. Вы можете использовать его для построения графиков функций, уравнений, неравенств и таблиц.
Программа также позволяет выполнять построение кривых, анализировать
функции, находить точки пересечения графиков с осями координат, касательные и нормали графиков и многое другое.
Вы можете указать цвет, стиль и ширину линий, стиль и размер точек, построение по линиям и (или) точкам, стиль затенения (для неровности) для каждого графика. Вы также можете изменить дополнительные свойства графиков в зависимости от типа графика, например, количество точек, построение интервалов, сортировка (для таблиц), и т.д. Программа имеет многоязычный интерфейс (рис. 5).
Нахождение асимптот графика функции.
Пример № 1. Найти вертикальные и горизонтальные асимптоты графика функции
Очевидно, что область определения функции . Вертикальные асимптоты ищем в точках разрыва функции. Таким образом, прямая может быть вертикальной асимптотой данной функции. Вычисляем границы
и Из этого вытекает, что прямая является вертикальной асимптотой графика исследуемой функции.
Найдем горизонтальную асимптоту . Вычисляем пределы,
используя правило Лопиталя. Получим
=. Поэтому, что = =, то график функции имеет только одну горизонтальную асимптоту. С помощью программы Advanced Grapher легко построить график функции и асимптоты (рис. 6)
Пример № 2. Найти асимптоты графика функции
Очевидно, что график функции не имеет ни вертикальных асимптота (нет точек разрыва), ни горизонтальных асимптот.
Найдем наклонную асимптоту. Вычисляем границы и , .
Таким образом, правая наклонная асимптота имеет вид . Очевидно, что левая наклонная асимптота будет иметь те же значения, что и правая, а это значит, что график исследуемой функции имеет одну наклонную асимптоту. Что и подтверждает построение в программе Advanced Grapher (рис.7).
Перейдем к практической части нашего занятия – решению примеров.
Закрепление изложенного материала.
Пример № 1. Найти асимптоты графика функции
Решение : Исследуем функцию сначала на наличие наклонной асимптоты. Найдем и пределы
Прямая является наклонной асимптотой графика функции при , а также прямая также является асимптотой графика функции при . Проверим наличие вертикальных асимптот.
Точка является точкой разрыва функции. Найдем предел
, он равен бесконечности, поэтому прямая (ось ) является вертикальной асимптотой.
Построение асимптот видим на рисунке (рис 8).
Пример № 2. Найти асимптоты графика функции .
Решение : Найдем пределы и
Подставляя найденные значения и в уравнение наклонной асимптоты, получим уравнение . Точка это точка разрыва функции. Найдём предел , поэтому прямая является вертикальной асимптотой.
График в программе Advanced Grapher наглядно демонстрирует построение асимптот (рис. 9).
Пример № 3. Найти асимптоты графика функции .
, подставляя значение , получим .
Подставляя найденные значения и в уравнение наклонной асимптоты, получим уравнение . Точка это точка разрыва функции.
Найдем предел , поэтому прямая является вертикальной асимптотой.
Построение асимптот видим на рисунке (рис.10).
Пример № 4. Найти асимптоты графика функции .
Решение : Найдем пределы Найдем Таким образом прямая является асимптотой графика данной функции при .
Аналогично прямая также является асимптотой графика данной функции при .
Пример № 5. Найти асимптоты графика функции .
Рассмотрим точки и . Это точки разрыва функции. Имеем . Поэтому прямые и являются вертикальными асимптотами графика данной функции (рис.12). Найдем предел , поэтому ось является горизонтальной асимптотой.
Подведение итогов. Домашнее задание.
Итак, сегодня мы ознакомились с определением асимптот графика функции, видами асимптот и способом их вычисления с помощью пределов. Рассмотрели некоторые примеры нахождения асимптота графика функции.
Проработать материал учебника Высшая математика. Бугров Я.С., Никольский С.М.Т.2 § 4.20, с. 212-215. Найти асимптоты графиков функции: 1). ; 2). .
Видео:Пределы №6 Нахождение асимптот графиков функцийСкачать

Асимптоты графика функции. Нахождение асимптот.
Методическая разработка занятия дисциплине «Математика» на тему:
«Асимптоты графика функции. Нахождение асимптот» по специальности 38.02.01 «Экономика и бухгалтерский учёт (по отраслям) выполнена в соответствии с рабочей программой.
Организация-разработчик: ГОУ СПО ЛНР «Луганский строительный колледж».
Разработчик: Еськова Лариса Викторовна, преподаватель – методист высшей квалификационной категории.
Аннотация: данная методическая разработка помогает в доступной форме с использованием компьютерных технологий обучения ознакомить студентов с понятием асимптоты графика функции, видами асимптот и методами их нахождения. Использование графического редактора позволяет наглядно продемонстрировать правильность найденного решения или же найти допущенную ошибку.
Формы организации познавательной деятельности:
*метод коллективного взаимодействия;
*метод контроля и оценки
Просмотр содержимого документа
«Асимптоты графика функции. Нахождение асимптот.»
Государственное образовательное учреждение
среднего профессионального образования
Луганской Народной Республики
«Луганский строительный колледж»
занятия по дисциплине «Математика» на тему:
«Асимптоты графика функции. Нахождение асимптот»
специальностm 38.02.01 «Экономика и бухгалтерский учёт (по отраслям)».
категории Еськова Л.В.
Познакомить с определением асимптоты графика функции, видами асимптот и методами их нахождения, обобщить и систематизировать знания определения предела функции и закрепить умения нахождения пределов функции;
Развивать аналитическое мышление, умение проводить аналогии, сравнивать и обобщать;
Воспитывать аккуратность, графическую культуру, усидчивость и настойчивость в достижении результата.
Материально-техническое обеспечение и дидактические средства, ТСО: доска, ПК, мультимедийная установка, программное обеспечение (Windows 7, Advanced Grapher), раздаточный материал.
Бугров Я.С., Никольский С.М. Высшая математика. (В 3-х томах)Т.2. Дифференциальное и интегральное исчисление. М., Дрофа, 2004. – 512 с.
Бугров Я.С., Никольский С.М. Высшая математика. (В 3-х томах) Т.3. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного пер еменного. М., Дрофа, 2004. — 512 с.
Грибанов В.М., Крамарь Н.М., Швед О.П. Высшая математика. Курс лекций (часть I, II, III).-Луганск: Изд-во ВНУ им. В.Даля, 2003.
Н.Д. Владыкина, А.И. Ермаков, С.С. Курчанова, Г.И. Хмеленко. – Луганск: изд. Восточноукр. Нац. ун-та им. В. Даля, 2002. — 100 стр. Методические указания по курсу высшей математики. Часть 1.
Роева Т.Г., Хроленко Н.Ф. Алгебра в таблицах, 10-11 класс: Учеб. пособие.- Х.: Издательская группа «Академия».
Приветствие. Сообщение темы и цели занятия.
Мотивация учебной деятельности.
Сегодня на занятии мы знакомимся с очень важным понятием математического анализа асимптотами графика функции. Вы уже умеете проводить исследование функции и построение графика с помощью производной, находить промежутка монотонности, экстремумы функции и промежутки выпуклости и вогнутости, точки перегиба. Но как ведет себя функция в точках разрыва, как построить ее график вблизи этих точек. Ответы на эти и другие вопросы мы должны узнать на этом занятии. Итак запишите в тетради план занятия:
Асимптоты графика функции.
Использование программного обеспечения для построения асимптот.
Нахождение асимптот графиков функции.
2. Актуализация опорных знаний.
Так как нахождение асимптот напрямую связано с вычислением пределов функции, то давайте повторим основные правила нахождения пределов.
Как найти предел многочлена 
Как найти предел дробно — рациональной функции: 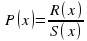
Как избавиться от неопределенности 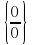
Назовите первый замечательный предел.
Изложение нового материала.
При исследовании графика функции при 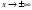
Если график функции 
Определение Прямая L называется асимптотой графика функции 
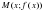
Определение. Прямая 

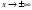
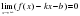
Существует три вида асимптот: горизонтальные, вертикальные и наклонные.
Вертикальная асимптота 
Определение. Прямая 



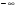
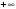
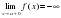
Очевидно, прямая 






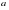
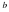
Горизонтальная асимптота 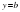
Определение. Прямая 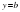


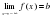
Если конечен только один из пределов 
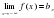


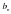
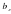
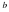
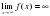
Наклонная асимптота
Определение. Прямая 

Если, хотя бы один из пределов не существует или равен бесконечности, то график исследуемой функции не имеет соответствующей наклонной асимптоты.
Использование программного обеспечения Advanced Grapher к построению асимптот графика функции.
Advanced Grapher является мощным программным графическим обеспечением. Вы можете использовать его для построения графиков функций, уравнений, неравенств и таблиц.
Программа также позволяет выполнять построение кривых, анализировать
💥 Видео
Асимптоты графика функции. Практика. Пример 1.Скачать

Асимптоты функции. 10 класс.Скачать

Асимптоты к графику функций. 10 классСкачать

Строим графики математических функций с помощью Advanced GrapherСкачать

Исследование функции. Часть 4. Асимптоты графика функцииСкачать

Математический анализ, 15 урок, АссимптотыСкачать

Общая схема исследования функции и построение ее графикаСкачать

Найти интервалы выпуклости и точки перегиба графика функцииСкачать

График функции с модулемСкачать

Асимптоты функции. Горизонтальная асимптота. 10 класс.Скачать

Асимптоты функции. Наклонная асимптота. 10 класс.Скачать

Асимптоты графика функции. Опорный конспект (шпаргалка).Скачать

Асимптоты графика функции (часть 4). Высшая математика.Скачать

Graph построение графиковСкачать

Исследование функции. Асимптоты графика от bezbotvyСкачать

14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Исследование функции, построение графикаСкачать

Нахождение асимптоты параметрически заданной функции.Скачать