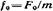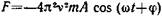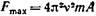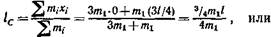Периодическое движение объекта, частицы или количества через равные промежутки времени относительно среднего положения известно как колебание.
Когда тело колеблется, оно включает как линейное, так и угловое смещение, это угловое смещение известно как угловая частота колебаний. В физике есть также другие термины для угловой частоты, такие как угловая скорость и орбитальная частота.
Угловая частота — это скалярная мера углового смещения колеблющейся частицы. Для синусоидальных волн это называется скоростью изменения фазы. Когда мяч, привязанный к веревке, вращается по кругу, скорость, с которой он совершает одно колебание на 360 градусов, называется угловой частотой.
- Формула угловой частоты колебаний
- Угловая частота колебательной пружины
- Угловая частота колебательного маятника
- Угловая частота колебаний объекта
- Как найти угловую частоту колебаний
- Часто задаваемые вопросы (FAQ)
- Какая угловая частота колебаний?
- Как угловая частота связана с периодом времени?
- Какая единица измерения угловой частоты?
- Угловая частота совпадает с частотой?
- МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ Основные формулы
- Какова частота напряжения тока, а точнее частота электрического тока. Частота в электротехнике
- Период и частота гармонических колебаний
- ⓘ Энциклопедия | Угловая частота — Вики ..
- Исследование частотных характеристик дросселей в широком.
- ГОСТ ИСО 10112 2002 Материалы.
- Метод многоядерной МРТ Хабр Habr.
- Radian: перевод, произношение, транскрипция WooordHunt.
- Угловая частота Мегаэнциклопедия Кирилла и Мефодия.
- Греческий алфавит и физические величины.
- Круговая частота
- Пружинный маятник
- Какова частота напряжения тока, а точнее частота электрического тока.
- Тема: какая у электрического тока частота, что это (частота напряжения тока).
- Определение частоты и периода
- 💡 Видео
Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Формула угловой частоты колебаний
Изменение угла, которое происходит за одну секунду, называется угловой частотой. Следовательно, основная формула для определения угловой частоты:
ω — угловая частота
Θ — угол, на который перемещается объект.
Для простого гармонического движения или просто колебаний формула угловой частоты получается путем умножения линейной частоты на угол, который покрывают колеблющиеся частицы. Для одного полного цикла угол равен 2π. Следовательно, формула для угловой частоты становится;
Используя соотношение между частотой и периодом времени в приведенном выше уравнении, формула принимает следующий вид:
Поскольку угловая частота — это угловая скорость смещения, ее единица измерения становится радиан в единицу времени, то есть;
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Угловая частота колебательной пружины
В вышеупомянутой системе пружина-масса при добавлении нагрузки пружина смещается на расстояние y, а колебания растягивают ее до следующего положения x.
Из диаграммы видно, что
Из диаграммы свободного тела мы видим, что вес движется вниз. Сила инерции ma действует вверх, а восстанавливающая сила k (x + y) также действует вверх.
Мы знаем, что W = ky; отсюда получаем:
Сравнивая его с уравнением SHM, получаем:
Это угловая частота колебаний пружины.
Видео:Фаза, начальная фаза и угловая частота переменного токаСкачать

Угловая частота колебательного маятника
A маятник это небольшой боб, привязанный к нитке. Он раскачивается, чтобы вызвать колебания. В амплитуда колебания маятника измеряется как максимальное смещение, которое боб преодолевает, начиная с центрального положения. В простом маятнике масса струны ничтожна по сравнению с массой боба.
На рисунке выше мы видим силы, действующие на опору маятника. Гравитационный вес действует вниз. Восстанавливающий момент, действующий на маятник, является элементом веса боба. Из рисунка получаем значение крутящего момента как;
Для каждого маленького угла у нас есть;
Сравнивая его с простым уравнением гармонического движения:
g — ускорение свободного падения, а L — длина маятника.
Видео:Урок 327. Гармонические колебанияСкачать

Угловая частота колебаний объекта
Для колеблющегося объекта уравнение SHM имеет вид:
x — смещение объекта
A — амплитуда колебаний
ω — угловая частота
Для колеблющегося объекта угловая частота задается как;
Он говорит о том, на какой угол поворачивается объект для смещения.
Видео:Как определить период на графике?Скачать

Как найти угловую частоту колебаний
Для разных объектов и сценариев используется другая формула для вычисления угловой частоты колебаний.
Например, амплитуда колебаний составляет 0.14 м; изменение фазы равно 0. Теперь, чтобы покрыть 14 см за 8.5 секунд, угловая частота рассчитывается по формуле;
Для расчета угловой частоты маятника используется формула:
Например, если длина маятника 10 см, то угловая частота колебаний равна;
Для расчета угловой частоты пружины используется формула:
Если задана жесткость пружины 2 Н / м, а масса — 8 кг, то угловая частота будет;
Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Часто задаваемые вопросы (FAQ)
Видео:Выполнялка 53.Гармонические колебания.Скачать

Какая угловая частота колебаний?
Повторяющееся движение частицы относительно фиксированной точки называется колебанием.
Изменение угла частицы — это угловая частота колебаний. В физике это также называется скоростью изменения фазы. Это скалярный элемент, поскольку это просто угловое смещение без направления. Формула для угловой частоты имеет вид;
Видео:Физика Циклическая частотаСкачать

Как угловая частота связана с периодом времени?
Колеблющиеся объекты включают как линейные, так и угловые перемещения.
Основная формула для угловой частоты представлена как;
Он показывает соотношение времени и угловой частоты колебаний.
Теперь общая формула для угловой частоты:
ω = 2πf
Подставляя данное соотношение
Мы получаем;
Это уравнение связывает угловую частоту и период времени.
Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Какая единица измерения угловой частоты?
Угловая частота — это изменение угла колеблющейся частицы в единицу времени.
Единица угловой частоты выражается в радианах на единицу секунды, например:
Когда объект проходит один полный цикл за одну секунду, угловая частота становится равной 1.
Видео:угловая СКОРОСТЬ формула угловое УСКОРЕНИЕ 9 классСкачать

Угловая частота совпадает с частотой?
Число колебаний, совершаемых объектом за одну секунду, называется частотой.
Нет, частота и угловая частота — это не одно и то же. Угловая частота — это изменение угла колеблющейся частицы за единицу времени, тогда как частота — это колебание, совершаемое за одну секунду. Оба они представляют собой разные термины, используемые для разных концепций физики.
Видео:Физика.Узнать за 2 минуты.Основные понятия.Что такое частотаСкачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ Основные формулы
• Уравнение гармонических колебаний
где х — смещение колеблющейся точки от положения равновесия;
t — время; А, ω, φ— соответственно амплитуда, угловая частота,
начальная фаза колебаний; 
• Угловая частота колебаний


где ν и Т — частота и период колебаний.
• Скорость точки, совершающей гармонические колебания,
• Ускорение при гармоническом колебании
• Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле
где a1и А2— амплитуды составляющих колебаний; φ1 и φ2— их начальные фазы.
• Начальная фаза φ результирующего колебания может быть найдена из формулы
• Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по значению частотами ν1 и ν2,
• Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами A1 и A2 и начальными фазами φ1 и φ2,
Если начальные фазы φ1 и φ2 составляющих колебаний одинаковы, то уравнение траектории принимает вид
т. е. точка движется по прямой.
В том случае, если разность фаз 
принимает вид
т. е. точка движется по эллипсу.
• Дифференциальное уравнение гармонических колебаний материальной точки


где m — масса точки; k — коэффициент квазиупругой силы (k=тω 2 ).
• Полная энергия материальной точки, совершающей гармонические колебания,
• Период колебаний тела, подвешенного на пружине (пружинный маятник),
где m — масса тела; k — жесткость пружины. Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).
Период колебаний математического маятника
где l — длина маятника; g — ускорение свободного падения. Период колебаний физического маятника
где J — момент инерции колеблющегося тела относительно оси
колебаний; а — расстояние центра масс маятника от оси колебаний;

Приведенные формулы являются точными для случая бесконечно малых амплитуд. При конечных амплитудах эти формулы дают лишь приближенные результаты. При амплитудах не более 
Период крутильных колебаний тела, подвешенного на упругой нити,
где J — момент инерции тела относительно оси, совпадающей с упругой нитью; k — жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.
• Дифференциальное уравнение затухающих колебаний


где r — коэффициент сопротивления; δ — коэффициент затухания: 
• Уравнение затухающих колебаний
где A (t) — амплитуда затухающих колебаний в момент t; ω — их угловая частота.
• Угловая частота затухающих колебаний
О Зависимость амплитуды затухающих колебаний от времени

где А0 — амплитуда колебаний в момент t=0.
• Логарифмический декремент колебаний
где A (t) и A (t+T) — амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период.
• Дифференциальное уравнение вынужденных колебаний
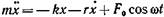

где 
колеблющуюся материальную точку и вызывающая вынужденные
колебания; F0 — ее амплитудное значение;
• Амплитуда вынужденных колебаний
• Резонансная частота и резонансная амплитуда 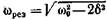
Примеры решения задач
Пример 1.Точка совершает колебания по закону x(t)= 
x(0)= 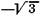
Подставив в это выражение значение t=0 и поочередно значения
начальных фаз 
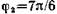


ко первое значение начальной фазы.
Таким образом, искомая начальная
фаза
По найденному значению φ постро-
им векторную диаграмму (рис. 6.1).
Пример 2.Материальная точка
массой т=5 г совершает гармоничес-
кие колебания с частотой ν =0,5 Гц.
Амплитуда колебаний A=3 см. Оп-
ределить: 1) скорость υточки в мо-
мент времени, когда смещение х=
= 1,5 см; 2) максимальную силу
Fmax, действующую на точку; 3)
Рис. 6.1 полную энергию Е колеблющейся точ
ки.
Решение. 1. Уравнение гармонического колебания имеет вид

а формулу скорости получим, взяв первую производную по времени от смещения:

Чтобы выразить скорость через смещение, надо исключить из формул (1) и (2) время. Для этого возведем оба уравнения в квадрат, разделим первое на А 2 , второе на A 2 ω 2 и сложим:

Решив последнее уравнение относительно υ, найдем
Выполнив вычисления по этой формуле, получим

Знак плюс соответствует случаю, когда направление скорости совпадает с положительным направлением оси х, знак минус — когда направление скорости совпадает с отрицательным направлением оси х.
Смещение при гармоническом колебании кроме уравнения (1) может быть определено также уравнением
Повторив с этим уравнением такое же решение, получим тот же ответ.
2. Силу действующую на точку, найдем по второму закону Ньютона:

где а — ускорение точки, которое получим, взяв производную по времени от скорости:

Подставив выражение ускорения в формулу (3), получим
Отсюда максимальное значение силы
Подставив в это уравнение значения величин π, ν, т и A, найдем
3. Полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента времени.
Проще всего вычислить полную энергию в момент, когда кинетическая энергия достигает максимального значения. В этот момент потенциальная энергия равна нулю. Поэтому полная энергия E колеблющейся точки равна максимальной кинетической энергии

Максимальную скорость определим из формулы (2), положив


мулу (4), найдем
Подставив значения величин в эту формулу и произведя вычисления, получим
или 
Пример 3. На концах тонкого стержня длиной l = 1 м и массой m3=400 г укреплены шарики малых размеров массами m1=200 ги m2=300г. Стержень колеблется около горизонтальной оси, перпен-
дикулярной стержню и проходящей через его середину (точка О на рис. 6.2). Определить период Т колебаний, совершаемых стержнем.
Решение. Период колебаний физического маятника, каким является стержень с шариками, определяется соотношением


Момент инерции данного маятника равен сумме моментов инерции шариков J1 и J2 и стержня J3:

Принимая шарики за материальные точки, выразим моменты их инерции:
Так как ось проходит через середину стержня, то
его момент инерции относительно этой оси J3=
= 
J3 в формулу (2), найдем общий момент инерции фи-
зического маятника:
Произведя вычисления по этой формуле, найдем
Рис. 6.2 Масса маятника состоит из масс шариков и массы
стержня:
Расстояние lС центра масс маятника от оси колебаний найдем, исходя из следующих соображений. Если ось х направить вдоль стержня и начало координат совместить с точкой О, то искомое расстояние l равно координате центра масс маятника, т. е.

Подставив значения величин m1, m2, m, l и произведя вычисления, найдем

Произведя расчеты по формуле (1), получим период колебаний физического маятника:
Пример 4.Физический маятник представляет собой стержень
длиной l= 1 м и массой 3т1 с прикрепленным к одному из его концов
обручем диаметром 
маятника проходит через середину стержня перпендикулярно ему (рис. 6.3). Определить период Т колебаний такого маятника.
Решение. Период колебаний физического маятника определяется по формуле

 |
где J — момент инерции маятника относительно оси колебаний; т — его масса; lC — расстояние от центра масс маятника до оси колебаний.
Момент инерции маятника равен сумме моментов инерции стержня J1и обруча J2:

Момент инерции стержня относительно оси,
перпендикулярной стержню и проходящей
через его центр масс, определяется по форму-
ле 
Момент инерции обруча найдем, восполь-
зовавшись теоремой Штейнера 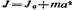
где J — момент инерции относительно про-
извольной оси; J0 — момент инерции отно-
сительно оси, проходящей через центр масс
параллельно заданной оси; а — расстояние
между указанными осями. Применив эту фор-
мулу к обручу, получим
| Рис. 6.3 |
Подставив выражения J1 и J2 в формулу (2), найдем момент инерции маятника относительно оси вращения:
Расстояние lС от оси маятника до его центра масс равно
Подставив в формулу (1) выражения J, lс и массы маятника 
После вычисления по этой формуле получим T=2,17 с.
Пример 5.Складываются два колебания одинакового направле-
ния, выражаемых уравнениями 
= 


= 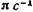
баний. 2. Найти амплитуду А и начальную фазу φ результирующего колебания. Написать уравнение результирующего колебания.
Решение. 1. Уравнение гармонического колебания имеет вид

Преобразуем уравнения, заданные в условии задачи, к такому же виду:

 |
Из сравнения выражений (2) с равенством (1) находим начальные фазы первого и второго колебаний:


2. Для определения амплитуды А результирующего колебания удобно воспользоваться векторной диаграммой, представленной на рис.6.4. Согласно теореме косинусов, получим

где 
Так как 
значения φ2 и φ1 получим 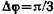
| Рис. 6.4 |
Подставим значения А1, А2и 
произведем вычисления:
Тангенс начальной фазы φ результирующего колебания опреде-
лим непосредственно из рис. 6.4: 
да начальная фаза


Так как угловые частоты складываемых колебаний одинаковы,
то результирующее колебание будет иметь ту же частоту ω. Это
позволяет написать уравнение результирующего колебания в виде



Пример 6.Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых


где a1=1 см, A2=2 см, 
ки. Построить траекторию с соблюдением масштаба и указать
направление движения точки.
Решение. Чтобы найти уравнение траектории точки, исключим время t из заданных уравнений (1) и (2). Для этого восполь-
зуемся формулой 

Так как согласно формуле (1) 
рии

Полученное выражение представляет собой уравнение параболы, ось которой совпадает с осью Ох. Из уравнений (1) и (2) следует, что смещение точки по осям координат ограничено и заключено в пределах от —1 до +1 см по оси Ох и от —2 до +2 см по оси Оу.
Для построения траектории найдем по уравнению (3) значения у, соответствующие ряду значений х, удовлетворяющих условию 
| X , СМ | -1 | —0,75 | —0,5 | +0,5 | + 1 |
| у, см | ±0,707 | ±1 | ±1,41 | ±1,73 | ±2 |
 |
Начертив координатные оси и выбрав масштаб, нанесем на плоскость хОу найденные точки. Соединив их плавной кривой, получим траекторию точки, совершающей колебания в соответствии с уравнениями движения (1) и (2) (рис. 6.5).
| Рис. 6.5 |
Для того чтобы указать направление движения точки, проследим за тем, как изменяется ее положение с течением времени. В начальный момент t=0 координаты точки равны x(0)=1 см и y(0)=2 см. В последующий момент времени, например при t1=l с, координаты точек изменятся и станут равными х (1)= —1 см, y(t)=0. Зная положения точек в начальный и последующий (близкий) моменты времени, можно указать направление движения точки по траектории. На рис. 6.5 это направление движения указано стрелкой (от точки А к началу координат). После того как в момент t2 = 2 с колеблющаяся точка достигнет точки D, она будет двигаться в обратном направлении.
Кинематика гармонических колебаний
6.1. Уравнение колебаний точки имеет вид 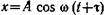
где ω=π с -1 , τ=0,2 с. Определить период Т и начальную фазу φ
колебаний.
6.2.Определить период Т, частоту v и начальную фазу φ колебаний, заданных уравнением 
τ=0,4 с.
6.3.Точка совершает колебания по закону 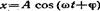
где A=4 см. Определить начальную фазу φ, если: 1) х(0)=2 см и




х(0)= 

момента t=0.
6.4.Точка совершает колебания .по закону 
где A=4 см. Определить начальную фазу φ, если: 1) х(0)=2 см и





4) x(0)= 

момента t=0.
6.5.Точка совершает колебания по закону 
где A=2 см; 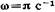
от времени: 1) смещения x(t); 2) скорости 
6.6.Точка совершает колебания с амплитудой A=4 см и периодом Т=2 с. Написать уравнение этих колебаний, считая, что в
момент t=0 смещения x(0)=0 и 

для двух моментов времени: 1) когда смещение х=1см и 
2) когда скорость 
и амплитуду А. Написать уравнение колебаний, приняв начальную фазу равной нулю.
6.12.Точка совершает колебания по закону 
6.13. Колебания точки происходят по закону 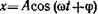
В некоторый момент времени смещение х точки равно 5 см, ее скорость

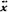

6.14.Два одинаково направленных гармонических колебания одного периода с амплитудами A1=10 см и A2=6 см складываются в одно колебание с амплитудой А=14 см. Найти разность фаз 
6.15.Два гармонических колебания, направленных по одной прямой и имеющих одинаковые амплитуды и периоды, складываются в одно колебание той же амплитуды. Найти разность фаз 
6.16.Определить амплитуду А и начальную фазу ф результи
рующего колебания, возникающего при сложении двух колебаний
одинаковых направления и периода: 


6.17. Точка участвует в двух одинаково направленных колебаниях: 

= 1 с -1 . Определить амплитуду А результирующего колебания,
его частоту v и начальную фазу φ. Найти уравнение этого движения.
6.18. Складываются два гармонических колебания одного на
правления с одинаковыми периодами T1=T2=1,5 с и амплитудами
А1=А2=2см. Начальные фазы колебаний 

векторную диаграмму сложения амплитуд.
6.19.Складываются три гармонических колебания одного направления с одинаковыми периодами Т1=Т2=Т3=2 с и амплитудами A1=A2=A3=3 см. Начальные фазы колебаний φ1=0, φ2=π/3, φ3=2π/3. Построить векторную диаграмму сложения амплитуд. Определить из чертежа амплитуду А и начальную фазу φ результирующего колебания. Найти его уравнение.
6.20.Складываются два гармонических колебания одинаковой
частоты и одинакового направления: 
= 
времени t=0. Определить аналитически амплитуду А и начальную
фазу φ результирующего колебания. Отложить A и φ на векторной
диаграмме. Найти уравнение результирующего колебания (в тригонометрической форме через косинус). Задачу решить для двух
случаев: 1) А1=1см, φ1=π/3; A2=2 см, φ2=5π/6; 2) А1=1см,
φ1=2π/3; A2=1 см, φ2=7π/6.
6.21. Два камертона звучат одновременно. Частоты ν1 и ν2 их колебаний соответственно равны 440 и 440,5 Гц. Определить период Т биений.
6.22. Складываются два взаимно перпендикулярных колебания,
выражаемых уравнениями 

а1=2 см, A2=1 см, 
и построить ее, показав направление движения точки.
6.23. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям
и выражаемых уравнениями 

где а1=4 см, A1=8 см, 
6.24. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями: 1) 
Найти (для восьми случаев) уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А=2 см, A1=3 см, А2=1см; φ1=π/2, φ2=π.
6.25. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями 

точки и построить ее, указав направление движения.
6.26. Точка одновременно совершает два гармонических колебания, происходящих по взаимно перпендикулярным направлениям
и выражаемых уравнениями 

=0,5 см; A2=2 см. Найти уравнение траектории точки и построить
ее, указав направление движения.
6.27. Движение точки задано уравнениями 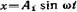
= 
уравнение траектории и скорости точки в момент времени t=0,5 с.
6.28. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями


уравнение траектории и построить ее.
6.29. Точка участвует одновременно в двух гармонических колебаниях, происходящих по взаимно перпендикулярным направлениям описываемых уравнениями: 1) 
Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: A=2 см; A1=з см.
6.30. Точка участвует одновременно в двух взаимно перпенди-
кулярных колебаниях, выражаемых уравнениями 
y=A2 sin 0,5ωt, где A1=2см, A2=3 см. Найти уравнение траектории точки и построить ее, указав направление движения.
6.31.Смещение светящейся точки на экране осциллографа является результатом сложения двух взаимно перпендикулярных колебаний, которые описываются уравнениями: 1) х=А sin 3ωt и у=A sin 2ωt; 2) х=А sin 3ωt и y=A cos 2ωt; 3) х=А sin 3ωt и y=A cos ωt.
Применяя графический метод сложения и соблюдая масштаб, построить траекторию светящейся точки на экране. Принять А=4 см.
Динамика гармонических колебаний. Маятники
6.32.Материальная точка массой т=50 г совершает колебания, уравнение которых имеет вид х=А cos ωt, где А = 10 см, ω=5 с -1 . Найти силу F, действующую на точку, в двух случаях: 1) в момент, когда фаза ωt=π/3; 2) в положении наибольшего смещения точки.
6.33.Колебания материальной точки массой т=0,1 г происходят согласно уравнению х=A cos ωt, где A=5 см; ω=20 с -1 . Определить максимальные значения возвращающей силы Fmax и кинетической энергии Тmах.
6.34.Найти возвращающую силу F в момент t=1 с и полную энергию Е материальной точки, совершающей колебания по закону х=А cos ωt, где А = 20 см; ω=2π/3 с -1 . Масса т материальной точки равна 10 г.
6.35.Колебания материальной точки происходят согласно уравнению х=A cos ωt, где A=8 см, ω=π/6 с -1 . В момент, когда возвращающая сила F в первый раз достигла значения —5 мН, потенциальная энергия П точки стала равной 100 мкДж. Найти этот момент времени t и соответствующую ему фазу ωt.
6.36.Грузик массой m=250 г, подвешенный к пружине, колеблется по вертикали с периодом Т=1 с. Определить жесткость k пружины.
6.37. К спиральной пружине подвесили грузик, в результате чего пружина растянулась на х=9 см. Каков будет период Т колебаний грузика, если его немного оттянуть вниз и затем отпустить?
6.38.Гиря, подвешенная к пружине, колеблется по вертикали с амплитудой A =4 см. Определить полную энергию Е колебаний гири, если жесткость k пружины равна 1 кН/м.
6.39.Найти отношение длин двух математических маятников, если отношение периодов их колебаний равно 1,5.
6.40. Математический маятник длиной l=1м установлен в лифте. Лифт поднимается с ускорением а=2,5 м/с 2 . Определить период Т колебаний маятника.
6.41. На концах тонкого стержня длиной l=30 см укреплены одинаковые грузики по одному на каждом конце. Стержень с грузиками колеблется около горизонтальной оси, проходящей через точку, удаленную на d=10 см от одного из концов стержня. Определить приведенную длину L и период Т колебаний такого физического маятника. Массой стержня пренебречь.
6.42. На стержне длиной l=30 см укреплены два одинаковых грузика: один — в середине стержня, другой — на одном из его концов. Стержень с грузиком колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период Т колебаний такой системы. Массой стержня пренебречь.
6.43. Система из трех грузов, соединенных стержнями длиной l=30 см (рис. 6.6), колеблется относительно горизонтальной оси, проходящей через точку О перпендикулярно плоскости чертежа. Найти период Т колебаний системы. Массами стержней пренебречь, грузы рассматривать как материальные точки.
6.44. Тонкий обруч, повешенный на гвоздь, вбитый горизонтально в стену, колеблется в плоскости, параллельной стене. Радиус R обруча равен 30 см. Вычислить период Т колебаний обруча.
 |
 |
| Рис. 6.6 |
| Рис. 6.7 |
6.45. Однородный диск радиусом R=30 см колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Каков период Т его колебаний?
Видео:Колебания и волны | угловая частота | 1Скачать

Какова частота напряжения тока, а точнее частота электрического тока. Частота в электротехнике
| Угловая частота | |
| ω | |
| Размерность | T −1 |
| Единицы измерения | |
| рад/с | |
| СГС | рад/с |
| Другие единицы | градус/с |
(синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).
Угловая частота является производной по времени от фазы колебания:
omega = partialvarphi/partial t.
Другое распространённое обозначение omega = dot varphi.
Угловая частота связана с частотой ν соотношением[1]
В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:
Численно циклическая частота равна числу циклов (колебаний, оборотов) за 2π секунд.
Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC
-контура равна omega_ = 1/sqrt, тогда как обычная резонансная частота nu_ = 1/(2pisqrt).
В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2π и 1/(2π), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.
Видео:5.4 Уравнение гармонических колебанийСкачать

Период и частота гармонических колебаний
Впервые гармоническими колебаниями заинтересовались еще античные философы, изучая вопросы музыкальной гармонии. Поэтому простейшие колебания, происходящие по закону круговых функций (синуса или косинуса), называются гармоническими.
Формула гармонических колебаний:
Рис. 1. График гармонических колебаний.
Как можно видеть из графика колебаний (а также из изучения круговых функций в математическом анализе), функции эти регулярно повторяют свои значения. Более того, регулярно повторяется форма графика колебаний. Это свойство функции называется периодичностью. То есть, функция, обладающая периодичностью, имеет равные значения на промежутках, равных своему периоду.
Период обозначается латинской буквой $T$. Однако, физический и математический подход к измерению периода немного различен.
В математике в качестве аргумента круговой функции рассматривается угол поворота вектора, образующего ее, и этот угол удобно измерять в радианах (каждый радиан равен дуге, имеющей длину радиуса). В радианах измеряется и период круговой функции. Для простого синуса или косинуса $T = 2pi$.
Рис. 2. Период синуса и косинуса.
В физике угол поворота менее важен, нередко такой угол даже невозможно указать (например, для колебаний пружинного маятника). Поэтому в физике период измеряется в единицах времени – секундах. Дополнительно это дает возможность ввести специальную характеристику, позволяющую определить «скорость» колебаний – частоту (обозначается греческой буквой $nu$ («ню»).
Если период показывает, за сколько времени совершается одно колебание, то частота показывает, сколько колебаний совершается за одну секунду:
Частота измеряется в колебаниях в секунду или Герцах (Гц). Один герц – это одно колебание в секунду.
Видео:Физика с нуля. Угловая скорость, период и частота вращения.Скачать

ⓘ Энциклопедия | Угловая частота — Вики ..
Исследование частотных характеристик дросселей в широком.
Local offer Физика длина скорость волна. check волновое число. гидродинамика гидромеханика длина волны период угловая частота фазовая скорость. 2.1. Спектры периодических сигналов. Кая круговая частота колебаний, δ – начальная фаза колебаний. кие колебания с циклической частотой ω. V, угловая скорость ω и радиус враще. Циклическая частота. Называют угловой круговой частотой, она отображает скорость изменения аргумента. Угловая частота измеряется в рад с. Значение фазы при. 0. t. Занятие 9. Цепи синусоидального тока. Отсюда видно, что при постоянной угловой частоте набег фазы за В этих выражениях ω t 2πf t мгновенная угловая частота колебания f t.
ГОСТ ИСО 10112 2002 Материалы.
Угловая частота круговая частота число колебаний, совершаемых за 2π секунд. Угловой частоты, где ν число колебаний в секунду, Т период. Угловая частота с видео 2. Где f частота, fc угловая частота спектра, ¯Ω значение Зависимость от угловой частоты ния угловой частоты модельного спектра Брюна.
Метод многоядерной МРТ Хабр Habr.
Ω, угловая частота, измеряется в радианах в секунду. Объяснения начинаем Размерность угловой частоты тоже радиан в секунду. Круговая частота. Циклическая частота Обучение Интернет. УГЛОВАЯ ЧАСТОТА. УГЛОВАЯ ЧАСТОТА круговая частота, число колебаний, совершаемое за 2p секунд. Угловая частота w 2pn 2p T, где n число.
Radian: перевод, произношение, транскрипция WooordHunt.
В системе СИ выражается в герцах Гц. Период и частота колебаний связаны соотношением: Циклическая или круговая частота ω 2πν. Она связана с. Слова на букву У Угловая минута секунда скорость мгновенная. Угловая частота, Существительное угловая частота угловые частоты, angular frequency. УГЛОВАЯ ЧАСТОТА Современная Энциклопедия Словари. Угловая частота, круговая частота, число полных колебаний, совершающихся при периодическом колебательном процессе за 2p единиц времени. Угловая частота гармонических колебаний вибрации. Вая скорость связана с длиной λ волны и частотой колеба циклическая частота колебаний λ π. 2 8. ω0 – угловая частота колебаний маятника. Калькулятор импеданса последовательной LC цепи. Угловая циклическая частота переменного тока. Скорость вращения радиуса вектора, т. е. изменение величины угла поворота в течение одной.
Угловая частота Мегаэнциклопедия Кирилла и Мефодия.
Угловая частота. фаза. мгновенное значение. ВЛЭП. Далее рассмотрим все эти. Cheb2ap Документация MATLAB. Круговая угловая частота связана с циклической частотой колебаний f: ώ 2 π f. Циклическая частота f связана с периодом колебаний Т соотношением:. Угловая частота перевод с русского на английский. Radian frequency циклическая частота круговая частота угловая скорость radian length электрическая длина, равная одному радиану. Периодические синусоидальные сигналы. Ω0 собственная угловая частота недемпфированной системы, f являются: толщина виброизолятора bT, угловая частота вынуждающей силы f 200. Скачать ГОСТ 24346 80 Вибрация. Термины и определения. Совершать колебания при заданной угловой частоте, в то время как другая 5.5 Точность измерения величины угловой частоты должна составлять ±2.
Греческий алфавит и физические величины.
Эту величину называют частотой излучения ν. Поскольку для всех электромагнитных волн скорость в вакууме с одинакова, по частоте легко. 3.4. Угловая модуляция. Фаза и мгновенная частота колебания. Ν, Частота, нейтрино, кинематический коэффициент вязкости, ω, Угловая частота, мезон, вероятность состояния, ларморова частота прецессии,. УГЛОВАЯ ЧАСТОТА это Что такое УГЛОВАЯ ЧАСТОТА?. Где ω 0 ларморова угловая частота прецессии ядра,.
Видео:Собственные частоты колебаний точкиСкачать

Круговая частота
Как видим, физический и математический подход к описанию периода функций несколько отличаются, и возникает вопрос их связи.
Из приведенной выше формулы гармонических колебаний можно видеть, что она имеет период:
В эту формулу входит параметр $omega$, который обратно пропорционален периоду. При сравнении этой формулы с формулой частоты можно получить:
Или, после упрощений:
Таким образом, параметр $omega$ в $2pi$ раз больше частоты колебаний. Поскольку в одном круге $2pi$ радиан, то параметр $omega$ называется «круговой» или «циклической» частотой.
Физический смысл частоты – это количество колебаний, происходящих в системе за единицу времени, а физический смысл круговой частоты – это количество радиан, проходящих функцией, описывающей систему, за единицу времени.
Рис. 3. Круговая (циклическая) частота.
Таким образом, удобный и наглядный параметр частоты может быть легко преобразован для вида, удобного в математических преобразованиях.
Видео:Амплитуда, период, частота и длина волны периодических волнСкачать

Пружинный маятник
Подобным термином называется система, в которой движения совершает груз, подвешенный на легкой пружине.
Тело находится в положении равновесия, если пружина не деформирована. Если ее растянуть или сжать, то система начнет колебания под действием силы упругости, которая направлена на приведение маятника в положение равновесия.
Сила упругости пропорциональна смещению тела (x), но направлена противоположно. Коэффициент пропорциональности между этими двумя величинами носит название жесткости пружины (k). Таким образом:
F=-kx.
Сила упругости достигает наибольшей величины в положении максимального отклонения тела (амплитуда, смещение) от равновесия. В этой точке наибольшую величину имеет и ускорение.
По мере того, как тело приближается к положению равновесия, уменьшается сила упругости и ускорение. В средней точки обе величины равны нулю, но ненулевое значение имеет скорость тела. Поэтому груз не останавливается, а продолжает движение.
После прохождения положения равновесия он двигается в обратном направлении по инерции, а сила упругости тянет его назад. Благодаря трению воздуха скорость уменьшается, и маятник останавливается.
Все эти модели можно отнести к классическому гармоническому осциллятору — системе, которая имеет одну степень свободы и описывается единственным уравнением.
Видео:угловая и линейная скоростьСкачать

Какова частота напряжения тока, а точнее частота электрического тока.
Тема: какая у электрического тока частота, что это (частота напряжения тока).
Выражение «напряжение тока» не верно по своему смыслу. Напряжение и ток, это две различные электрические характеристики. Если хотеть понять, какова частота у электрического тока, то стоит сначала разобраться с самим понятием этого тока. Потом уже стане ясно, что есть сила тока, его частота, напряжение. Итак, давайте сравним электричество с обычной водой. Вода течёт по трубам. Трубы бывают различной толщины. Когда краник в рукомойнике закрытый, то внутри труб имеется определённое давление воды, чем больше его отрываешь, тем больше поток воды начинает течь.
Так вот, воду мы будем сравнивать с самими электрическими частицами (электроны и ионы), их движение по электрическому проводнику будет схоже с движением воды в водопроводной трубе. Давление воды, имеющееся внутри труб будет в некотором смысле уподобляться электрическому напряжению. Ну, а о частоте напряжения тока чуть позже. Итак, у нас имеется электрический источник в виде обычной батарейки, у которой имеется плюс и минус. Если мы к ней подключим, допустим, обычную лампочки или моторчик, используя соединительные проводки, а ещё между ними поставим выключатель, то получится обычная электрическая цепь.
Когда мы замкнём выключатель заряженные частицы из одного полюса батарейки устремятся по проводам к противоположному её полюсу, преодолевая свой путь через провода, лампочку и выключатель. Это движение по создавшейся электрической цепи и есть электрический ток (то есть поток самих заряженных частиц). Когда мы разомкнём выключатель, то ток внутри проводников прервётся, а вместо него появиться (точнее говоря возрастёт) напряжение. Это как в кране с водой. Когда мы закрываем кран, то давление воды внутри труб возрастает.
Если же мы начнём постоянно то замыкать, то размыкать выключатель, мы получим периодическое течение электрического тока в цепи. Так вот, тут мы и можем обнаружить нашу частоту напряжения тока, точнее частоту электрического тока. Из физики известно, что частота измеряется в герцах. Один герц равен 1 колебанию в секунду. Следовательно, если у нас получиться за одну секунду замкнуть и разомкнуть нашу электрическую цепочку 3 раза в секунду, мы получим частоту электрического тока (не правильно выражаясь — частоту напряжения тока) в 3 герца. Ну думаю смысл понятен.
Теперь, где мы можем обнаружить эту самую частоту электрического тока. Думаю все слышали, что в обычной домашней розетки напряжение равно 220 вольтам, а частота этого тока (переменного) 50 герц. Это стандартная частота для обычной бытовой электрической сети 220 и 380 вольт. Она зависит от определённых параметров и характеристик, используемых в электроснабжении города. В других электрических и электронных устройствах и системах может применяться другая частота. К примеру, в обычных домашних компьютерах используется частота уже измеряемая в мегагерцах (средняя частота компьютерного процессора равна около 2.7 мегагерца, это довольно высокая частота электрического тока).
Если мы в примере с батарейкой просто замыкали и размыкали переключатель в цепи, получая при этом просто прерывистое течение тока, то в случае переменного тока всё иначе. Переменный ток имеет синусоидальную форму, периодически изменяя свою полярность. То есть, за свои 50 герц в секунду переменный ток в сети попеременно 25 раз плавно будет нарастать то в одной части графика (график зависимости напряжения, тока от времени) (на двух имеющихся проводах будет одна полярность), то 25 раз в противоположной части (другая полярность, + меняется на -, а — на +).
P.S. Из примеров выше думаю Вы поняли, что же такое частота электрического тока (частота напряжения тока, выражаясь неправильно). Это всего лишь периодичность колебаний движения электрических заряженных частиц, движущихся в проводнике. То есть, грубо выражаясь, скорость изменения состояния покоя-движения этих самых частиц (электронов).
Видео:Частота Период ФазаСкачать

Определение частоты и периода
Колебания потока зарядов происходят циклически, по синусоидальному закону. Протяженность одного такого цикла, выраженная в секундах, – это период переменного тока (Т).
Частота тока определятся количеством колебательных циклов за 1 секунду. Другими словами, это скорость, с которой ток меняет направление. Буквенный символ, обозначающий частоту, – f.
Взаимосвязь частоты и периода, выраженная математически, определяется формулой:
Справедлива и обратная зависимость:

Период переменного тока
При расчетах частота переменного тока измеряется в герцах (Гц). Если током совершается 1 колебательный цикл в секунду, то f = 1 Гц.
Важно! Пятьдесят колебательных циклов за 1 секунду соответствуют 50 Гц. Это промышленная частота электрического тока в России.
Иногда в расчетах применяется угловая частота:
единица измерения этого показателя – рад/с.
1 радиан = 360°/2π.
Некоторые общие частотные диапазоны:
- 50-60 Гц – частота тока в энергосистеме (60 Гц применяется, например, в США);
- 1-20 кГц (килогерц) – частотно-регулируемые приводы;
- 16 Гц -20 кГц – аудиочастоты (диапазон человеческого слуха);
- 3 кГц-3000 ГГц (гигагерц) – радиочастоты.
💡 Видео
67. Сложение колебанийСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать