При практическом построении прямой по ее уравнению наиболее точный график получится тогда, когда координаты взятых для ее построения двух точек — целые числа.
1. Если прямая определена общим уравнением Ax + By + C = 0 и 
, то для ее построения проще всего определить точки пересечения прямой с координатными осями.
Укажем, как определить координаты точек пересечения прямой с координатными осями. Координаты точки пересечения прямой с осью Ox находят из следующих соображений: ординаты всех точек, расположенных на оси Ox, равны нулю. В уравнении прямой полагают, что y равно нулю, и из полученного уравнения находят x. Найденное значение x и есть абсцисса точки пересечения прямой с осью Ox. Если окажется, что x = a, то координаты точки пересечения прямой с осью Ox будут (a, 0).
Чтобы определить координаты точки пересечения прямой с осью Oy, рассуждают так: абсциссы всех точек, расположенных на оси Oy, равны нулю. Взяв в уравнении прямой x равным нулю, из полученного уравнения определяют y. Найденное значение y и будет ординатой пересечения прямой с осью Oy. Если окажется, например, что y = b, то точка пересечения прямой с осью Oy имеет координаты (0, b).
Пример. Прямая 2x + y — 6 = 0 пересекает ось Ox в точке (3, 0). Действительно, взяв в этом уравнении y = 0, получим для определения x уравнение 2x — 6 = 0, откуда x = 3.
Чтобы определить точку пересечения этой прямой с осью Oy, положим в уравнении прямой x = 0. Получим уравнение y — 6 = 0, из которого следует, что y = 6. Таким образом, прямая пересекает координатные оси в точках (3, 0) и (0, 6).
Если же в общем уравнении прямой C = 0, то прямая, определяемая этим уравнением, проходит через начало координат. Таким образом, уже известна одна ее точка, и для построения прямой остается только найти еще одну ее точку. Абсциссу x этой точки задают произвольно, а ординату y находят из уравнения прямой.
- Точка пересечения прямых в пространстве онлайн
- Предупреждение
- Точка пересечения прямых в пространстве − теория, примеры и решения
- 1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
- 2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
- 3. Точка пересечения прямых в пространстве, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
- Пересечение с осями онлайн
- Другие полезные разделы:
- Оставить свой комментарий:
- 💥 Видео
Видео:Нахождение координат точек пересечения графика функции с осями координатСкачать
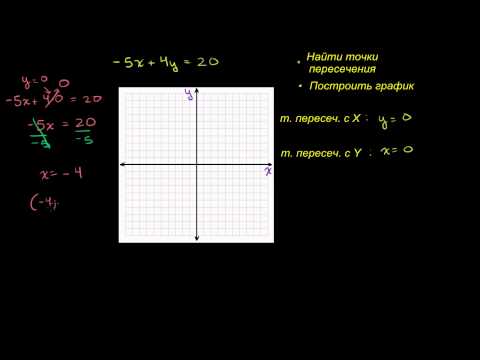
Точка пересечения прямых в пространстве онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Точки пересечения прямой с осями координат X и YСкачать
Точка пересечения прямых в пространстве − теория, примеры и решения
- Содержание
- 1. Точка пересечения прямых, заданных в каноническом виде.
- 2. Точка пересечения прямых, заданных в параметрическом виде.
- 3. Точка пересечения прямых, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
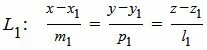 , | (1) |
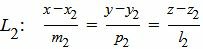 , | (2) |
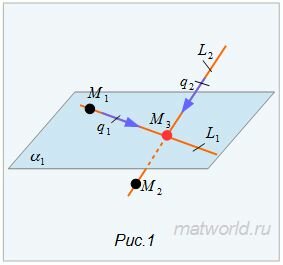
Найти точку пересечения прямых L1 и L2 (Рис.1).
 |
Запишем уравнение (1) в виде системы двух линейных уравнений:
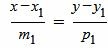 , | (3) |
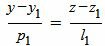 | (4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
| p1(x−x1)=m1(y−y1) |
| l1(y−y1)=p1(z−z1) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p1x−m1y=p1x1−m1y1, | (5) |
| l1y−p1z=l1y1−p1z1. | (6) |
Аналогичным образом преобразуем уравнение (2):
Запишем уравнение (2) в виде системы двух линейных уравнений:
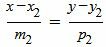 , | (7) |
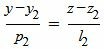 | (8) |
Сделаем перекрестное умножение в уравнениях (7) и (8):
| p2(x−x2)=m2(y−y2) |
| l2(y−y2)=p2(z−z2) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p2x−m2y=p2x2−m2y2, | (9) |
| l2y−p2z=l2y2−p2z2. | (10) |
Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:
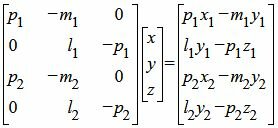 | (11) |
Как решить систему линейных уравнений (11)(или (5), (6), (9), (10)) посмотрите на странице Метод Гаусса онлайн. Если система линейных уравнениий (11) несовместна, то прямые L1 и L2 не пересекаются. Если система (11) имеет множество решений, то прямые L1 и L2 совпадают. Единственное решение системы линейных уравнений (11) указывает на то, что это решение определяет координаты точки пересечения прямых L1 и L2 .
2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
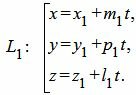 | (12) |
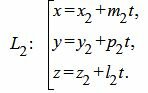 | (13) |
Задачу нахождения нахождения точки пересечения прямых L1 и L2 можно решить разными методами.
Метод 1. Приведем уравнения прямых L1 и L2 к каноническому виду.
Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:
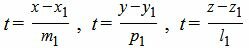 | (14) |
Так как левые части уравнений (14) равны, то можем записать:
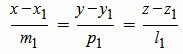 | (15) |
Аналогичным образом приведем уравнение прямой L2 к каноническому виду:
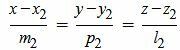 | (16) |
Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямых L1 и L2 решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:
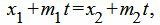 | (17) |
 | (18) |
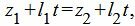 | (19) |
Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).
3. Точка пересечения прямых в пространстве, заданных в разных видах.
Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.
4. Примеры нахождения точки пересечения прямых в пространстве.
Пример 1. Найти точку пересечения прямых L1 и L2:
 | (20) |
 | (21) |
Представим уравнение (20) в виде двух уравнений:
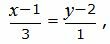 | (22) |
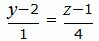 | (23) |
Сделаем перекрестное умножение в уравнениях (22) и (23):
 |
 |
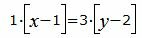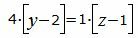Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
 |
 |
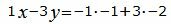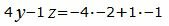Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
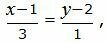 | (26) |
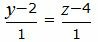 | (27) |
Сделаем перекрестное умножение в уравнениях (7) и (8)
 |
 |
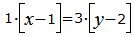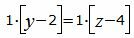Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
 |
 |
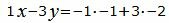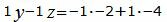Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
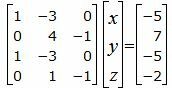 | (30) |
Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 |
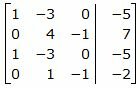Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1:
 |
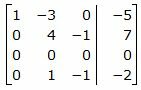Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:
 |
Сделаем перестановку строк 3 и 4.
 |
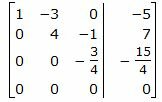Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:
 |
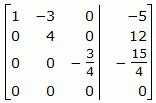Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:
 |
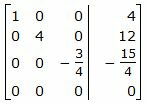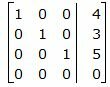
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 |
 |
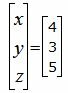Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
 | (31) |
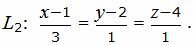 | (32) |
Приведем параметрическое уравнение прямой L1 к каноническому виду. Выразим параметр t через остальные переменные:
 |
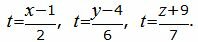Из равентсв выше получим каноническое уравнение прямой:
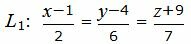 | (33) |
Представим уравнение (33) в виде двух уравнений:
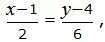 | (34) |
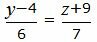 | (35) |
Сделаем перекрестное умножение в уравнениях (34 и (35):
 |
 |
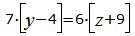Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
 |
 |
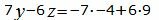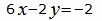 | (36) |
 . | (37) |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
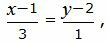 | (38) |
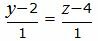 | (39) |
Сделаем перекрестное умножение в уравнениях (38) и (39)
 |
 |
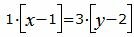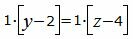Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
 |
 |
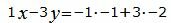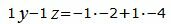Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
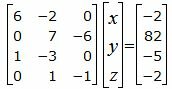 | (42) |
Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:
 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:
 |
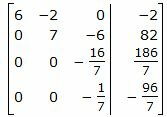Исключим элементы 3-го столбца матрицы ниже элементаa33. Для этого сложим строку 4 со строкой 3, умноженной на -1/16:
 |
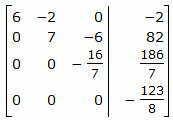Из расширенной матрицы восстановим последнюю систему линейных уравнений:
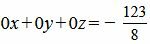 | (43) |
Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L1 и L2 не пересекаются. То есть они или параллельны, или скрещиваются.
Прямая L1 имеет направляющий вектор q1=, а прямая L2 имеет направляющий вектор q2=. Эти векторы не коллинеарны. Следовательно прямые L1 и L2 скрещиваются .
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать
Пересечение с осями онлайн
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, предназначен для решения задачи нахождения точек пересечения графика функции с осями координат.
Найти точки пересечения функции с осями координат:
При проведении исследования функции, возникает задача нахождения точек пересечения этой функции с осями координат. Рассмотрим на конкретном примере алгоритм решения такой задачи. Для простоты будем работать с функцией одной переменной:
График данной функции представлен на рисунке:
Как следует из рисунка, наша функция пересекает ось в двух точках, а ось — в одной.
Сначала найдём точки пересечения функции с осью . Сразу отметим, что в этих точках координата . Поэтому для их поиска, нам нужно решить уравнение:
Таким образом, мы нашли две точки пересечения нашей функции с осью абсцисс: и . Стоит отметить, что задача поиска пересечений функции с осью эквивалентна задаче нахождения нулей функции.
Теперь найдём точку пересечения с осью ординат. В этой точке координата . Поэтому для их поиска, просто подставляем значение в нашу функцию:
Таким образом, мы нашли точку пересечения нашей функции с осью ординат .
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать
Другие полезные разделы:
Видео:8 класс. Найти координаты точек пересечения параболы с осями координатСкачать
Оставить свой комментарий:
Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме
💥 Видео
Как найти точки пересечения прямой с осями координатСкачать
Исследование функции. Часть 3. Точки пересечения с осями координатСкачать
№975. Найдите координаты точек пересечения прямой 3x-4y + 12 = 0 с осями координатСкачать
Точки пересечения графика линейной функции с координатными осями. Практическая часть. 7 класс.Скачать
Не выполняя построения графиков, найдите координаты точки пересечения прямых. Алгебра 7 класс.Скачать
№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Составляем уравнение прямой по точкамСкачать
Точки пересечения прямой с осями координат X и YСкачать
17.2 Вычислите координаты точек пересечения графиков функции с осями координатСкачать
Точки пересечения прямой с осями координат X и Y. Часть 2Скачать
Точки пересечения прямой с осями Х и YСкачать
Точки пересечения с осями координат. Нули функции.Скачать
Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать
УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать
