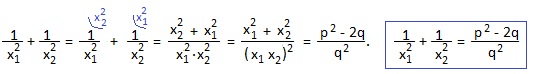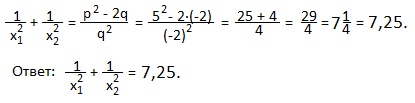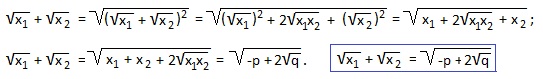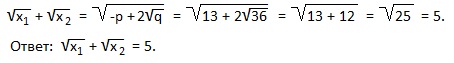Как найти сумму квадратного уравнения

теория по математике 📈 уравнения

Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b 2 –4ac

Если D>0, то уравнение имеет два различных

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Видео:Найти сумму корней квадратного уравнения, если дискриминант равен нулюСкачать

Теорема Виета

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

Данное уравнение является квадратным. Но в его условии присутствует квадратный

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.

Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):

х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0

Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:

х 2 − 2 х − 24 = 0

Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.

Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:Найти значение суммы и произведения корней квадратного уравненияСкачать

8.2.4. Применение теоремы Виета

Часто требуется найти сумму квадратов (x₁ 2 +x₂ 2 ) или сумму кубов (x₁ 3 +x₂ 3 ) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:

Помочь в этом может теорема Виета:

Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Выразим через p и q:

1) сумму квадратов корней уравнения x 2 +px+q=0;

2) сумму кубов корней уравнения x 2 +px+q=0.

Решение.

1) Выражение x₁ 2 +x₂ 2 получится, если взвести в квадрат обе части равенства x₁+x₂=-p;

(x₁+x₂) 2 =(-p) 2 ; раскрываем скобки: x₁ 2 +2x₁x₂+ x₂ 2 =p 2 ; выражаем искомую сумму: x₁ 2 +x₂ 2 =p 2 -2x₁x₂=p 2 -2q. Мы получили полезное равенство: x₁ 2 +x₂ 2 =p 2 -2q.

2) Выражение x₁ 3 +x₂ 3 представим по формуле суммы кубов в виде:

Еще одно полезное равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q).

Примеры.

3) x 2 -3x-4=0. Не решая уравнение, вычислите значение выражения x₁ 2 +x₂ 2 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения

x₁+x₂=-p=3, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 1) равенство:

x₁ 2 +x₂ 2 =p 2 -2q. У нас -p=x₁+x₂=3 → p 2 =3 2 =9; q=x₁x₂=-4. Тогда x₁ 2 +x₂ 2 =9-2·(-4)=9+8=17.

4) x 2 -2x-4=0. Вычислить: x₁ 3 +x₂ 3 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения x₁+x₂=-p=2, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 2) равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q)=2·(2 2 -3·(-4))=2·(4+12)=2·16=32.

Ответ: x₁ 3 +x₂ 3 =32.

Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.

5) 2x 2 -5x-7=0. Не решая, вычислить: x₁ 2 +x₂ 2 .

Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x 2 -2,5x-3,5=0.

По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.

Решаем так же, как пример 3), используя равенство: x₁ 2 +x₂ 2 =p 2 -2q.

x₁ 2 +x₂ 2 =p 2 -2q=2,5 2 -2∙(-3,5)=6,25+7=13,25.

Ответ: x₁ 2 +x₂ 2 =13,25.

6) x 2 -5x-2=0. Найти:

Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x₁ 2 +x₂ 2 =p 2 -2q.

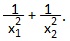
В нашем примере x₁+x₂=-p=5; x₁∙x₂=q=-2. Подставляем эти значения в полученную формулу:

7) x 2 -13x+36=0. Найти:

Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.

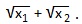
У нас x₁+x₂=-p=13; x₁∙x₂=q=36. Подставляем эти значения в выведенную формулу:

Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Теорема Виета для квадратного уравнения

О чем эта статья:

Видео:Вариант 17, № 2. Теорема Виета. Сумма корней квадратного уравненияСкачать

Основные понятия

Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Существует три вида квадратных уравнений:

• не имеют корней;
• имеют один корень;
• имеют два различных корня.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Формула для его поиска записывается так: D = b 2 − 4ac. Его свойства:

• если D 0, есть два различных корня.

В случае, когда второй коэффициент четный, можно воспользоваться формулой нахождения дискриминанта , где .

В математике теоремой принято называть утверждение, у которого ранее было сформулировано доказательство.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Рассмотрим квадратное уравнение, в котором первый коэффициент равен 1: . Такие уравнения называют приведенными квадратными уравнениями. Сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Обучение на курсах по математике помогает быстрее разобраться в новых темах и подтянуть оценки в школе.

Видео:СУММА КОЭФФИЦИЕНТОВ: Как решать Квадратные Уравнения по МАТЕМАТИКЕ 8 классСкачать

Доказательство теоремы Виета

Дано квадратное уравнение x 2 + bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:

Докажем, что следующие равенства верны

• x₁ + x₂ = −b,
• x₁ * x₂ = c.

Чтобы найти сумму корней x₁ и x₂ подставим вместо них то, что соответствует им из правой части формул корней. Напомним, что в данном квадратном уравнении x 2 + bx + c = 0 старший коэффициент равен единице. Значит после подстановки знаменатель будет равен 2.

Объединим числитель и знаменатель в правой части.

Раскроем скобки и приведем подобные члены:

Сократим дробь полученную дробь на 2, остается −b:

Мы доказали: x₁ + x₂ = −b.

Далее произведем аналогичные действия, чтобы доказать о равенстве x₁ * x₂ свободному члену c.

Подставим вместо x₁ и x₂ соответствующие части из формул корней квадратного уравнения:

Перемножаем числители и знаменатели между собой:

Очевидно, в числителе содержится произведение суммы и разности двух выражений. Поэтому воспользуемся тождеством (a + b) * (a − b) = a 2 − b 2 . Получаем:

Далее произведем трансформации в числителе:

Нам известно, что D = b2 − 4ac. Подставим это выражение вместо D.

Далее раскроем скобки и приведем подобные члены:

Сократим:

Мы доказали: x₁ * x₂ = c.

Значит сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком (x₁ + x₂ = −b), а произведение корней равно свободному члену (x₁ * x₂= c). Теорема доказана.

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Обратная теорема Виета

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Она формулируется так:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями x 2 + bx + c = 0.

Обратные теоремы зачастую сформулированы так, что их утверждением является заключение первой теоремы. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это является утверждением.

Видео:Теорема Виета. 8 класс.Скачать

Докажем теорему, обратную теореме Виета

Корни x₁ и x₂ обозначим как m и n. Тогда утверждение будет звучать следующим образом: если сумма чисел m и n равна второму коэффициенту x 2 + bx + c = 0, взятому с противоположным знаком, а произведение равно свободному члену, то числа m и n являются корнями x 2 + bx + c = 0.

Зафиксируем, что сумма m и n равна −b, а произведение равно c.

Чтобы доказать, что числа m и n являются корнями уравнения, нужно поочередно подставить буквы m и n вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями x 2 + bx + c = 0.

Выразим b из равенства m + n = −b. Это можно сделать, умножив обе части на −1:

Подставим m в уравнение вместо x, выражение −m − n подставим вместо b, а выражение mn — вместо c:

При x = m получается верное равенство. Значит число m является искомым корнем.

1. Аналогично докажем, что число n является корнем уравнения. Подставим вместо x букву n, а вместо c подставим m * n, поскольку c = m * n.

   При x = n получается верное равенство. Значит число n является искомым корнем.

Мы доказали: числа m и n являются корнями уравнения x 2 + bx + c = 0.

Видео:Не решая квадратное уравнение, найдите сумму кубов его корнейСкачать

Примеры

Для закрепления знаний рассмотрим примеры решения уравнений по теореме, обратной теореме Виета.

Дано: x 2 − 6x + 8 = 0.

Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2 − 6x + 8 = 0″ height=»59″ src=»https://lh6.googleusercontent.com/tFokx3SM93Hwlr7ZM9BqX1xiHKv_2dUIB9MoNa8RAwSTmQKXdCcqcFXxTZmxNGw7bOVek-RzRXqBkoCqnYMiqIYVwKhfnHeU-7mA03feEqJTlyKB7e-OsTTKgPaOlddfiaTGszcv» width=»99″>

Имея эти два равенства можно подобрать подходящие корни, которые будут удовлетворять как равенству обоим равенствам системы.

Подбор корней удобнее выполнять с помощью их произведения. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. Значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 являются корнями уравнения x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»57″ src=»https://lh3.googleusercontent.com/rohB7Bvd-elMhTxEUuOhKqLJjqLAvo9VlJxZvOnMeDAHARfKT-SYOWb1WXTTWEN2h0oKbLl6wH7lc0IWL_vH3Si2AJGAGXVn8TPFDT_J1Wu2WeoQ-WP1qgXjCnZ99tWUkK2BOvF2″ width=»64″>

Видео:Теорема Виета. Как найти сумму корней, не решая квадратное уравнениеСкачать

Неприведенное квадратное уравнение

Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым, то есть его первый коэффициент равен единице:

ax 2 + bx + c = 0, где а = 1.

Если квадратное уравнение не является приведенным, но задание связано с применением теоремы, нужно обе части разделить на коэффициент, который располагается перед x 2 .

1. Получилось следующее приведенное уравнение:

Получается, второй коэффициент при x равен, свободный член —. Значит сумма и произведение корней будут иметь вид:

Рассмотрим пример неприведенного уравнения: 4x 2 + 5x + 1 = 0. Разделим обе его части на коэффициент перед x 2 , то есть на 4.

📸 Видео

34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать

Решение биквадратных уравнений. 8 класс.Скачать

ТЕОРЕМА ВИЕТА // Как решать Квадратные Уравнения по АЛГЕБРЕ 8 классСкачать

Не решая квадратное уравнение, найдите сумму частного его корнейСкачать

Найти сумму квадратов корней квадратного уравненияСкачать

ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать

Как найти сумму квадратов, корней уравнения?Скачать

Комплексные корни квадратного уравненияСкачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать