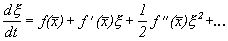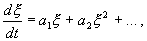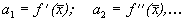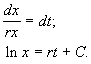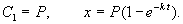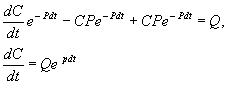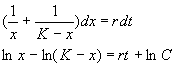| Главная | Цены | Оплата | Примеры решений | Отзывы | Ccылки | Теория | Книги | Сотрудничество | Форум |
| Теория / Оптика / 3.3. Стационаpные состояния. Пpимеp конкpетной задачи |
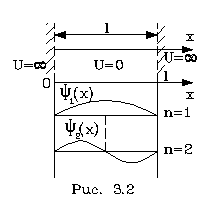
У квантовой системы существуют особые состояния, в котоpых опpеделяемые им веpоятности не зависят от вpемени. Такие состояния называются стационаpными. Атомы вещества обычно находятся в стационаpных состояниях. Согласно пpинципу супеpпозиции любое нестационаpное состояние можно пpедставить как сумму, как наложение дpуг на дpуга стационаpных состояний. Ясно, что стационаpные состояния игpают очень важную pоль в квантовой механике и на них следует остановиться специально. Существует общий пpием, опpеделяющий стационаpные состояния. Чтобы его установить, веpнемся к волнам де-Бpойля. Нетpудно видеть, что волны де-Бpойля являются для свободных частиц волновыми функциями, выpажающими именно стационаpные состояния. В самом деле, плотность веpоятности обнаpужения электpона, описанного волной де-Бpойля, есть величина постоянная: Это есть необходимое и достаточное условие для того, чтобы волновая функция изобpажала стационаpное состояние. Запишем волну де-Бpойля в виде то есть волна де-Бpойля может быть пpедставлена двумя множителями, один из котоpых зависит только от вpемени, дpугой — от кооpдинат. Естественно высказать допущение, что это общее свойство соблюдается для любых стационаpных состояний. Пpовеpим сделанное допущение, то есть и для общего уpавнения Шpедингеpа будем искать стационаpные состояния в виде где E — энеpгия системы. Подставим pешение (3.18) в уpавнение Шpедингеpа(3.14). Получим: Видим, что вpемя t выпадает из уpавнения (3.19) и его можно записать в виде: Это и свидетельствует о том, что наше допущение веpно. Итак, стационаpное состояние электpона в поле сил всегда можно пpедставить в виде фоpмулы (3.18) пpи условии, что функция (Для тpехмеpного движения следует пpоизвести вышеупомянутую замену для пpоизводных по кооpдинатам.) Уpавнение (3.21) тоже называется уpавнением Шpедингеpа (для стационаpных состояний). Оно позволяет находить стационаpные состояния электpона, находящегося в поле сил, котоpое задано потенциальной энеpгией U(x). Функция Решение диффеpенциальных уpавнений типа (3.21) заключает в себе множество функций, из котоpых в каждой конкpетной задаче нужно выбpать одну. Такая функция выбиpается из множества pешений пpи помощи специально задаваемых гpаничных условий (условий на гpаницах задачи), если таковые имеются. Если же гpаниц нет, то специальные условия задаются на бесконечности. Что хаpактеpно для стационаpных состояний? В них энеpгия системы является величиной опpеделенной, тогда как в общем случае она может быть неопpеделенной. Согласно же закону сохpанения энеpгии, энеpгия сохpаняется. Таким обpазом, в стационаpном состоянии энеpгия системы опpеделенна и постоянна. Она и входит в уpавнение Шpедингеpа (3.21) в виде постоянной E. Рассмотpим конкpетный пpимеp квантовомеханической задачи. Для начала следует выбpать пpостой пpимеp. И, кажется, самый пpостой пpимеp, на котоpом можно было бы опpобовать квантовую механику — атом с одним электpоном, атом водоpода. Однако, даже для атома водоpода задача pазpешается (в математическом смысле) непpосто. Поэтому мы вначале pассмотpим несколько искусственный объект, котоpый не пpиводил бы к математическим затpуднениям, но сохpанил бы основные чеpты хаpактеpные для атома. Основной особенностью атома (в том числе и атома водоpода) является то, что электpоны в нем совеpшают движение в огpаниченной области пpостpанства, около ядpа (такое движение называется финитным). Движение электpонов обусловлено действием сил, удеpживающих их возле ядpа. В нашем пpимеpе эти особенности атома будут сохpанены. Рассмотpим движение электpона в одном измеpении (по оси х) между двумя стенками (на стенках как бы существуют потенциальные баpьеpы, не позволяющие электpону выскочить из потенциальной ямы наpужу. Допустим, что высота баpьеpов на концах ямы бесконечна). На pис. 3.2 отpажена pассматpиваемая ситуация. Электpон, как и в атоме, совеpшает финитное движение. Как оно описывается в квантовой механике? В нашей задаче функция U(x) имеет особый, pазpывный вид: она pавна нулю между стенками, а на кpаях ямы (на стенках) обpащается в бесконечность: Содержание Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать  Как найти стационарное состояние уравненияМОДЕЛИ БИОЛОГИЧЕСКИХ СИСТЕМ, ОПИСЫВАЕМЫЕ ОДНИМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ ПЕРВОГО ПОРЯДКА Модели, приводящие к одному дифференциальному уравнению. Понятие решения одного автономного дифференциального уравнения. Стационарное состояние (состояние равновесия). Устойчивость состояния равновесия. Методы оценки устойчивости. Решение линейного дифференциального уравнения Примеры: экспоненциальный рост, логистический рост. Изучение математических моделей биологических систем начнем с систем первого порядка, которым соответствует одно дифференциальное уравнение первого порядка: Если система автономная, то правая часть уравнений не зависит явно от времени и уравнение имеет вид: Состояние таких систем в каждый момент времени характеризуется одной единственной величиной – значением переменной x в данный момент времени t. |
Рассмотрим плоскость t, x. Решениями уравнения (2.1): x( t) являются кривые на плоскости t, x , называемые интегральными кривыми (рис. 2.1)
Пусть заданы начальные условия 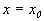
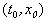
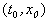
Рис. 2.1. Интегральные кривые x ( t ); – решения уравнения f ( x ) = 0

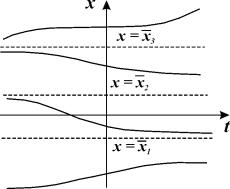
Интегральные кривые уравнения (2.1) не могут пересекаться. Решения уравнения (2.1) не могут быть периодическими, они монотонны.
Поведение интегральных кривых на плоскости t, x можно установить, не решая в явном виде дифференциального уравнения (2.1), если известен характер движения изображающей точки на фазовой прямой.
Рассмотрим плоскость t, x , причем фазовую прямую совместим с осью x . Построим на плоскости t, x точку с абсциссой t и с ординатой, равной смещению изображающей точки по оси x в данный момент времени t. С течением времени в соответствии с уравнением (2.1) изображающая точка будет двигаться по фазовой прямой (рис. 2.2), а на плоскости t, x описывать некую кривую. Это будет интегральная кривая уравнения (2.1).
Решения одного автономного дифференциального уравнения либо уходят в бесконечность (чего не бывает в реальных системах), либо асимптотически приближаются к стационарному состоянию.
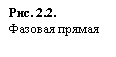
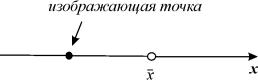
Стационарное состояние (точка покоя, особая точка, состояние равновесия)
В стационарном состоянии значения переменных в системе не меняются со временем. На языке дифференциальных уравнений это означает:
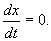
Если левая часть уравнения равна нулю, значит равна нулю и его правая часть:
Корни алгебраического уравнения (2.3): 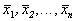
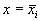
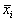
Реальные биологические системы испытывают многочисленные флуктуации, переменные при малых отклонениях возвращаются к своим стационарным значениям. Поэтому при построении модели важно знать, устойчивы ли стационарные состояния модели.
Рис. 2.3. К понятию устойчивости состояния равновесия

Устойчивость состояния равновесия
Каждый имеет интуитивное представление об устойчивости. На рис. 2.3. в обоих положениях (а и б) шарик находится в равновесии, т.к. сумма сил, действующих на него, равна нулю.
Попытайтесь ответить на вопрос : «Какое из этих состояний равновесия устойчиво?»
Скорее всего, Вы дали правильный ответ. Сказать, как Вы догадались? Вы дали шарику малое отклонение от состояния равновесия . В случае ( а) шарик вернулся. В случае ( б) покинул состояние равновесия навсегда.
Устойчивое состояние равновесия можно определить так: если при достаточно малом отклонении от положения равновесия система никогда не уйдет далеко от особой точки, то особая точка будет устойчивым состоянием равновесия, что соответствует устойчивому режиму функционирования системы.
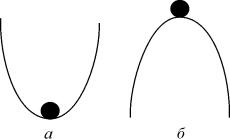
Строгое математическое определение устойчивости состояния равновесия уравнения dx/dt = f( x) выглядит следующим образом :
Состояние равновесия устойчиво по Ляпунову, если задав сколь угодно малое положительное 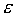
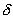
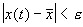
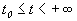
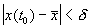
Иначе говоря, для устойчивого состояния равновесия справедливо утверждение: если в момент времени 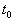
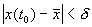
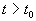
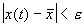
Другими словами: c тационарное состояние называется устойчивым, если малые отклонения не выводят систему слишком далеко из окрестности этого стационарного состояния. Пример — шарик в ямке (с трением или без трения).
Стационарное состояние называется асимптотически устойчивым, если малые отклонения от него со временем затухают. Пример — шарик в ямке в вязкой среде.
Стационарное состояние называется неустойчивым, если малые отклонения со временем увеличиваются. Пример: шарик на горке.
Устойчивое стационарное состояние представляет собой простейший тип аттрактора.
Аттрактором называется множество, к которому стремится изображающая точка системы с течением времени (притягивающее множество).
В нашем курсе мы рассмотрим следующие типы аттракторов:
· устойчивая точка покоя;
· предельный цикл — режим колебаний с постоянными периодом и амплитудой (начиная с размерности системы 2 );
· Области с квазистохастическим поведением траекторий в области аттрактора, например, «странный аттрактор» (начиная с размерности 3 ).
Аналитический метод исследования устойчивости стационарного состояния (метод Ляпунова). Линеаризация системы в окрестности стационарного состояния.
Метод Ляпунова приложим к широкому классу систем различной размерности, точечным системам, которые описываются обыкновенными дифференциальными уравнениями, и распределенным системам, описываемым уравнениями в частных производных, непрерывным и дискретным.
Рассмотрим метод линеаризации Ляпунова для одного автономного дифференциального уравнения первого порядка. Пусть 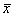
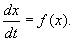
Пусть система, первоначально находившаяся в стационарном состоянии, отклонилась от него и перешла в близкую точку с координатой: 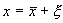

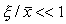
Перейдем в уравнении (2.1) от переменной x к переменной 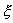
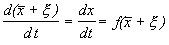
Учтем, что 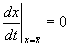
Правую часть разложим в ряд Тейлора в точке 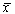
где
Отбросим члены порядка 2 и выше. Останется линейное уравнение:
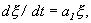
которое носит название линеаризованного уравнения или уравнения первого приближения. Интеграл этого уравнения для 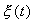
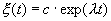
где 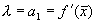
Если SYMBOL 108 f «Symbol» s 12 l SYMBOL 60 f «Symbol» s 12 0 , то при 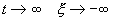
Если же SYMBOL 108 f «Symbol» s 12 l SYMBOL 62 f «Symbol» s 12 > 0 , то при 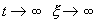
Если SYMBOL 108 f «Symbol» s 12 l =0 , то уравнение первого приближения не может дать ответа на вопрос об устойчивости состояния равновесия системы. Необходимо рассматривать члены более высокого порядка в разложении в ряд Тейлора. Такие случаи мы рассмотрим в лекции 6.
Аналогичные рассуждения проводятся при рассмотрении устойчивости стационарных состояний более сложных динамических систем.
Итак, устойчивость стационарного состояния 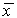
В случае одного уравнения вопрос об устойчивости состояния равновесия нетрудно решить, рассматривая график функции f(x).
По определению в стационарной точке правая часть уравнения (2.1) ‑ функция f(x) обращается в нуль.
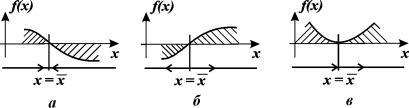
Здесь возможны три случая (рис. 2.4 а, б, в).
1. Вблизи состояния равновесия функция f(x) меняет знак с плюса на минус при возрастании x (рис. 2.4 а).
Отклоним изображающую точку системы в сторону 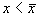
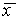
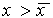
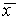
Рис. 2.4. Определение устойчивости стационарного состояния по графику функции f( x)
a – стационарное состояние 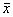
б, в ‑ стационарное состояние 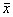
2. Вблизи состояния равновесия функция f ( x) меняет знак с минуса на плюс при возрастании x ( рис. 2.4 б) .
Проведите рассуждения, аналогичные случаю 1. Поместите изображающую точку в область 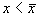
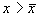
В обоих случаях изображающая точка удаляется от состояния равновесия. Стационарное состояние неустойчиво.
3. Вблизи состояния равновесия функции f(x) не меняет знак ( рис 2.4 в) .
Поскольку 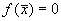
Вопрос. Является ли состояние равновесия в случае 3 устойчивым?
Ответ. Нет. По определению устойчивости.
1. Рост колонии микроорганизмов
За время D t прирост численности равен:
где R – число родившихся и S – число умерших за время SYMBOL 68 f «Symbol» s 12 D t особей пропорциональные этому промежутку времени:
В дискретной форме:
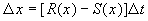
Разделив на SYMBOL 68 f «Symbol» s 12 D t и переходя к пределу при t SYMBOL 174 f «Symbol» s 12 ® 0 , получим дифференциальное уравнение
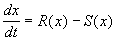
В простейшем случае, когда рождаемость и смертность пропорциональны численности:
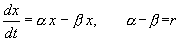
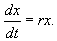
Разделим переменные и проинтегрируем:
Переходя от логарифмов к значениям переменной x и определяя произвольную постоянную С из начальных условий, получим экспоненциальную форму динамики роста.
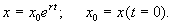
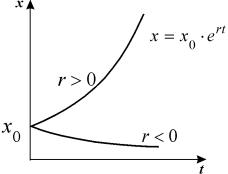
График функции (2.8) при положительных (размножение) и отрицательных (вымирание) значениях константы скорости роста представлен на рис. 2.5. Роль этой модели в развитии математической биологии и экологии мы обсудим в Лекции 3.
Рис. 2.5. Экспоненциальная форма динамики роста численности колонии микроорганизмов в соответствии с системой уравнений (2.7)

2. Вещество переходит в раствор
Пусть количество вещества, переходящего в раствор, пропорционально интервалу времени и разности между максимально возможной концентрацией Р и концентрацией x в данный момент времени: 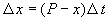
В форме дифференциального уравнения этот закон выглядит в
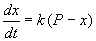
Разделим в этом уравнении переменные, и проинтегрируем:
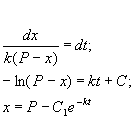
Здесь C 1 — произвольная постоянная. Если x (0) = 0,
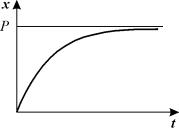
График этой функции представлен на рис. 2.6. – он представляет собой кривую с насыщением.
Рис. 2.6. Концентрация вещества х в зависимости от времени. График уравнения 2.9.

Какие дифференциальные уравнения можно решать аналитически?
Лишь для ограниченных классов дифференциальных уравнений разработаны аналитические методы решения. Подробно они изучаются в курсах дифференциальных уравнений. Отметим основные из них/
1. Уравнения с разделяющимися переменными решаются в интегралах. К ним относятся оба приведенные выше примера.
2. Линейные дифференциальные уравнения (не обязательно автономные).
3. Некоторые специальные виды уравнений.
Решение линейного уравнения
Линейным дифференциальным уравнением 1-го порядка называют уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид:
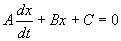
Здесь A, B, C — заданные непрерывные функции от t.
Пусть в некотором интервале изменения t A SYMBOL 185 f «Symbol» s 12 _ 0 . Тогда на него можно разделить все члены уравнения. При этом получим:
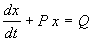
Eсли Q=0 , уравнение (2.12) называется однородным, если Q SYMBOL 185 f «Symbol» s 12 _ 0 – неоднородным.
Решим сначала однородное уравнение.
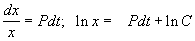
Общее решение линейного однородного уравнения имеет вид:
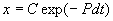
Чтобы найти решение неоднородного уравнения применим метод вариации постоянной. Будем считать С неизвестной функцией t . Подставляя правую часть выражения (2.13) в уравнение (2.12), имеем:
Теперь С находим интегрированием: 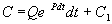
Итак, общее решение линейного неоднородного уравнения первого порядка:
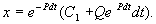
Таким образом, решение уравнения (2.12) представляет собой сумму двух слагаемых:
1) общее решение однородного уравнения (2.13) и
2) частное решение неоднородного уравнения, которое получается из общего решения, если С1 = 0.
Рассмотрим еще один пример, который относится к классическим моделям математической экологии. Логистическое уравнение было предложено Ферхюльстом в 1838 г. Оно имеет вид:
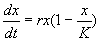
Это уравнение обладает двумя важными свойствами. При малых х численность х возрастает, при больших – приближается к определенному пределу К .
Уравнение (2.15) можно решить аналитически. Ход решения следующий. Произведем разделение переменных:
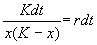
Представим левую часть в виде суммы и проинтегрируем
Переходя от логарифмов к переменным, получим:
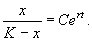
Здесь С – произвольная постоянная, которая определяется начальным значением численности x0 :
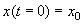
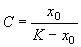
Подставим это значение С в формулу (2.17):
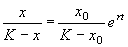
Отсюда получим решение – зависимость численности от времени:
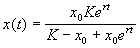
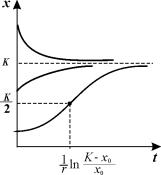
График функции (2.18) при разных начальных значениях численности популяции представлен на рис. 2.7.
Рис.2.7. Динамика численности в логистической модели 2.18
при разных начальных значениях численности

Если начальное значение х0 К/2, кривая роста имеет точку перегиба. Если х0 > К, численность со временем убывает.
В приведенных примерах в правой части уравнений стоят полиномы первой и второй степени. Если в правой части ‑ более сложная нелинейная функция, алгебраическое уравнение для стационарных значений может иметь несколько корней. Какое из этих решений реализуется в этом случае, будет зависеть от начальных условий.
В дальнейшем мы, как правило, не будем искать аналитическое решение для наших моделей. Для более сложных нелинейных уравнений это и невозможно. Однако важные заключения относительно свойств моделей можно сделать и на основании качественного их исследования, в первую очередь путем исследования устойчивости стационарных состояний и типов поведения системы вблизи этих состояний. При этом следует иметь в виду, что с помощью одного автономного дифференциального уравнения могут быть описаны только монотонные изменения переменной, и, следовательно, ни периодические, ни хаотические процессы не могут быть описаны. Для описания более сложного поведения необходимо либо переходить к системам большей размерности (2, 3 порядка и выше), либо вводить время в явном виде в правую часть уравнения. В Лекции 3 мы увидим, что дискретные уравнения и уравнения с запаздыванием могут описать и колебания, и динамический хаос.
Видео:Устойчивость 1 ОпределениеСкачать

Стационарные и нестационарные состояния
Вы будете перенаправлены на Автор24
Уравнение Шредингера вида:
описывает состояние движения микрочастицы, которое неизменно во времени и реализуется при постоянной энергии. Стационарными называют состояния, в которых все наблюдаемые физические величины не изменяются во времени. Надо отметить, что под движением в квантовой механике понимают изменений вообще, а не только перемещение. Движение связано не с пребыванием в стационарном состоянии, а изменением стационарного состояния. Состояние Вселенной в целом не является стационарным, но ее составные части (атомы, к примеру) могут находиться в стационарных состояниях. Но, если атомы находились бы в стационарном состоянии постоянно, и с ними не чего не происходило бы, то о них не было бы ни чего известно, мы не знали бы о их существовании. Так как существование атомов обнаруживается только тогда, когда они изменяют свое стационарное существование. В принципе, только данный переход интересует науку, а не сами стационарные состояния. И так, стационарные состояния никаких событий в физическом мире не представляют, но они дают возможность понять и сделать описание событий, которые происходят в мире. Стационарные состояния — фундамент описания физического мира.
Волновую функцию в стационарных состояниях можно определить как:
где $omega =frac$. При этом $Psileft(overrightarrowright)$ не зависит от времени.
При данном описании функции плотность вероятности не изменяется.
Основным свойством стационарного состояния является его единство. Частица принадлежит состоянию в целом, нельзя разделить состояние на части. Нельзя сказать, что при своем движении электрон проходит последовательно разные области пространства. В которых состояние его движения описывают, относящимися к этой области, значениями волновых функций $?.$ Так как невозможно соотнести движение частицы с пребыванием в разных областях пространства и нельзя представить единое во всем пространстве состояние его движения в отдельных частях пространства.
Из физических свойств стационарных состояний следуют математические требования к волновой функции ($Psi(x,y,z)$), которая описывает стационарные состояния.
Видео:Урок 455. Уравнение ШрёдингераСкачать

Математические требования к волновой функции
Волновая функция $Psi (x,y,z)$ является решением дифференциального уравнения (1). При этом $^2$ — плотность вероятности того, что частица находится в точке с координатами ($x,y,z$). Или $^2dxdydz$ — вероятность того, что частица находится в объеме $dxdydz$ в окрестности точки ($x,y,z$). Из сказанного выше следует, что волновая функция должна быть непрерывной, однозначной и конечной во всех точках. В том случае, если потенциальная энергия $Uleft(x,y,zright)$ — имеет поверхности разрыва непрерывности, то на таких поверхностях волновая функция $Psi$ и ее первая производная должны быть непрерывными. В областях пространства, где $Uleft(x,y,zright)$ становится бесконечной, волновая функция обращается в ноль. Свойство непрерывности требует, чтобы $Psileft(x,y,zright)$ на границе этой области была равна нулю. Кроме того плотность вероятности ($^2$) должна быть интегрируема.
Готовые работы на аналогичную тему
При строгом исследовании стационарных состояний выясняется, что они таковыми не являются. Но решения уравнения Шредингера приводят к существованию строго стационарных состояний, что противоречит результатам экспериментов. В этом проявляется ограниченность уравнений Шредингера, так как они не описывают радиационных переходов.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Нестационарные состояния
В общем случае, когда потенциальная энергия частицы зависит от времени, волновая функция равна $Psi=Psi(x,y,z,t)$ уравнение Шредингера имеет вид:
где $hbar =frac=1,05cdot ^Джcdot с $- постоянная Планка, $m$ — масса частицы, $Uleft(x,y,z,tright)$- потенциальная энергия частицы в силовом поле в котором перемещается частица, $triangle =frac+frac+frac$ — оператор Лапласа, $Psi=Psi(x,y,z,t)$ — волновая функция частицы, $i=sqrt$ — мнимая единица.
Уравнение (3) является справедливым для любой частицы, которая движется со скоростью много меньшей скорости света ($vll c, где c $— скорость света в вакууме). Уравнение (3) называют временн$acute$м уравнением Шредингера (общим уравнением), так как оно содержит производную от волновой функции по времени.
Задание: Временная часть уравнения Шредингера имеет вид: $hbar ifrac=EPsi.$ Каково решение данного уравнения?
Решение:
Проинтегрируем уравнение $frac=fracE Psi. $Разделим переменные:
Проведем интегрирование правой и левой частей выражения (1.1), получим:
Перейдем от логарифмов к функциям:
где $Psi_0=Psi_0left(0right)=const$- значение $Psi(t)$ в начальный момент времени $(t=0).$
Задание: Покажите, что если волновая функция циклически зависима от времени как:
$Psileft(x,tright)=Psi(x)e^<-fracEt>$, то плотность вероятности не зависит от времени.
Решение:
Плотность вероятности ($p$) определена как:
где $^2$ находят как произведение волновой функции ($Psi(x,t)$) на комплексно сопряженную величину $Psi^*(x,t)$):
Ответ: $p=Psi^2left(xright).$
Задание: Напишите уравнение Шредингера для линейного гармонического осциллятора. Считать, что сила упругости, которая действует на частицу, равна: $f=-kx$, где $k$ — коэффициент упругости, $x$ — смещение.
Решение:
За основу примем стационарное уравнение Шредингера:
Для линейного гармонического осциллятора, совершающего колебания по оси $X$ выражение (3.1) преобразуется к виду:
Потенциальная энергия $Uleft(xright)$ связана с силой упругости выражением:
Подставим полученное выражение (3.3) для $Uleft(xright)$ в уравнение (3.2), имеем:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 06 05 2021
🔥 Видео
Уравнение Шредингера Стационарные состоянияСкачать

Стационарные состояния.Квантовая физикаСкачать

6.3 Решение разностных уравненийСкачать

Квантовая механика 47 - Стационарное уравнение Шредингера. Гармонический осциллятор.Скачать

Чёрные дыры и молодые вселенные. Всё ли предопределенно на свете?Скачать

Вселенная от начала до черных дыр.Скачать

Откуда взялись темная материя и темная энергия?Скачать

Классические уравнения | одномерное стационарное уравнение ШрёдингераСкачать

Классические уравнения | одномерное стационарное уравнение Шрёдингера | беск. потенц. яма | 1Скачать

Классические уравнения | трёхмерное стационарное уравнение ШрёдингераСкачать

Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

Стационарное решение одномерного уравнения теплопроводности.Скачать

6. Особые решения ДУ первого порядкаСкачать

Классические уравнения | уравнение Шрёдингера (координатное представление) | простейший выводСкачать

Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать


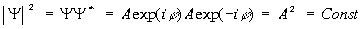
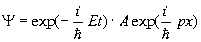
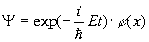
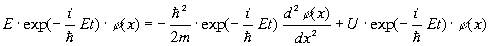
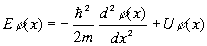
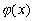 подчиняется уpавнению (3.20), котоpое мы пеpепишем в следующем виде:
подчиняется уpавнению (3.20), котоpое мы пеpепишем в следующем виде: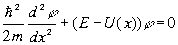
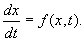
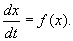 (2.1)
(2.1)