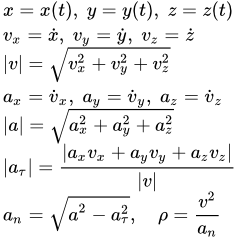- Введение
- Определение кинематических величин
- Пример решения задачи
- Определение скорости и ускорения точки по заданным уравнениям ее движения
- Решение
- Определение вида траектории
- Определение скорости точки
- Определение ускорения точки
- Определение остальных величин
- Как найти скорость из уравнения координаты
- ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
- Типовая задача «Уравнение координаты (нахождение неизвестной величины)»
- Типовая задача «Уравнение координаты. Движение двух тел»
- Типовая задача «График координаты»
- Типовая задача «График координаты. Движение нескольких тел»
- ЗАДАЧИ ПОСЛОЖНЕЕ
- Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение.
- Формула скорости
- Определение и формула скорости
- Скорость в разных системах координат
- Частные случаи формул для вычисления скорости
- Единицы измерения скорости
- Примеры решения задач
- 🔍 Видео
Видео:Уравнение координат при равноускоренном движенииСкачать

Введение
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы применим основные результаты этой теории к координатному способу задания движения материальной точки.
Пусть мы имеем неподвижную прямоугольную систему координат с центром в неподвижной точке . При этом положение точки M однозначно определяются ее координатами (x, y, z). Координатный способ задания движения точки – это такой способ, при котором заданы зависимости координат от времени. То есть заданы три функции от времени (при трехмерном движении):
Далее мы приводим формулы вычисления кинематических величин и пример решения задачи для координатного способа задания движения.
Видео:Физика - уравнения равноускоренного движенияСкачать

Определение кинематических величин
Зная зависимости координат от времени , мы автоматически определяем радиус-вектор материальной точки M по формуле:
,
где – единичные векторы (орты) в направлении осей x, y, z .
Дифференцируя по времени , находим проекции скорости и ускорения на оси координат:
;
;
Модули скорости и ускорения:
;
.
Единичный вектор в направлении касательной к траектории:
.
Его можно определить двумя способами – по направлению скорости, или в противоположную сторону. Поэтому здесь в знаменателе стоит не модуль скорости, а алгебраическая величина скорости, которая, по абсолютной величине, равна модулю скорости, но может принимать как положительные, так и отрицательные значения: . Она является проекцией скорости на направление единичного вектора .
Алгебраическая величина тангенциального (касательного) ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории:
.
Вектор тангенциального (касательного) ускорения:
.
Здесь также, как и для скорости, – это скалярная величина, которая может принимать как положительные так и отрицательные значения: .
Нормальное ускорение:
.
Вектор нормального ускорения:
; .
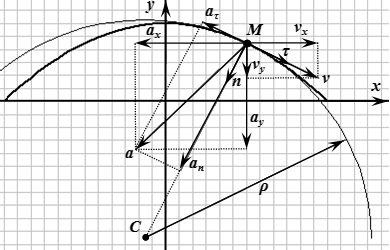
Единичный вектор в направлении главной нормали траектории (то есть единичный вектор, перпендикулярный касательной и направленный к центру кривизны траектории):
.
Здесь – это модуль нормального ускорения: . Нормальное ускорение всегда направлено к центру кривизны траектории. Оно не может быть направлено в противоположную сторону.
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Видео:Кинематика. Из координаты получаем скорость и ускорениеСкачать

Пример решения задачи
Определение скорости и ускорения точки по заданным уравнениям ее движения
По заданным уравнениям движения точки установить вид ее траектории и для момента времени найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Уравнения движения точки:
, см;
, см.
Решение
Определение вида траектории
Исключаем время из уравнений движения. Для этого перепишем их в виде:
; .
Применим формулу:
.
;
;
;
.
Итак, мы получили уравнение траектории:
.
Это уравнение параболы с вершиной в точке и осью симметрии .
Поскольку
, то
; или
.
Аналогичным образом получаем ограничение для координаты :
;
;
Таким образом, траекторией движения точки является дуга параболы
,
расположенная при
и .
Строим параболу по точкам.
| 0 | 6 |
| ± 3 | 5,625 |
| ± 6 | 4,5 |
| ± 9 | 2,625 |
| ± 12 | 0 |
Определяем положение точки в момент времени .
;
.
Определение скорости точки
Дифференцируя координаты и по времени , находим компоненты скорости.
.
Чтобы продифференцировать , удобно применить формулу тригонометрии:
. Тогда
;
.
Вычисляем значения компонент скорости в момент времени :
;
.
Модуль скорости:
.
Определение ускорения точки
Дифференцируя компоненты скорости и по времени , находим компоненты ускорения точки.
;
.
Вычисляем значения компонент ускорения в момент времени :
;
.
Модуль ускорения:
.
Алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории. Выберем направление совпадающим с направлением скорости . Тогда ; алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление скорости :
.
Поскольку , то вектор тангенциального ускорения направлен противоположно скорости .
Нормальное ускорение:
.
Вектор и направлен в сторону центра кривизны траектории.
Радиус кривизны траектории:
.
Траекторией движения точки является дуга параболы
; .
Скорость точки: .
Ускорение точки: ; ; .
Радиус кривизны траектории: .
Определение остальных величин
При решении задачи мы нашли:
вектор и модуль скорости:
; ;
вектор и модуль полного ускорения:
; ;
тангенциальное и нормальное ускорения:
; ;
радиус кривизны траектории: .
Определим остальные величины.
Единичный вектор в направлении касательной к траектории:
.
Вектор тангенциального ускорения:
.
Вектор нормального ускорения:
.
Единичный вектор в направлении главной нормали:
.
Координаты центра кривизны траектории:
.
Введем третью ось системы координат перпендикулярно осям и . В трехмерной системе
; .
Единичный вектор в направлении бинормали:
.
Автор: Олег Одинцов . Опубликовано: 22-02-2016 Изменено: 29-01-2020
Видео:Скорость и ускорение точки в полярных координатахСкачать

Как найти скорость из уравнения координаты
1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Типовая задача «Уравнение координаты (нахождение неизвестной величины)»
Задача № 1. В начальный момент времени тело находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.
Типовая задача «Уравнение координаты. Движение двух тел»
Задача № 2. Движение двух тел задано уравнениями x1 = 20 – 8t и х2 = –16 + 10t (время измеряется в секундах, координата — в метрах). Определите для каждого тела начальную координату, проекцию скорости, направление скорости. Вычислите время и место встречи тел.
Типовая задача «График координаты»
Задача № 3. Движение тела задано графиком координаты (зависимости координаты от времени). По графику определите: а) начальную координату тела; б) проекцию скорости тела; в) направление движения тела (по оси х или против оси х); г) запишите уравнение координаты.
Типовая задача «График координаты. Движение нескольких тел»
Задача № 4. На рисунке изображены графики движения трех тел. Изучив рисунок, для каждого тела определите: а) начальную координату; б) скорость; в) направление движения; г) запишите уравнение координаты.
ЗАДАЧИ ПОСЛОЖНЕЕ
Задача № 5. На рисунке представлены графики зависимости координаты х от времени t для пяти тел. Определите скорости этих тел. Проанализируйте точки пересечения графиков. Постройте графики зависимости скорости от времени.
РЕШЕНИЕ:
Задача № 6. По графикам на рисунке напишите уравнения движения x = x(t) . Из уравнений и графиков найдите координаты тел через 5 с , скорости движения тел, время и место встречи второго и третьего тел.
РЕШЕНИЕ:
Задача № 7. ОГЭ Расстояние ( S ) между городами М и К = 250 км . Одновременно из обоих городов навстречу друг другу выезжают автомашины. Машина из города М движется со скоростью = 60 км/ч , из города К — со скоростью ν2 = 40 км/ч . Построить график зависимости пути от времени для каждой из машин и по ним определить место встречи и время их движения до встречи.
Задача № 8. ЕГЭ Скорость течения реки vp = 1 м/с , скорость лодки относительно воды v0 = 2 м/с . Под каким углом к берегу следует держать курс, чтобы лодка двигалась перпендикулярно берегу? За какое время t она переправится через реку, ширина которой d = 200 м ?
Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение.
Задачи, описывающие движение, содержат два типа величин: векторные (имеющие направление) и скалярные (выражающиеся только числом). К векторным величинам при описании равномерного прямолинейного движения относятся скорость и перемещение.
Для перехода от векторов к скалярам выбирают координатную ось и находят проекции векторов на эту ось, руководствуясь следующим правилом: если вектор сонаправлен с осью, то его проекция положительна, если противоположно направлен — отрицательна. (Могут быть и более сложные случаи, когда вектор не параллелен координатной оси, а направлен к ней под некоторым углом.) Поэтому при решении задачи обязательно нужно сделать чертеж, на котором изобразить направления всех векторов и координатную ось. При записи «дано» следует учитывать знаки проекций.
При решении задач все величины должны выражаться в международной системе единиц (СИ), если нет специальных оговорок.
В решении задачи единицы величин не пишутся, а записываются только после найденного значения величины.
Это конспект по теме «ЗАДАЧИ на Прямолинейное равномерное движение с решениями». Выберите дальнейшие действия:
Видео:Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Формула скорости
Видео:Решение графических задач на равномерное движениеСкачать

Определение и формула скорости
Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора $bar$ точки по времени (t). Обозначают скорость обычно буквой v. Это векторная величина. Математически определение вектора мгновенной скорости записывается как:
Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения. Модуль скорости можно определить как первую производную от длины пути (s) по времени:
Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.
Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Скорость в разных системах координат
Проекции скорости на оси декартовой системы координат запишутся как:
Следовательно, вектор скоростив декартовых координатах можно представить:
где $bar, bar, bar$ единичные орты. При этом модуль вектора скорости находят при помощи формулы:
В цилиндрических координатах модуль скорости вычисляют при помощи формулы:
в сферической системе координат:
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Частные случаи формул для вычисления скорости
Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const). При равномерном движении скорость можно вычислить, применяя формулу:
где s– длина пути, t – время, за которое материальная точка преодолела путь s.
При ускоренном движении скорость можно найти как:
Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:
где $bar_0$ – начальная скорость движения, $bar = const$ .
Видео:уравнение координаты материальной точки при равноускоренном движенииСкачать

Единицы измерения скорости
Основной единицей измерения скорости в системе СИ является: [v]=м/с 2
Видео:Уравнение движенияСкачать

Примеры решения задач
Задание. Движение материальной точки А задано уравнением: $x=2 t^-4 t^$ . Точка начала свое движение при t0=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.
Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:
Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент времении сравним результат с нулем:
Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.
Ответ. Против оси X.
Задание. Скорость материальной точки является функцией от времени вида:
где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии 10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.
Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:
Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:
Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:
$$ begin 10 t-t^=10(2.2) \ t_=5+sqrt approx 8,8(c) ; t_=5-sqrt approx 1,13(c) end $$
Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:
При решении уравнения (2.3) нам подойдет корень равный:
Ответ. 1) $x=0 mathrm<
m>$ 2) $t_=8,8 mathrm, t_=1,13 c, t_=11 c$
🔍 Видео
Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Как найти проекцию вектора скорости и ускорения. Выполнялка 112Скачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Кинематика. Практика 1 - Уравнения координаты и скоростиСкачать

Траектория и уравнения движения точки. Задача 1Скачать

Определение координаты движущегося тела | Физика 9 класс #3 | ИнфоурокСкачать

Равномерное прямолинейное движение - физика 9Скачать

Урок 12. Равномерное прямолинейное движениеСкачать