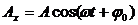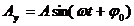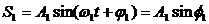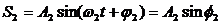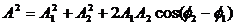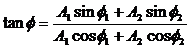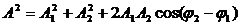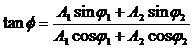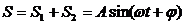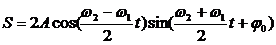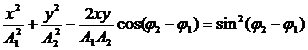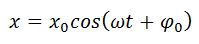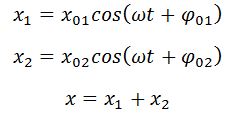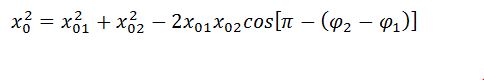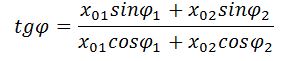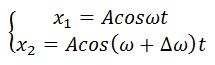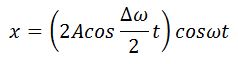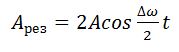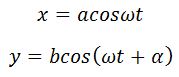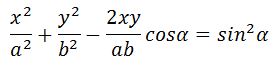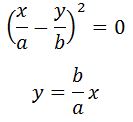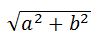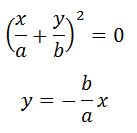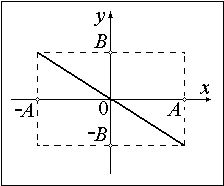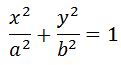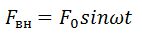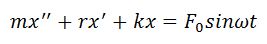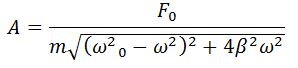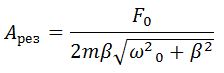Как найти результирующее уравнение колебаний (3 видео)

Сложение гармонических колебаний

Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача — найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний — нахождение траектории результирующего колебания.

Содержание

Метод векторных диаграмм
Сложение колебаний
Сложение колебаний направленных по одной прямой
Суперпозиция взаимно перпендикулярных колебаний
Примеры задач на сложение колебаний
Как найти результирующее уравнение колебаний
🔥 Видео

Видео:Выполнялка 53.Гармонические колебания.Скачать

Метод векторных диаграмм

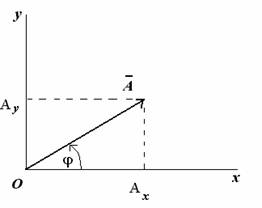
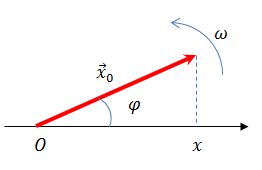
Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А. Очевидно, что угол j = w t + j₀ где j₀ — начальный угол.

Проекции вектора А на оси координат запишутся:

Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу — начальную фазу.

Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:

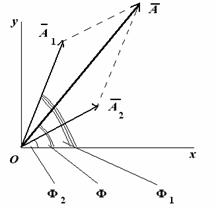
Сопоставим этим колебаниям два вектора А₁ и А₂, вращающихся с соответствующими угловыми скоростями.

Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f (фаза результирующего колебания).

Из очевидных геометрических соображений находим:

Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то 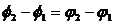, то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:

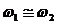
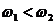
Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть , и пусть для определенности . Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний

получим уравнение суммарного колебания:

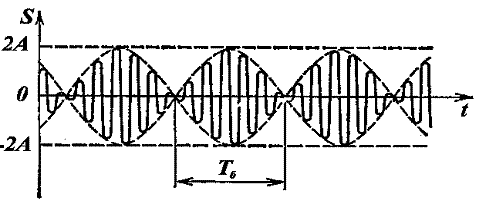
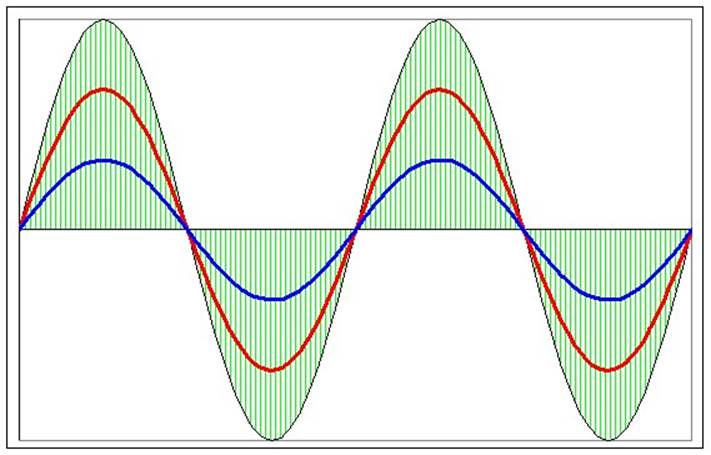
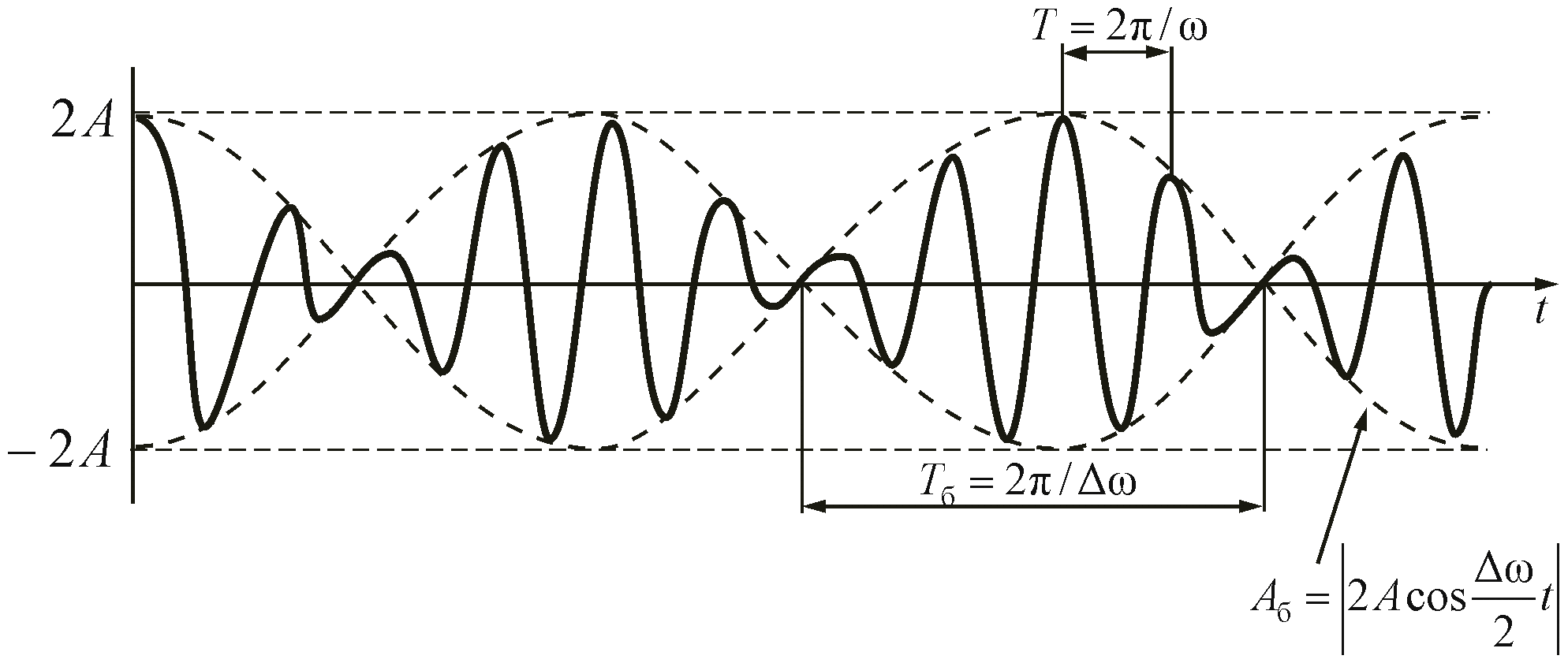
Полученное результирующее колебание не является гармоническим (сравни с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.

Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот 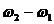— частотой биений (циклической).

При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).

например, сложим два колебания с одинаковыми частотами:

исключив время, получим:

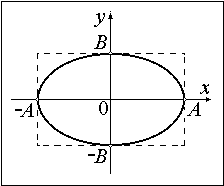
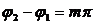
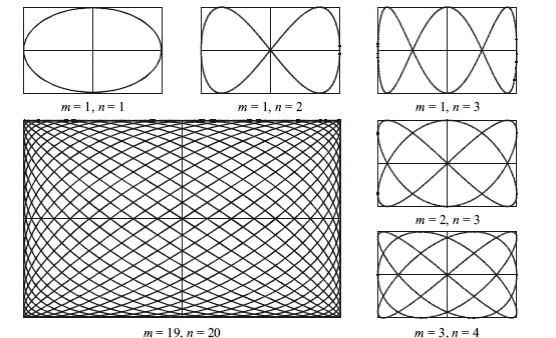
В общем случае это — уравнение эллипса. При A₁=A₂ — окружность, при (m — целое) — отрезок прямой.

Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу.

Видео:67. Сложение колебанийСкачать

Сложение колебаний

Тело, совершающее колебания, способно принимать участие в нескольких колебательных процессах одновременно. В таком случае возникает необходимость выяснить, каким будет результирующее колебание.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Сложение колебаний направленных по одной прямой

Рассмотрим сложение двух гармонических колебаний одинакового направления и равной частоты. Тогда смещение ($x$) совершающего колебания тела будет равно сумме смещений $x_1$ и $x_2$, которые представим в виде уравнений:

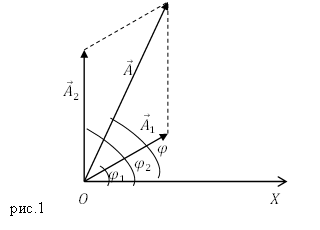
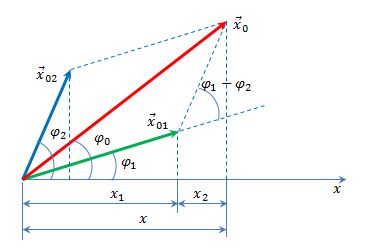
Колебания (1) и (2) представим на векторной диаграмме в виде векторов $_1$ и $_2$ (рис.1).

Из рис.1 видно, что амплитуду результирующего колебания можно найти как:

где $A_1$; $A_2$ — амплитуды сложенных колебаний; $_2;;_1$ — начальные фазы суммирующихся колебаний. При этом начальную фазу полученного колебания ($varphi $) вычисляют, применяя формулу:

Из выражения (4) видно, что если $_2-_1=0$, тогда получим колебание, амплитуда которого равна:

При разности фаз равной $_2-_1=pm pi $, что означает, что колебания находятся в противофазе, амплитуда сложенных колебания составляет:

Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Суперпозиция взаимно перпендикулярных колебаний

Пусть у нас происходят два взаимно перпендикулярные гармонические колебания с одной частотой $_0$. Колебания происходят вдоль осей X и Y. Пусть начало отсчета времени было таким, что начальная фаза первого колебания равнялась нулю. При этом уравнения колебаний предстанут в виде:

Уравнения (8) и (9) вместе представляют уравнение траектории движения точки в параметрическом виде. Исключаем время из уравнений, получаем уравнение траектории:

Уравнение траектории точки, которая принимает участие в перпендикулярных колебаниях с амплитудами $A_1$и $A_2$ и начальными фазами $_2и_1$:

Уравнение (10) — это уравнение эллипса.

В случае равенства начальных фаз составляющих колебаний уравнение траектории преобразуется к виду:

что говорит о движении точки по прямой линии. Точка, совершающая гармонические колебания движется по этой прямой, расстояние от начала координат до точки равно:

Если $Delta varphi =_2-_1=frac,$ уравнением траектории становится выражение:

что означает, траектория движения эллипс.

Если частоты нормальных друг другу колебаний отличны на очень небольшую величину $Delta omega $, то их рассматривают как колебания с равными частотами, но переменной разностью фаз. При этом суммарное движение проходит по медленно изменяющей вид кривой.

Траектории движений суперпозиций взаимно нормальных колебаний с разными частотами представляют собой сложные кривые, которые называют фигурами Лиссажу.

Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Примеры задач на сложение колебаний

Задание. Какова разность фаз суммируемых колебаний, если складывались два колебания, направленных по одной прямой, обладающих одинаковыми амплитудами и периодами? Сложились они в колебание той же амплитуды.

Решение. В качестве основы для решения задачи используем выражение для вычисления амплитуды складывающихся колебаний, если они направлены вдоль одной прямой:

Учитывая условия задачи выражение (1.1) преобразуем к виду:

Выразим из (1.2) искомую разность фаз:

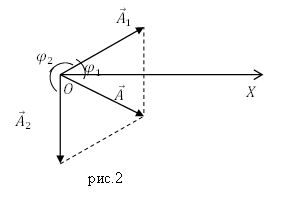
Изобразим векторную диаграмму колебаний (рис.2).

Ответ. $Delta varphi =fracилиfrac$

Задание. Материальная точка совершает одновременно два взаимно перпендикулярных колебания: $x=A<cos left(_0tright) >,y=B<cos left(_0tright) >,$ каким будет уравнение траектории движения точки?

Решение. Из уравнения:

Подставим правую часть выражения (2.2) вместо $<cos left(_0tright) >$ в формулу:

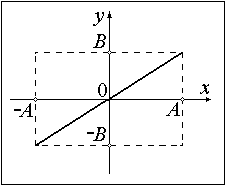
Уравнением движения точки будет прямая линия.

Ответ. $y=frac x$

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Как найти результирующее уравнение колебаний

Сложение нескольких гармонических колебаний становится наглядней, если изображать колебания в виде векторов на плоскости. Полученная таким образом схема называется векторной диаграммой .

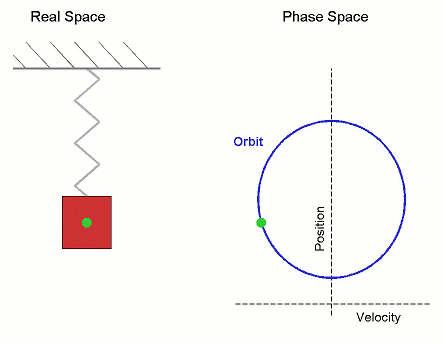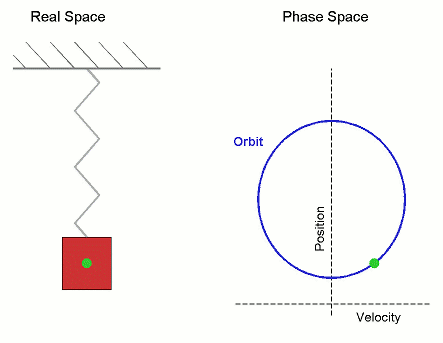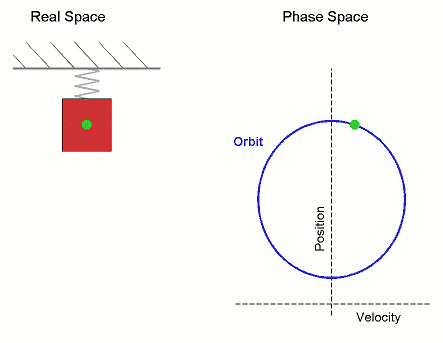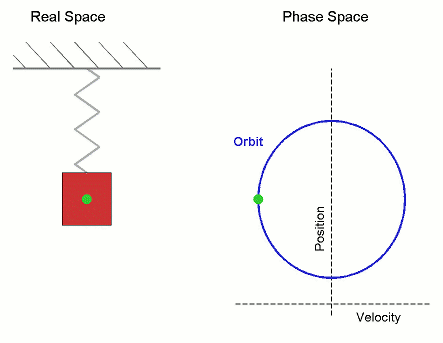
Тогда координата проекции вектора изменяется со временем по закону

Гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебаний, направление вектора образует с осью х угол, равный начальной фазе колебаний, а угловая скорость вращения вектора равна его циклической частоте.

Сложение двух гармонических колебаний одинакового направления и одинаковой частоты

Смещение х колеблющегося тела будет равно сумме смещений х₁ и х₂:

Вектор х₀ представляет собой результирующую амплитуду колебаний. Он вращается с той же угловой скоростью ω и начальной фазой φ₀.

Рассмотрим частные случаи.

φ₁ — φ₂

х = х₁ + х₂

Если оба колебания находятся в противофазе (разность фаз равна ±π), то результирующая амплитуда х = |х₁ — х₂|.

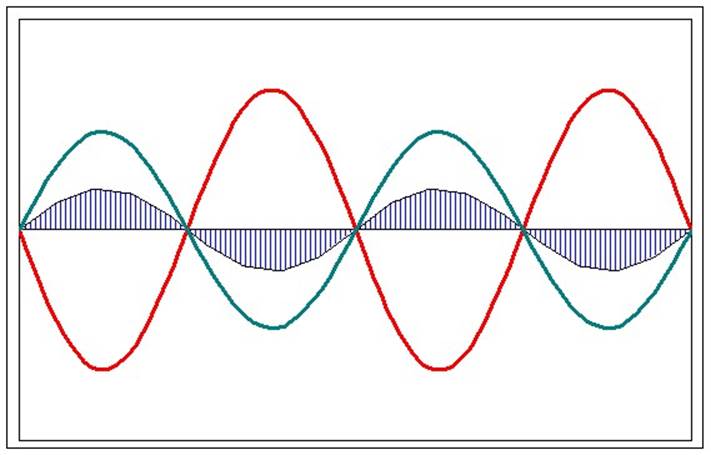
Как найти результирующее уравнение колебаний

Если частоты неодинаковы, то векторы будут вращаться с различной скоростью. Результирующий вектор пульсирует по величине и вращается с непостоянной скоростью.

Биения

Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биением .

Пусть два колебания мало отличаются по частоте. Тогда амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω намного меньше ω. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

Тогда результирующее колебание можно представить в виде:

Амплитуда результирующего колебания меняется со временем по закону

Сложение взаимно перпендикулярных колебаний

Допустим, что материальная точка может совершать колебания как вдоль оси х, так и вдоль перпендикулярной к ней оси у. Если возбудить оба колебания, материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.

Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний запишутся следующим образом:

где α — разность фаз обоих колебаний.

После преобразования получим уравнение траектории, которое представляет собой параметрическое уравнение эллипса, оси которого повернуты относительно осей х и у.

Рассмотрим частные случаи.

1. Разность фаз равна нулю. В этом случае получается уравнение прямой.

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой

2. Разность фаз равна ±π. Уравнение имеет вид прямой.

3. При α = ±π/2 получается уравнение эллипса, приведенного к координатным осям. При равенстве амплитуд эллипс превращается в окружность.

При сложении взаимно перпендикулярных колебаний разных частот получаются различные траектории материальной точки, названные фигурами Лиссажу. Чем ближе отношение частот к единице, тем сложнее получается фигура Лиссажу.

Резонанс

Резонанс — явление резкого возрастания амплитуды вынужденных колебаний при совпадении частот вынуждающей силы и собственных колебаний маятника. Вынужденные колебания происходят, если внешняя сила изменяется периодически:

Дифференциальное уравнение вынужденных колебаний

Амплитуда колебания определяется формулой

где коэффициент затухания β = r/2m.

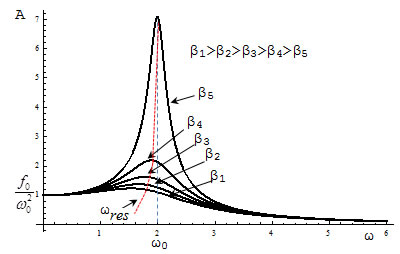
Для определения резонансной частоты надо найти минимум знаменателя. Резонансная амплитуда

Автоколебания

При затухающих колебаниях энергия системы расходуется на преодоление сил сопротивления. Если восполнять эти потери, то колебания станут незатухающими. Если система сама управляет воздействием внешних сил, то такое колебательное движение называется автоколебанием.

В автоколебательной системе обязательно присутствуют элементы:

сама колебательная ситема, ее параметры определяют частоту автоколебаний;
источник энергии, поддерживающий автоколебания;
клапан, регулирующий поступление энергии;
механизм обратной связи, посредством которой система управляет клапаном так, чтобы поступающая энергия компенсировала потери за счет трения и сопротивления среды.