Как найти расстояние от вектора до подпространства заданного уравнением

Видео:Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:18. Расстояние от точки до прямой в пространствеСкачать

Вычисление расстояний между геометрическими объектами

Видео:7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

Линейные многообразия

Видео:Как разложить вектор по базису - bezbotvyСкачать

Расстояние от точки до линейного многообразия (плоскости)

Задача. Найти расстояние от точки $ X_ in ^ $ до линейного многообразия (плоскости) $ mathbb M $ в $ ^ $, заданного системой уравнений $$ left< begin c_x_1+c_x_2+dots+c_x_n &=& h_1 \ dots & & dots \ c_x_1+c_x_2+dots+c_x_n &=& h_m end right. $$ или, в матричном виде $$ CX= quad npu quad C=left( begin c_& c_ & dots & c_ \ dots & & & dots \ c_& c_ & dots & c_ end right)_ , =left( begin h_1 \ vdots \ h_m end right), X=left( begin x_1 \ x_2 \ vdots \ x_n end right) $$ При этом предполагается, что $ mle n_ $ и что ранг матрицы $ C_ $ равен $ m_ $, то есть система уравнений совместна и определяемое ею многообразие в $ ^ $ является $ (n-m)_ $-мерным.

Теорема 1. [1]. Составим квадратную матрицу порядка $ m+1_ $:

$$ M=left( begin Ccdot C^ & CX_0- \ (CX_0- )^ & 0 end right) $$ Расстояние от точки $ X_ $ до линейного многообразия $ mathbb M $ вычисляется по формуле $$ d= sqrt<-frac<det(Ccdot C^)>> . $$

Доказательство ☞ ЗДЕСЬ.

Расстояние от точки $ X_=(x_,dots,x_)^ $ до гиперплоскости (или, в случае $ n=2 $, прямой)

$$ c_1x_1+dots+c_nx_n= h $$ равно $$ d= frac<|c_1x_+dots+c_nx_-h|><sqrt> . $$ Ближайшая к $ X_0 $ точка гиперплоскости: $$ X_=X_0- frac<c_1x_+dots+c_nx_-h> left(begin c_1 \ vdots \ c_n end right) , . $$

Пусть теперь линейное многообразие (плоскость) задано параметрически $$ mathbb M= < Y_0+lambda_1 Y_1+dots+lambda_k Y_k quad mid quad subset > $$ при фиксированных столбцах $$ subset ^n . $$ Предположим, что эти столбцы линейно независимы. Составим из них матрицы $$ L=left[ Y_1|dots|Y_k right]_ quad u quad tilde L = left[ Y_1|dots|Y_k| X_0-Y_0 right]_ $$ (здесь $ |_ $ означает конкатенацию).

Теорема 2. Расстояние $ d_ $ от точки $ X_ $ до линейного многообразия $ mathbb M $ вычисляется по формуле

Доказательство. Утверждение теоремы 2 является частным случаем общего результата о вычислении расстояния от точки до линейного многообразия в евклидовом пространстве. ♦

Теорема 3. Ближайшая к точке $ X_0 $ точка многообразия $ mathbb M_ $ (проекция точки на многообразие) определяется по формуле

Доказательство ☞ ЗДЕСЬ.

Пример. Найти расстояние от точки $ X_=(1,1,1,1)^ $ до плоскости

Решение. 1-й способ: применение теоремы 1. Имеем: $$ C=left( begin 3 & 1 & -1 & 1 \ 1 & -2 & 1 & 2 end right), = left( begin 1 \ 2 end right), $$ $$ Ccdot C^ = left( begin 12 & 2 \ 2 & 10 end right), CX_0=left( begin 4 \ 2 end right), CX_0-=left( begin 3 \ 0 end right) , $$ $$ frac<left| begin 12 & 2 & 3 \ 2 & 10 & 0 \ 3 & 0 & 0 end right|><left| begin 12 & 2 \ 2 & 10 end right|>=frac=-frac . $$

2-й способ: применение теоремы 2. Общее решение системы уравнений, задающей плоскость: $$ x_3=fracx_1+fracx_2, x_4=1-fracx_1+fracx_2 . $$ Таким образом, плоскость может быть представлена в параметрическом виде $$ Y_0+lambda_1 Y_1 + lambda_2 Y_2 quad npu quad Y_0 = left( begin 0 \ 0 \ 0 \ 1 end right), Y_1=left( begin 0 \ 3 \ 4 \ 1 end right), Y_2=left( begin 3 \ 0 \ 5 \ -4 end right) . $$ Имеем: $$ L= left( begin 0 & 3 \ 3 & 0 \ 4 & 5 \ 1 & -4 end right), tilde L =left( begin 0 & 3 & 1 \ 3 & 0 & 1 \ 4 & 5 & 1 \ 1 & -4 & 0 end right), frac<left| begin 26 & 16 & 7 \ 16 & 50 & 8 \ 7 & 8 & 3 end right|><left| begin 26 & 16 \ 16 & 50 end right|>=frac=frac . $$ Координаты ближайшей точки к $ X_ $: $$ X_= left(begin 1 \ 1 \ 1 \ 1 endright)+left( begin 0 & 3 \ 3 & 0 \ 4 & 5 \ 1 & -4 end right)left( begin 26 & 16 \ 16 & 50 \ end right)^ left(begin 0 & 3 & 4 & 1 \ 3 & 0 & 5 & -4 end right)left(begin 1 \ 1 \ 1 \ 0 endright)=frac left(begin 16 \ 37 \ 76 \ 49 endright) , . $$

Ответ. $ d=sqrt approx 0.8808303295 $.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Расстояние между линейными многообразиями (плоскостями)

Пусть линейные многообразия в $ ^ $ заданы параметрически $$ mathbb M_1= < X_0+ lambda_1 X_1+dots + lambda_k X_k mid subset mathbb R > ; $$ $$ mathbb M_2=< Y_0+mu_1Y_1+dots+mu_Y_ mid <mu_1,dots,mu_> subset mathbb R > $$ при фиксированных столбцах $$ <X_0,X_1,dots,X_k,Y_0,Y_1,dots,Y_>subset ^n . $$ Составим из этих столбцов матрицы $$ P=left[ X_1|dots|X_k| Y_1|dots | Y_ right]_ quad u quad tilde P = left[ X_1|dots|X_k| Y_1|dots | Y_| X_0-Y_0 right]_ $$ (здесь $ |_ $ означает конкатенацию).

Теорема. Расстояние между линейными многообразиями $ mathbb M_1 $ и $ mathbb M_2 $ вычисляется по формуле

Пример. [2]. Найти расстояние между плоскостями

$$ left( begin 89 \ 37 \ 111 \ 13 \54 end right) + lambda_1 left( begin 1 \ 1 \ 0 \ -1 \ -1 end right) + lambda_2 left( begin 1 \ -1 \ 0 \ -1 \ 1 end right) quad mbox quad left( begin 42 \ -16 \ -39 \ 71 \3 end right) + mu_1 left( begin 1 \ 1 \ 0 \ 1 \ 1 end right) + mu_2 left( begin 1 \ -1 \ 0 \ 1 \ -1 end right) . $$

Решение. $$ P^cdot P=4cdot E_, quad tilde P^cdot tilde P= left(begin 4 & 0 & 0 & 0 & 107 \ 0 & 4 & 0 & 0 & 103 \ 0 & 0 & 4 & 0 & 93\ 0 & 0 & 0 & 4 & -115 \ 107 & 103 & 93 & -115 & 33483 end right) . $$

Ответ. $ d=150_ $.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Квадратичные многообразия (квадрики)

В последующих пунктах, касающихся вычисления расстояний между геометрическими объектами, хотя бы один из которых представлен квадратным уравнением, используется следующая идеология решения. Первоначальной целью ставится построение уравнения расстояний, т.е. алгебраического уравнения от одной переменной, среди корней которого находится квадрат искомого расстояния. После нахождения этого корня, координаты ближайшей точки (или пары ближайших точек) находятся в виде рациональных функций от величины квадрата расстояния. Таким образом, мы «переворачиваем» традиционную схему решения оптимизационных задач:

стационарные точки $ rightarrow $ критические значения

Такая реверсия традиционного подхода оправдана, с одной стороны, тем, что задача сводится к одномерной — поиску корней полинома от одной переменной. Причем нас будет интересовать, как правило, единственный корень этого полинома — минимальный положительный. С другой стороны, уравнение расстояний удается построить в результате чисто алгебраической процедуры: конечного числа элементарных алгебраических операций над коэффициентами уравнений, задающих многообразия. Алгоритм основан на аппарате исключения переменных в системах нелинейных алгебраических уравнений, и ключевым объектом в нем оказывается вычисление дискриминанта полинома (от одной или двух переменных).

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Расстояние от точки до квадрики

Теорема 1. Пусть квадрика в $ ^ $, задана уравнением

$$ X^AX+2B^X-1=0 , (A=A^) . $$ Квадрат расстояния до нее от не лежащей на ней точки $$ X_ in ^, quad ( X_0^AX_0+2 B^X_-1ne 0 ) $$ равен минимальному положительному корню уравнения расстояний $$ (z)=0 quad npu quad (z)=_ left( Phi(mu,z) right) . $$ Здесь $$ Phi(mu,z)=det left( left[ begin A & B \ B^ & -1 end right] + mu left[ begin -E & X_0 \ X_0^ & z-X_0^X_0 end right] right), $$ $ _ $ означает дискриминант полинома $ Phi(mu,z) $, рассматриваемого относительно переменной $ mu_ $, а $ E_ $ — единичная матрица порядка $ n_ $. Дополнительно предполагается, что указанный корень не является кратным.

[3]. Квадрат расстояния от начала координат $ in ^ $ до квадрики в $ ^ $, заданной уравнением

$$ X^AX+2,B^X-1=0 , $$ равен минимальному положительному корню уравнения расстояний $$ (z)=0, quad npu quad (z)=_ left( f(mu)(mu z-1)-B^q(A,mu)B right) , $$ и при условии, что указанный корень не является кратным. Здесь $ f(mu_)=det (A-mu E) $ — характеристический полином матрицы $ A_ $, а $ q(A,mu)_ $ — матрица взаимная матрице $ A-mu E_ $.

В частном случае $ B=_ $ (квадрика центрирована к началу координат), имеем:

$$ (z)=left[z^nf(1/z) right]^2_(f(mu)) , $$ и расстояние от начала координат до квадрики оказывается равным $ 1/sqrt<lambda_^> $, где $ lambda_^ $ — максимальное собственное число матрицы $ A_ $.

Пример. Найти расстояние от начала координат до эллипсоида

Решение. Здесь $$A = left( <begin frac & -frac & 0 \ && \ -frac & frac & -frac \ && \ 0 & -frac & frac end> right),quad B = left( begin -frac \ \ -frac \ \ frac end right) ,$$ $$ f(mu)=det (A-mu E)=-mu ^ + mu ^ — frac mu + frac $$ Матрица взаимная матрице $ A-mu E_ $: $$ q(A, mu)= left( begin mu ^ — frac mu + frac & — frac mu + frac & frac \ && \ — frac mu + frac & mu^2 -fracmu+frac & — frac mu +frac \ && \ frac & — frac mu + frac & mu ^ — fracmu+frac end right) . $$ $$ Phi(mu,z)=f(mu)(mu z-1)-B^q(A,mu)B= $$ $$ =-z mu ^ + (z+1) mu ^ + left(-frac z — fracright) mu ^ +left( frac z + frac right) mu — frac . $$ Воспользуемся детерминантным представлением дискриминанта: $$ (z) = _ (Phi(mu,z)) = frac times $$ $$ times left| begin 4z & — 3z-3 & fracz + frac & — frac z — frac & 0 & 0 \ &&&&& \ 0 & 4z & — 3z-3 & frac z + frac & — frac z — frac & 0 \ &&&&& \ 0 & 0 & 4z & — 3z-3 & fracz + frac & — frac z — frac \ &&&&& \ 0 & 0 & — z — 1 & fracz + frac & — frac z — frac & frac \ &&&&& \ 0 & — z — 1 & fracz + frac & — fracz — frac & frac & 0 \ &&&&& \ — z — 1 & frac z + frac & — frac z — frac & frac & 0 & 0 end right| = $$ $$ =2^3^ ( 38263752,z^6-966487788,z^5+9376985736,z^4-43882396481,z^3+$$ $$ +102982092872,z^2-116747905827,z+50898162294) quad . $$ Вещественные корни уравнения расстояний: $$ z_1approx 1.394685, z_2 approx 5.701814, z_3 approx 7.043941, z_4 approx 7.590060 . $$

Ответ. $ d= sqrt approx 1.180968 $.

Нахождение точки на квадрике, ближайшей к заданной точке $ X_ $, возможно с помощью следующего результата.

Теорема 2. При выполнении условий теоремы 1, координаты точки $ X_ $ квадрики, ближайшей к точке $ X_ $ находятся по формуле

$$ X_=-A^ B — mu_ (A -mu_E)^ (A^ B+X_0)=(mu_E- A)^ (B+mu_ X_0) . $$ Здесь $ mu_ $ означает кратный корень полинома $ Phi(mu,z_) $, где полином $ Phi(mu,z) $ берется из формулировки теоремы 1, а $ z_^ $ означает минимальный положительный корень уравнения расстояний.

Этот результат требует пояснений. Итак, поскольку дискриминант полинома $ Phi(mu,z_) $ обращается в нуль, то у этого полинома — как полинома по $ mu_ $ — имеется кратный корень $ mu =mu_ $. Можно доказать [4], что при условии простоты корня $ z=z_ $ уравнения расстояний $ mathcal F(z)=0 $ кратность корня $ mu =mu_ $ для полинома $ Phi(mu,z_) $ будет равна ровно $ 2_ $, и других кратных корней этот полином не имеет. Но тогда, выражение для $ mu_^ $ может быть найдено в виде рациональной функции коэффициентов полинома $ Phi(mu,z_) $. Последнее утверждение может быть доказано разными способами, и в качестве самого наглядного выберем тот, что основан на свойствах дискриминанта, например, на том, что изложено ☞ ЗДЕСЬ.

При выполнении условия предыдущей теоремы, координаты точки $ X_^ $, ближайшей на квадрике к точке $ X_ $, являются рациональными функциями от квадрата расстояния.

Точка $ X_ $ квадрики $ X^AX+2,B^X-1=0 $, ближайшая к началу координат $ X_0= mathbb O $, находится по формуле:

$$ X_ = — frac<f(mu_)> q(A,mu_) B . $$ Здесь $ f(mu_)=det (A-mu E) $ — характеристический полином матрицы $ A_ $, $ q(A,mu)_ $ — матрица взаимная матрице $ A-mu E_ $, а $ mu_ $ означает кратный корень уравнения $$f(mu)(mu z_-1)-B^q(A,mu)B=0 , $$ где $ z_^ $ — величина квадрата расстояния от $ mathbb O_ $ до квадрики.

Пример. Найти ближайшую к началу координат точку эллипсоида из предыдущего примера.

Решение. Подставляем $ z_=z_ approx 1.394685 $ в формулу для определения кратного корня, т.е. в отношение двух конкретных миноров детерминантного представления дискриминанта: $$ mu=-frac<left| begin 4z & — 3z-3 & frac z + frac & 0 \ &&& \ 0 & 4z & — 3z-3 & — frac z — frac \ &&& \ 0 & — z — 1 & fracz + frac & frac \ &&& \ — z — 1 & fracz + frac & — fracz — frac & 0 end right|> <left| begin 4z & — 3z-3 & frac z + frac & — frac z — frac \ &&& \ 0 & 4z & — 3z-3 & fracz + frac \ &&& \ 0 & — z — 1 & fracz + frac & — fracz — frac \ &&& \ — z — 1 & fracz + frac & — fracz — frac & frac end right|> $$ получаем $ mu_^ approx 0.572670 $. Подставляем это значение в формулу для определения $ X_^ $ из последнего следствия: $$ X_approx left(begin 0.071171 \ -0.867719 \ 0.797924 end right) . $$

Проверка. Если подставить вместо $ X_ $ его приближенное значение, то получим: $$ X_^ X_ approx mathbf4, X_^AX_+2,B^X_-1 approx 2.9cdot 10^ , $$ и вектор $ X_ $ перпендикулярен эллипсоиду в точке $ X_=X_ $: $$ AX_+B approx left(begin 0.040757\ -0.496917 \ 0.456948 end right)approx mu_ X_ . $$

Видео:Расстояние от точки до прямойСкачать

Расстояние от линейного многообразия (плоскости) до квадрики

Задача. Найти расстояние от эллипсоида в $ ^ $, заданного уравнением $$ X^AX+2B^X-1=0 , (A=A^) $$ до линейного многообразия (плоскости) в $ ^ $, заданной системой уравнений $$ left< begin c_x_1+c_x_2+dots+c_x_n &=& 0 \ dots & & dots \ c_x_1+c_x_2+dots+c_x_n &=& 0 end right. iff CX= quad npu quad C=left( begin c_& c_ & dots & c_ \ dots & & & dots \ c_& c_ & dots & c_ end right)_ $$ При этом предполагается, что $ mle n_ $ и что ранг матрицы $ C_ $ равен $ m_ $, т.е. определяемая системой плоскость в $ ^ $ является $ (n-m)_ $-мерной.

Теорема. [3]. Необходимое и достаточное условие того, что линейное многообразие (плоскость) пересекает эллипсоид зависит от знакоопределенности матрицы $ A_ $:

Условие равенства нулю определителя из теоремы является необходимым и достаточным для существования точки касания эллипсоида и плоскости.

Теорема. [3]. Если условие предыдущей теоремы не выполняется, то квадрат расстояния от эллипсоида до плоскости совпадает с минимальным положительным корнем полинома

$$ (z) =_mu left( mu^m left| begin A & B & C^\ B^ & -1 + mu z & mathbb\ C & mathbb & frac C cdot C^ end right| right), $$ в предположении, что этот корень не является кратным. Здесь $ _ $ — дискриминант полинома, рассматриваемого относительно переменной $ mu_ $.

Если строки матрицы $ C_ $ ортонормированны, то преобразованием определителя в теореме можно понизить его порядок: выражение под знаком дискриминанта можно преобразовать в

Пример. Найти расстояние от оси $ x_ $ до эллипсоида

$$ 7, x_1^2+6, x_2^2 +5, x_3^2 -4,x_1x_2-4,x_2x_3-37,x_1-12,x_2+3,x_3+54=0 . $$

Решение. Здесь $$ A= left( begin -frac & frac & 0 \ &&\ frac & -frac & frac \ &&\ 0 & frac & -frac end right), B=left( begin frac \ \ frac \ \ -frac end right) $$ и можно взять $$ C= left( begin 0 & 1 & 0 \ 0 & 0 & 1 end right) . $$ Матрица $ A_ $ отрицательно определена, условие пересечения прямой и эллипсоида не выполняется: $$ left| begin A & B & C^\ B^ & -1 & \ C & & mathbb end right| times (-1)^3 = — frac

Расстояния в $ ^ $ от плоскости

$$ c_1x_1+dots+c_nx_n = h iff CX=h $$ до ближайшей и до самой дальней точек эллипсоида $$ X^AX+2B^X-1=0 , (A=A^) $$ совпадают с модулями корней полинома: $$ (Z)=left| begin A & B & C^/|C|\ B^ & -1 & Z-h/|C|\ C/|C| & Z-h/|C| & 0 end right| . $$ Здесь $ |C|=sqrt<c_1^2+dots+c_n^> $ и предполагается, что поверхности не пересекаются.

Пример. Найти расстояние от прямой $ 2, x_1- x_=0 $ до эллипса

$$ 7,x_1^2-4,x_1x_2 + 6, x_2^2-47, x_1 -24, x_ +124 = 0 .$$

Решение. Здесь $$ (Z)=left| begin A & B & C^/|C| \ B^ & -1 & Z-h/|C| \ C/|C| & Z-h/|C| & 0 end right| = left| begin -frac & frac & frac & frac<sqrt> \ &&& \ frac & — frac & frac &- frac<sqrt> \ &&& \ frac & frac & -1 & Z \ &&& \ frac<sqrt> & — frac<sqrt> & Z & 0 end right| = $$ $$ =-fracleft(760,Z^2+1592sqrt, Z+2383 right) $$ и корни этого полинома: $$ -fracsqrtpm frac sqrt . $$

Ответ. $$ d = left| -fracsqrt+ frac sqrt right| approx 0.809219_ . $$

Видео:Координаты середины отрезкаСкачать

Расстояние между квадриками

Теорема. Пусть $ X^ A_ X =1 $ и $ X^ A_ X =1 $ – квадрики в $ ^ $, причем первая является эллипсоидом. Квадрики не пересекаются тогда и только тогда, когда матрица $ A_-A_2 $ является знакоопределенной.

Доказательство ☞ ЗДЕСЬ.

Теорема. [3,4]. Если выполняется условие предыдущей теоремы, то квадрат расстояния между

$$ mbox X^ A_ X =1 mbox X^ A_ X =1 $$ совпадает с минимальным положительным корнем уравнения расстояний $$ (z)=0 quad npu quad (z)=_ left( Phi(lambda,z) right) . $$ Здесь $$ Phi(lambda,z)=det (lambda A_1 + (z- lambda) A_2 — lambda (z-lambda) A_1 A_2), $$ $ _ $ — дискриминант полинома рассматриваемого относительно переменной $ lambda_ $. Дополнительно предполагается, что указанный корень не является кратным.

Пример. Найти расстояние между эллипсами

$$10,x_1^2-12,x_1x_2+8,x_2^2=1 qquad u qquad x_1^2+x_1x_2+x_2^2=1 . $$

Решение. Здесь $$ A_1= left( begin 10 & — 6 \ -6 & 8 end right), quad A_2= left( begin 1 & frac \ frac & 1 end right) $$ и матрица $ A_-A_2 $ положительно определена. Следовательно эллипсы не пересекаются. $$ Phi(lambda,z)=det (lambda A_1 + (z- lambda) A_2 — lambda (z-lambda) A_1 A_2)= $$ $$ =33,lambda^4+left(-66z+fracright)lambda^3+left(33,z^2-61,z+fracright)lambda^2+left(-fracz^2+fraczright)lambda+frac,z^2 $$ и дискриминант этого полинома по переменной $ lambda_ $ равен $$ (z)=fracz^2 (, z^6-,z^5+ , z^4 -, z^3+, z^2 -,z+) . $$ Положительные корни уравнения расстояний $ (z)=0 $: $$ z_1 approx 0.053945666, z_2 approx 1.3340583883, z_3 approx 1.95921364, z_4 approx 2.8785867381 . $$

Ответ. $ d_= sqrt approx 0.23226206 $.

Нахождение координат ближайших точек на квадриках (обеспечивающих найденное расстояние) возможно по алгоритму:

1. Если $ z=z_ $ — корень полинома $ (z) $, то это значит, что полином $$ Phi(lambda, z_) = det ( lambda A_1 +(z_-lambda)A_2 — lambda (z_-lambda) A_2A_1) $$ имеет кратный корень $ lambda_ = lambda_ $. При выполнении условий теоремы, этот корень будет единственным второй кратности и его можно выразить в виде рациональной функции от $ z_ $ с помощью субдискриминантов.

2. Столбец координат $ X_^ $ точки первой квадрики, удовлетворяет тогда однородной системе уравнений $$ ( lambda_ A_1 +(z_-lambda_)A_2 — lambda_ (z_-lambda_) A_2A_1) X = mathbb O , $$ которая имеет бесконечное множество решений, поскольку определитель ее матрицы равен нулю. Из этого бесконечного множества мы выделяем те решения, что удовлетворяют условию $ X^A_X=1 $.

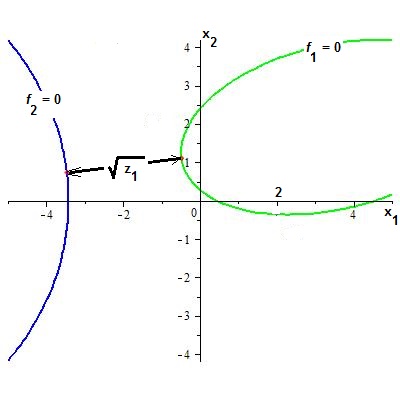
При выполнении условий теоремы таких решений будет два (что соответствует симметрии задачи, см. рисунок).

Аналогично, столбец координат $ Y_^ $ точки на второй квадрике $ Y^A_Y=1_ $ будет решением системы уравнений $$ ( lambda_ A_1 +(z_-lambda_)A_2 — lambda_ (z_-lambda_) A_1A_2) Y = mathbb O . $$

Для нахождения решений воспользуемся одним из результатов теории систем линейных уравнений. Составим столбец из алгебраических дополнений к элементам какой-либо строки матрицы $$ M= lambda_ A_1 +(z_-lambda_)A_2 — lambda_ (z_-lambda_) A_2A_1 . $$ Тогда вектор $ X_^ $ отличается от этого столбца лишь множителем, который определится из условия $ X^A_X=1_ $. Аналогично, для получения столбца координат $ Y_^ $ возьмем столбец из алгебраических дополнений к элементам какого-либо столбца той же матрицы $ M_ $ и домножим его на константу, чтобы обеспечить выполнение условия $ Y^A_Y=1_ $.

3. Получившиеся пары $ X_,Y_^ $ надо согласовать: они должны подчиняться условию $$ (X_-Y_)^(X_-Y_)=z_ . $$

Пример. Найти ближайшие точки эллипсов из предыдущего примера.

Решение. Для найденного значения $ z_=z_1 approx 0.053945666_ $ определитель матрицы $$ M=left( begin 7,lambda^2+(-7z+9)lambda+z & -2lambda^2+(2,z-frac)lambda+fracz \ & \ -lambda^2+(z-frac)lambda+fracz & 5lambda^2+(-5z+7)lambda+z end right) $$ как полином по $ lambda_ $ будет иметь кратный корень. Этот корень определяем 1) с помощью субдискриминантов в виде: $$ lambda=-frac<-725274,z^5+1455894,z^4+fracz^3-fracz^2+fracz> <17591706,z^4-109992894,z^3+fracz^2-fracz+frac> . $$ Подстановка сюда $ z=z_^ $ даст $ lambda_ approx -0.13576051_ $.

Далее, при найденных значениях $ z_ $ и $ lambda_ $ система линейных уравнений $$ MX=mathbb O_ $$ должна иметь бесконечное множество решений относительно вектора $ X_^ $. Одно из этих решений может быть построено (см. упражнение ☞ ЗДЕСЬ ) с помощью алгебраических дополнений к элементам, например, второй строки матрицы $ M_ $: $$ left( begin 2lambda^2-(2,z-frac)lambda-fracz \ \ 7,lambda^2+(-7z+9)lambda+z end right) quad begin longrightarrow \ z=z_, lambda= lambda_ end quad X=left( begin -0.8579069 \ \ -0.9876166 end right) . $$ Любое другое решение получается домножением полученного на произвольную константу («растяжением» вектора). Воспользуемся этим, чтобы добиться выполнения условия $ X^A_ X =1_ $. $$ X_=frac<sqrt<X^A_1 X>> X approx left( begin -0.3838312 \ -0.4418639 end right) . $$ Аналогично, для нахождения точки на другом эллипсе, мы решаем систему $$ M^Y=mathbb O_ , $$ представив ее решение опять-таки с помощью алгебраических дополнений к элементам второго столбца матрицы $ M_ $: $$ left( begin lambda^2-(z-frac)lambda-fracz \ \ 7,lambda^2+(-7z+9)lambda+z end right) quad begin longrightarrow \ z=z_, lambda= lambda_ end quad left( begin -0.8836615 \ \ -0.9876166 end right) quad Rightarrow quad Y_ approx left( begin -0.5449964 \ \ -0.6091105 end right) . $$

Ответ. $ pm (0.3838312,, 0.4418639)_ $ и $ pm (0.5449964,, 0.6091105)_ $ соответственно (знаки должны быть согласованы).

Проверка. Если в ответе взять знак $ +_ $: $$ X_-Y_ = left( begin -0.1611652 \ -0.1672466 end right)= lambda_ A_1X_=(lambda_-z_)A_2Y_,quad (X_-Y_)^(X_-Y_)approx mathbf4 . $$

Теорема. [3,4].Пусть

$$ X^ A_X+2,B^_1X-1=0 mbox X^ A_X+2,B^_2X-1=0 $$ — квадрики в $ ^_ $, причем первая является эллипсоидом. Квадрики пересекаются тогда и только тогда, когда среди вещественных корней полинома

$$ Theta (z) = _lambda left( det left( left[ begin A_2 & B_2\ B_2^ & -1-z end right] — lambda left[ begin A_1 & B_1\ B_1^ & -1 end right] right) right) $$ имеются числа разных знаков или нуль. Здесь $ _ $ — дискриминант полинома рассматриваемого относительно переменной $ lambda_ $.

Для того, чтобы существовала точка касания квадрик

$$ X^ A_X+2,B^_1X-1=0 mbox X^ A_X+2,B^_2X-1=0 $$ необходимо и достаточно, чтобы было выполнено условие $$ _lambda left( det left( left[ begin A_2 & B_2\ B_2^ & -1 end right] — lambda left[ begin A_1 & B_1\ B_1^ & -1 end right] right) right) =0 . $$

Теорема. [3,4]. Если не выполняется условие предыдущей теоремы, то квадрат расстояния между

$$ mbox quad X^ A_X+2,B^_1X-1=0 quad mbox quad X^ A_X+2,B^_2X-1=0 $$ совпадает с минимальным положительным корнем полинома $$ (z) = $$ $$ =_ left( det left( mu_1 left[ begin A_1 & B_1\ B_1^ & -1 end right] + mu_2 left[ begin A_2 & B_2\ B_2^ & -1 end right] — left[ begin A_2 A_1 & A_2 B_1\ B_2^ A_1 & B_2^B_1 — mu_1 mu_2 z end right] right) right), $$ в предположении, что этот корень не является кратным. Здесь $ _ $ — дискриминант полинома рассматриваемого относительно переменных $ mu_, mu_ $.

Пример. Найти расстояние между эллипсами

Ответ. $ d approx sqrt approx 3.00306481 $.

Нахождение ближайших точек на квадриках (обеспечивающих найденное расстояние) возможно по следующему алгоритму.

2. Составим матрицу $$ M= mu_ A_1+mu_A_2-A_2A_1 . $$ Тогда координатные столбцы ближайших точек на квадриках вычисляются по формулам: $$ X_=M^ (A_2B_1-mu_ B_1-mu_B_2), Y_=(M^)^<^> (A_1B_2 — mu_ B_1-mu_B_2). $$

Пример. Найти ближайшие точки эллипсов из предыдущего примера.

Ответ. $$ X_approx left(begin -0.4824707833 \ 1.1065143947 end right), Y_approx left( begin -3.46262940675\ 0.73630788509 end right) . $$

Проверка. $$ (X_-Y_)^(X_-Y_)approx mathbf3 , $$ $$ X_^A_1X_+2B_1^X_-1 approx 1cdot 10^ , Y_^A_2Y_+2B_2^Y_-1approx -3cdot 10^ , $$ и вектор $ X_-Y_^ $ перпендикулярен обоим эллипсам в соответствующих ближайших точках: $$ A_1X_+B_1= left(begin 1.767863990 \ 0.219610712 end right)=mu_ (X_-Y_), A_2Y_+B_2= left(begin -0.1254448880 \ -0.0155832356 end right)=-mu_ (X_-Y_) . $$

Пример. Найти расстояние между эллипсоидами

$$ 7,x_1^2+6,x_2^2+5,x_3^2-4,x_1x_2-4,x_2x_3-37,x_1-12,x_2+3,x_3+54=0$$ и $$ 189,x_1^2+x_2^2+189,x_3^2+2,x_1x_3-x_2x_3-27=0 .$$

Ответ. $ d approx sqrt approx 1.1635198754_ $

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Алгебраические кривые и многообразия

Видео:Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Расстояние от точки до плоской алгебраической кривой

Задача. Пусть алгебраическая кривая задана уравнением $$ Phi(x,y)=0 . $$ Здесь $ Phi_(x,y) $ — отличный от константы полином от $ x_ $ и $ y_ $ с вещественными коэффициентами. Требуется найти расстояние до этой кривой от начала координат.

Здесь возникает проблема, которую для рассмотренных выше случаев удавалось либо обойти, либо же сравнительно дешево решить: это проблема существования решения. Дело в том, что уравнение может не иметь вещественных решений, то есть не определять никакой кривой на плоскости $ mathbb R^ $.

Будем решать задачу сначала для частного случая — пусть полином $ Phi_(x,y) $ является четным по переменной $ y_ $. Геометрически это означает, что кривая (если она существует) будет зеркально симметричной относительно оси $ mathbb Ox $. А с аналитической точки зрения такой полином можно представить в виде полинома $$ F(x,Y) equiv Phi_(x,y) quad npu quad Y=y^2 . $$

Теорема 1 [6]. Пусть $ Phi_(x,y) equiv Phi_(x,-y) $. Уравнение $ Phi_(x,y)=0 $ не имеет вещественных решений если одновременно выполняются два условия:

a) уравнение $ Phi(x,0)=0 $ не имеет вещественных решений;

б) уравнение $$ mathcal F(z)=mathcal D_x( F(x,z-x^2))=0 $$ не имеет положительных решений.

Если хотя бы одно из этих условий не выполняется, то квадрат расстояния от начала координат до кривой $ Phi(x_,y)=0 $ равен либо квадрату минимального по модулю вещественного корня уравнения $ Phi(x,0)=0 $, либо же минимальному положительному корню уравнения $ mathcal F(z)= 0 $, при условии, что последний не является кратным. Здесь $ _ $ — дискриминант полинома, рассматриваемого относительно переменной $ x_ $.

Пример. Найти расстояние от начала координат до кривой

Решение. Уравнение $$ Phi(x,0)=x^6-6,x^5+25,x-45=0 $$ имеет вещественные корни $ mu_1approx -1.621919 $ и $ mu_2 approx 5.986387 $. 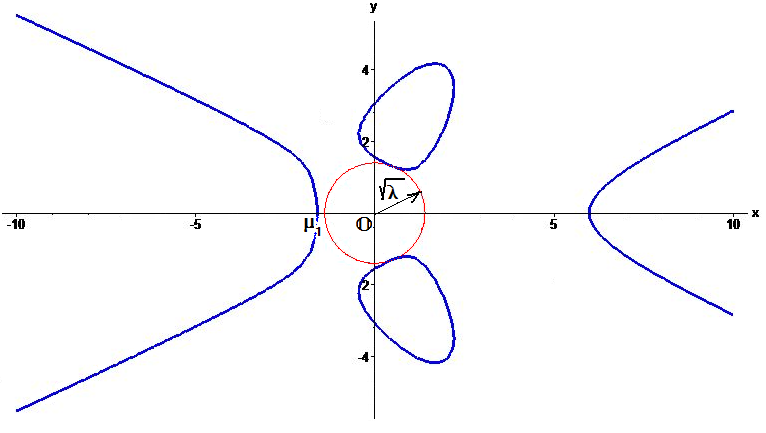Далее, $$ F(x,Y)=x^6-5,x^4Y-Y^3-6,x^5+6,xY^2+10,Y^2+25,x-45 $$ и полином $$ mathcal F(z)=mathcal D_x (F(x,z-x^2))= ,z^-z^-,z^+,z^+ z^ $$ $$ -z^+ ,z^9+,z^8-,z^7+,z^6+ $$ $$ +z^5 -,z^4+,z^3+,z^2-, z+ $$ $$ + $$ имеет минимальный положительный корень равный $ lambda approx 1.965293 $. Поскольку $ sqrt 4) , задача о трёх заводах.

Пример. В точках $ P_,P_2,P_3 $ расположены источники полезных ископаемых: железной руды, угля и воды соответственно. Известно, что для производства одной тонны стали необходимо иметь $ m_ $ тонн руды, $ m_2 $ тонн угля и $ m_3 $ тонн воды. В предположении, что стоимость перевозки одной тонны груза не зависит от его природы, где следует расположить сталелитейное производство так, чтобы минимизировать транспортные издержки?

Подробное обсуждение этой задачи (и к ней примыкающих) ☞ ЗДЕСЬ.

Задача о точке Лемуана-Греба

Задача. Найти точку плоскости, cумма квадратов расстояний от которой до сторон треугольника, лежащего в этой же плоскости, минимальна.

Решение. Пусть $ d_1, d_2,d_3 $ — расстояния от точки $ P_ $ плоскости до сторон треугольника с длинами $ D_1, D_2, D_3 $ соответственно. Воспользуемся тождеством Лагранжа: $$ (d_1^2+ d_2^2+d_3^2)(D_1^2+ D_2^2+D_3^2)equiv $$ $$ equiv (d_1D_1+ d_2D_2+d_3D_3)^2+(d_1D_2-d_2D_1)^2+(d_2D_3-d_3D_2)^2+ (d_1D_3-d_3D_1)^2 . $$ Величина $ d_1D_1+ d_2D_2+d_3D_3 $ является постоянной, не зависящей от координат точки $ P_ $: $$ d_1D_1+ d_2D_2+d_3D_3 =2S , $$ где $ S_ $ — площадь данного треугольника. Следовательно $ min (d_1^2+d_2^2+d_3^2) $ достигается при условиях $$ d_1D_2-d_2D_1=0, d_2D_3-d_3D_2=0, d_1D_3-d_3D_1=0 , $$ то есть когда $$ frac=frac=frac . $$ Определяемая этими соотношениями точка называется точкой Лемуана 6) или точкой Греба 7) ; в ней пересекаются симедианы треугольника.

Еще некоторые задачи

Построение прямой на плоскости, сумма квадратов расстояний до которой от заданных точек минимальна ☞ ЗДЕСЬ

Видео:Координаты точки и координаты вектора 1.Скачать

§3.2 Перпендикуляр из точки на под пространство. Кратчайшее расстояние от точки до подпространства*).

Видео:Расстояние от точки до плоскости / Вывод формулыСкачать

Primary tabs

Forums:

Определение 2. Пусть $ R_1 -$ подпространство евклидова пространства R. Мы будем говорить, что вектор $ h in R$ ортогонален подпространству $ R_1$, если он ортогонален любому вектору x из $ R_1$.

Если вектор h ортогонален векторам $ e_1, e_2, . e_m, $ то он ортогонален любой их линейной комбинации. Действительно из равенств
$$ (h, e_i) = 0 $$
следует, что для любых чисел $ lambda_1, lambda_2, . lambda_m $
$$ (h_1, lambda_1 e_1 + lambda_2 e_2 + . + lambda_m e_m) = 0. $$
Поэтому, для того чтобы вектор h был ортогонален m-мерному подпространству $ R_1$, достаточно, чтобы он был ортогонален m линейно независимым векторам из $ R_1$ (базису в $ R_1$ **).

Упражнение. Показать, что совокупность всех векторов $ y in R,$ ортогональных к подпространству $ R_1,$ также образует подпространство пространства R. Это подпространство называется ортогональным дополнением к подпространству $ R_1$ в пространстве R.

Рассмотрим в пространстве R некоторое m-мерное подпространство $R_1$ ***) и вектор f, не принадлежащий $ R_1$. Поставим задачу: опустить перпендикуляр из точки f на $ R_1$, т. е. найти вектор $f_0$ из $R_1$ такой, чтобы вектор $ h = f — f_0$ был ортогонален $ R_1$. Вектор $f_0$ называется при этом ортогональной проекцией вектора f на подпространство $R_1$. Несколько позже мы увидим, что эта задача имеет решение, притом единственное. Сейчас мы покажем, что, как и в элементарной геометрии, перпендикуляр есть кратчайшее расстояние от точки до подпространства. Другими словами, покажем, что если $f_1$ есть отличный от $ f_0$ вектор из $ R_1,$ то
$$ |f-f_1| > |f-f_0|. $$

Действительно, вектор $ f_0 — f_1,$ как разность двух векторов из $ R_1$, принадлежит $ R_1$, и, следовательно, ортогонален вектору $ h = f — f_0.$ По теореме Пифагора имеем:
$$ |f — f_0|^2 + |f_0 — f_1|^2 = |f — f_0 + f_0 — f_1|^2 = |f — f_1|^2 $$
и, значит,
$$ | f — f_1| > |f — f_0|. $$

Покажем теперь, как фактически вычислить по f его ортогональные проекцию $ f_0$ на подпространство $ R_1$ (т. е. опустить перпендикуляр из f на $ R_1$). Пусть базис подпространства $ R_1$ состоит из векторов $ e_1, e_2, . e_m.$ Будем искать вектор $ f_0$ в виде
$$ f_0 = c_1 e_1 + c_2 e_2 + . + c_m e_m, qquad qquad (9)$$
где коэффициенты $c_k$ найдем из условия ортогональности $ f — f_0 $ к $ R_1.$ Для того чтобы эта ортогональность имела место, необходимо и достаточно, чтобы выполнялись m равенств $ (f — f_0, e_k) = 0 (k = 1, 2, . m), $ т. е.
$$ ( f_0, e_k) = (f, e_k). qquad qquad (10) $$
Подставляя сюда вместо $f_0$ его выражение (9), получаем систему m уравнений
$$ c_1 (e_1, e_k) + c_2 (e_2, e_k) + . + c_m (e_m, e_k) = (f, e_k)$$
$$ (k = 1, 2, . m) qquad qquad (11)$$
относительно чисел $ c_i$.

Рассмотрим сначала отдельно часто встречающийся случай, когда базис $ e_1, e_2, . e_m -$ ортогональный и нормированный. В этом случае задача решается особенно просто. Действительно система (11) превращается в таком базисе в систему равенств
$$ c_i = (f, e_i), qquad qquad (12) $$
сразу определяющих нудные коэффициенты.

Так как в каждом m-серном подпространстве можно выбрать Ортогональный нормированный базис, то мы доказали, таким образом, что у каждого вектора f существует, и притом только одна, ортогональная проекция $ f_0$ на подпространство $ R_1. $

Вернёмся теперь к случаю произвольного базиса. В этом случае система 11) также должна иметь единственное решение. Действительно, вектор $f_0$, по дрказанному, существует и притом только один. В базисе $ e_1, e_2, . e_m. $ вектор $ f_0$ имеет вполне определенные координаты $ c_1, c_2, . c_m.$ Так как эти числа удовлетворяют системе (11), то эта система имеет, следовательно, единственное решение. Система m уравнений с m неизвестными может иметь единственное решение, лишь если не определитель отличен от нуля. Отсюда следует, что определитель системы (11)
$$begin
(e_1, e_1) & (e_2, e_1) & cdots & (e_m, e_1) \
(e_1, e_2) & (e_2, e_2) & cdots & (e_m, e_2) \
cdots & cdots & cdots & cdots \
(e_1, e_m) & (e_2, e_m) & cdots & (e_m, e_m)\
end$$
отличен от нуля. Этот определитель называется определителем Грама векторов $ e_1, e_2, . e_m.$

Итак, пусть задано подпространство $R_1$ с базисом $ e_1, . e_m $ и произвольный вектор f пространства R. Ортогональная проекция $ f_0$ вектора f на $ R_1$ имеет вид
$$ f_0 = c_1 e_1 + . + c_m e_m. $$
При этом, если базис $ e_1, e_2, . e_m $ ортогонален, то
$$ c_i = (f, e_i).$$
Если же базис $ e_1, . e_m $ произволен, то коэффициенты $ c_i$ определяются как решение системы (11).

Пример 1. Способ наименьших квадратов. Предположим, что величина y есть линейная функция величин $ x_1, . x_m, $ т. е. что
$$ y = c_1 x_1 + . + c_m x_m, $$
где $ c_1, . c_m — $ постоянные, неизвестные нам коэффициенты. Часто коэффициенты $ c_1, . c_m $ определяются экспериментально. Для этого производится ряд измерений величин $ x_1, . x_m$ и y. Обозначим результаты k-го измерения через $ x_, . x_$ и, соответственно, $y_k.$
Коэффициенты $ c_1, . c_m $ можно было бы попытаться определить из системы уравнений
$$
left.begin
x_ c_1 + x_ c_2 + . + x_ c_m = y_1, \
x_ c_1 + x_ c_2 + . + x_ c_m = y_2, \
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . \
x_ c_1 + x_ c_2 + . + x_ c_m = y_n.
endrightrbrace qquad qquad (13)
$$
Здесь число уравнений n равно числу произведенных измерений и обычно превосходит число неизвестных $ (n>m). $ Так как измерение величин $ x_1, . x_n, y$ неизбежно связано с погрешностями, то система (13), вообще говоря, противоречива и о ее точно решении говорит бессмысленно. Поэтому уравнениям (13) можно удовлетворить лишь приближенно. Таким образом, ставится задача разыскать такие значения неизвестных $ c_1, . c_m, $ при которых левые части уравнения (13) были бы возможно более близки к соответствующим правым частям. В качестве «меры близости» берется так называемое левых частей уравнений от свободных членов, т. е. величина
$$ sum_^n (x_ c_1 + x_ c_2 + . + x_ c_m — y_k)^2. qquad qquad (14) $$
Нам нужно найти числа $ c_1, c_2, . c_m, $ при которых квадратичное уклонение имеет наименьшее значение.Эту задачу на минимум можно решить непосредственно. Однако ее решение можно сразу получить из результатов, изложенных выше.

В самом деле, рассмотрим n-мерное евклидово пространство и векторы $ e_1 = (x_, x_, . x_), e_2 = (_, . x_, . $
$ . e_m = (_, . x_)$ и $ f=(y_1, . y_n) $ в этом пространстве. Правые части уравнений системы (13) являются компонентами вектора f, левые части — вектора
$$ c_1 e_1 + c_2 e_2 + . + c_m e_m. $$
Выражение (14) есть, следовательно, квадрат расстояния вектора $ c_1 e_1 + c_2 e_2 + . + c_m e_m $ от вектора f. Таким образом, условие, чтобы квадратичное уклонение было минимальным, равносильно следующей задаче: выбрать числа $ c_1, c_2, . c_m $ так, чтобы расстояние вектора f до вектора $ I_0 = c_1 e_1 + c_2 e_2 + . + c_m e_m $ было наименьшим. Если обозначить через $ R_1$ подпространство n-мерного пространства, состоящее из линейных комбинаций векторов $ e_1, e_2, . e_m *), $ то задача состоит в нахождении проекции вектора f на это подпространство. Как мы видели (формула (11)), числа $ c_1, c_2, . c_m, $ решающие эту задачу, находятся из системы уравнений
$$
left.begin
(e_1, e_1) c_1 + (e_2, e_1) c_2 + . + (e_m, e_1) c_m = (f, e_1), \
(e_1, e_2) c_1 + (e_2, e_2) c_2 + . + (e_m, e_2) c_m = (f, e_2), \
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . \
(e_1, e_m) c_1 + (e_2, e_m) c_2 + . +(e_m, e_m) c_m = (f, e_m),
endrightrbrace
$$
где
$$ (f, e_k) = sum_^n x_ y_j; (e_i, e_k) = sum_^n x_ x_. $$

Система (15) называется в этом случае системой нормальных уравнений . Итак, приближенное решение системы (13) состоит в замене ее нормальной системой (15) m уравнений с m неизвестными. Изложенный метод называется способом наименьших квадратов.

Упражнение. Решить по способу наименьших квадратов систему уравнений
$$ 2c = 3,
3c = 4,
4c = 5. $$
Решение. $ e_1 = (2, 3, 4), f = (3, 4, 5). $ Нормальная система сводится в этом случае к одному уравнению:
$$ (e_1, e_1) c=(e_1, f_1),$$
т. е.
$$ 29c = 40; c = <over >. $$

Для случая, когда система (13) есть система n уравнений с одним неизвестным
$$ x_1 c = y_1,
x_2 c = y_2,
. . . . . . . . . . . qquad qquad (13′)
x_n c = y_n, $$
решение запишется следующим образом:
$$ c= <over > = << sum_^n> x_k y_k over < sum_^n x_k^2>> $$
Приближенное решение системы (13′) может быть истолковано геометрически как проведение через начало координат прямой, проходящий «возможно более близко» от совокупности точек $ (x_1, y_1), (x_2, y_2), . (x_n, y_n).$ Число c представляет тогда угловой коэффициент такой прямой.

Пример 2. Приближение функций тригонометрическими многочленами. Пусть $ f(t) -$ некоторая непрерывная функция, заданная на интервале $ (0, 2π)$. Часто бывает нужно подобрать тригонометрический многочлен. $ P(t)$ данного порядка, возможно меньше отличающийся от $ f(t).$ В качестве меры отклонения $ P(t) $ от $ f_(t) $ мы возьмём квадратичное уклонение, которое задаётся формулой
$$ intlimits_0^ [f(t) — P(t)]^2 dt. qquad qquad (16)$$

Итак, точная постановка рассматриваемой задачи такова: среди всех тригонометрических многочленов порядка n
$$ P(t) = << alpha_0 over > + alpha_1 cos t+b_1 sin t + . + alpha_n cos nt + b_n sin nt qquad qquad (17)
найти тот, квадратичное уклоне которого от ваданной функции $ f(t) $ минимально.

Введем в рассмотрение пространство R непрерывных функций на отрезке $ (0; 2π).$ Скалярное произведение в этом пространстве зададим, как обычно, интегралом
$$ (g, g) = intlimits_0^2π f(t) g(t) dt.$$
Длина вектора выражается тогда формулой
$$ |f| = sqrt, $$
и следовательно, квадратичное уклонение (16) есть в нашем пространстве просто квадрат расстояния от $ i(t) $ до $P(t).$ Тригонометрические многочлены вида (17) образуют в R подпространство $ R_1$ размерности $ 2π + 1$. Нам нужно найти элемент из $ R_1,$ находящийся на минимальном расстоянии от $ f(t). $ Эта задача снова решается опусканием перпендикуляра из точки $ f(t) $ на подпространство $R_1$.
Так функции
$$ e_0 = <over < sqrt>>; e_1 = <over < sqrt>>; e_2 = <over < sqrt>>; . ; e_ = <over < sqrt>>; e_ = <over < sqrt>>; $$
образуют ортогональный и нормированный базис в этом подпространстве (см. пример 2 предыдущего пункта), то решением этой задачи служит линейная комбинация базисных векторов.
$$ P(t) = sum_^ c_k e_k, qquad qquad (18)$$
где
$$ c_k = (f, e_k), $$
т. е., вспоминая определение скалярного произведения имееим:
$$ c_0 = <over < sqrt>> intlimits_0^ f(t) dt; c_ = <over < sqrt>> intlimits_0^ f(t) cos kt dt; $$
$$ c_ = <over > intlimits_0^ f(t) sin kt dt qquad (k=1, . n). $$
Подставляя $ c_k $ и $e_k (k=1, . n)$ в формулу (18), мы приходим, таким образом, к следующему результату: для того чтобы определить тригонометрический многочлен
$$ P(t) = <over > + sum_^n alpha_k cos kt + b_k sin kt, $$
квадратичное уклонение которого от заданной функции $ f(t) $ минимально, надо определить коэффициенты $ alpha_k, b_k$ по формулам
$$ alpha_0 = <over > intlimits_0^ f(t) dt; alpha_k = <over > intlimits_0^ f(t) kt dt; b_k = <over > intlimits_0^ f(t) sin kt dt. $$
Так определенные числа $ alpha_k, b_k$ называются коэффициентами Фурье функции f(t).

🎥 Видео

Уравнения прямой на плоскости | Векторная алгебраСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Расстояние от точки до плоскости. 11 класс.Скачать

Найдите разложение вектора по векторам (базису)Скачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Расстояние от точки до прямой (метод координат)Скачать