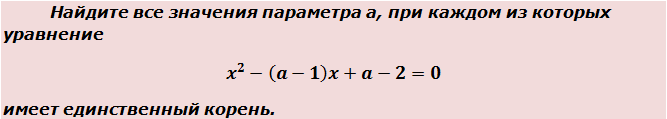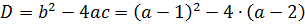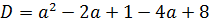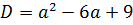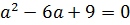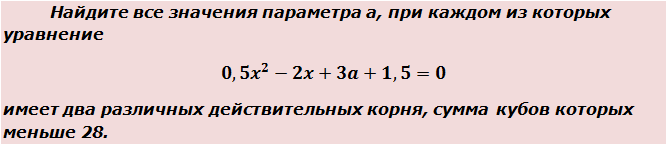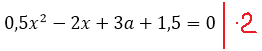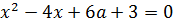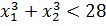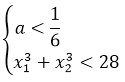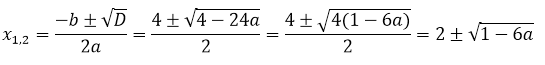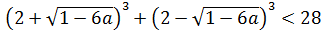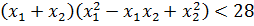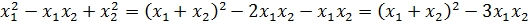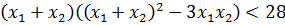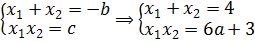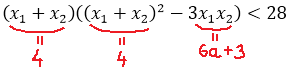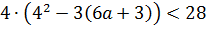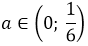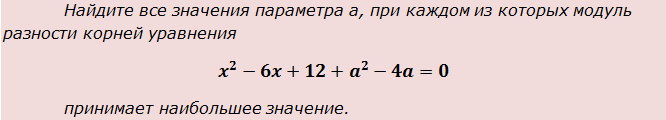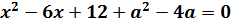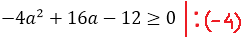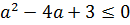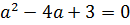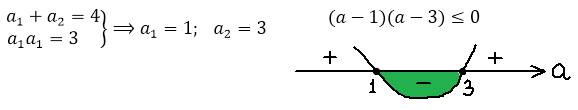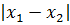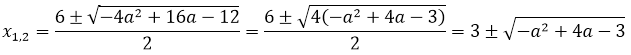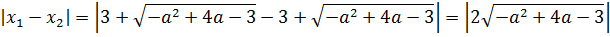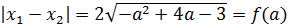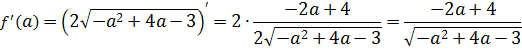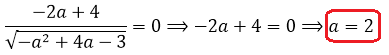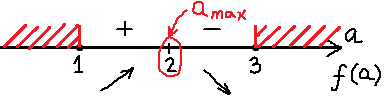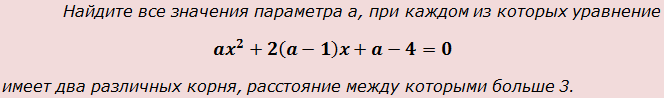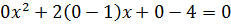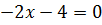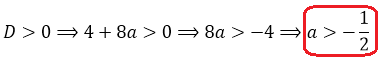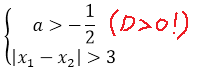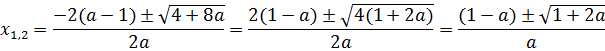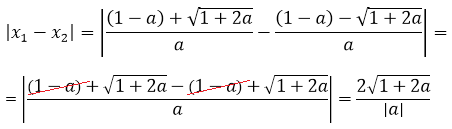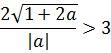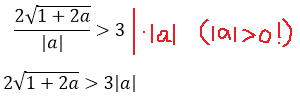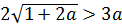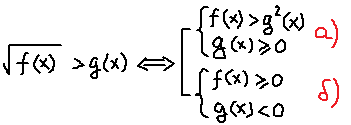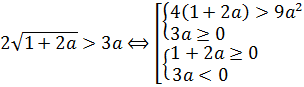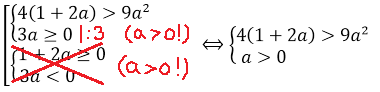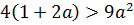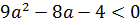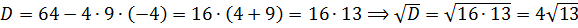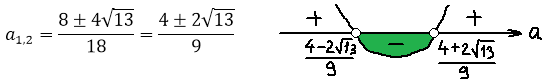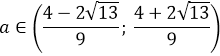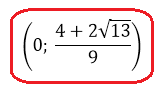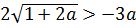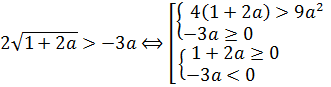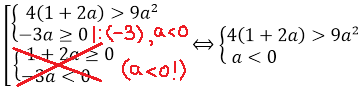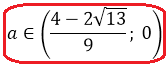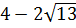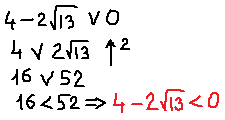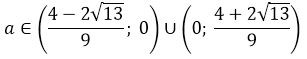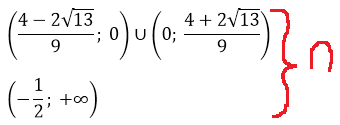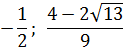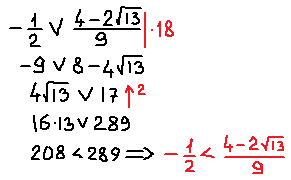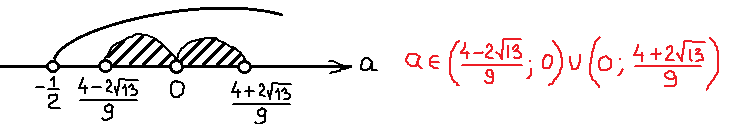Как найти расстояние между корнями квадратного уравнения (4 видео)

Квадратные уравнения с параметром

Задачи с параметрами. Простейшие задачи на квадратный трёхчлен.

Сегодня мы рассмотрим задачи на квадратный трёхчлен, про который, в зависимости от параметра, надо будет что-то выяснить. Это «что-то» может быть самым разнообразным, насколько только хватит фантазии у составителей задачи. Это самый простой тип задач с параметрами. И, если на ЕГЭ вам попалась такая — считайте, что вам повезло!

Но, прежде чем приступать к разбору самих задач, ответьте сами себе на такие простые вопросы:

— Что такое квадратное уравнение, как оно выглядит и как решается?

— Что такое дискриминант и куда его пристроить?

— Что такое теорема Виета и где её можно применить?

Если вы верно отвечаете на эти простые вопросы, то 50% успеха в решении параметрических задач на квадратный трёхчлен вам обеспечены! А остальные 50% — это обычная алгебра и арифметика: раскрытие скобок, приведение подобных, решение уравнений, неравенств и систем и т.д.

Для начала рассмотрим совсем безобидную задачку. Для разминки. 🙂

Пример 1

Приступаем к решению. Во-первых, чтобы в будущем не накосячить в коэффициентах, всегда полезно выписать их отдельно. Прямо в столбик. Вот так:

Да-да! Часть коэффициентов в уравнении (а именно — b и с) зависит от параметра. В этом как раз и состоит вся фишка таких задач. А теперь снова въедливо перечитываем условие. Ключевой зацепкой в формулировке задания являются слова «единственный корень». И когда же квадратное уравнение имеет единственный корень? Подключаем наши теоретические знания о квадратных уравнениях. Только в одном единственном случае — когда его дискриминант равен нулю.

Осталось составить выражение для дискриминанта и приравнять его к нулю. Поехали!

Теперь надо приравнять наш дискриминант к нулю:

Можно, конечно, решать это квадратное уравнение через дискриминант, а можно немного схитрить. На что у нас похожа левая часть, если как следует присмотреться? Она у нас похожа на квадрат разности (a-3) 2 !

Респект внимательным! Верно! Если заменить наше выражение слева на (a-3) 2 , то уравнение будет решаться в уме!

Вот и всё. Это значит, что единственный корень наше квадратное уравнение с параметром будет иметь только в одном единственном случае — когда значение параметра «а» равно тройке.)

Это был разминочный пример. Чтобы общую идею уловить.) Теперь будет задачка посерьёзнее.

Пример 2

Вот такая задачка. Начинаем распутывать. Первым делом выпишем наше квадратное уравнение:

0,5x 2 — 2x + 3a + 1,5 = 0

Самым логичным шагом, было бы умножить обе части на 2. Тогда у нас исчезнут дробные коэффициенты и само уравнение станет посимпатичнее. Умножаем:

Выписываем в столбик наши коэффициенты a, b, c:

Видно, что коэффициенты a и b у нас постоянны, а вот свободный член с зависит от параметра «а»! Который может быть каким угодно — положительным, отрицательным, целым, дробным, иррациональным — всяким!

А теперь, чтобы продвинуться дальше, вновь подключаем наши теоретические познания в области квадратных уравнений и начинаем рассуждать. Примерно так:

«Для того чтобы сумма кубов корней была меньше 28, эти самые корни, во-первых, должны существовать. Сами по себе. В принципе. А корни у квадратного уравнения существуют, тогда и только тогда, когда его дискриминант неотрицательный. Кроме того, в задании говорится о двух различных корнях. Эта фраза означает, что наш дискриминант обязан быть не просто неотрицательным, а строго положительным!»

Если вы рассуждаете таким образом, то вы движетесь правильным курсом! Верно.) Составляем условие положительности для дискриминанта:

Полученное условие говорит нам о том, что два различных корня у нашего уравнения будет не при любых значениях параметра «а», а только при тех, которые меньше одной шестой! Это глобальное требование, которое должно выполняться железно. Неважно, меньше 28 наша сумма кубов корней или больше. Значения параметра «а», большие или равные 1/6, нас заведомо не устроят. Гуд.) Соломки подстелили. Движемся дальше.

Теперь приступаем к загадочной сумме кубов корней. По условию она у нас должна быть меньше 28. Так и пишем:

Значит, для того чтобы ответить на вопрос задачи, нам надо совместно рассмотреть два условия:

А дальше начинаем отдельно работать с этой самой суммой кубов. Есть два способа такой работы: первый способ для трудолюбивых и второй способ — для внимательных.

Способ для трудолюбивых заключается в непосредственном нахождении корней уравнения через параметр. Прямо по общей формуле корней. Вот так:

Теперь составляем нужную нам сумму кубов найденных корней и требуем, чтобы она была меньше 28:

А дальше — обычная алгебра: раскрываем сумму кубов по формуле сокращённого умножения, приводим подобные, сокращаем и т.д. Если бы корни нашего уравнения получились покрасивее, без радикалов, то такой «лобовой» способ был бы неплох. Но проблема в том, что наши корни выглядят немного страшновато. И подставлять их в сумму кубов как-то неохота, да. Поэтому, для того чтобы избежать этой громоздкой процедуры, я предлагаю второй способ — для внимательных.

Для этого раскрываем сумму кубов корней по соответствующей формуле сокращенного умножения. Прямо в общем виде:

А дальше проделываем вот такой красивый фокус: во вторых скобках выражаем сумму квадратов корней через сумму корней и их произведение. Вот так:

Казалось бы, и что из этого? Сейчас интересно будет! Давайте, посмотрим ещё разок на наше уравнение. Как можно внимательнее:

Чему здесь равен коэффициент при x 2 ? Правильно, единичке! А как такое уравнение называется? Правильно, приведённое! А, раз приведённое, то, стало быть, для него справедлива теорема Виета:

Вот и ещё одна теорема нам пригодилась! Теперь, прямо по теореме Виета, подставляем сумму и произведение корней в наше требование для суммы кубов:

Осталось раскрыть скобки и решить простенькое линейное неравенство:

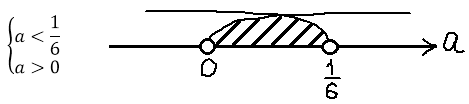
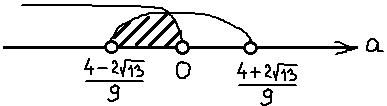
Вспоминаем, что ещё у нас есть глобальное требование a 0 необходимо пересечь с условием a . Рисуем картинку, пересекаем, и записываем окончательный ответ.

Да. Вот такой маленький интервальчик. От нуля до одной шестой… Видите, насколько знание теоремы Виета, порой, облегчает жизнь!

Вот вам небольшой практический совет: если в задании говорится о таких конструкциях, как сумма, произведение, сумма квадратов, сумма кубов корней, то пробуем применить теорему Виета. В 99% случаев решение значительно упрощается.

Это были довольно простые примеры. Чтобы суть уловить. Теперь будут примеры посолиднее.

Например, такая задачка из реального варианта ЕГЭ:

Пример 3

Что, внушает? Ничего не боимся и действуем по нашему излюбленному принципу: «Не знаешь, что нужно, делай что можно!»

Опять аккуратно выписываем все коэффициенты нашего квадратного уравнения:

А теперь вчитываемся в условие задачи и находим слова «модуль разности корней уравнения». Модуль разности нас пока не волнует, а вот слова «корней уравнения» примем во внимание. Раз говорится о корнях (неважно, двух одинаковых или двух различных), то наш дискриминант обязан быть неотрицательным! Так и пишем:

Что ж, аккуратно расписываем наш дискриминант через параметр а:

А теперь решаем квадратное неравенство. По стандартной схеме, через соответствующее квадратное уравнение и схематичный рисунок параболы:

Значит, для того чтобы у нашего уравнения в принципе имелись хоть какие-то корни, параметр а должен находиться в отрезке [-1; 3]. Это железное требование. Хорошо. Запомним.)

А теперь приступаем к этому самому модулю разности корней уравнения. От нас хотят, чтобы вот такая штука

принимала бы наибольшее значение. Для этого, ничего не поделать, но теперь нам всё-таки придётся находить сами корни и составлять их разность: x₁ — x₂. Теорема Виета здесь в этот раз бессильна.

Что ж, считаем корни по общей формуле:

Дальше составляем модуль разности этих самых корней:

Теперь вспоминаем, что корень квадратный — величина заведомо неотрицательная. Стало быть, без ущерба для здоровья, модуль можно смело опустить. Итого наш модуль разности корней выглядит так:

И эта функция f(a) должна принимать наибольшее значение. А для поиска наибольшего значения у нас есть такой мощный инструмент, как производная! Вперёд и с песнями!)

Дифференцируем нашу функцию и приравниваем производную к нулю:

Получили единственную критическую точку a = 2. Но это ещё не ответ, так как нам ещё надо проверить, что найденная точка и в самом деле является точкой максимума! Для этого исследуем знаки нашей производной слева и справа от двойки. Это легко делается простой подстановкой (например, а = 1,5 и а = 2,5).

Слева от двойки производная положительна, а справа от двойки — отрицательна. Это значит, что наша точка a = 2 и вправду является точкой максимума. Заштрихованная зона на картинке означает, что нашу функцию мы рассматриваем только на отрезке [1; 3]. Вне этого отрезка нашей функции f(a) попросту не существует. Потому, что в заштрихованной области наш дискриминант отрицательный, и разговоры о каких-либо корнях (и о функции тоже) бессмысленны. Это понятно, думаю.

Всё. Вот теперь наша задача полностью решена.

Здесь было применение производной. А бывают и такие задачи, где приходится решать уравнения либо неравенства с так ненавистными многими учениками модулями и сравнивать некрасивые иррациональные числа с корнями. Главное — не бояться! Разберём похожую злую задачку (тоже из ЕГЭ, кстати).

Пример 4

Итак, приступаем. Первым делом замечаем, что параметр а ни в коем случае не может быть равен нулю. Почему? А вы подставьте в исходное уравнение вместо а нолик. Что получится?

Получили линейное уравнение, имеющее единственный корень x=2. А это уже совсем не наш случай. От нас хотят, чтобы уравнение имело два различных корня, а для этого нам необходимо, чтобы оно, как минимум, было хотя бы квадратным.)

При всех остальных значениях параметра наше уравнение будет вполне себе квадратным. И, следовательно, чтобы оно имело два различных корня, необходимо (и достаточно), чтобы его дискриминант был положительным. То есть, первое наше требование будет D > 0.

А далее по накатанной колее. Считаем дискриминант:

D = 4(a-1) 2 — 4a(a-4) = 4a 2 -8a+4-4a 2 +16a = 4+8a

Вот так. Значит, наше уравнение имеет два различных корня тогда и только тогда, когда параметр a > -1/2. При прочих «а» у уравнения будет либо один корень, либо вообще ни одного. Берём на заметку это условие и движемся дальше.

Далее в задаче идёт речь о расстоянии между корнями. Расстояние между корнями, в математическом смысле, означает вот такую величину:

Зачем здесь нужен модуль? А затем, что любое расстояние (что в природе, что в математике) — величина неотрицательная. Причём здесь совершенно неважно, какой именно корень будет стоять в этой разности первым, а какой вторым: модуль — функция чётная и сжигает минус. Точно так же, как и квадрат.

Значит, ответом на вопрос задачи является решение вот такой системы:

Теперь, ясен перец, нам надо найти сами корни. Здесь тоже всё очевидно и прозрачно. Аккуратно подставляем все коэффициенты в нашу общую формулу корней и считаем:

Отлично. Корни получены. Теперь начинаем формировать наше расстояние:

Наше расстояние между корнями должно быть больше трёх, поэтому теперь нам надо решить вот такое неравенство:

Неравенство — не подарок: модуль, корень… Но и мы всё-таки уже решаем серьёзную задачу №18 из ЕГЭ! Делаем всё что можно, чтобы максимально упростить внешний вид неравенства. Мне здесь больше всего не нравится дробь. Поэтому первым делом я избавлюсь от знаменателя, умножив обе части неравенства на |a|. Это можно сделать, поскольку мы, во-первых, в самом начале решения примера договорились, что а ≠ 0, а во-вторых, сам модуль — величина неотрицательная.

Итак, смело умножаем обе части неравенства на положительное число |a|. Знак неравенства сохраняется:

Вот так. Теперь в нашем распоряжении имеется иррациональное неравенство с модулем. Ясное дело, для того чтобы решить его, надо избавляться от модуля. Поэтому придётся разбивать решение на два случая — когда параметр а, стоящий под модулем, положителен и когда отрицателен. Другого пути избавиться от модуля у нас, к сожалению, нет.

Случай 1 (a>0, |a|=a)

В этом случае наш модуль раскрывается с плюсом, и неравенство (уже без модуля!) принимает следующий вид:

Неравенство имеет структуру: «корень больше функции». Такие иррациональные неравенства решаются по следующей стандартной схеме:

Отдельно рассматривается случай а), когда обе части неравенства возводятся в квадрат и правая часть неотрицательна и отдельно — случай б), когда правая часть всё-таки отрицательна, но зато сам корень при этом извлекается.) И решения этих двух систем объединяются.

Тогда, в соответствии с этой схемой, наше неравенство распишется вот так:

А теперь можно существенно упростить себе дальнейшую работу. Для этого вспомним, что в случае 1 мы рассматриваем только a>0. С учётом этого требования, вторую систему можно вообще вычеркнуть из рассмотрения, поскольку, второе неравенство в ней (3a 0 и a

Упрощаем нашу совокупность с учётом главного условия a>0:

Вот так. А теперь решаем самое обычное квадратное неравенство:

Нас интересует промежуток между корнями. Стало быть,

Отлично. Теперь этот промежуток пересекаем со вторым условием системы a>0:

Есть. Таким образом, первым кусочком ответа к нашему неравенству (а пока не ко всей задаче!) будет вот такой интервал:

Всё. Случай 1 разложен по полочкам. Переходим к случаю 2.

Случай 2 (a

В этом случае наш модуль раскрывается с минусом, и неравенство принимает следующий вид:

Опять имеем структуру: «корень больше функции». Применяем нашу стандартную схему с двумя системами (см. выше):

С учётом общего требования a

А дальше снова решаем обычное квадратное неравенство:

И опять сокращаем себе работу. Ибо оно у нас уже решено в процессе разбора случая 1! Решение этого неравенства выглядело вот так:

Осталось лишь пересечь этот интервал с нашим новым условием a

Вот и второй кусочек ответа готов:

Кстати сказать, как я узнал, что ноль лежит именно между нашими иррациональными корнями? Легко! Очевидно, что правый корень заведомо положителен. А что касается левого корня, то я просто в уме сравнил иррациональное число

с нулём. Вот так:

А теперь объединяем оба найденных интервала. Ибо мы решаем совокупность (а не систему):

Готово дело. Эти два интервала — это пока ещё только решение неравенства

Кто забыл, данное неравенство отвечает у нас за расстояние между корнями нашего уравнения. Которое должно больше 3. Но! Это ещё не ответ!

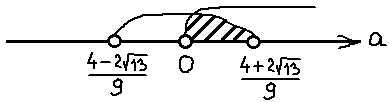
Ещё у нас есть условие положительного дискриминанта! Неравенство a>-1/2, помните? Это значит, что данное множество нам ещё надо пересечь с условием a>-1/2. Иными словами, теперь мы должны пересечь два множества:

Но есть одна проблемка. Мы не знаем, как именно расположено на прямой число -1/2 относительно левого (отрицательного) корня. Для этого нам придётся сравнить между собой два числа:

Поэтому сейчас берём черновик и начинаем сравнивать наши числа. Примерно так:

Это значит, что дробь -1/2 на числовой прямой находится левее нашего левого корня. И картинка к окончательному ответу задачи будет какая-то вот такая:

Всё, задача полностью решена и можно записывать окончательный ответ.

Ну как? Уловили суть? Тогда решаем самостоятельно.)

1. Найдите все значения параметра b, при которых уравнение

ax 2 + 3x +5 = 0

имеет единственный корень.

2. Найдите все значения параметра а, при каждом из которых больший корень уравнения

x 2 — (14a-9)x + 49a 2 — 63a + 20 = 0

3. Найдите все значения параметра а, при каждом из которых сумма квадратов корней уравнения

x 2 — 4ax + 5a = 0

4. Найдите все значения параметра а, при каждом из которых уравнение

x 2 + 2(a-2)x + a + 3 = 0

имеет два различных корня, расстояние между которыми больше 3.

Содержание

Love Soft
Инструменты пользователя
Инструменты сайта
Боковая панель
Навигация
Связь
Содержание
Квадратное уравнение. Парабола
Квадратичная функция
Vertex form
Квадратное уравнение
Теорема Виета
Применения теоремы Виета
Определение знаков корней
Геометрический смысл теоремы Виета
Обобщение теоремы Виета
Разность корней квадратного уравнения
Обобщение дискриминанта
Солнечные концентраторы
Подвесные мосты
Модель параболы
Парабола, как огибающая
Цепочки окружностей, вписанных в кривую 2-го порядка
Фокус и директриса параболы
Геометрический смысл параболы
Задача. Свободно падающее тело
Квадратные уравнения с параметрами
📽️ Видео

Видео:Быстрый способ решения квадратного уравненияСкачать

Love Soft

Инструменты пользователя

Инструменты сайта

Боковая панель

Содержание

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Квадратное уравнение. Парабола

Видео:Найти сумму корней квадратного уравнения, если дискриминант равен нулюСкачать

Квадратичная функция

$s=frac$ — путь, которое проходит свободно падающее тело за время t с нулевой начальной скоростью.

В общем виде эту зависимость можно записать так: $y=ax^2$. График этой функции — парабола, вершина которой находится в точке (0,0). Ветви направлены вверх. Четная функция.

Квадратичной называется функция, которую можно задать формулой y=ax² + bx + c, причем а отлично от 0. Здесь a,b,c — некоторые числа, x — переменная.

Корень — это значение переменной, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное равенство.

Vertex form

Можно выделить квадратный двучлен, поэтому это тоже парабола со сдвигом и растяжением.

Вершина параболы в точке (m,n), $m = frac, n = frac$

Видео:Формула корней квадратного уравнения с четным вторым коэффициентомСкачать

Квадратное уравнение

a — первый или старший коэффициент

b — второй коэффициент или средний или коэффициент при x

c — свободный член

Дискриминант $D = b^2-4ac$

Схематическое расположение параболы в зависимости от знаков первого коэффициента и дискриминанта.

Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент.

Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.

Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов кроме старшего (либо второй коэффициент, либо свободный член) равен нулю.

Видео:Дискриминант. Условия нахождения корней квадратного уравнения.Скачать

Теорема Виета

Теорема. Cумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Если приведенное квадратное уравнение $x^2 + px + q = 0$ имеет действительные корни, то их сумма равна $-p$, а произведение равно $q$, то есть

$$x_1 + x_2 = –p, \ x_1 cdot x_2 = q$$

Примечание. Любое квадратное уравнение можно привести к такому виду делением на a.

Пример. Найти сумму корней уравнения $x^2-7x+13=0$. Корней нет, поэтому ответ «сумма корней равна 7» — неверный. Для определения количества корней необходимо найти дискриминант.

Таким образом, в формулировку теоремы Виета необходимо добавить условие: если корни существуют, то … Или если дискриминант неотрицателен. Заметим, что при нулевом дискриминанте теорема Виета тоже работает (считать, что уравнение имеет два равных корня).

Пример. (Мерзляк, Алгебра 8 углубл, 2016)

Применения теоремы Виета

Теорема Виета позволяет угадывать целые корни квадратного трехчлена (не решая уравнение).

Так, находя корни квадратного уравнения x² – 5x + 6 = 0, можно начать с того, чтобы попытаться разложить свободный член (число 6) на два множителя так, чтобы их сумма равнялась бы числу 5. Это разложение очевидно: $$6 = 2 cdot 3, , 2 + 3 = 5. $$

Отсюда должно следовать, что числа 2 и 3 являются искомыми корнями.

Определение знаков корней

Определение знаков корней без решения уравнения (при условии что D > 0).

p > 0	p 0	Корни имеют одинаковые знаки
оба корня отрицательны	оба корня положительны
Свободный член q 0

Геометрический смысл теоремы Виета

Мы привыкли произносить «икс квадрат», «квадрат суммы», «удвоенный квадрат», не придавая этим выражениям геометрического смысла. На самом деле все они отражают взгляд на алгебру, который сложился еще в глубокой древности, потому что людям приходилось решать геометрические задачи на вычисление площадей.

В клинописных текстах древнего Вавилона (около 2000 лет до нашей эры) обнаружена такая задача. «Площадь 1000 состоит из суммы двух квадратов, и сторона меньшего составляет две трети стороны другого, уменьшенные на 10. Какова сторона бóльшего квадрата?»

Решить такую задачу — это все равно, что решить уравнение $x^2+(frac 2 3 x-10)^2=1000$. В клинописном тексте нет формулы для решения этого уравнения, но перечисляются необходимые этапы вычисления, которые приводят к корню $x = 30$.

Фактически вавилонский метод дает решение системы $beginx+y=p \ xy= qend$,

которая представляет собой запись задачи нахождения сторон прямоугольника с данным периметром и площадью. Теорема Виета, с изучения которой начинается этот параграф, связывает решение этой системы с решением квадратного уравнения.

Обобщение теоремы Виета

Теорема Вієта для зведеного многочлена $f(x)=x^n+a_x^+ldots+a_1x+a_0$ формулюється так: «Якщо $x_1, x_2, x_3, ldots, x_, x_n$ — всі комплексні корені (включаючи рівні) цього многочлена степеня n, то мають місце рівності:

$$ x_1+x_2+ldots+x_n=-a_ $$ $$ x_1x_2+x_1x_3+ldots+x_1x_n+x_2x_3+ldots+x_x_n=a_ $$ $$ x_1x_2x_3+x_1x_2x_4+ldots+x_1x_x_n+ldots+x_x_x_n=-a_ $$ $$x_1x_2x_3 ldots x_n=(-1)^n a_0$$

Разность корней квадратного уравнения

Для приведенного уравнения $$ x_1-x_2 = sqrt $$

$$ = x_1^2 — 2x_1x_2 + x_2^2 = (x_1+x_2)^2-4x_1x_2$$

Для приведенного уравнения с учетом теоремы Виета:

$$(x_1-x_2)^2 = (-b)^2-4c = b^2-4ac = D$$

Таким образом, если корни квадратного уравнения существуют, то расстояние между ними равно корню из дискриминанта. Грубо говоря, чем больше дискриминант, тем больше расстояние между корнями.

Обобщение дискриминанта

Дискриминантом многочлена $p(x)$ называется функция, задаваемая его коэффициентами.

Если точнее, то дискриминант — это произведение квадратов разностей корней многочлена, умноженное на старший коэффициент в степени на 2 меньше удвоенной степени многочлена.

1. Любая точка параболы равноудалена от некоторый точки, называемой фокусом параболы, и некоторой прямой, называемой ее директрисой.

2. Если вращать параболу вокруг ее оси симметрии (например, параболу $y = x^2$ вокруг оси Oy), то получается очень интересная поверхность, которая называется параболоидом вращения.

Поверхность жидкости, вращающейся в сосуде, имеет форму параболоида вращения. Вы можете увидеть эту поверхность, если помешаете ложечкой в неполном стакане чая, а потом вынете ложечку.

3. Если в пустоте бросить камень под некоторым углом к горизонту, то он полетит по параболе.

4. Если пересечь поверхность конуса плоскостью, параллельной какой-либо одной его образующей, то в сечении получится парабола.

5. В парках культуры устраивают иногда забавный аттракцион «Параболоид чудес». Каждому из стоящих внутри вращающегося параболоида кажется, что он стоит на полу, а остальные люди каким-то чудом держатся на стенках.

6. В зеркальных телескопах тоже применяют параболические зеркала: свет от далекой звезды, идущий параллельным пучком, упав на зеркало телескопа, собирается в фокусе.

7. У прожекторов зеркало обычно делается в форме параболоида. Если поместить источник света в фокусе параболоида, то лучи света, отразившись от параболического зеркала, образуют параллельный пучок.

Опыты, описанные в пунктах 2 и 5, основаны на одном и том же свойстве параболоида: если вращать параболоид с подходящей скоростью вокруг его оси, расположенной вертикально, то равнодействующая центробежной силы и силы тяготения в любой точке параболоида направлена перпендикулярно к его поверхности.

Солнечные концентраторы

Солнечные концентраторы используют энергию солнечной радиации, которая попадает на параболическую поверхность зеркала, в фокусе которой обычно располагается трубка с циркурирующим по ней теплоносителем. Как правило в качестве теплоносителя выступает масло. Теплоноситель нагревает воду, которая испаряясь поступает в турбогенератор в виде пара.

Параболические концентраторы с двигателем Стирлинга представляют собой СЭС с параболическими концентраторами, которые фокусируются на двигатель Стирлинга. Такие электростанции характеризуются высоким КПД (более 31%). В качестве рабочего тела двигателя Стирлинга используется, как правило, водород, или гелий.

Согласно известной исторической легенде, Архимед почти полностью сжег флот римского полководца Марка Марцелла, используя медные параболические зеркала.

8-этажное сооружение, включающее около 10 тысяч отдельных параболических зеркал. На сегодняшний день Солнечная Печь, выстроенная в 1970 году в Восточных Пиренеях – крупнейшая в мире. Массив зеркал действует в качестве параболического отражателя. Свет фокусируется в одном центре. И температура там может достигать 3500 градусов по Цельсию. При такой температуре можно плавить сталь. Но температуру можно регулировать, устанавливая зеркала под разными углами.

Подвесные мосты

Вантовый мост — тип висячего моста, состоящий из одного или более пилонов, соединённых с дорожным полотном посредством прямолинейных стальных тросов — вантов. В отличие от висячих мостов, где дорожное полотно поддерживается вертикальными тросами, прикреплёнными к протянутым по всей длине моста основным несущим тросам, у вантовых мостов тросы (ванты) соединяются непосредственно с пилоном.

Русский мост (Владивосток) — вантовый мост с самым длинным основным пролётом в мире (1104 м), при общей длине в 1886 м

Висячий мост — мост, в котором основная несущая конструкция выполнена из гибких элементов (кабелей, канатов, цепей и др.), работающих на растяжение, а проезжая часть подвешена.

Висячие мосты находят наиболее удачное применение в случае большой длины моста, невозможности или опасности установки промежуточных опор (например в судоходных местах).

Золотые Ворота (Сан-Франциско) — один из самых узнаваемых мостов в мире. Мост был самым большим висячим мостом в мире с момента открытия в 1937 году и до 1964 года. Общая длина моста — 2737 м, длина основного пролёта — 1280 м, высота опор — 227 м над водой, масса — 894 500 т. В среднем, по мосту проезжают сто тысяч автомобилей в сутки. 6 полос.

Основные несущие тросы (или цепи) подвешивают между установленными по берегам пилонами. К этим тросам крепят вертикальные тросы или балки, на которых подвешивается дорожное полотно основного пролёта моста. Основные тросы продолжаются за пилонами и закрепляются на уровне земли. Продолжение тросов может использоваться для поддержки двух дополнительных пролётов.

Под действием сосредоточенной нагрузки несущая конструкция может изменять свою форму, что уменьшает жёсткость моста. Для избежания прогибов в современных висячих мостах дорожное полотно усиливают продольными балками или фермами, распределяющими нагрузку.

Используются также конструкции, в которых дорожное полотно поддерживается системой прямолинейных канатов, закреплённых непосредственно на пилонах. Такие мосты называются вантовыми.

Основной пролёт можно сделать очень длинным при минимальном количестве материала. Поэтому использование такой конструкции очень эффективно при строительстве мостов через широкие ущелья и водные преграды. В современных висячих мостах широко применяют проволочные тросы и канаты из высокопрочной стали с пределом прочности около 2—2,5 ГПа(200-250 кгс/мм²), что существенно снижает собственный вес моста.

Отсутствует необходимость ставить промежуточные опоры, что даёт большие преимущества, например, в случае горных разломов или рек с сильным течением.

Будучи относительно податливыми, висячие мосты могут, без ущерба для целостности конструкции, изгибаться под действием сильного ветра или сейсмических нагрузок, тогда как более жёсткие мосты нужно строить более крепкими и тяжёлыми.

Полотно моста сильно прогибается, если на одном участке сосредоточена нагрузка существенно больше, чем на других. Из-за этого висячие мосты реже используются в качестве железнодорожных, чем другие типы.

Основные напряжения в висячем мосте — это напряжения растяжения в основных тросах и напряжения сжатия в опорах, напряжения в самом пролёте малы. Почти все силы в опорах направлены вертикально вниз и стабилизируются за счёт тросов, поэтому опоры могут быть очень тонкими. Сравнительно простое распределение нагрузок по разным элементам конструкции упрощает расчёт висячих мостов.

Под действием собственного веса и веса мостового пролёта тросы провисают и образуют дугу, близкую к параболе. Ненагруженный трос, подвешенный между двумя опорами, принимает форму т. н. «цепной линии», которая близка к параболе в почти горизонтальном участке. Если весом тросов можно пренебречь, а вес пролёта равномерно распределён по длине моста, тросы принимают форму параболы. Если вес троса сравним с весом дорожного полотна, то его форма будет промежуточной между цепной линией и параболой.

Клифтонский мост близ Бристоля (инженер Изамбард Кингдом Брюнель, 1864).

Акаси-Кайкё — самый длинный подвесной мост в мире. Полная длина составляет 3911 м. Пилоны имеют высоту 298 м, что выше 90-этажного дома.

Вначале были построены два бетонных основания для пилонов на дне пролива Акаси. Для строительства этого моста был разработан специальный бетон, который не растворяется в воде при заливке. Следующим этапом было протягивание тросов. Для этого нужно было с одного пилона на другой протянуть направляющий канат. Он был протянут с помощью вертолёта. Когда в 1995 году оба троса были протянуты, и можно было приступать к монтажу дорожного полотна, произошло непредвиденное: город Кобе стал жертвой крупного землетрясения магнитудой в 7,3 балла. Пилоны выдержали землетрясение, но из-за изменения рельефа дна пролива один из пилонов сдвинулся на 1 м в сторону, таким образом нарушив все расчёты. Инженеры предложили удлинить балки дорожного полотна и увеличить расстояние между вантами, свисающими с основных тросов. Строительные работы, задержанные не более чем на месяц, возобновились. Монтаж дорожного полотна закончился в 1998 году.

В конструкции моста имеется система двухшарнирных балок жёсткости, позволяющая выдерживать скорости ветра до 80 м/с, землетрясения магнитудой до 8,5 и противостоять сильным морским течениям. Для уменьшения действующих на мост нагрузок имеется система динамических гасителей колебаний.

Если вытянуть в длину все стальные нити (диаметром 5,23 мм) несущих тросов моста Акаси-Кайкё, то ими можно опоясать земной шар более семи раз.

Модель параболы

Легко получить параболу с помощью обычного карманного фонарика. Световое пятно от вертикально расположенного фонаря будет кругом. Немного повернём его, и пятно будет иметь форму эллипса. При дальнейшем повороте фонарика эллипс будет всё больше и больше вытягиваться, а в некоторый момент его наиболее удалённая точка уйдёт в бесконечность. Кривая, ограничивающая такое пятно, называется параболой. Неограниченные кривые, которые получаются при дальнейшем вращении фонарика, называются гиперболами. Все получившиеся кривые – окружность, эллипс, парабола, гипербола – конические сечения. Такое название они получили заслуженно, поскольку световой столб, выходящий из фонарика, является конусом.

Парабола, как огибающая

Параболу можно рассматривать, как огибающую семейства прямых.

См. также Конические сечения — Параболическое зеркало. Параболический бильярд

Цепочки окружностей, вписанных в кривую 2-го порядка

Если радиус окружности, вписанной в параболу $y=x^2$ равен 1, то радиус второй окружности, вписанной в эту же параболу и касающейся первой окружности, равен 2, радиус аналогичной 3-й окружности равен 3 и т. д.

Интересно, что радиусы подобной цепочки окружностей, вписанных в угол, образуют геометрическую прогрессию.

Видео:Корни квадратного уравнения общего вида.Скачать

Фокус и директриса параболы

Задача. Постройте график функции $y = x^2$. Масштаб возьмите покрупней: 1 = 4 клетки. Отметьте на оси Oy точку F(0; 1/4). Полоской бумаги измерьте расстояние от точки F до какой-нибудь точки M параболы. Затем приколите полоску в точке M и поверните ее вокруг этой точки так, чтобы она стала вертикальной. Конец полоски опустится немного ниже оси абсцисс. Отметьте на полоске, насколько она выйдет за ось абсцисс. Возьмите теперь другую точку на параболе и повторите измерение еще раз. Насколько теперь опустился край полоски за ось абсцисс?

Результат мы Вам сможем сказать заранее: какую бы точку на параболе вы ни взяли, расстояние от этой точки до точки (0; 1/4) будет больше расстояния от той же точки до оси абсцисс всегда на одно и то же число — на 1/4. Можно сказать иначе: расстояние от любой точки параболы $y = x^2$ до точки (0; 1/4) равно расстоянию от той же точки параболы до прямой y = −1/4, параллельной оси Ox.

Замечательная точка F(0; 1/4) называется фокусом параболы, а прямая y = −1/4 — директрисой (по-русски направляющая) этой параболы. Директриса и фокус есть у всякой параболы.

Видео:Алгебра 8 класс. Ещё одна формула корней квадратного уравненияСкачать

Геометрический смысл параболы

Парабола — это множество точек, равноудалённых от данной прямой (директрисы параболы) и не лежащей на директрисе данной точки (фокуса параболы).

Парабола — это множество центров окружностей, касающихся данного круга и данной прямой, касающейся этого круга.

Источник — подробнее, больше картинок

Видео:Откуда взялись ФОРМУЛЫ КОРНЕЙ квадратного уравнения? | МатематикаСкачать

Задача. Свободно падающее тело

Тело, свободно падающее без начальной скорости с некоторой высоты, за последнюю секунду падения проходит путь в 7 раз больший чем за первую секунду движения. Найдите высоту, с которой падает тело.

За первую секунду тело пройдёт расстояние равное: $S=frac=10 cdot 1/2=5 $ м.

Тогда за последнюю секунду тело пройдёт расстояние равное 35 м. С другой стороны, за последнюю секунду тело пройдет расстояние: $$ frac — frac= 35$$

Решив это уравнение получим t = 4 с, откуда S = 80 м

t, с	1	2	3	4	5	6
s общий, м	5	20	45	80	125	180
s за последнюю секунду	5	15=20-5	25=45-20	35=80-45	45=125-80	55

Таким образом, любое падающее тело за первую секунду проходит 5м, за вторую секунду — в 3 раза больше, за третью — в 5 раз больше, за четвертую — в 7 раз больший путь, за пятую — в 9 раз, за шестую — в 11 раз. Арифметическая прогрессия, физики называют это закон нечетных чисел. Путь, пройденный за секунду, тоже образует арифметическую прогрессию с разность 10, что соответствует ускорению свободного падения g.

Задача. Тело, падающее без начальной скорости, за последнюю секунду падения прошло путь s = 35 м. Какую скорость имело тело в момент падения на землю? Сопротивлением воздуха пренебречь.

Решение. Время падения = 4 с. Скорость $v = s’ = gt = 40$ м/с.

Видео:Параметры | Начало #4 (квадратное уравнение)Скачать

Квадратные уравнения с параметрами

Ханты-Мансийский автономный округ — Югра

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа №4»

Индекс 628681 Российская Федерация, Тюменская область, Ханты-Мансийский автономный округ – Югра, г. Мегион, /1

Cайт: http//www. megionschool4.ru

Департамент финансов администрации города Мегиона

( МБОУ «Средняя общеобразовательная школа №4»

р/с в РКЦ г. Нижневартовска,

Квадратные уравнения с параметрами

(Методическая разработка для учащихся 9-11 классов)

учитель математики высшей квалификационной категории,

заместитель директора по УВР

1.Теоремы о расположении корней квадратного трехчлена

§2.Применение теоремы Виета

3.Примеры решения задач для подготовки к ГИА и ЕГЭ по математике

Список рекомендованной литературы

В методической разработке систематизированы теоремы о расположении корней квадратного трехчлена (необходимые и достаточные условия расположения корней квадратичной функции относительно заданных точек); особое внимание уделено использованию свойств квадратичной функции; приведено применение теоремы Виета к решению квадратных уравнений с параметрами; все идеи проиллюстрированы примерами, рассмотрены основные методы решения квадратных уравнений с параметрами, подробные методические указания по решению квадратных уравнений с параметрами.

Методическая разработка предназначена для учащихся 9-11 классов, студентов педагогических вузов, а также для учителей. Пособие поможет в подготовке к вступительному экзамену в вуз, сдаче ЕГЭ по математике и к ГИА в новой форме.

Разработка посвящена одному из наиболее трудных разделов элементарной математики: задачам с параметрами. В последние годы в тестах ЕГЭ и ГИА по математике, и на вступительных экзаменах в высшие учебные заведения широкое распространение получили задачи, содержащие параметры. Решение задач с параметрами носит учебно-исследовательский характер, они играют важную роль в формировании логического мышления, развитии творческих способностей учащихся, в формировании научно-исследовательских умений. Задачи с параметрами представляют собой как бы небольшую модель будущей научной работы учащегося. В задачах с параметрами содержится множество приёмов, необходимых не только для математического развития личности, но и и в любом другом научном исследовании. Поэтому решение задач с параметрами и в частности решение квадратных уравнений с параметрами является пропедевтикой научно-исследовательской работы учащихся. На ЕГЭ по математике (часто задания С5), ГИА (задания части 2) и на вступительных экзаменах встречаются, в основном, два типа задач с параметрами. Первый: «Для каждого значения параметра найти все решения некоторого уравнения или неравенства». Второй: «Найти все значения параметра, при каждом из которых для данного уравнения или неравенства выполняются некоторые условия». Соответственно и ответы в задачах этих двух типов различаются по существу. В ответе к задаче первого типа перечисляются все возможные значения параметра и для каждого из этих значений записываются решения уравнения. В ответе к задаче второго типа указываются все значения параметра, при которых выполняются условия, указанные в задаче.

Как известно, решению задач с параметрами в школе уделяется очень мало внимания. Поэтому решение задач с параметрами всегда вызывает большие трудности у учащихся; трудно рассчитывать на то, что учащиеся, подготовка которых не содержала «параметрическую терапию», смогут в жесткой атмосфере конкурсного экзамена успешно справиться с подобными задачами, следовательно, учащиеся должны специально готовиться к «встрече с параметрами». Многие учащиеся воспринимают параметр как «обычное» число. Действительно, в некоторых задачах параметр можно считать постоянной величиной, но это постоянная величина принимает неизвестные значения. Поэтому необходимо рассматривать задачу при всех возможных значениях этой постоянной величины. В других задачах бывает удобно искусственно объявить параметром одну из неизвестных.

Задачи с параметрами обладают диагностической и прогностической ценностью – с помощью задач с параметрами можно проверить знание основных разделов школьной математики, уровень математического и логического мышления, первоначальные навыки научно-исследовательской деятельности, а главное, перспективные возможности успешного овладения курсом математики данного вуза.

Анализ вариантов ЕГЭ по математике и вступительных экзаменов в различные вузы показывает, что большинство предлагаемых задач с параметрами связано с расположением корней квадратного трехчлена. Будучи основной в школьном курсе математики, квадратичная функция формирует обширный класс задач с параметрами, разнообразных по форме и содержанию, но объединенных общей идеей – в основе их решения лежат свойства квадратичной функции. При решении таких задач рекомендуется работать с тремя типами моделей:

1. вербальная модель – словесное описание задачи;

2. геометрическая модель – эскиз графика квадратичной функции;

3. аналитическая модель – система неравенств, при помощи которой описывается геометрическая модель.

Методическое пособие содержит теоремы о расположении корней квадратного трехчлена (необходимые и достаточные условия расположения корней квадратичной функции относительно заданных точек), применение теоремы Виета к решению квадратных уравнений с параметрами. Приведены подробные решения 15 задач с методическими рекомендациями. Назначение данного пособия – помочь выпускнику и учителю математики в подготовке к сдаче ЕГЭ и ГИА по математике, и вступительного экзамена в вуз в виде теста или в традиционной форме.

1. Теоремы о расположении корней квадратного трехчлена

Теоремы о расположении корней квадратного трехчлена не входят непосредственно ни в школьную программу по математике, ни в программу для поступающих в вузы, поэтому выпускник или абитуриент, пользуясь ими, вообще говоря, должен уметь их доказывать. В то же время, обоснование теорем о расположении корней квадратного трехчлена строится на элементарных фактах школьной математики. В данном пособии приведены доказательства нескольких теорем.

Введем следующие обозначения: х1, х2 – корни квадратного трехчлена f(x), х1 ≤ х2, D – дискриминант f(x), xb – абсцисса вершины параболы, являющейся графиком f(x). Решение большинства задач с параметром, в которых необходимо провести исследование квадратного трехчлена, сводится к определению необходимых и достаточных условий реализации одного или нескольких из следующих случаев:

Теорема 1.Для того чтобы оба корня квадратного трехчлена f(x) = ax2 + bx + c (a ≠ 0) были больше некоторого числа n,необходимо и достаточно выполнение следующих условий:

Геометрическая интерпретация. Для того чтобы парабола (см. рис. 1, 2) – график функции f(x) = ax2 + bx + c – пересекала ось ОХ в точках (х1; 0) и (х2; 0), лежащих правее точки (n; 0), необходимо и достаточно выполнения трех условий:

1. вершина параболы – либо лежит в нижней полуплоскости, либо в верхней полуплоскости, либо на оси ОХ ( условие D≥0);

2. ось симметрии параболы – прямая хb = — — лежит правее прямой х = n ( условие xb>n );

3. парабола пересекается с прямой х = n в точке, лежащей в верхней полуплоскости при a>0 и в точке, лежащей в нижней полуплоскости при а 0).

Рис. 1

Доказательство теоремы 1.

Достаточность. Так как D ≥ 0,то по теореме о дискриминанте, получим, что квадратный трехчлен имеет два корня х1 и х2; пусть х1≤х2. Так как вершина параболы расположена между корнями трехчлена, т. е.х1≤хв≤х2, и, по условию, n 0 и уже доказанное неравенство х2 > n:

f(n) = a∙(n – x1)∙(n – x2).

Сравнение знаков левой и правой частей этого неравенства приводит нас к выводу, что выполнено неравенство n – х1 n.

Необходимость. Так как трехчлен имеет два корня, то по теореме о дискриминанте, D≥0. Так как х1> n и х2> n, то х1+х2 > 2n, поэтому

хв = > = n.

По теореме о разложении на линейные множители, с учетом известных по условию знаков, получим запись f(n) = a∙(n – x1)∙(n – x2), из которой следует, что f(n) > 0. Тем самым теорема доказана полностью.

Теорема 2. Для того чтобы оба корня квадратного трехчлена f(х) были меньше некоторого числа m, необходимо и достаточно выполнение следующих условий:

Рис. 3

Рис. 4

Теорема 3.Для того чтобы оба корня квадратного трехчлена f(x) принадлежали заданному промежутку (n; m), необходимо и достаточно выполнение следующих условий:

Рис. 5

Рис. 6

Теорема 4. Только меньший корень квадратного трехчлена f(x) принадлежит заданному промежутку (n; m) тогда и только тогда, когда одновременно выполняются условия:

Рис. 7

Теорема 5. Только больший корень квадратного трехчлена f(x) принадлежит заданному промежутку (n; m) тогда и только тогда, когда одновременно выполняются условия:

Рис. 8

Теорема 6. Для того чтобы оба корня квадратного трехчлена f(x) лежат вне заданного промежутка (n; m), необходимо и достаточно выполнение следующих условий:

Рис. 9

Теорема 7.Для того чтобы один из корней квадратного трехчлена f(x) был больше заданного числа n, а другой меньше, необходимо и достаточно выполнение условия (или для того чтобы некоторое число n лежало между корнями квадратного трехчлена, необходимо и достаточно выполнение условия):

Рис. 10

Теорема 8. Квадратный трехчлен f(x) имеет один корень внутри интервала (n;m), а другой расположен вне этого интервала тогда и только тогда, когда выполняется условие f(n)∙f(m) 6 дискриминант оказывается отрицательным, следовательно, квадратное уравнение не имеет корней.

Ответ: при уравнение не имеет корней; при а = 1 уравнение имеет один корень х = -1; при уравнение имеет два корня ; при а = 2 уравнение имеет единственный корень ; при а = 6 уравнение имеет единственный корень .

Пример 2.При каком значении параметра а уравнение (а — 2)х2 + (4 – 2а)х + 3 = 0 имеет единственный корень?

Решение. Если а = 2, то уравнение превращается в линейное∙х + 3 = 0; которое не имеет корней.

Если а ≠ 2, то уравнение – квадратное и имеет единственный корень при нулевом дискриминанте D.

D = 0 при а1 = 2 и a2 = 5. Значение а = 2 исключается, так как противоречит условию, что исходное уравнение – квадратное.

4.При каких значениях параметра а квадратное уравнение

(а — 1)х2 + (2а + 3)х + а + 2 = 0 имеет корни одного знака?

Решение. Так как по условию задачи рассмотренное уравнение – квадратное, значит, а ≠ 1. очевидно, условие задачи предполагает также существование корней квадратного уравнения, что означает неотрицателность дискриминанта

Так как по условию корни должны быть одинаковых знаков, то х1∙х2 > 0, т. е. .Решением последнего неравенства является .С учетом условий D ≥ 0 и а ≠ 1 получим .

Ответ: .

Пример 3.Найти все значения а, для которых уравнение х2 – 2(а – 1)х + (2а + 1) = 0 имеет два положительных корня.

Решение. Из теоремы Виета для того чтобы оба корня х1 и х2 данного уравнения были положительными, необходимо и достаточно, чтобы дискриминант квадратного трехчлена х2 – 2(а – 1)х + (2а + 1) был неотрицательным, а произведение х1∙х2 и сумма х1 + х2 были положительными. Получаем, что все а, удовлетворяющие системе

И только они, являются решениями поставленной задачи. Э та система равносильна системе

Решением которой, а следовательно, и самой задачи являются все числа из промежутка [4; + ∞).

Пример 4.При каких значениях параметра а уравнение (а — 2)х2 — 2(а + 3)х + 4а = 0

имеет два корня, один из которых меньше 2, а другой больше 3?

Решение. По теореме 6, для того чтобы оба корня данного квадратного трехчлена лежали вне заданного промежутка, необходимо и достаточно выполнение условий Получим систему неравенств:

Ответ: .

Пример 5.При каких значениях а уравнение (а — 1)∙х2 = (а + 1)∙х – а имеет единственное решение, удовлетворяющее условию 0 х1. Искомые значения параметра а удобнее найти, решив систему неравенств:

Рис.18 0 х1 2 3 х2 5 х

Ответ: (1;3)

Пример 8.При каких значениях параметра а один корень уравнения ах4 – (а — 3)х2 + 3а = 0 меньше –2, три остальных больше –1?

Решение. Пусть х2 = t. Исходя из требований, предъявляемых к корням исходного уравнения, достаточно решить следующую задачу: при каких значениях а один корень уравнения at2 – (a — 3)t + 3a = 0 больше 4, другой меньше 1, но не меньше 0? Очевидно а ¹ 0, D > 0. Представим уравнение в виде:

Его корни будут удовлетворять указанным выше условиям, если f(1) 0. Поскольку f(0) = 3, то достаточно решить систему

Решением уравнения является . Ответ: .

Пример 9.Найдите все значения параметра а, при которых все корни уравнения

(2 — а)х2 – 3ах + 2а = 0 больше .

Решение. Введем обозначения f(x) = (2 — a)x2 – 3ax + 2a, ;

Если а = 2, то . для случая а ≠ 2, чтобы сформулировать нужные условия, представим себе график трехчлена f(x), оба корня которого больше .

(к рис.19) (к рис.20)

(к рис.21) (к рис.22)

Объединяя эти условия, получим систему:

Ответ: .

Пример 10. Найти все значения а, при которых уравнение cos8x + sin8x = a имеет корни, и решить это уравнение.

Решение. Используя равенства cos8x + sin8x = (cos4x – sin4x)2 + 2cos4x×sin4x = cos22x + и полагая cos 4x = t, преобразуем исходное уравнение к виду t2 + 14t + 17 – 32a = 0. Задача сводится к нахождению тех значений а при которых последнее уравнение имеет действительные корни такие, что хотя один из них удовлетворяет условию . Имеем дискриминант уравнения: