Как найти расстояние между двумя прямыми на плоскости заданными уравнениями

В этой статье дано определение расстояния между двумя параллельными прямыми на плоскости и в трехмерном пространстве, а также разобран метод координат, позволяющий вычислять расстояние между параллельными прямыми. Сначала приведена необходимая теория, после чего приведены подробные решения примеров и задач, в которых находится расстояние между двумя параллельными прямыми.

Навигация по странице.

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Расстояние между двумя параллельными прямыми – определение.

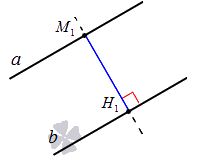
Определение расстояния между двумя параллельными прямыми дается через расстояние от точки до прямой.

Расстояние между двумя параллельными прямыми – это расстояние от произвольной точки одной из параллельных прямых до другой прямой.

Для наглядности изобразим две параллельные прямые a и b , отметим на прямой а произвольную точку М₁ , опустим перпендикуляр из точки М₁ на прямую b , обозначив его H₁ . Отрезок М₁H₁ соответствует расстоянию между параллельными прямыми a и b .

Приведенное определение расстояния между двумя параллельными прямыми справедливо как для параллельных прямых на плоскости, так и для прямых в трехмерном пространстве. Более того, такое определение расстояния между двумя параллельными прямыми принято не случайно. Оно тесно связано со следующей теоремой.

Все точки одной из двух параллельных прямых удалены на одинаковое расстояние от другой прямой.

Рассмотрим параллельные прямые a и b . Отметим на прямой a точку М₁ , опустим из нее перпендикуляр на прямую b . Основание этого перпендикуляра обозначим как H₁ . Тогда длина перпендикуляра М₁H₁ есть расстояние между параллельными прямыми a и b по определению. Докажем, что равно , где М₂ – произвольная точка прямой a , отличная от точки M₁ , а H₂ – основание перпендикуляра, проведенного из точки М₂ на прямую b . Доказав этот факт, мы докажем и саму теорему.

Так как внутренние накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей, равны (об этом говорилось в статье параллельные прямые, параллельность прямых), то , а прямая M₂H₂ , перпендикулярная прямой b по построению, перпендикулярна и прямой a . Тогда треугольники М₁H₁H₂ и М₂М₁H₂ прямоугольные, и, более того, они равны по гипотенузе и острому углу: М₁H₂ – общая гипотенуза, . Из равенства треугольников следует равенство их соответствующих сторон, поэтому, . Теорема доказана.

Следует заметить, что расстояние между двумя параллельными прямыми является наименьшим из расстояний от точек одной прямой до точек другой прямой.

Видео:Видеоурок "Расстояние между прямыми в пространстве"Скачать

Нахождение расстояния между параллельными прямыми – теория, примеры, решения.

Итак, нахождение расстояния между параллельными прямыми сводится к нахождению длины перпендикуляра, проведенного из некоторой точки одной из прямых на другую прямую. При этом подбирается метод, позволяющий это расстояние отыскать. Выбор метода зависит от условий конкретной задачи. В некоторых случаях можно использовать теорему Пифагора, в других — признаки равенства или подобия треугольников, определения синуса, косинуса или тангенса угла и т.п. Если же параллельные прямые заданы в прямоугольной системе координат, то расстояние между заданными параллельными прямыми можно вычислить методом координат. На нем и остановимся.

Сформулируем условие задачи.

Пусть на плоскости или в трехмерном пространстве зафиксирована прямоугольная система координат, заданы две параллельные прямые a и b и требуется найти расстояние между этими прямыми.

Решение этой задачи строится на определении расстояния между параллельными прямыми — чтобы найти расстояние между двумя заданными параллельными прямыми нужно:

• определить координаты некоторой точки М₁ , лежащей на прямой a (или на прямой b );
• вычислить расстояние от точки М₁ до прямой b (или a ).

С определением координат точки М₁ , лежащей на какой-нибудь из заданных параллельных прямых, проблем не возникнет, если, конечно, Вам знакомы основные виды уравнения прямой на плоскости и уравнения прямой в пространстве. Для нахождения расстояния от точки М₁ до нужной из заданных параллельных прямых Вам будет полезна информация из раздела нахождение расстояния от точки до прямой.

В частности, если в прямоугольной системе координат Oxy на плоскости прямую a задает общее уравнение прямой вида , а прямую b , параллельную прямой a , — общее уравнение прямой , то расстояние между этими параллельными прямыми можно вычислить по формуле .

Покажем вывод этой формулы.

Возьмем точку , которая лежит на прямой a , тогда координаты точки М₁ удовлетворяют уравнению , то есть, справедливо равенство , откуда имеем .

Если , то нормальное уравнение прямой b имеет вид , а если , то нормальное уравнение прямой b имеет вид . Тогда при расстояние от точки до прямой b вычисляется по формуле , а при — по формуле

То есть, при любом значении С₂ расстояние от точки до прямой b можно вычислить по формуле . А если учесть равенство , которое было получено выше, то последняя формула примет вид . На этом вывод формулы для вычисления расстояние между двумя параллельными прямыми, заданными общими уравнениями прямых вида и завершен.

Разберем решения примеров.

Начнем с нахождения расстояния между двумя параллельными прямыми, заданными в прямоугольной системе координат Oxy на плоскости.

Найдите расстояние между параллельными прямыми и .

Очевидно, что прямая, которой соответствуют параметрические уравнения прямой на плоскости вида , проходит через точку .

Искомое расстояние между параллельными прямыми равно расстоянию от точки до прямой . Вычислим его.

Получим нормальное уравнение прямой, которой отвечает уравнение прямой с угловым коэффициентом вида . Для этого сначала запишем общее уравнение прямой: . Теперь вычислим нормирующий множитель: . Умножив на него обе части последнего уравнения, имеем нормальное уравнение прямой: . Искомое расстояние равно модулю значения выражения , вычисленного при . Итак, расстояние между заданными параллельными прямыми равно

Второй способ решения.

Получим общие уравнения заданных параллельных прямых.

Выше мы выяснили, что прямой соответствует общее уравнение прямой . Перейдем от параметрических уравнений прямой вида к общему уравнению этой прямой:

Коэффициенты при переменных x и y в полученных общих уравнениях параллельных прямых равны, поэтому мы сразу можем применить формулу для вычисления расстояния между параллельными прямыми на плоскости: .

.

На плоскости введена прямоугольная система координат Oxy и даны уравнения двух параллельных прямых и . Найдите расстояние между указанными параллельными прямыми.

Канонические уравнения прямой на плоскости вида позволяют сразу записать координаты точки М₁ , лежащей на этой прямой: . Расстояние от этой точки до прямой равно искомому расстоянию между параллельными прямыми. Уравнение является нормальным уравнением прямой, следовательно, мы можем сразу вычислить расстояние от точки до прямой : .

Второй способ решения.

Общее уравнение одной из заданных параллельных прямых нам уже дано . Приведем каноническое уравнение прямой к общему уравнению прямой: . Коэффициенты при переменной x в общих уравнениях заданных параллельных прямых равны (при переменной y коэффициенты тоже равны — они равны нулю), поэтому можно применять формулу, позволяющую вычислить расстояние между заданными параллельными прямыми: .

Осталось рассмотреть пример нахождения расстояния между параллельными прямыми в трехмерном пространстве.

Найдите расстояние между двумя параллельными прямыми, которым в прямоугольной системе координат Oxyz соответствуют канонические уравнения прямой в пространстве вида и .

Очевидно, прямая проходит через точку . Вычислим расстояние от этой точки до прямой — оно даст нам искомое расстояние между параллельными прямыми.

Прямая проходит через точку . Обозначим направляющий вектор прямой как , он имеет координаты . Вычислим координаты вектора (при необходимости смотрите статью координаты вектора по координатам точек): . Найдем векторное произведение векторов и :

Теперь осталось применить формулу, позволяющую вычислить расстояние от точки до прямой в пространстве: .

расстояние между заданными параллельными прямыми равно .

Видео:Расстояние между параллельными прямымиСкачать

Расстояние между прямыми на плоскости онлайн

С помощю этого онлайн калькулятора можно найти расстояние между прямыми на плоскости. Дается подробное решение с пояснениями. Для вычисления расстояния между прямыми, задайте вид уравнения прямых («канонический», «параметрический» или «общий»), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Расстояние между прямыми на плоскости − теория, примеры и решения

• Содержание
• 1. Расстояние между прямыми в каноническом виде.
• 2. Расстояние между прямыми в общем виде.

1. Расстояние между прямыми в каноническом виде.

Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L₁ и L₂:

.

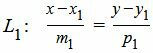(1)

,

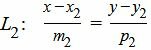(2)

Прямые (1) и (2) могут совпадать, быть паралленьными или пересекаться. Если прямые пересекаются, то понятие расстояния между ними не имеет смысла (не определено). Если прямые совпадают, то расстояние между ними равно нулю. Если же они параллельны, то расстояние между ними можно вычислить следующими методами:

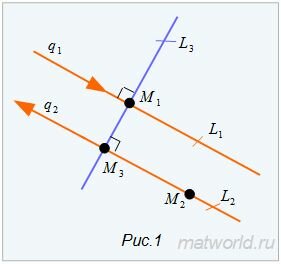Рассмотрим этот метод подробнее. Каноническое уравнение прямой L₃, проходящей через точку M₁(x₁, y₁) имеет следующий вид:

,

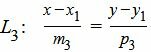(3)

Для того, чтобы прямая L₃ была перпендикулярна прямой L₂, направляющие векторы этих прямых должны быть ортогональны, т.е. скалярное произведение этих векторов должен быть равным нулю:

,

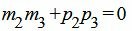(4)

Так как направляющий вектор прямой не может быть равным нулю, то предположим, что координата m₂ вектора q₂ отлична от нуля. Тогда в качестве вектора q₃ можно взять вектор q₃=<m₃, p₃>=<p₂, −m₂>. Следовательно, уравнение прямой L₃ получит следующий вид:

,

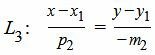(5)

Для вычисления координат точки пересечения прямых L₂ и L₃, решим систему линейных уравнений (2) и (5). Преобразуем эти уравнения сделав перекрестное умножение:

Откроем скобки и перенесем налево переменную y:

Запишем (6) и (7) в матричном виде:

,

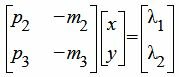(8)

,

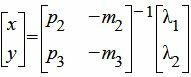(11)

Для построения обратной матрицы воспользуемся методом алгебраических дополнений. Сначала вычислим определитель матрицы:

.

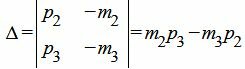Тогда обратная матрица примет следующий вид:

.

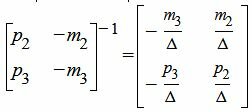(12)

Подставляя значение обратной матрицы (12) в (11), получим:

.

.

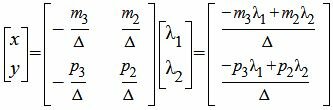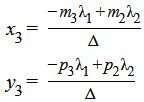(13)

Расстояние между точками M₁ и M₃ равно:

.

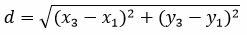(14)

Полученное расстояние d также является расстоянием между прямыми L₁ и L₂.

Пример 1. Найти расстояние между прямыми L₁ и L₂:

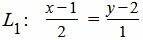(15)

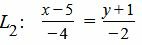(16)

Пользуясь формулой (5), построим уравнение прямой L₃, проходящей через точку M₁ и перпендикулярной прямой L₂:

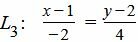(17)

Для вычисления координат точки пересечения прямых L₂ и L₃, решим систему линейных уравнений (16) и (17). Преобразуем эти уравнения сделав перекрестное умножение:

Сделаем эквивалентные преобразования:

Запишем систему линейных уравнений (18)-(19) в матричном виде:

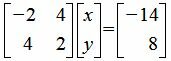Вычислим вектор (x, y) T :

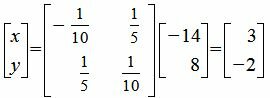Получили точку M₃(x₃, y₃)=(3, −2), которая является точкой пересечения прямых L₂ и L₃. Расстояние между прямыми L₁ и L₂ равно расстоянию между точками M₁ и M₃. Вычислим это расстояние:

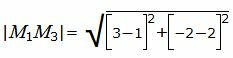Ответ: Расстояние между прямыми L₁ и L₂ равно d=4.47213595.

Метод 2. Найдем расстояние между прямыми L₁ и L₂ (уравнения (1) и (2)). Уравнение прямой L₃ в общем виде, проходящей через точку M₁ и перпендикулярной прямой L₂ имеет следующий вид:

Для того, чтобы прямая L₃ была перпендикулярна прямой L₂, нормальный вектор n₃=<A₃, B₃> прямой L₃ должен быть коллинеарным направляющему вектору q₂ прямой L₂. Поэтому в качестве нормального вектора прямой L₃ можно взять вектор q₂=<m₂, p₂>. Подставим координаты вектора q₂ в (20):

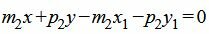(21)

Приведем уравнение прямой (2) к параметрическому виду:

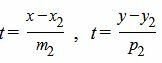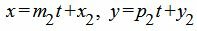(22)

Подставим (22) в (21) и решим относительно t:

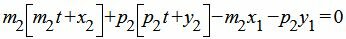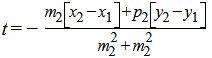(23)

Мы получили такое значение t, при котором соответствующая точка на прямой L₂ удовлетворяет уравнению прямой L₃, т.е. находится на этой прямой (является точкой пересечения прямых L₂ и L₃). Подставляя значение t в (22), получим координаты точки M₃(x₃, y₃). Далее вычисляем расстояние между точками M₁ и M₃:

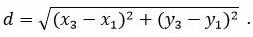(24)

Пример 2. Найти расстояние между прямыми

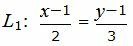(25)

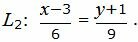(26)

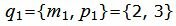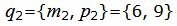Уравнение прямой L₃, проходящей через точку M₁ и имеющий нормальный вектор n₃=<A₃, B₃> представляется формулой:

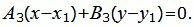(27)

Для того, чтобы прямая L₃ была перпендикулярна прямой L₂, нормальный вектор n₃=<A₃, B₃> прямой L₃ должен быть коллинеарным направляющему вектору q₂ прямой L₂. Поэтому в качестве нормального вектора прямой L₃ можно взять вектор q₂=<m₂, p₂>=. Подставим координаты вектора q₂ и координаты точкиM₁ в (27):

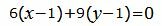После упрощения получим уравнение прямой L₃, проходящей через точку M₁ и перпендикулярной прямой L₂:

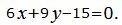(28)

Для нахождения точки пересечения прямых L₂ и L₃ проще всего пользоваться параметрическим уравнением прямой L₂. Составим параметрическое уравнение прямой L₂:

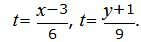Выразим переменные x, y через параметр t :

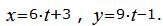(29)

Подставим значения x, y из выражения (29) в (28) и решим относительно t:

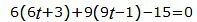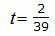Подставляя значение t в выражения (29), получим координаты точки M₃:

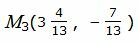Вычислим расстояние между точками M₁ и M₃

Ответ. Расстояние между прямыми L₁ и L₂ равно:

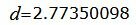2. Расстояние между прямыми в общем виде.

Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы параллельные прямые L₁ и L₂:

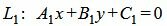(30)

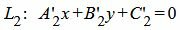(31′)

где n₁=<A₁, B₁> и n₂=<A₂, B₂> − направляющие векторы прямых L₁ и L₂, соответственно. Так как прямые параллельны, то можно один из них умножить на какое-то число так, чтобы нормальные векторы этих прямых совпадали. Пусть A₂≠0. Умножим (31′) на A₁/A’₂. Тогда уравнение (2′) примет следующий вид:

(31)

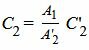Покажем, что расстояние между прямыми L₁ и L₂ равно:

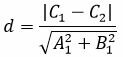(32)

Метод 1. Пусть A₁≠0. Тогда точка M₁(x₁, y₁)=M₁(−C₁/A₁, 0) принадлежит прямой L₁. Это легко проверить, подставив координаты точки M₁ в (30). Построим уравнение прямой, проходящей через точку M₁ и перпендикулярной прямой L₂:

Поскольку прямая L₃ перпендикулярна прямой L₂, то нормальные векторы этих прямых ортогональны. Тогда вместо нормального вектора n₃=<A₃, B₃> прямой L₃ можно взять вектор, ортогональный нормальному вектору n₂, т.е. вектор n₃=<B₁, −A₁> (так как скалярное произведение этих векторов равно нулю). Тогда имеем:

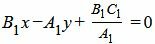(34)

Найдем точку пересечения прямых L₂ и L₃. Для этого решим систему линейных уравнений (31),(34), представляя в матричном виде:

,

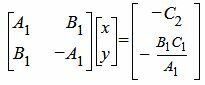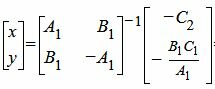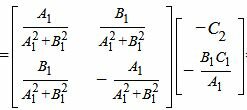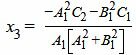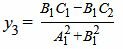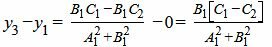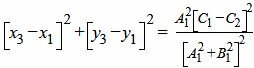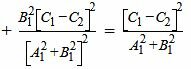Наконец, расстояние между точками M₁ и M₃, и следовательно, расстояние между прямыми L₁ и L₂ равно:

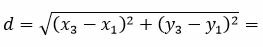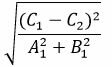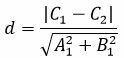(35)

Метод 2. Воспользуемся понятием отклонения точки от прямой. Пусть M₁(x₁, y₁) точка, принадлежащая прямой (30), Тогда выполняется равенство

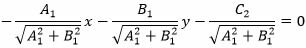При С₂ Пример 3. Найти расстояние между прямыми

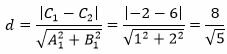Ответ. Расстояние между прямыми L₁ и L₂ равно:

Видео:§16 Угол между двумя прямыми на плоскостиСкачать

Расстояние между двумя параллельными прямыми: определение и примеры нахождения

В материале этой статьи разберем вопрос нахождения расстояния между двумя параллельными прямыми, в частности, при помощи метода координат. Разбор типовых примеров поможет закрепить полученные теоретические знания.

Видео:Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Расстояние между двумя параллельными прямыми: определение

Расстояние между двумя параллельными прямыми – это расстояние от некоторой произвольной точки одной из параллельных прямых до другой прямой.

Приведем иллюстрацию для наглядности:

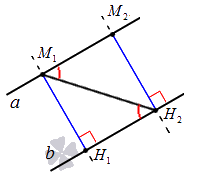
На чертеже изображены две параллельные прямые a и b . Точка М 1 принадлежит прямой a , из нее опущен перпендикуляр на прямую b . Полученный отрезок М 1 Н 1 и есть расстояние между двумя параллельными прямыми a и b .

Указанное определение расстояния между двумя параллельными прямыми справедливо как на плоскости, так и для прямых в трехмерном пространстве. Кроме того, данное определение взаимосвязано со следующей теоремой.

Когда две прямые параллельны, все точки одной из них равноудалены от другой прямой.

Пусть нам заданы две параллельные прямые a и b . Зададим на прямой а точки М 1 и М 2 , опустим из них перпендикуляры на прямую b , обозначив их основания соответственно как Н 1 и Н 2 . М 1 Н 1 – это расстояние между двумя параллельными прямыми по определению, и нам необходимо доказать, что | М 1 Н 1 | = | М 2 Н 2 | .

Пусть будет также существовать некоторая секущая, которая пересекает две заданные параллельные прямые. Условие параллельности прямых, рассмотренное в соответствующей статье, дает нам право утверждать, что в данном случае внутренние накрест лежащие углы, образованные при пересечении секущей заданных прямых, являются равными: ∠ M 2 M 1 H 2 = ∠ H 1 H 2 M 1 . Прямая М 2 Н 2 перпендикулярна прямой b по построению, и, конечно, перпендикулярна прямой a . Получившиеся треугольники М 1 Н 1 Н 2 и М 2 М 1 Н 2 являются прямоугольными и равными друг другу по гипотенузе и острому углу: М 1 Н 2 – общая гипотенуза, ∠ M 2 M 1 H 2 = ∠ H 1 H 2 M 1 . Опираясь на равенство треугольников, мы можем говорить о равенстве их сторон, т.е.: | М 1 Н 1 | = | М 2 Н 2 | . Теорема доказана.

Отметим, что расстояние между двумя параллельными прямыми – наименьшее из расстояний от точек одной прямой до точек другой.

Видео:✓ Расстояние между скрещивающимися прямыми | ЕГЭ-2018. Задание 13. Математика | Борис ТрушинСкачать

Нахождение расстояния между параллельными прямыми

Мы уже выяснили, что, по сути, чтобы найти расстояние между двумя параллельными прямыми, необходимо определить длину перпендикуляра, опущенного из некой точки одной прямой на другую. Способов, как это сделать, несколько. В каких-то задачах удобно воспользоваться теоремой Пифагора; другие предполагают использование признаков равенства или подобия треугольников и т.п. В случаях, когда прямые заданы в прямоугольной системе координат, возможно вычислить расстояние между двумя параллельными прямыми, используя метод координат. Рассмотрим его подробнее.

Зададим условия. Допустим, зафиксирована прямоугольная система координат, в которой заданы две параллельные прямые a и b . Необходимо определить расстояние между заданными прямыми.

Решение задачи построим на определении расстояния между параллельными прямыми: для нахождения расстояния между двумя заданными параллельными прямыми необходимо:

— найти координаты некоторой точки М 1 , принадлежащей одной из заданных прямых;

— произвести вычисление расстояния от точки М 1 до заданной прямой, которой эта точка не принадлежит.

Опираясь на навыки работы с уравнениями прямой на плоскости или в пространстве, определить координаты точки М 1 просто. При нахождении расстояния от точки М 1 до прямой пригодится материал статьи о нахождении расстояния от точки до прямой.

Вернемся к примеру. Пусть прямая a описывается общим уравнением A x + B y + C 1 = 0 , а прямая b – уравнением A x + B y + C 2 = 0 . Тогда расстояние между двумя заданными параллельными прямыми возможно вычислить, используя формулу:

M 1 H 1 = C 2 — C 1 A 2 + B 2

Выведем эту формулу.

Используем некоторую точку М 1 ( x 1 , y 1 ) , принадлежащую прямой a . В таком случае координаты точки М 1 будут удовлетворять уравнению A x 1 + B y 1 + C 1 = 0 . Таким образом, справедливым является равенство: A x 1 + B y 1 + C 1 = 0 ; из него получим: A x 1 + B y 1 = — C 1 .

Когда С 2 0 , нормальное уравнение прямой b будет иметь вид:

A A 2 + B 2 x + B A 2 + B 2 y + C 2 A 2 + B 2 = 0

При С 2 ≥ 0 нормальное уравнение прямой b будет выглядеть так:

A A 2 + B 2 x + B A 2 + B 2 y — C 2 A 2 + B 2 = 0

И тогда для случаев, когда С 2 0 , применима формула: M 1 H 1 = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2 .

А для С 2 ≥ 0 искомое расстояние определяется по формуле M 1 H 1 = — A A 2 + B 2 x 1 — B A 2 + B 2 y 1 — C 2 A 2 + B 2 = = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2

Таким образом, при любом значении числа С 2 длина отрезка | М 1 Н 1 | (от точки М 1 до прямой b ) вычисляется по формуле: M 1 H 1 = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2

Выше мы получили: A x 1 + B y 1 = — C 1 , тогда можем преобразовать формулу: M 1 H 1 = — C 1 A 2 + B 2 + C 2 A 2 + B 2 = C 2 — C 1 A 2 + B 2 . Так мы, собственно, получили формулу, указанную в алгоритме метода координат.

Разберем теорию на примерах.

Заданы две параллельные прямые y = 2 3 x — 1 и x = 4 + 3 · λ y = — 5 + 2 · λ . Необходимо определить расстояние между ними.

Решение

Исходные параметрические уравнения дают возможность задать координаты точки, через которую проходит прямая, описываемая параметрическими уравнениями. Таким образом, получаем точку М 1 ( 4 , — 5 ) . Требуемое расстояние – это расстояние между точкой М 1 ( 4 , — 5 ) до прямой y = 2 3 x — 1 , произведем его вычисление.

Заданное уравнение прямой с угловым коэффициентом y = 2 3 x — 1 преобразуем в нормальное уравнение прямой. С этой целью сначала осуществим переход к общему уравнению прямой:

y = 2 3 x — 1 ⇔ 2 3 x — y — 1 = 0 ⇔ 2 x — 3 y — 3 = 0

Вычислим нормирующий множитель: 1 2 2 + ( — 3 ) 2 = 1 13 . Умножим на него обе части последнего уравнения и, наконец, получим возможность записать нормальное уравнение прямой: 1 13 · 2 x — 3 y — 3 = 1 13 · 0 ⇔ 2 13 x — 3 13 y — 3 13 = 0 .

При x = 4 , а y = — 5 вычислим искомое расстояние как модуль значения крайнего равенства:

2 13 · 4 — 3 13 · — 5 — 3 13 = 20 13

Ответ: 20 13 .

В фиксированной прямоугольной системе координат O x y заданы две параллельные прямые, определяемые уравнениями x — 3 = 0 и x + 5 0 = y — 1 1 . Необходимо найти расстояние между заданными параллельными прямыми.

Решение

Условиями задачи определено одно общее уравнение, задаваемое одну из исходных прямых: x-3=0. Преобразуем исходное каноническое уравнение в общее: x + 5 0 = y — 1 1 ⇔ x + 5 = 0 . При переменной x коэффициенты в обоих уравнениях равны (также равны и при y – нулю), а потому имеем возможность применить формулу для нахождения расстояния между параллельными прямыми:

M 1 H 1 = C 2 — C 1 A 2 + B 2 = 5 — ( — 3 ) 1 2 + 0 2 = 8

Ответ: 8 .

Напоследок рассмотрим задачу на нахождение расстояния между двумя параллельными прямыми в трехмерном пространстве.

В прямоугольной системе координат O x y z заданы две параллельные прямые, описываемые каноническими уравнениями прямой в пространстве: x — 3 1 = y — 1 = z + 2 4 и x + 5 1 = y — 1 — 1 = z — 2 4 . Необходимо найти расстояние между этими прямыми.

Решение

Из уравнения x — 3 1 = y — 1 = z + 2 4 легко определются координаты точки, через которую проходит прямая, описываемая этим уравнением: М 1 ( 3 , 0 , — 2 ) . Произведем вычисление расстояния | М 1 Н 1 | от точки М 1 до прямой x + 5 1 = y — 1 — 1 = z — 2 4 .

Прямая x + 5 1 = y — 1 — 1 = z — 2 4 проходит через точку М 2 ( — 5 , 1 , 2 ) . Запишем направляющий вектор прямой x + 5 1 = y — 1 — 1 = z — 2 4 как b → с координатами ( 1 , — 1 , 4 ) . Определим координаты вектора M 2 M → :

M 2 M 1 → = 3 — ( — 5 , 0 — 1 , — 2 — 2 ) ⇔ M 2 M 1 → = 8 , — 1 , — 4

Вычислим векторное произведение векторов :

b → × M 2 M 1 → = i → j → k → 1 — 1 4 8 — 1 — 4 = 8 · i → + 36 · j → + 7 · k → ⇒ b → × M 2 M 1 → = ( 8 , 36 , 7 )

Применим формулу расчета расстояния от точки до прямой в пространстве:

M 1 H 1 = b → × M 2 M 1 → b → = 8 2 + 36 2 + 7 2 1 2 + ( — 1 ) 2 + 4 2 = 1409 3 2

Видео:Видеоурок "Угол между прямыми"Скачать

Расстояние между 2 прямыми в пространстве

Вы будете перенаправлены на Автор24

Очень часто на практике необходимо найти расстояние между точкой и некой прямой линией или между двумя прямыми линиями в пространстве, например, иногда определять расстояние между двумя линиями приходится и в реальной жизни. Хорошая иллюстрация такого примера — это знак, который вешают на мосты для грузовиков, указывающий максимальную высоту грузовика, которая может проехать под данным мостом.

Расстояние от верхней грани грузовика и нижней грани в данном случае определяют как расстояние между двумя прямыми.

Расстояние между 2 прямыми в пространстве — это отрезок, соединяющий две прямые линии по наикратчайшему расстоянию между ними, то есть перпендикулярный к обеим прямым.

Расстояние между двумя скрещивающимися прямыми в пространстве — это расстояние между одной заданной прямой и плоскостью, в которой лежит вторая прямая.

Чтобы было чуть проще понять, что это такое, давайте повторим определение скрещивающихся прямых:

Скрещивающиеся прямые — это две прямые, которые не лежат в одной плоскости и не имеют каких-либо совместных друг для друга точек.

Соответственно, для того чтобы найти расстояние между скрещивающимися прямыми в пространстве, необходимо от одной из прямых опустить перпендикуляр на плоскость, в которой лежит другая прямая.

Расстояние же между двумя параллельными прямыми в пространстве является одинаковым на протяжении всей длины параллельных прямых, то есть перпендикуляр, опущенный из одной параллельной прямой на другую, всегда будет одной и той же длины вне зависимости от того, из какой именно точки его опустили.

Видео:Расстояние между скрещивающимися прямымиСкачать

Метод координат для определения расстояния между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми в пространстве можно найти используя метод координат, для этого необходимо:

Готовые работы на аналогичную тему

1. Найти координаты точек $M_1$ и $M_2$, лежащих на прямых $a$ и $b$ соответственно.
2. Вычислить икс, игрек и зет направляющих векторов для прямых $a$ и $b$.
3. С помощью векторного произведения векторов $overline$ и $overline$ нужно найти вектор-нормаль для плоскости, в которой лежит прямая $b$. Затем необходимо записать общее уравнение плоскости: $A (x – x_0) + B(y – y_0) + C(z – z_0) = 0$, и от него перейти к нормированному виду уравнения плоскости следующего вида: $ x cdot cos α + y cdot cos β + z cdot cos – p = 0$, где $cos α, cos β$ и $cos γ$ — координаты единичного нормального вектора плоскости, а $p$ — свободный член, это число равно расстоянию от точки начала координат до плоскости.
4. Для вычисления расстояния от точки $M$ до искомой плоскости, нужно воспользоваться следующим уравнением: $M_1H_1 = |x_1 cdot cos α + y_1 cdot cos β + z_1 cdot cos – p|$, где $x_1, y_1, z_1$ – координаты точки $M_1$, лежащей на прямой $a$, а $H_1$ — точка, лежащая на искомой плоскости.

Найти расстояние между двумя скрещивающимися прямыми, заданными уравнениями: $d_1$: $frac = frac = frac$

Рисунок 1. Расстояние между двумя скрещивающимися прямыми в пространстве

Для этого воспользуемся следующей формулой:

Сначала найдём смешанное произведение векторов. Для этого найдём точки, лежащие на данных прямых, и их направляющие вектора:

$d_1$: $frac = frac = frac$, точка, лежащая на прямой — $M_1$ с координатами $(2;-1;0)$, а направляющий вектор — $overline

$ с координатами $(2; -3; -1)$

$d_2$: $begin frac = frac \ z – 1 = 0 end$, точка, лежающая на прямой — $M_2$ с координатами $(-1; 0; 1)$,

а её направляющий вектор — $overline

$ с координатами $(1; -2; 0)$

Теперь найдём вектор $overline$:

Найдём смешанное произведение векторов:

$overline

cdot overline

cdot overline = begin 2& 1 & -3 \ -3& -2 & 1 \ -1 & 0 & 1 \ end = — begin 1 & -3 \ -2 & 1 \ end + begin 2 & 1 \ -3 & -2 \ end = -(1 — 6) + (4 + 3) = 4$

Теперь найдём векторное произведение векторов:

$[|overline

× overline

|] = begin i& j & k \ 2 & -3 & -1 \ 1 & -2 & 0 end = begin -3 & -1 \ -2 & 0 end cdot overline — begin 2 & -1 \ 1 & 0 end cdot overline + begin 2 & -3 \ 1 & -2 end cdot overline$

$[|overline

× overline

|]= -2 overline — overline — overline$

Длина этого векторного произведения составит:

Соответственно, длина между скрещивающимися прямыми составит:

Даны две параллельные несовпадающие прямые $g$ и $m$, ниже приведены уравнения для них. Определить расстояние между ними.

Расстояние в этом случае для них вычисляется по следующей формуле:

$overline, overline$ — радиус-векторы для каждой прямой, а $s_1$ — направляющий вектор.

Радиус-вектор для первой прямой будет $r_1=$, а направляющий вектор $s_1 = $.

Радиус-вектор для второй прямой будет $r_2=$, а направляющий вектор $s_2 = $.

Найдём векторную разность радиус-векторов:

Теперь найдём её произведение с направляющим вектором для первой прямой:

$[overline — overline × overline] = begin i & j & k \ -2 & 0 & 0 \ 4 & 6 & 8 \ end = — 16j – 12k = $

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 09.01.2022

🎬 Видео

найти уравнения биссектрис углов между прямымиСкачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

21. Угол между прямой и плоскостьюСкачать

9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

14. Угол между прямыми в пространствеСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Задача C2: расстояние между двумя прямымиСкачать

Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать