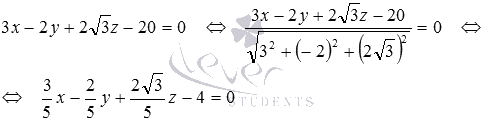Как найти расстояние между двумя параллельными плоскостями заданными уравнениями

Видео:Расстояние между параллельными плоскостямиСкачать

Формула для вычисления расстояния между плоскостями

Если заданы уравнения параллельных плоскостей A x + B y + C z + D₁ = 0 и A x + B y + C z + D₂ = 0, то расстояние между плоскостями можно найти, используя следующую формулу

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Примеры задач на вычисление расстояния между плоскостями

Решение. Проверим, параллельны ли плоскости, для этого умножим уравнение второй плоскости на 2

2 x + 4 y — 4 z + 18 = 0

Так как коэффициенты при неизвестных величинах у полученного уравнения и первого уравнения равны, то для вычисления расстояния между плоскостями можно использовати приведенную выше формулу:

Ответ: расстояние между плоскостями равно 4.

Видео:Расстояние между параллельными прямымиСкачать

Расстояние между двумя параллельными плоскостями – определение и примеры нахождения.

В этой статье содержится ответ на вопрос: «Как найти расстояние между двумя параллельными плоскостями методом координат»? Сначала дано определение расстояния между параллельными плоскостями. Далее получена формула, позволяющая вычислять расстояние между параллельными плоскостями, которые заданы в прямоугольной системе координат. В заключении разобраны решения примеров и задач на нахождение расстояния между параллельными плоскостями.

Навигация по странице.

Видео:Видеоурок "Расстояние между прямыми в пространстве"Скачать

Расстояние между двумя параллельными плоскостями – определение.

Расстояние между двумя параллельными плоскостями определяется через расстояние от точки до плоскости. Покажем, как это делается.

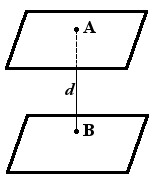
Рассмотрим две параллельные плоскости и . Возьмем на любой из этих плоскостей точку М₁ и опустим перпендикуляр М₁H₁ из этой точки на другую плоскость. Длина перпендикуляра M₁H₁ является расстоянием между параллельными плоскостями и .

Расстояние между параллельными плоскостями – это расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.

Такое определение расстояния между параллельными плоскостями не случайно. Оно тесно связано со следующей теоремой.

Все точки одной из параллельных плоскостей находятся на одинаковом расстоянии от другой плоскости.

Пусть нам даны две параллельные плоскости и . Чтобы доказать эту теорему нам нужно доказать, что два перпендикуляра М₁H₁ и M₂H₂ , проведенные из различных точек М₁ и М₂ одной из заданных параллельных плоскостей к другой плоскости, имеют одинаковую длину.

Прямые М₁H₁ и M₂H₂ параллельны, так как они перпендикулярны к одной плоскости. Из аксиомы о единственной плоскости, проходящей через три различные точки, не лежащие на одной прямой, следует, что через две параллельные прямые проходит единственная плоскость (об этом мы упоминали в разделе способы задания плоскости). Тогда будем считать, что через параллельные прямые M₁H₁ и M₂H₂ проходит плоскость . Очевидно, плоскость пересекает плоскости и по прямым М₁М₂ и H₁H₂ . Эти прямые не пересекаются (в противном случае плоскости и имели бы общую точку, что невозможно, так как они параллельны по условию), значит, они параллельны. Таким образом, в четырехугольнике М₁М₂H₂H₁ противоположные стороны попарно параллельны, следовательно, М₁М₂H₂H₁ — параллелограмм (в нашем случае прямоугольник). Следовательно, его противоположные стороны равны. То есть, , что и требовалось доказать.

Следует отметить, что расстояние между параллельными плоскостями является наименьшим из расстояний между произвольными точками этих параллельных плоскостей.

Видео:Определение расстояние между параллельными прямыми (Способ замены плоскостей проекции).Скачать

Нахождение расстояния между параллельными плоскостями – теория, примеры, решения.

Переходим к вопросу нахождения расстояния между параллельными плоскостями.

На уроках геометрии в 10-11 классах расстояние между параллельными плоскостями находится примерно так: строится какой-нибудь перпендикуляр от некоторой точки одной плоскости к другой плоскости и определяется его длина. Для этого, в зависимости от условий задачи, применяется либо теорема Пифагора, либо признаки равенства или подобия соответствующих треугольников, либо определения синуса, косинуса, тангенса угла.

Если же есть возможность ввести прямоугольную систему координат и заданные параллельные плоскости описать с помощью уравнений, то расстояние между параллельными плоскостями можно отыскать методом координат. Давайте детально его разберем.

Сформулируем условие задачи.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz и заданы две параллельные плоскости и . Требуется найти расстояние между этими параллельными плоскостями.

Решение будем строить на основе определения расстояния между параллельными плоскостями.

Так как в условии задачи определены плоскости и , то мы можем отыскать координаты некоторой точки М₁ , лежащей на одной из заданных плоскостей (для определенности будем считать, что точка лежит в плоскости ). Также мы можем получить нормальное уравнение плоскости в виде . Тогда искомое расстояние между параллельными плоскостями равно расстоянию от точки до плоскости , которой соответствует нормальное уравнение вида . Это расстояние вычисляется по формуле (ее вывод смотрите в разделе вычисление расстояния от точки до плоскости).

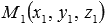
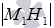
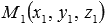
Итак, чтобы найти расстояние между двумя параллельными плоскостями нужно:

• определить координаты точки М₁ , лежащей в одной из заданных плоскостей;
• найти нормальное уравнение другой плоскости в виде ;
• вычислить искомое расстояние по формуле .

В частности, если в прямоугольной системе координат Oxyz плоскости соответствует общее уравнение плоскости , а плоскости — общее уравнение плоскости вида , то расстояние между параллельными плоскостями и вычисляется по формуле .

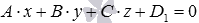
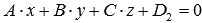
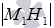
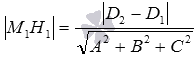
Поясним, как была получена эта формула.

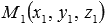
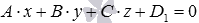
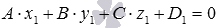
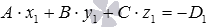
Пусть точка лежит в плоскости . Тогда координаты точки М₁ удовлетворяют уравнению плоскости , то есть, справедливо равенство , откуда имеем . Это равенство мы используем позже.

Нормальное уравнение плоскости в зависимости от знака числа D₂ имеет вид или . Но при любом значении числа D₂ расстояние от точки до плоскости можно вычислить по формуле . Учитывая полученное выше равенство , последняя формула примет вид .

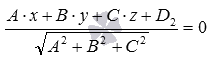
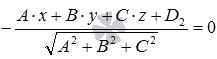
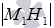
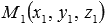
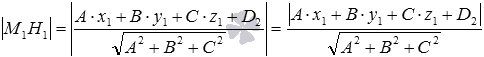
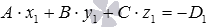
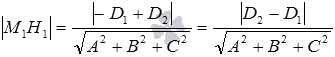
Осталось разобрать решения нескольких примеров.

Найдите расстояние между параллельными плоскостями и , которые в прямоугольной системе координат Oxyz определены уравнениями и соответственно.

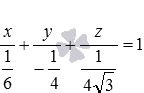
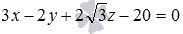
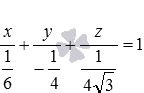
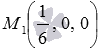
Заданное уравнение плоскости в отрезках вида позволяет легко найти координаты точки М₁ , лежащей в этой плоскости. В качестве точки М₁ возьмем точку, в которой плоскость пересекает ось Ox , то есть, .

Приведем общее уравнение плоскости к нормальному виду:

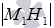
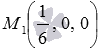
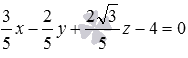
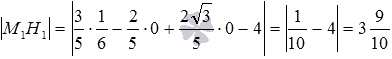
Теперь вычисляем расстояние от точки до плоскости :
.

Это и есть искомое расстояние между заданными параллельными плоскостями.

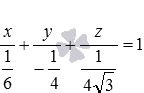
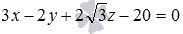
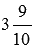
От уравнения плоскости в отрезках перейдем к общему уравнению плоскости: . Чтобы коэффициенты при переменных x , y и z в общих уравнениях плоскостей и стали равными, умножим обе части второго уравнения на два: . Теперь мы можем воспользоваться формулой для вычисления расстояния между параллельными плоскостями: .

.

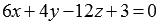
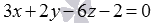
Вычислите расстояние между параллельными плоскостями и .

Очевидно, при таком условии задачи удобно использовать второй способ для нахождения расстояния между параллельными плоскостями. Если умножить обе части второго уравнения плоскости на два, то коэффициенты при переменных x , y и z в уравнениях 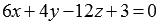и станут равны и можно будет применить формулу: .

Несомненно, можно было использовать первый способ.

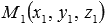
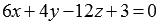
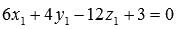
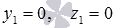
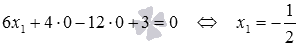
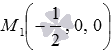
Пусть точка лежит в плоскости , тогда ее координаты удовлетворяют уравнению плоскости, то есть, справедливо равенство . Приняв , вычислим x₁ : . Следовательно, .

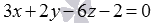
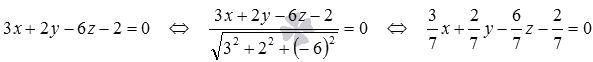
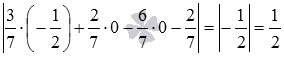
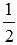
Теперь приведем общее уравнение плоскости к нормальному виду: . Тогда искомое расстояние между параллельными плоскостями равно .

.

Видео:9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать

Расстояние между двумя параллельными плоскостями: определение и примеры нахождения

Материал данной статьи позволяет получить навык определения расстояния между двумя параллельными плоскостями при помощи метода координат. Дадим определение расстояния между параллельными плоскостями, получим формулу для его расчета и рассмотрим теорию на практических примерах.

Видео:Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Расстояние между двумя параллельными плоскостями: определение

Расстояние между параллельными плоскостями – это расстояние от произвольной точки одной из рассматриваемых параллельных плоскостей до другой плоскости.

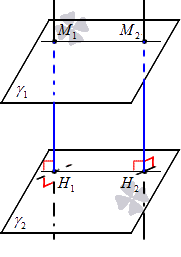
Пусть заданы две параллельные плоскости ϒ 1 и ϒ 2 . Из произвольной точки М 1 плоскости ϒ 1 опустим перпендикуляр М 1 Н 1 на другую плоскость ϒ 2 . Длина перпендикуляра М 1 Н 1 и будет являться расстоянием между заданными плоскостями.

Указанное определение расстояния между параллельными плоскостями имеет взаимосвязь со следующей теоремой.

Если две плоскости параллельны, то все точки одной из параллельных плоскостей находятся на одном и том же расстоянии от другой плоскости.

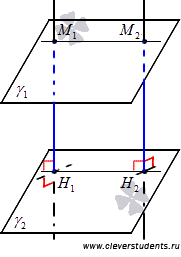
Допустим, заданы две параллельные плоскости ϒ 1 и ϒ 2 . Для получения доказательства теоремы необходимо доказать, что перпендикуляры, опущенные из различных произвольных точек одной плоскости к другой плоскости, равны. Пусть будут заданы некоторые произвольные точки М 1 и М 2 на плоскости ϒ 1 , и из них опущены перпендикуляры М 1 Н 1 и М 2 Н 2 на плоскость ϒ 2 . Таким образом, нам предстоит доказать, что М 1 Н 1 = М 2 Н 2 .

Прямые М 1 Н 1 и М 2 Н 2 параллельны, поскольку перпендикулярны одной плоскости. Опираясь на аксиому о единственной плоскости, проходящей через три различные точки, не лежащие на одной прямой, можем утверждать, что через две параллельные прямые проходит единственная плоскость. Будем считать, что существует некоторая плоскость ϒ 3 , проходящая через две параллельные прямые М 1 Н 1 и М 2 Н 2 . Очевидным фактом является то, что плоскость ϒ 3 пересекает плоскости ϒ 1 и ϒ 2 по прямым М 1 M 2 и Н 1 Н 2 , которые не пересекаются, а значит – параллельны (в ином случае, заданные плоскости имели бы общую точку, что невозможно в силу их параллельности по условию задачи). Таким образом, мы наблюдаем четырехугольник М 1 М 2 Н 1 Н 2 , у которого противоположные стороны являются попарно параллельными, т.е. М 1 М 2 Н 1 Н 2 – параллелограмм (в рассматриваемом случае – прямоугольник). Следовательно, противоположные стороны у этого параллелограмма равны, а значит | М 1 Н 1 | = | М 2 Н 2 | . Что и требовалось доказать.

Заметим также, что расстояние между параллельными плоскостями – наименьшее из расстояний между произвольными точками этих плоскостей.

Видео:7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

Нахождение расстояния между параллельными плоскостями

По программе 10 — 11 классов расстояние между параллельными плоскостями определяется построением перпендикуляра из любой точки одной плоскости, опущенного к другой плоскости; после чего находится длина этого перпендикуляра (при помощи теоремы Пифагора, признаков равенства, или подобия треугольников, или определения синуса, косинуса, тангенса угла).

В случае, когда уже задана или есть возможность задать прямоугольную систему координат, то мы имеем возможность определить расстояние между параллельными плоскостями при помощи метода координат.

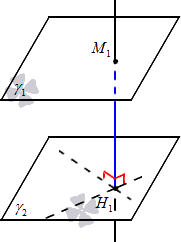
Пусть задано трехмерное пространство, а в нем — прямоугольная система координат и две параллельные плоскости ϒ 1 и ϒ 2 . Найдем расстояние между этими плоскостями, опираясь, в том числе, на определение расстояния между плоскостями, данное выше.

В исходных данных — плоскости ϒ 1 и ϒ 2 , и мы можем определить координаты ( x 1 , y 1 , z 1 ) некой точки M 1 , принадлежащей одной из заданных плоскостей: пусть это будет плоскость ϒ 1 . Также получим нормальное уравнение плоскости ϒ 2 : cos α · x + cos β · y + cos λ · z — p = 0 . В таком случае, искомое расстояние | М 1 Н 1 | будет равно расстоянию от точки М 1 ( x 1 , y 1 , z 1 ) до плоскости ϒ 2 (ей соответствует нормальное уравнение cos α · x + cos β · y + cos γ · z — p = 0 ). Тогда нужное расстояние вычислим по формуле: M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p . Вывод данной формулы можно изучить в теме вычисления расстояния от точки до плоскости.

Резюмируем. Для того,чтобы определить расстояние между двумя параллельными плоскостями, необходимо:

— найти координаты ( x 1 , y 1 , z 1 ) некой точки М 1 , принадлежащей одной из исходных плоскостей;

— определить нормальное уравнение другой плоскости в виде cos α · x + cos β · y + cos γ · z — p = 0 ;

— произвести расчет требуемого расстояние, используя формулу: M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p .

Если в прямоугольной системе координат плоскость ϒ 1 задается общим уравнением плоскости A · x + B · y + C · z + D 1 = 0 , а плоскость ϒ 2 – общим уравнением A · x + B · y + C · z + D 2 = 0 , тогда расстояние между параллельными плоскостями необходимо вычислять по формуле:

M 1 H 1 = D 2 — D 1 A 2 + B 2 + C 2

Покажем, как данная формула получена.

Пусть точка М 1 ( x 1 , y 1 , z 1 ) принадлежит плоскости ϒ 1 . В таком случае координаты этой точки будут отвечать уравнению плоскости A · x + B · y + C · z + D 1 = 0 , или верным будет равенство: A · x 1 + B · y 1 + C · z 1 + D 1 = 0 . Отсюда получим: A · x 1 + B · y 1 + C · z 1 + D 1 = 0 . Полученное равенство нам еще пригодится.

Плоскость ϒ 2 будет описываться нормальным уравнением плоскости A · x + B · y + C · z + D 2 A 2 + B 2 + C 2 = 0 или — A · x + B · y + C · z + D 2 A 2 + B 2 + C 2 = 0 (в зависимости от знака числа D 2 ). Однако при любом значение D 2 расстояние | М 1 Н 1 | возможно рассчитать, используя формулу:

M 1 H 1 = A · x 1 + B · y 1 + C · z 1 + D 2 A 2 + B 2 + C 2 = A · x 1 + B · y 1 + C · z 1 + D 2 A 2 + B 2 + C 2

Теперь задействуем полученное ранее равенство A · x 1 + B · y 1 + C · z 1 = — D 1 и преобразуем формулу:

M 1 H 1 = — D 1 + D 2 A 2 + B 2 + C 2 = D 2 — D 1 A 2 + B 2 + C 2

Даны две параллельные плоскости ϒ 1 и ϒ 2 , описываемые уравнениями x 1 6 + y — 1 4 + z 1 4 3 = 1 и 3 x — 2 y + 2 3 z — 20 = 0 соответственно. Необходимо определить расстояние между заданными плоскостями.

Решение

Решим задачу двумя способами.

1. Уравнение плоскости в отрезках, которое задано в условии задачи, дает возможность определить координаты точки М 1 , принадлежащей плоскости, описываемой этим уравнением. Как точку М 1 используем точку пересечения плоскости ϒ 1 и оси O x . Таким образом, имеем: M 1 1 6 , 0 , 0 .

Преобразуем общее уравнение плоскости ϒ 2 в нормальный вид:

3 x — 2 y + 2 3 z — 20 = 0 ⇔ 3 x — 2 y + 2 3 z — 20 3 2 + ( — 2 ) 2 + 2 3 2 = 0 ⇔ ⇔ 3 5 x — 2 5 y + 2 3 5 z — 4 = 0

Вычислим расстояние | М 1 Н 1 | от точки M 1 1 6 , 0 , 0 до плоскости 3 5 x — 2 5 y + 2 3 5 z — 4 = 0 :

M 1 H 1 = 3 5 · 1 6 — 2 5 · 0 + 2 3 5 · 0 — 4 = 1 10 — 4 = 3 9 10

Так мы получили искомое расстояние между исходными параллельными плоскостями.

1. Преобразуем уравнение плоскости в отрезках в общее уравнение плоскости:

x 1 6 + y — 1 4 + z 1 4 3 = 1 ⇔ 6 x — 4 y + 4 3 z — 1 = 0

Приравняем коэффициенты при переменных x , y , z в общих уравнениях плоскостей; с этой целью умножим обе части крайнего равенства на 2 :

3 x — 2 y + 2 3 z — 20 = 0 ⇔ 6 x — 4 y + 4 3 z — 40 = 0

Воспользуемся формулой для нахождения расстояния между параллельными плоскостями:

M 1 H 1 = D 2 — D 1 A 2 + B 2 + C 2 = — 40 — ( — 1 ) 6 2 + ( — 4 ) 2 + ( 4 3 ) 2 = 39 100 = 3 9 10 .

Ответ: 3 9 10 .

Даны две параллельные плоскости, описываемые уравнениями: 6 x + 4 y — 12 z + 3 = 0 и 3 x + 2 y — 6 z — 2 = 0 . Необходимо найти расстояние между этими плоскостями.

Решение

Удобнее будет использовать второй способ решения подобных задач. Умножим обе части второго уравнения на 2 , и коэффициенты в уравнениях плоскостей станут равны: 6 x + 4 y — 12 z + 3 = 0 и 6 x + 4 y — 12 z — 4 = 0 . Теперь можно использовать формулу:

M 1 H 1 = — 4 — 3 6 2 + 4 2 + ( — 12 ) 2 = 7 196 = 1 2

Однако попробуем найти ответ и первым способом: допустим, точка M 1 ( x 1 , y 1 , z 1 ) принадлежит плоскости 6 x + 4 y — 12 z + 3 = 0 . Соответственно, координаты этой точки отвечают уравнению плоскости, и верным будет равенство:

6 x 1 + 4 y 1 — 12 z 1 + 3 = 0

Пусть y 1 = 0 , z 1 = 0 , тогда x 1 : 6 x 1 + 4 · 0 — 12 · 0 + 3 = 0 ⇔ x 1 = — 1 2

Таким образом, точка получает точные координаты: M 1 — 1 2 , 0 , 0 .

Преобразуем общее уравнение плоскости 3 x + 2 y — 6 z — 2 = 0 в нормальный вид:

3 x + 2 y — 6 z — 2 = 0 ⇔ 3 x + 2 y — 6 z — 2 = 0 3 2 + 2 2 + — 6 = 0 ⇔ 3 7 x + 2 7 y — 6 7 z — 2 7 = 0

В таком случае, требуемое расстояние между плоскостями равно: 3 7 · — 1 2 + 2 7 · 0 — 6 7 · 0 — 6 7 · 0 — 2 7 = — 1 2 = 1 2

💥 Видео

14. Угол между прямыми в пространствеСкачать

7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

57. Определение расстояния между двумя параллельными прямымиСкачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Длина отрезкаСкачать

Задача C2: расстояние между двумя прямымиСкачать

Расстояние между скрещивающимися прямыми и уравнение их общего перпендикуляра.Скачать

Угол между прямыми в пространстве. 10 класс.Скачать

Найти угол между плоскостямиСкачать

✓ Расстояние между скрещивающимися прямыми | ЕГЭ-2018. Задание 13. Математика | Борис ТрушинСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать