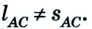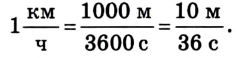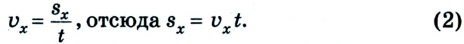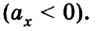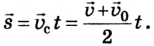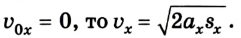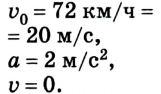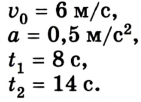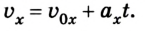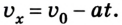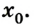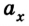Содержание:
Основная задача механики — описание движения тел, т. е. выяснение закона (уравнения) их движения. Как отмечал А. Эйнштейн, наиболее фундаментальная проблема, остававшаяся нерешенной на протяжении тысячелетий, — это проблема движения. Собственно, учение о движении стало наукой лишь со времен Галилео Галилея и Исаака Ньютона.
Кинематика, изучает конкретные механические та их взаимодействия с другими телами. Она фактически объединяет простейшие пространственно-временные зависимости, в частности изменение координат тела со временем (как функцию времени).
Поэтому кинематику часто называют геометрией движения.
Кинематика изучает механические движения тел без учета их взаимодействия с другими телами.
- Кинематика
- Механическое движение и траектория движения
- Путь и перемещение
- Равномерное прямолинейное движение
- Перемещение и путь при равноускоренном прямолинейном движении
- теория по физике 🧲 кинематика
- Перемещение при разгоне и торможении тела
- Этап торможения
- Этап разгона
- Перемещение в n-ную секунду прямолинейного равноускоренного движения
- Проекция и график перемещения
- График пути
- Механическое движение
- Механическое движение
- Прямолинейное равномерное движение
- Скалярные величины (определяются только значением)
- Векторные величины (определяются значением и направлением)
- Проецирование векторов
- Уравнение движения
- Прямолинейное равноускоренное движение
- Уравнение движения и формула конечной скорости
- Движение по вертикали
- 🔍 Видео
Видео:Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Кинематика
Физика изучает разнообразные явления и процессы, происходящие вокруг нас. Как вам известно, в зависимости от их природы различают механические, тепловые, электрические, магнитные, световые и другие физические явления. Раздел физики, который объясняет движение и взаимодействие тел, называется механикой.
Слово «механика» впервые ввел Аристотель. Оно означает «машина».
Механика — одна из древнейших наук. Ее возникновение и развитие связано с практическими потребностями человека. Первые труды по механике, в которых рассматривались свойства простых механизмов и машин, появились еще в Древней Греции. Весомый вклад в ее становление сделали такие корифеи науки, как Аристотель (IV в. до н. э.), Архимед (III в. до н. э.), Леонардо да Винчи (XV в.), Галилео Галилей (XVII в.) и др. В завершенном виде как классическая теория она получила обоснование в работе Исаака Ньютона «Математические начала натуральной философии» (1687 г.). Современная механика, в основе которой лежит теория относительности, создана в начале XX в. Альбертом Эйнштейном.
Основная задача механики состоит в том, чтобы на основании параметров движения тела: координат, пройденного пути, перемещения, угла поворота, скорости, силы и т. д. — найти закон или уравнение, которое описывает это движение.
Основная задача механики состоит в том, чтобы найти уравнение движения тела с помощью параметров, описывающих это движение.
Т. е. если мы при помощи этих физических величин сможем установить положение тела в любой момент времени, то основная задача механики считается решенной. В зависимости от способов ее решения в механике выделяют три раздела: кинематика, динамика и статика.
Кинематика изучает, как движется тело, не вникая в причины, вызывающие именно такое движение. Поэтому кинематические уравнения состоят лишь из пространственных характеристик механического движения: пройденного пути, изменения координат тела, скорости и т. д. В них нет сил, изменяющих это движение.
В переводе с греческого слово кинематика» (kinematos) означает движение.
Механическое движение и траектория движения
Чаще всего в обыденной жизни мы наблюдаем явление, которое называется механическим движением. Например, автомобиль едет по дороге, в небе «плывут» тучи, ребенок катается на качелях, Луна вращается вокруг Земли и т. д. Во всех этих случаях происходит изменение положения одного тела или его частей относительно других. Чтобы убедиться в этом, необходимо выбрать тело отсчета, относительно которого можно фиксировать положение движущегося тела в любой момент времени. Тело отсчета выбирают произвольно. В приведенных примерах это может быть столб или дерево возле дороги, дом, поверхность Земли и т. д.
Для того чтобы описать движение тела, необходимо точно знать его местоположение в пространстве в произвольный момент времени, т. е. уметь определять изменение положения тела в пространстве относительно других тел с течением времени. Как известно, легче всего это можно сделать с помощью системы координат. Например, зафиксировать «адрес» тела как определенное его положение в пространстве, измерив расстояния или углы в некоторой системе координат.
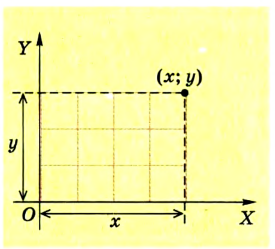
Например, в географии положение тела на земной поверхности задается двумя числами на пересечении меридиана и параллели, которые называются географической долготой и широтой. В математике «адрес» точки чаще всего определяют ее координатами, в частности в прямоугольной (декартовой) системе координат на плоскости — это расстояния х и у (рис. 1.1).
Взаимные изменения положения тела или его частей в пространстве с течением времени называются механическим движением.
Систему координат, как правило, связывают с телом отсчета. В данном случае движущееся тело характеризуется изменением положения в пространстве относительно тела отсчета, т. е. изменением его координат с течением времени.
Математически это можно записать в таком виде: х = x(t); у = y(t).
Для того чтобы определить такое изменение в любой момент времени, с телом отсчета и системой координат необходимо связать средство измерения времени, к примеру секундомер или хронометр. Тогда тело отсчета, связанную с ним систему координат и секундомер как единое целое называют системой отсчета.
Как известно, реальные физические тела имеют форму и объем. Поэтому однозначно задать их положение в пространстве не всегда представляется возможным, поскольку различные их части имеют разные координаты. Однако эту проблему можно упростить, если не брать во внимание размеры тела. Такое возможно лишь при определенных условиях.
Чтобы выяснить их, рассмотрим движение автомобиля. На значительных расстояниях, например на шоссе между Киевом и Харьковом, размерами автомобиля можно пренебречь, поскольку они значительно меньше расстояния между этими городами. Поэтому нет необходимости рассматривать особенности движения каждой части кузова автомобиля — достаточно его представить как движение точки.
Таким образом, для упрощения описания движения тел, когда их размерами при определенных условиях можно пренебречь, применяют понятие материальной точки. Это условное тело, не имеющее размеров, которое определяет положение реального тела в пространстве при помощи координат такой, материальной точки. Ее геометрический образ — невесомая точка, не имеющая размеров. В случае поступательного движения, при котором все точки тела движутся одинаково, любое тело можно считать материальной точкой.
Материальная точка — это физическая модель, при помощи которой представляют реальное тело, пренебрегая его размерами.
Часто кроме движущихся предметов мы наблюдаем тела, пребывающие в состоянии покоя. Однако абсолютно неподвижных тел в природе не существует.
Рассмотрим такой пример. В вагоне на столе стоит бутылка с водой (рис. 1.2). Во время движения поезда разные наблюдатели — пассажир в купе и провожающий на перроне — оценят ее состояние движения по-разному. Для сидящего пассажира она неподвижна, поскольку расстояние от него до бутылки не изменяется. Для провожающего на перроне 16 она движется, потому что изменяет свое положение с течением времени в системе отсчета, связанной с перроном.
Следовательно, состояние покоя является относительным, равно как и состояние движения, поскольку зависит от выбранной системы отсчета. Поэтому в дальнейшем при рассмотрении движения тела мы в первую очередь будем определяться с выбором системы отсчета, потому что от этого нередко зависит сложность уравнений, описывающих данное движение. Правильный выбор системы отсчета ведет к упрощению уравнений движения.
Состояние покоя и состояние движения тела относительны, поскольку зависят от выбора системы отсчета.
Рассмотрим движущееся тело, последовательно фиксируя его положение в определенные моменты времени. Если теперь соединить все точки, в которых побывало тело во время своего движения, то получим мнимую линию, которая называется траекторией движения. Траектория движения может быть видимой (след от самолета на небосклоне, линия от карандаша или ручки при записи в тетради) и невидимой (полет птички, движение теннисного мяча и т. д.).
По форме траектории механическое движение бывает прямолинейным и криволинейным (рис. 1.3).
Положение броуновской частички через определенные промежутки времени.
Рис. 1.3. Различные формы траектории
Траектория прямолинейного движения — прямая линия. Например, падение тела с определенной высоты или движение шарика по наклонному желобу. Во время криволинейного движения тело перемещается по произвольной кривой. Часто реальное движение тел является комбинацией прямолинейного и криволинейного движений. Например, комбинированным есть движение автобуса по маршруту: на разных участках траектория его движения может быть и прямолинейной, и криволинейной.
Поскольку движение тел происходит в определенных системах отсчета, то и траектория рассматривается относительно них. Ведь она отображает во времени последовательные положения тела в некоторой системе отсчета. Поэтому она будет отличаться формой в различных системах отсчета, т. е. траектории движения также относительны. Например, все точки колеса велосипеда относительно его оси описывают окружность, однако в системе отсчета, связанной с землей, эта линия более сложная (рис. 1.4).
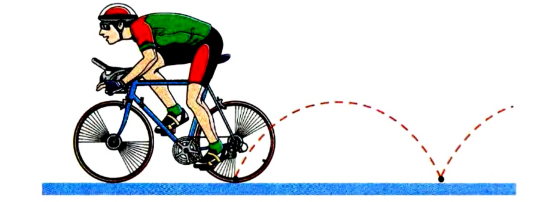
Рис. 1.4. Траектория движения точки обода колеса велосипеда
Путь и перемещение
Зная траекторию движения, можно определить путь, пройденный телом: для этого необходимо измерить длину траектории между начальной и конечной точками движения.
Путь — это длина траектории, которую проходит тело или материальная точка за определенный интервал времени. Он обозначается латинской буквой l. Данная физическая величина является скалярной и характеризуется лишь значением длины траектории движения.
В Международной системе единиц (СИ) путь измеряется в метрах (м). На практике используют также другие единицы пути — километр (км), сантиметр (см) и др.
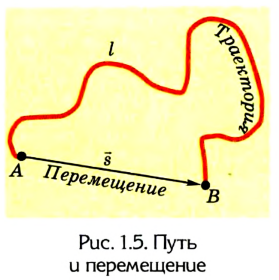
Часто, для того чтобы более полно охарактеризовать движение тела и найти его новое положение, кроме пройденного пути (длины траектории), необходимо указать также направление, в котором двигалось тело. Например, водителю автомобиля приходится ехать по извилистой дороге (рис. 1.5).
Пройденный путь — это длина дороги I, по которой ехал автомобиль. Водитель же совершил перемещение в пространстве из точки А в точку В, которое можно найти, соединив начальное и конечное положение тела прямой линией, указав при этом направление движения.
Следовательно, направленный отрезок прямой, соединяющий начальное положение движущегося тела с конечным, называется перемещением. Перемещение — это векторная величина. Оно обозначается латинской буквой 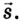
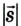
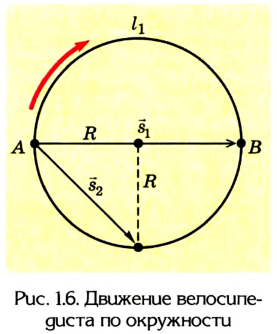
Путь и перемещение могут отличаться своими значениями. Чтобы убедиться в этом, рассмотрим движение велосипедиста по окружности радиуса R= 100 м (рис. 1.6).
Допустим велосипедист стартует в точке А. Проехав половину окружности, он окажется в точке В. Пройденный им путь равен дуге 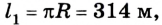
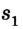
В момент времени, когда велосипедист проедет 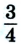
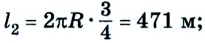
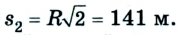
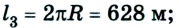
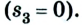
Путь и перемещение имеют также одинаковые значения, когда тело движется прямолинейно лишь в одном направлении.
В рассмотренном нами примере пройденный путь и перемещение разные, отличаются по своему значению. Возникает вопрос: могут ли они совпадать, быть одинаковыми? Можно легко убедиться в том, что такое возможно, если, во-первых, траектория движения будет прямой, во-вторых, движение происходит в одну сторону. Как подтверждение этого, рассмотрим — такой пример.
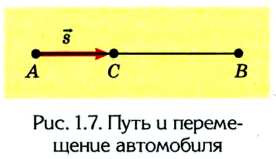
Допустим, что автомобиль движется прямолинейно по шоссе из пункта А в пункт В, а затем возвращается в пункт С. Расстояние между пунктами 2 км и 4 км соответственно, все они размещены на одной прямой (рис. 1.7).
Двигаясь из пункта А в пункт В, автомобиль проходит путь 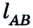
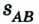
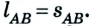
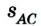
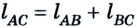
Следовательно, пройденный путь и перемещение по своему значению одинаковы лишь в том случае, если тело движется по прямой и не изменяет направление движения.
Равномерное прямолинейное движение
Простейшим видом механического движения является равномерное прямолинейное движение. Это такое движение, при котором тело, двигаясь по прямой, за любые одинаковые интервалы времени совершает одинаковые перемещения. Его траектория — прямая линия. Поэтому его можно описать переменой одной из координат, например х = x(t), если координатная ось совпадает с направлением движения.
Пусть тело в начальный момент движения имеет координату 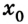
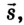
Как известно, в СИ скорость
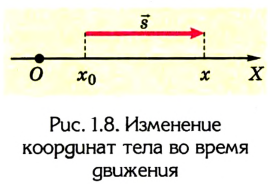
измеряется в метрах за секунду (м/с). 1 м/с — это скорость такого равномерного прямолинейного движения, при которой тело за 1 с совершает перемещение 1 м. На практике используют также другие единицы скорости, например километр в час:
Поскольку перемещение 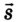
При равномерном движении значение скорости остается постоянным, поскольку за любые равные интервалы времени совершаются равные перемещения.
Как известно, основной задачей механики является определение положения тела в пространстве в произвольный момент времени. Следовательно, чтобы ее решить, надо найти координаты тела либо их изменение во времени: х — x(t). В механике такое уравнение называется уравнением движения. При решении задач с использованием уравнения движения векторные величины, характеризующие движение тела, записывают в проекциях на соответствующую ось. Следовательно, из формулы (1) получаем:
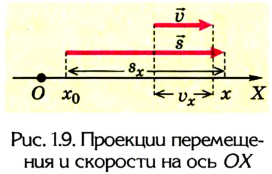
Из рисунков 1.8 и 1.9 понятно, что 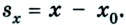
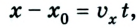

Уравнения равномерного прямолинейного движения:
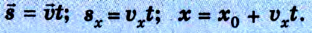
Рассмотрим теперь различные случаи равномерного прямолинейного движения (рис. 1.10).
Из рисунка следует, что если направление движения тела совпадает с направлением координатной оси, то 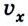
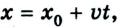
Если же направление движения тела противоположно направлению координатной оси, то 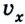
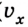
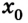
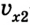
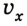
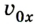
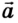
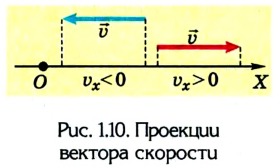
Если скорость тела со временем уменьшается 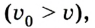
В данном случае в соответствии с выбранным направлением координатной оси ОХ проекция ускорения будет отрицательной
Вместе с тем знак проекции ускорения не определяет характер движения — оно ускоряющееся или замедляющееся, в зависимости от выбора системы отсчета. В этом легко убедиться, если рассмотреть случай, когда оба тела движутся в противоположных направлениях. Тогда одно из тел имеет положительную проекцию ускорения 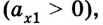
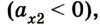
Из формул (1) и (2) можно получить кинематическое уравнение скорости для равноускоренного движения:

или в проекциях на ось ОХ:
Выведем теперь кинематическое уравнение перемещения для равноускоренного движения. Учтем, что скорость во время такого движения постоянно изменяется, например сначала она равна 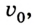
Подставив в данную формулу уравнение (3) и произведя некоторые преобразования, получим: 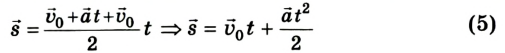
или в проекциях на ось ОХ: 
Если начальная скорость тела равна 0 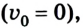

или в проекциях на ось ОХ: 
Для прямолинейного движения, учитывая, что 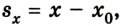
или для случая, когда 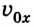

Следует помнить, что в ходе решения задач необходимо учитывать знаки проекций в соответствующих уравнениях.
При определении проекции перемещения не всегда известно время, в течение которого происходило движение. Тогда можно воспользоваться иным уравнением. Чтобы его получить, подставим в кинематическое уравнение 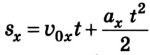
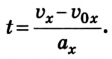

Отсюда 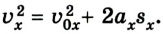
Задача №5
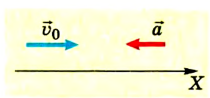
Водитель начинает тормозить в тот момент, когда спидометр автомобиля фиксирует скорость 72 км/ч. Через какое время автомобиль остановится, если он двигался с ускорением 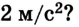
Дано:
По условию задачи спидометр показывает начальную скорость автомобиля 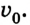
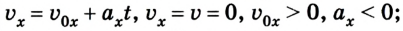
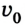
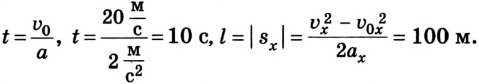
Ответ: автомобиль остановился через 10 с, проехав 100 м.
Задача №6
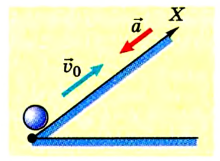
Шарик толкнули по наклонному желобу вверх со скоростью 6 м/с. Шарик движется с ускорением 0,5 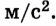
Дано:
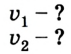
Решение
Направим ось ОХ вдоль желоба (см. рис.).
Учитывая знаки проекций скорости и ускорения, имеем
Отсюда уравнение для 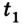
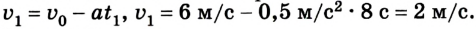
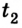
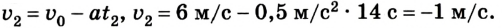
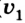
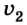
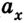
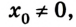
Если 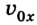
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Тема: Путь и перемещениеСкачать

Перемещение и путь при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.
При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:
Пример №1. По графику определить перемещение тела в момент времени t=3 с.
Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:
Извлекаем из графика необходимые данные:
- Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
- Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).
Подставляем известные данные в формулу:
Видео:Урок 12. Равномерное прямолинейное движениеСкачать

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещения
Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
В итоге получается формула:
Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v0 = 0), эта формула принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:
Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.
Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
Когда тело тормозит, через некоторое время t1оно останавливается. Поэтому скорость в момент времени t1 равна 0:
При торможении перемещение s1 равно:
Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
При разгоне перемещение s2 равно:
При этом модуль перемещения в течение всего времени движения равен:
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с 2 . Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:
Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
Подставляем выраженные величины в формулу:
Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:
За первую секунду тело переместится на расстояние, равное:
За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:
За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:
Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:
Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду
Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:
Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:
где t — время одного промежутка, а n — порядковый номер этого промежутка.
Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с 2 . Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:
Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:
График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:
Определение направления знака проекции ускорения по графику его перемещения:
- Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
- Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.
Пример №6. Определить ускорение тела по графику его перемещения.
Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:
Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:
График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.
В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:
- 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
- 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.
Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.
При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:
Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x ( t ) = x 0 + v 0 t + a t 2 2 . .
Теперь мы можем выделить кинематические характеристики движения тела:
Перемещение тела определяется формулой:
s = v 0 t + a t 2 2 . .
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x ( t ) = v 0 t + a t 2 2 . . = 5 t − 3 t 2
Кинетическая энергия тела определяется формулой:
Скорость при прямолинейном равноускоренном движении равна:
v = v 0 + a t = 5 − 6 t
Поэтому кинетическая энергия тела равна:
E k = m ( 5 − 6 t ) 2 2 . . = 0 , 2 2 . . ( 5 − 6 t ) 2 = 0 , 1 ( 5 − 6 t ) 2
Следовательно, правильная последовательность цифр в ответе будет: 34.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
pазбирался: Алиса Никитина | обсудить разбор | оценить
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Механическое движение
О чем эта статья:
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Перемещение — вектор, проведенный из начальной точки пути в конечную [м].
Видео:Решение графических задач на равномерное движениеСкачать

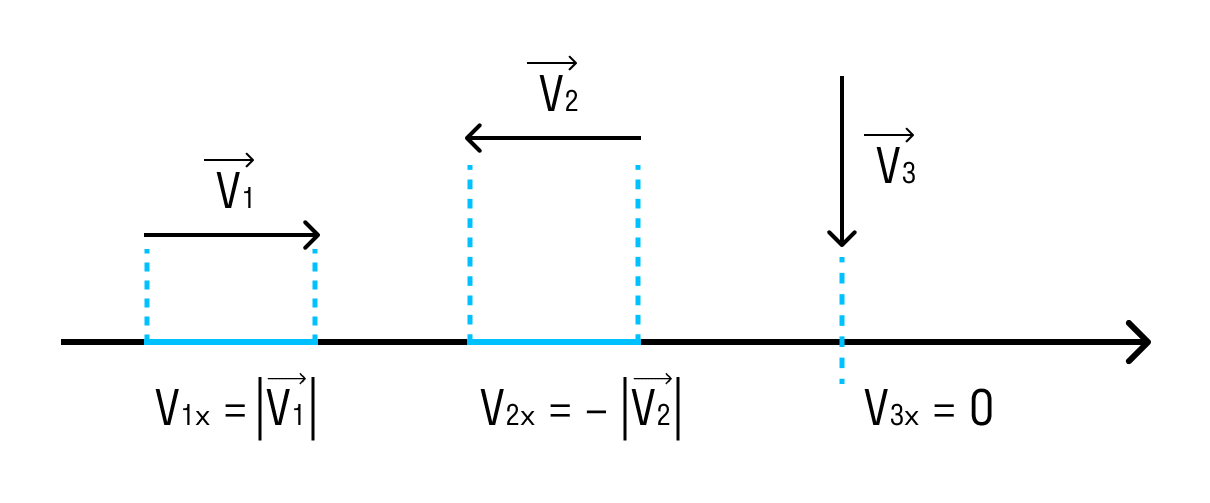
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
— скорость [м/с]
— перемещение [м]
— время [с]
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!
Видео:Физика - уравнения равноускоренного движенияСкачать

Уравнение движения
Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v