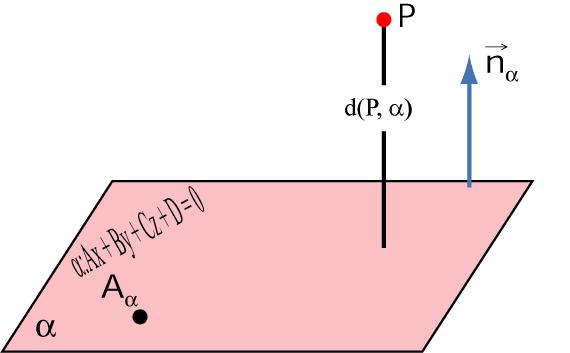
Данная статья рассматривает понятие проекции точки на прямую (ось). Мы дадим ему определение с использованием поясняющего рисунка; изучим способ определения координат проекции точки на прямую (на плоскости или в трехмерном пространстве); разберем примеры.
- Проекция точки на прямую, определение
- Нахождение координат проекции точки на прямую
- Проекция точки на прямую онлайн
- Предупреждение
- Проекция точки на прямую − теория, примеры и решения
- Как найти проекцию точки на плоскость: методика определения и пример решения задачи
- Уравнение для описания плоскости
- Понятие о проекции точки и ее вычисление
- Вычисление расстояния от плоскости до точки
- Пример задачи
- 🎦 Видео
Видео:Как найти проекцию точки на прямую. Линейная алгебраСкачать

Проекция точки на прямую, определение
В статье «Проекция точки на плоскость, координаты» мы упоминали, что проецирование фигуры является обобщенным понятием перпендикулярного или ортогонального проецирования.
Все геометрические фигуры состоят из точек, соответственно проекция этой фигуры есть множество проекций всех ее точек. Поэтому, чтобы иметь возможность спроецировать фигуру на прямую, необходимо получить навык проецирования точки на прямую.
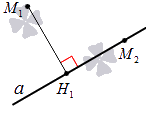
Проекция точки на прямую – это или сама точка, если она принадлежит заданной прямой, или основание перпендикуляра, опущенного из этой точки на заданную прямую.
Рассмотрим рисунок ниже: точка H 1 служит проекцией точки М 1 на прямую a , а точка М 2 , принадлежащая прямой, является проекцией сама себя.
Данное определение верно для случая на плоскости и в трехмерном пространстве.
Чтобы на плоскости получить проекцию точки М 1 на прямую a , проводится прямая b , проходящая через заданную точку M 1 и перпендикулярная прямой a . Таким образом, точка пересечения прямых a и b будет проекцией точки М 1 на прямую a .
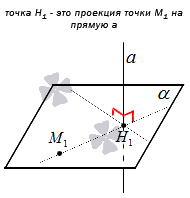
В трехмерном пространстве проекцией точки на прямую будет служить точка пересечения прямой a и плоскости α , проходящей через точку М 1 и перпендикулярной прямой a .
Видео:Прямая на плоскости. Проекция точки на прямуюСкачать

Нахождение координат проекции точки на прямую
Рассмотрим данный вопрос в случаях проецирования на плоскости и в трехмерном пространстве.
Пусть нам заданы прямоугольная система координат O x y , точка М 1 ( x 1 , y 1 ) и прямая a . Необходимо найти координаты проекции точки М 1 на прямую a .
Проложим через заданную точку М 1 ( x 1 , y 1 ) прямую b перпендикулярно прямой a . Точку пересечения маркируем как H 1 . Точка Н 1 будет являться точкой проекции точки М 1 на прямую a .
Из описанного построения можно сформулировать алгоритм, который позволяет находить координаты проекции точки М 1 ( x 1 , y 1 ) на прямую a :
— составляем уравнение прямой (если оно не задано). Для совершения этого действия необходим навык составления основных уравнений на плоскости;
— записываем уравнение прямой b (проходящей через точку М 1 и перпендикулярной прямой a ). Здесь поможет статья об уравнении прямой, проходящей через заданную точку перпендикулярно заданной прямой;
— определяем искомые координаты проекции как координаты точки пересечения прямых a и b . Для этого решаем систему уравнений, составляющие которой – уравнения прямых a и b .
На плоскости O x y заданы точки М 1 ( 1 , 0 ) и прямая a (общее уравнение – 3 x + y + 7 = 0 ). Необходимо определить координаты проекции точки М 1 на прямую a .
Решение
Уравнение заданной прямой известно, поэтому, согласно алгоритму, переходим к шагу записи уравнения прямой b . Прямая b перпендикулярна прямой a , а значит нормальный вектор прямой a служит направляющим вектором прямой b . Тогда направляющий вектор прямой b запишем как b → = ( 3 , 1 ) . Запишем и каноническое уравнение прямой b , поскольку нам также заданы координаты точки М 1 , через которую проходит прямая b :
Заключительным шагом определяем координаты точки пересечения прямых a и b . Перейдем от канонических уравнений прямой b к общему ее уравнению:
x — 1 3 = y 1 ⇔ 1 · ( x — 1 ) = 3 · y ⇔ x — 3 y — 1 = 0
Составим систему уравнений из общих уравнений прямых a и b и решим ее:
3 x + y + 7 = 0 x — 3 y — 1 = 0 ⇔ y = — 3 x — 7 x — 3 y — 1 = 0 ⇔ y = — 3 x — 7 x — 3 · ( — 3 x — 7 ) — 1 = 0 ⇔ ⇔ y = — 3 x — 7 x = — 2 ⇔ y = — 3 · ( — 2 ) — 7 x = — 2 ⇔ y = — 1 x = — 2
В конечном итоге мы получили координаты проекции точки М 1 ( 1 , 0 ) на прямую 3 x + y + 7 = 0 : ( — 2 , — 1 ) .
Ответ: ( — 2 , — 1 ) .
Подробнее рассмотрим случай, когда необходимо определить координаты проекции заданной точки на координатные прямые и параллельные им прямые.
Пусть заданы координатные прямые O x и O y , а также точка М 1 ( x 1 , y 1 ) . Понятно, что проекцией заданной точки на координатную прямую O x вида y = 0 будет точка с координатами ( x 1 , 0 ) . Так и проекция заданной точки на координатную прямую O y будет иметь координаты 0 , y 1 .
Любую произвольную прямую, параллельную оси абсцисс, возможно задать неполным общим уравнением B y + C = 0 ⇔ y = — C B , а прямую, параллельную оси ординат — A x + C = 0 ⇔ x = — C A.
Тогда проекциями точки М 1 ( x 1 , y 1 ) на прямые y = — C B и x = — C A станут точки с координатами x 1 , — C B и — C A , y 1 .
Определите координаты проекции точки М 1 ( 7 , — 5 ) на координатную прямую O y , а также на прямую, параллельную прямой O y 2 y — 3 = 0 .
Решение
Запишем координаты проекции заданной точки на прямую O y : ( 0 , — 5 ) .
Запишем уравнение прямой 2 y — 3 = 0 в виде y = 3 2 . Становится видно, что проекция заданной точки на прямую y = 3 2 будет иметь координаты 7 , 3 2 .
Ответ: ( 0 , — 5 ) и 7 , 3 2 .
Пусть в трехмерном пространстве заданы прямоугольная система координат O x y z , точка М 1 ( x 1 , y 1 , z 1 ) и прямая a . Найдем координаты проекции точки М 1 на прямую a .
Построим плоскость α , проходящую через точку М 1 и перпендикулярную прямой a . Проекцией заданной точки на прямую a станет точка пересечения прямой a и плоскости α . Исходя из этого, приведем алгоритм для нахождения координат проекции точки М 1 ( x 1 , y 1 , z 1 ) на прямую a :
— запишем уравнение прямой а (если оно не задано). Для решения этой задачи необходимо ознакомиться со статьей об уравнениях прямой в пространстве;
— составим уравнение плоскости α , проходящей через точку М 1 и перпендикулярной прямой a (см. статью «Уравнение плоскости, проходящей через заданную точку перпендикулярно заданной прямой»);
— найдем искомые координаты проекции точки М 1 ( x 1 , y 1 , z 1 ) на прямую a – это будут координаты точки пересечения прямой α и плоскости α (в помощь – статья «Координаты точки пересечения прямой и плоскости»).
Задана прямоугольная система координат O x y z , и в ней – точка М 1 ( 0 , 1 , — 1 ) и прямая a . Прямой a соответствуют канонические уравнения вида: x + 2 3 = y — 6 — 4 = z + 1 1 . Определите координаты проекции точки М 1 на прямую a .
Решение
Используем указанный выше алгоритм. Уравнения прямой a известны, поэтому первый шаг алгоритма пропускаем. Запишем уравнение плоскости α . Для этого определим координаты нормального вектора плоскости α . Из заданных канонических уравнений прямой a выделим координаты направляющего вектора этой прямой: ( 3 , — 4 , 1 ) , который будет являться нормальным вектором плоскости α , перпендикулярной прямой a . Тогда n → = ( 3 , — 4 , 1 ) – нормальный вектор плоскости α . Таким образом, уравнение плоскости α будет иметь вид:
3 · ( x — 0 ) — 4 · ( y — 1 ) + 1 · ( z — ( — 1 ) ) = 0 ⇔ 3 x — 4 y + z + 5 = 0
Теперь найдем координаты точки пересечения прямой а и плоскости α, для этого используем два способа:
- Заданные канонические уравнения позволяют получить уравнения двух пересекающихся плоскостей, определяющих прямую a :
x + 2 3 = y — 6 — 4 = z + 1 1 ⇔ — 4 · ( x + 2 ) = 3 · ( y — 6 ) 1 · ( x + 2 ) = 3 · ( z + 1 ) 1 · ( y — 6 ) = — 4 · ( z + 1 ) ⇔ 4 x + 3 y — 10 = 0 x — 3 z — 1 = 0
Чтобы найти точки пересечения прямой 4 x + 3 y — 10 = 0 x — 3 z — 1 = 0 и плоскости 3 x — 4 y + z + 5 = 0 , решим систему уравнений:
4 x + 3 y — 10 = 0 x — 3 z — 1 = 0 3 x — 4 y + z + 5 = 0 ⇔ 4 x + 3 y = 10 x — 3 z = 1 3 x — 4 y + z = — 5
В данном случае используем метод Крамера, но возможно применить любой удобный:
∆ = 4 3 0 1 0 — 3 3 — 4 1 = — 78 ∆ x = 10 3 0 1 0 — 3 — 5 — 4 1 = — 78 ⇒ x = ∆ x ∆ = — 78 — 78 = 1 ∆ y = 4 10 0 1 1 — 3 3 — 5 1 = — 156 ⇒ y = ∆ y ∆ = — 156 — 78 = 2 ∆ z = 4 3 10 1 0 1 3 — 4 — 5 = 0 ⇒ z = ∆ z ∆ = 0 — 78 = 0
Таким образом, проекцией заданной точки на прямую a является точка c координатами ( 1 , 2 , 0 )
- На основе заданных канонических уравнений легко записать параметрические уравнения прямой в пространстве:
x + 2 3 = y — 6 — 4 = z + 1 1 ⇔ x = — 2 + 3 · λ y = 6 — 4 · λ z = — 1 + λ
Подставим в уравнение плоскости, имеющее вид 3 x — 4 y + z + 5 = 0 , вместо x , y и z их выражения через параметр:
3 · ( — 2 + 3 · λ ) — 4 · ( 6 — 4 · λ ) + ( — 1 + λ ) + 5 = 0 ⇔ 26 · λ = 0 ⇔ λ = 1
Вычислим искомые координаты точки пересечения прямой a и плоскости α по параметрическим уравнениям прямой a при λ = 1 :
x = — 2 + 3 · 1 y = 6 — 4 · 1 z = — 1 + 1 ⇔ x = 1 y = 2 z = 0
Таким образом, проекция заданной точки на прямую a имеет координаты ( 1 , 2 , 0 )
Ответ: ( 1 , 2 , 0 )
Напоследок отметим, что проекциями точки М 1 ( x 1 , y 1 , z 1 ) на координатные прямые O x , O y и O z буду являться точки с координатами ( x 1 , 0 , 0 ) , ( 0 , y 1 , 0 ) и ( 0 , 0 , z 1 ) соответственно.
Видео:23. Точка пересечения прямой и плоскости / Проекция точки на плоскость / Проекция точки на прямуюСкачать

Проекция точки на прямую онлайн
С помощю этого онлайн калькулятора можно найти проекцию точки на прямую. Дается подробное решение с пояснениями. Для вычисления проекции точки на прямую, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:2 3 проекция точки на конусеСкачать

Проекция точки на прямую − теория, примеры и решения
Рассмотрим эту задачу в двухмерном и трехмерном пространствах.
1. Пусть в двухмерном пространстве задана точка M0(x0, y0) и прямая L:
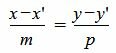 , , | (1) |
где q=(m,p) направляющий вектор прямой L.
Найдем проекцию точки M0 на прямую (1)(Рис.1).
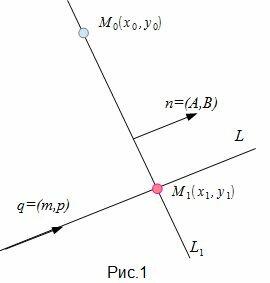 |
Алгоритм нахождения проекции точки на прямую L содержит следующие шаги:
- построить прямую L1, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение прямых L и L1(точка M1)
Уравнение прямой, проходящей через точку M0(x0, y0) имеет следующий вид:
| A(x−x0)+B(y−y0)=0 | (2) |
Как видно из рисунка Рис.1, для того, чтобы прямая L1 была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L1, поэтому в качестве нормального вектора прямой L1 достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L1, представленной уравнением (2) можно записать так:
| m(x−x0)+p(y−y0)=0 | (3) |
| mx+py−mx0−py0=0 | (4) |
Для нахождения точки пересечения прямых L и L1, которая и будет проекцией точки M0 на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M1(x1, y1).
Найдем точку пересечения прямых L и L1 другим методом.
Выведем параметрическое уравнение прямой (1):
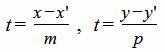 |
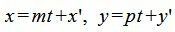 | (5) |
Подставим значения x и y в (4):
| m(mt+x’)+p(pt+y’)−mx0−py0=0 |
| m 2 t+mx’+p 2 t+py’−mx0−py0=0 |
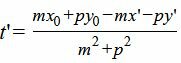 | (5′) |
Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L1(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M0 на прямую L:
Пример 1. Найти проекцию точки M0(1, 3) на прямую
 | (6) |
Направляющий вектор прямой (6) имеет вид:
Т.е. m=4, p=5. Из уравнения прямой (6) видно, что она проходит через точку M’ (x’, y’)=(2, −3)(в этом легко убедится − подставляя эти значения в (6) получим тождество 0=0), т.е. x’=2, y’=-3. Подставим значения m, p, x0, y0, x’, y’ в (5′):
 |
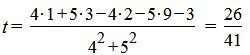 |
Подставляя значение t в (5), получим:
 , , |
 . . |
Проекцией точки M0(1, 3) на прямую (6) является точка:
 |
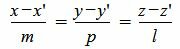 , , | (7) |
где q=(m, p, l) направляющий вектор прямой L.
Найдем проекцию точки M0 на прямую (7)(Рис.2).
 |
Нахождение проекцию точки на прямую L содержит следующие шаги:
- построить плоскость α, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение плоскости α и прямой L(точка M1)
| A(x−x0)+B(y−y0)+C(z−z0)=0 | (8) |
где n=(A,B,C) нормальный вектор плоскости α.
Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (8) можно записать так:
| m(x−x0)+p(y−y0)+l(z−z0)=0 |
| mx+py+lz−mx0−py0−lz0=0 | (9) |
Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M0 на прямую L, выведем параметрическое уравнение прямой (7):
 |
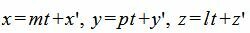 | (10) |
Подставим значения x и y в (9):
| m(mt+x’)+p(pt+y’)+l(lt+z’)−mx0−py0−lz0=0 |
| m 2 t+mx’+p 2 t+py’+l 2 t+ly’−mx0−py0−lz0=0 |
 | (10′) |
Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (9). Следовательно, подставляя значение t’ в (10) получим координаты проекции точки M0 на прямую L:
| M1(x1, y1, , z1), |
Пример 2. Найти проекцию точки M0(3, −1, −2) на прямую
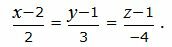 | (11) |
Направляющий вектор прямой (11) имеет вид:
Т.е. m=2, p=3, l=−4. Из уравнения прямой (11) видно, что она проходит через точку M’ (x’, y’, z’)=(2, 1, 1)(в этом легко убедится − подставляя эти значения в (11) получим тождество 0=0=0), т.е. x’=2, y’=1, z’=1. Подставим значения m, p, l x0, y0, z0 x’, y’, z’ в (10′):
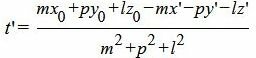 |
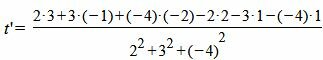 |
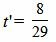 |
Подставляя значение t=t’ в (10), получим:
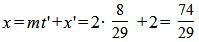 . . |
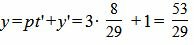 . . |
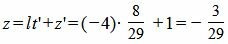 . . |
Проекцией точки M0(3, −1, −2) на прямую (11) является точка:
Видео:Проекция точки на плоскость, проекция прямой на плоскость. Параллельные прямые.Скачать

Как найти проекцию точки на плоскость: методика определения и пример решения задачи
При решении геометрических задач в пространстве часто возникает проблема определения расстояния между плоскостью и точкой. В некоторых случаях это необходимо для комплексного решения. Эту величину можно вычислить, если найти проекцию на плоскость точки. Рассмотрим этот вопрос подробнее в статье.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнение для описания плоскости
Перед тем как перейти к рассмотрению вопроса касательно того, как найти проекцию точки на плоскость, следует познакомиться с видами уравнений, которые задают последнюю в трехмерном пространстве. Подробнее — ниже.
Уравнением общего вида, определяющим все точки, которые принадлежат данной плоскости, является следующее:
Первые три коэффициента — это координаты вектора, который называется направляющим для плоскости. Он совпадает с нормалью для нее, то есть является перпендикулярным. Этот вектор обозначают n¯(A; B; C). Свободный коэффициент D однозначно определяется из знания координат любой точки, принадлежащей плоскости.
Далее в статье будем использовать записанное уравнение. Оно требуется, чтобы найти проекцию точки на плоскость.
Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Понятие о проекции точки и ее вычисление
Предположим, что задана некоторая точка P(x1; y1; z1) и плоскость. Она определена уравнением в общем виде. Если провести перпендикулярную прямую из P к заданной плоскости, то очевидно, что она пересечет последнюю в одной определенной точке Q (x2; y2; z2). Q называется проекцией P на рассматриваемую плоскость. Длина отрезка PQ называется расстоянием от точки P до плоскости. Таким образом, сам PQ является перпендикулярным плоскости.
Как можно найти координаты проекции точки на плоскость? Сделать это не сложно. Для начала следует составить уравнение прямой, которая будет перпендикулярна плоскости. Ей будет принадлежать точка P. Поскольку вектор нормали n¯(A; B; C) этой прямой должен быть параллелен, то уравнение для нее в соответствующей форме запишется так:
Где λ — действительное число, которое принято называть параметром уравнения. Изменяя его, можно получить любую точку прямой.
После того как записано векторное уравнение для перпендикулярной плоскости линии, необходимо найти общую точку пересечения для рассматриваемых геометрических объектов. Ее координаты и будут проекцией P. Поскольку они должны удовлетворять обоим равенствам (для прямой и для плоскости), то задача сводится к решению соответствующей системы линейных уравнений.
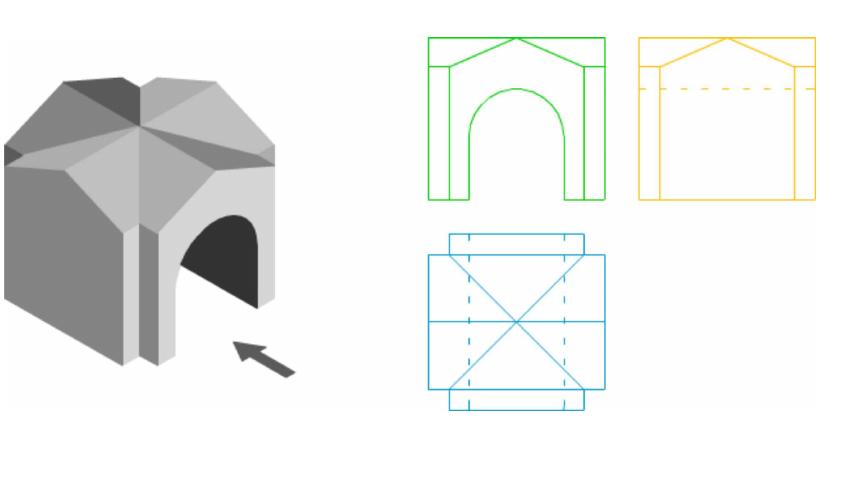
Понятие проекции часто используется при изучении чертежей. На них изображаются боковые и горизонтальные проекции детали на плоскости zy, zx, и xy.
Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Вычисление расстояния от плоскости до точки
Как выше было отмечено, знание координат проекции на плоскость точки позволяет определить дистанцию между ними. Используя обозначения, введенные в предыдущем пункте, получаем, что искомое расстояние равно длине отрезка PQ. Для его вычисления достаточно найти координаты вектора PQ¯, а затем рассчитать его модуль по известной формуле. Конечное выражение для d расстояния между P точкой и плоскостью принимает вид:
Полученное значение d представлено в единицах, в которых задается текущая декартова координатная система xyz.
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Пример задачи
Допустим, имеется точка N(0; -2; 3) и плоскость, которая описывается следующим уравнением:
Следует найти точки проекцию на плоскость и вычислить между ними расстояние.
В первую очередь составим уравнение прямой, которая пересекает плоскость под углом 90 o . Имеем:
Записывая это равенство в явном виде, приходим к следующей системе уравнений:
Подставляя значения координат из первых трех равенств в четвертое, получим значение λ, определяющее координаты общей точки прямой и плоскости:
Подставим найденный параметр в уравнение прямой и найдем координаты проекции исходной точки на плоскость:
Для вычисления дистанции между заданными в условии задачи геометрическими объектами применим формулу для d:
d = √((3 — 0 ) 2 + (-3,5 + 2 ) 2 + (4,5 — 3 ) 2 ) = 3,674.
В данной задаче мы показали, как находить проекцию точки на произвольную плоскость и как вычислять между ними расстояние.
🎦 Видео
Проецирование точкиСкачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

523. Проекция точки на плоскость.Скачать

проекции точкиСкачать

12. Уравнения прямой в пространстве Решение задачСкачать

Построение проекций точек на поверхности предметовСкачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Нахождение точки, симметричной данной относительно плоскости в пространствеСкачать

Параметрические уравнения прямойСкачать

Найти точку пересечения прямой и плоскостиСкачать