Решение уравнений в математике занимает особое место. Этому процессу предшествует множество часов изучения теории, в ходе которых ученик узнает способы решения уравнений, определения их вида и доводит навык до полного автоматизма. Однако далеко не всегда поиск корней имеет смысл, так как их может попросту не быть. Существуют особые приемы нахождения корней. В данной статье мы разберем основные функции, их области определения, а также случаи, когда их корни отсутствуют.
- Какое уравнение не имеет корней?
- 1. Линейное уравнение
- 2. Квадратное уравнение
- 3. Тригонометрические уравнения
- 4. Системы уравнений
- Обобщение и советы по нахождению корней уравнения
- Неполные квадратные уравнения
- теория по математике 📈 уравнения
- Неполное квадратное уравнение при b=0: ax 2 +c=0
- Неполное квадратное уравнение при с=0: ax 2 +bx=0
- Неполное квадратное уравнение с коэффициентами b и с равными нулю: ax 2 =0
- Показательные уравнения и неравенства с примерами решения
- Решении показательных уравнений
- Показательные уравнения и их системы
- Пример №1
- Пример №2
- Пример №3
- Пример №4
- Пример №5
- Пример №6
- Системы простейших показательных уравнений
- Пример №7
- Пример №8
- Пример №9
- Приближенное решение уравнений
- Пример №10
- Нахождение приближенного корня с заданной точностью
- Пример №11
- 📹 Видео
Видео:Как найти значения переменной, при которых алгебраическая дробь не имеет смысла?Скачать

Какое уравнение не имеет корней?
Уравнение не имеет корней в том случае, если не существует таких действительных аргументов х, при которых уравнение тождественно верно. Для неспециалиста данная формулировка, как и большинство математических теорем и формул, выглядит очень размытой и абстрактной, однако это в теории. На практике все становится предельно просто. Например: уравнение 0 * х = -53 не имеет решения, так как не найдется такого числа х, произведение которого с нулем дало бы что-то, кроме нуля.
Сейчас мы рассмотрим самые базовые типы уравнений.
Видео:Установите при каких значениях переменной не имеет смысла алгебраическая дробьСкачать

1. Линейное уравнение
Уравнение называется линейным, если его правая и левая части представлены в виде линейных функций: ax + b = cx + d или в обобщенном виде kx + b = 0. Где а, b, с, d — известные числа, а х — неизвестная величина. Какое уравнение не имеет корней? Примеры линейных уравнений представлены на иллюстрации ниже.
В основном линейные уравнения решаются простым переносом числовой части в одну часть, а содержимого с х — в другую. Получается уравнение вида mx = n, где m и n — числа, а х — неизвестное. Чтобы найти х, достаточно разделить обе части на m. Тогда х = n/m. В основном линейные уравнения имеют только один корень, однако бывают случаи, когда корней либо бесконечно много, либо нет вовсе. При m = 0 и n = 0 уравнение принимает вид 0 * х = 0. Решением такого уравнения будет абсолютно любое число.
Однако какое уравнение не имеет корней?
При m = 0 и n = 0 уравнение не имеет корней из множества действительных чисел. 0 * х = -1; 0 * х = 200 — эти уравнения не имеют корней.
Видео:6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

2. Квадратное уравнение
Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0 при а = 0. Самым распространенным способом решения квадратного уравнения является решение через дискриминант. Формула нахождения дискриминанта квадратного уравнения: D = b 2 — 4 * a * c. Далее находится два корня х1,2= (-b ± √D) / 2 * a.
При D > 0 уравнение имеет два корня, при D = 0 — корень один. Но какое квадратное уравнение не имеет корней? Пронаблюдать количество корней квадратного уравнения проще всего по графику функции, представляющем собой параболу. При а > 0 ветви направлены вверх, при а 2 – 8x + 72 = 0 не имеет корней, так как имеет отрицательный дискриминант D = (–8) 2 – 4 * 1 * 72 = -224. Это значит, что парабола не касается оси абсцисс и функция никогда не принимает значение 0, следовательно, уравнение не имеет действительных корней.
Видео:Вариант 36, № 3. Значение переменной, при котором выражение (дробь) не имеет смысла. Пример 1Скачать

3. Тригонометрические уравнения
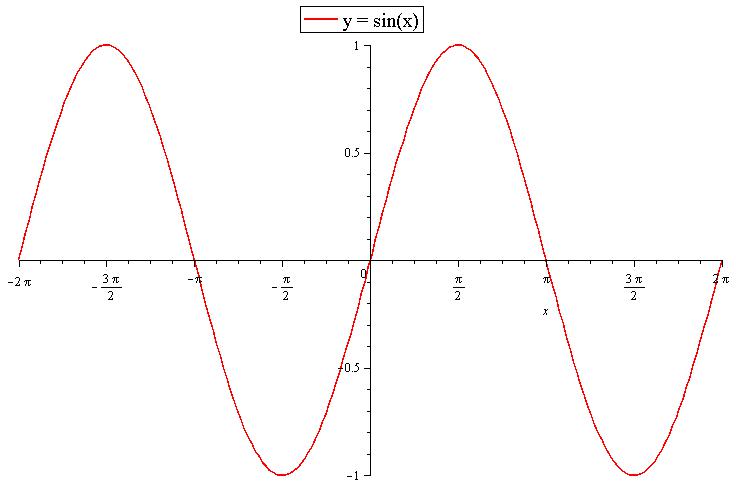
Тригонометрические функции рассматриваются на тригонометрической окружности, однако могут быть представлены и в декартовой системе координат. В данной статье мы рассмотрим две основные тригонометрические функции и их уравнения: sinx и cosx. Так как данные функции образуют тригонометрическую окружность с радиусом 1, |sinx| и |cosx| не могут быть больше 1. Итак, какое уравнение sinx не имеет корней? Рассмотрим график функции sinx, представленный на картинке ниже.
Мы видим, что функция является симметричной и имеет период повторения 2pi. Исходя их этого, можно говорить, что максимальным значением этой функции может быть 1, а минимальным -1. Например, выражение cosx = 5 не будет иметь корней, так как по модулю оно больше единицы.
Это самый простой пример тригонометрических уравнений. На самом деле их решение может занимать множество страниц, в конце которых вы осознаете, что использовали неправильную формулу и все нужно начинать сначала. Порой даже при правильном нахождении корней вы можете забыть учесть ограничения по ОДЗ, из-за чего в ответе появляется лишний корень или интервал, и весь ответ обращается в ошибочный. Поэтому строго следите за всеми ограничениями, ведь не все корни вписываются в рамки задачи.
Видео:Как определить, при каких значениях переменной алгебраическая дробь имеет смысл?Скачать
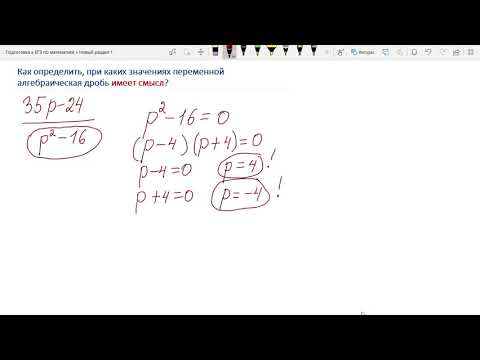
4. Системы уравнений
Система уравнений представляет собой совокупность уравнений, объединенных фигурной или квадратной скобками. Фигурные скобки обозначают совместное выполнение всех уравнений. То есть если хотя бы одно из уравнений не имеет корней или противоречит другому, вся система не имеет решения. Квадратные скобки обозначают слово «или». Это значит, что если хотя бы одно из уравнений системы имеет решение, то вся система имеет решение.
Ответом системы с квадратными скобками является совокупность всех корней отдельных уравнений. А системы с фигурным скобками имеют только общие корни. Системы уравнений могут включать абсолютно разнообразные функции, поэтому такая сложность не позволяет сказать сразу, какое уравнение не имеет корней.
Видео:Задача №39. Алгебра 7 класс Макарычев.Скачать

Обобщение и советы по нахождению корней уравнения
В задачниках и учебниках встречаются разные типы уравнений: такие, которые имею корни, и не имеющие их. В первую очередь, если у вас не получается найти корни, не думайте, что их нет совсем. Возможно, вы совершили где-нибудь ошибку, тогда достаточно лишь внимательно перепроверить ваше решение.
Мы рассмотрели самые базовые уравнения и их виды. Теперь вы можете сказать, какое уравнение не имеет корней. В большинстве случаев сделать это совсем не трудно. Для достижения успеха в решении уравнений требуется лишь внимание и сосредоточенность. Практикуйтесь больше, это поможет вам ориентироваться в материале гораздо лучше и быстрее.
Итак, уравнение не имеет корней, если:
- в линейном уравнении mx = n значение m = 0 и n = 0;
- в квадратном уравнении, если дискриминант меньше нуля;
- в тригонометрическом уравнении вида cosx = m / sinx = n, если |m| > 0, |n| > 0;
- в системе уравнений с фигурными скобками, если хотя бы одно уравнение не имеет корней, и с квадратными скобками, если все уравнения не имеют корней.
Видео:Когда алгебраическая дробь равна 0?Скачать

Неполные квадратные уравнения
теория по математике 📈 уравнения
Квадратным уравнением называется уравнение вида ax 2 +bx+c=0, где х – переменная, a, b, c некоторые числа, причем a≠0. Обычно его называют полным квадратным уравнением.
Если в таком уравнении один из коэффициентов b или c равен нулю, либо оба одновременно равны нулю, то такое уравнение называется неполным квадратным уравнением.
Неполное квадратное уравнение при b=0: ax 2 +c=0
Для решения такого вида уравнения надо выполнить перенос коэффициента с в правую часть, затем найти квадрат переменной (делим обе части на одно и то же число), найти два
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Пример №1. Решить уравнение:
Выполним перенос числа –45 в правую часть, изменяя знак на противоположный: 5х 2 =45; найдем переменную в квадрате, поделив обе части уравнения на 5: х 2 =9. Видим, что квадрат переменной равен положительному числу, поэтому уравнение имеет два корня, находим их устно, извлекая квадратный
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Ответ: х=±3 или можно записать ответ так: х1=–3, х2=3 (обычно меньший корень записывают первым). Пример №2. Решить уравнение:
Выполним решение уже известным способом: –6х 2 =90. х 2 =–15 Здесь видим, что квадрат переменной равен отрицательному числу, а это значит, что уравнение не имеет корней. Ответ: нет корней. Пример №3. Решить уравнение:
Здесь мы видим в левой части уравнения формулу сокращенного умножения (разность квадратов двух выражений). Поэтому, можем разложить данное выражение на множители, и найти корни уравнения: (х–10)(х+10)=0. Соответственно, вспомним, что произведение двух множителей равно нулю тогда, когда хотя бы один из множителей равен нулю, то есть х–10=0 или х+10=0. Откуда имеем два корня х1=10, х2=–10.
Неполное квадратное уравнение при с=0: ax 2 +bx=0
Данного вида уравнение решается способом разложения на множители – вынесением за скобки переменной. Данное уравнение всегда имеет два корня, один из которых равен нулю. Рассмотрим данный способ на примерах.
Пример №4. Решить уравнение:
Выносим переменную х за скобки: х(х+8)=0. Получаем два уравнения х=0 или х+8=0. Отсюда данное уравнение имеет два корня – это 0 и –8.
Пример №5. Решить уравнение:
Здесь кроме переменной можно вынести за скобки еще и коэффициент 3, который является общим множителем для данных в уравнении коэффициентов. Получим: 3х(х–4)=0. Получаем два уравнения 3х=0 и х–4=0. Соответственно и два корня – нуль и 4.
Неполное квадратное уравнение с коэффициентами b и с равными нулю: ax 2 =0
Данное уравнение при любых значениях коэффициента а будет иметь один корень, равный нулю.
Пример №6. Решить уравнение:
Обе части уравнения делим на (–14) и получаем х 2 =0, откуда соответственно и единственный корень – нуль. Пример №6. Решить уравнение:
Также делим обе части на 23 и получаем х 2 =0. Значит, корень уравнения – нуль.
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Показательные уравнения и неравенства с примерами решения
Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными.
Видео:АЛГЕБРА 7 класс : Выражения с переменнымиСкачать

Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Пусть
Каждому значению показательной функции 
Пример:
Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
Пример:
Решение:
а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ:
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решение:
а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. 
б) Разделив обе части уравнения на 

Ответ:
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение
Решение:
Обозначим 
Таким образом, из данного уравнения получаем
откуда находим:
Итак, с учетом обозначения имеем:
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Пример:
Решить уравнение
Решение:
Пример:
При каком значении а корнем уравнения 
Решение:
Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду 
Пример №1
Решите уравнение
Решение:
Заметим, что 
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.
Пример №2
Решить уравнение
Решение:
Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем
Последнее уравнение равносильно уравнению 4х-19 = 2,5х.
2 Введение новой переменной.
Пример №3
Решить уравнение
Решение:
Применив тождество 2, перепишем уравнение как
Введем новую переменную: 
которое имеет корни 


Пример №4
Решить уравнение
Решение:
Разделив обе части уравнения на 
последнее уравнение запишется так:
Решая уравнение, найдем
Значение 

Пример №5
Решить уравнение
Решение:
Заметим что 
Перепишем уравнение в виде
Обозначим 
Получим
Корнями данного уравнения будут
Следовательно,
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение
Решение:
После вынесения за скобку в левой части 



Системы простейших показательных уравнений
Пример №7
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей
системе :
Очевидно, что последняя система имеет решение
Пример №8
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем 
Пример №9
Решите систему уравнений:
Решение:
Сделаем замену: 
Очевидно, что эта система уравнений имеет решение
Тогда получим уравнения
Приближенное решение уравнений
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть 

Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок 
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
- вычисляется значение f(х) выражения
- отрезок делится пополам, то есть вычисляется значение
- вычисляется значение
выражения f(х) в точке
- проверяется условие
- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
(левый конец отрезка переходит в середину);
- если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие
- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения 
Оказывается, что для корня 


Пример №10
Найдите интервал, содержащий корень уравнения
Решение:
Поделив обе части уравнения на 2 , получим,
Так как, для нового уравнения
Значит, в интервале, 




Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство 



корень уравнения с точностью 




Пример №11
Найдите приближенное значение корня уравнения 
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что 
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если
Пусть
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📹 Видео
Допустимые значения переменной в рациональном выраженииСкачать

Выражение не имеет смысла. Алгебра 8 класс.Скачать

8 класс. Алгебра. При каких значениях переменной имеет смысл выражениеСкачать

Система уравнений не имеет решений или имеет бесчисленное множество решенийСкачать

#118 Урок 43 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Скачать

311 Алгебра 9 класс. При каких значениях t Уравнение не имеет корнейСкачать

Урок 2 ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ 7 КЛАСССкачать

9кл. При каких значения переменной имеет смысл выражениеСкачать

При каких значениях переменной имеет смысл выражениеСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать


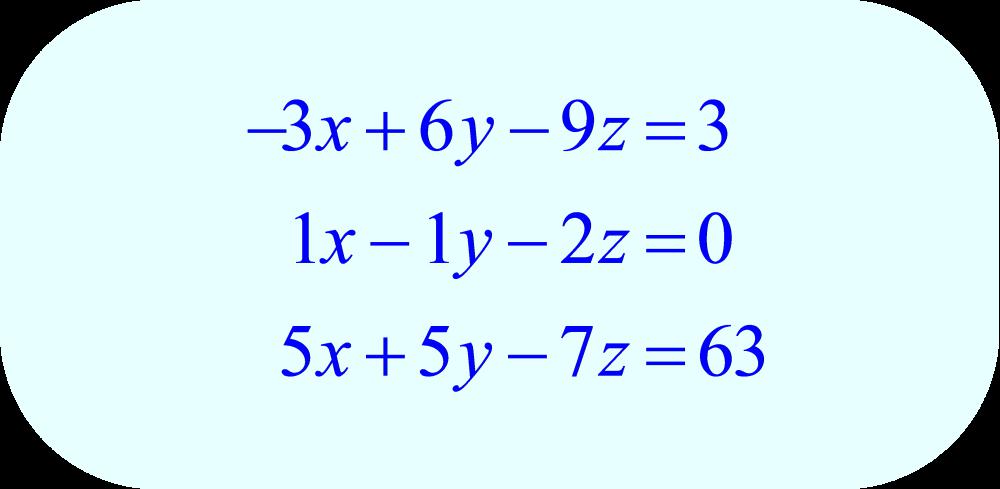










































































 выражения f(х) в точке
выражения f(х) в точке 

 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину);










