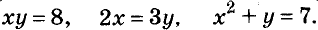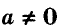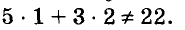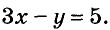- Уравнения в целых числах
- Немного теории
- Задачи с решениями
- Задачи без решений
- Объясните, пожалуйста, как решать такое задание :Найдите все пары целых чисел (x ; y), удовлетворяющих уравнению 7x + 4y = 123?
- Найдите все пары целых чисел, удовлетворяющих уравнениюа)ху = 17?
- Найдите все пары натуральных чисел удовлетворяющих уравнению xy — 2x — y = 9?
- Найдите все пары натуральных чисел, удовлетворяющих уравнению ху — 2х — у = 11?
- Найдите такую пару чисел, удовлетворяющую уравнению 3x + 5y = 19, сумма которых равна 5 ?
- Объясните пожалуйста, как решать такие уравнения?
- Найдите все пары целых чисел (х ; у), удовлетворяющие уравнению 4у — х = 27?
- Найдите все пары целых чисел, удовлетворяющие уравнению 4x ^ 2 — y ^ 2 = 3?
- Найдите все пары целых чисел , удовлетворяющие уравнению х ^ 2 — 4y ^ 2 = 5?
- Как РЕШАТЬ задания такого типа, объясните пожалуйста?
- Найдите пары целых чисел (x ; y) удовлетворяющих уравнению 2y + x = 15?
- Системы линейных уравнений с примерами решений
- Уравнения с двумя переменными
- 💡 Видео
Видео:202 Алгебра 8 класс Найдите все пары целых чисел удовлетворяющие уравниниюСкачать

Уравнения в целых числах
Немного теории
Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.
Современной постановкой диофантовых задач мы обязаны французскому математику Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение
не имеет ненулевых рациональных решений для всех натуральных n > 2.
Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.
В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.
При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:
способ перебора вариантов;
применение алгоритма Евклида;
представление чисел в виде непрерывных (цепных) дробей;
разложения на множители;
решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;
метод бесконечного спуска.
Задачи с решениями
1. Решить в целых числах уравнение x 2 – xy – 2y 2 = 7.
Запишем уравнение в виде (x – 2y)(x + y) = 7.
Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:
1) x – 2y = 7, x + y = 1;
2) x – 2y = 1, x + y = 7;
3) x – 2y = –7, x + y = –1;
4) x – 2y = –1, x + y = –7.
Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).
Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).
2. Решить в целых числах уравнение:
а) 20х + 12у = 2013;
в) 201х – 1999у = 12.
а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.
Ответ: решений нет.
б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,
Поскольку числа 5 и 7 взаимно простые, то
Значит, общее решение:
х = 1 + 7k, у = 2 – 5k,
где k – произвольное целое число.
Ответ: (1+7k; 2–5k), где k – целое число.
в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:
НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.
Запишем этот процесс в обратном порядке:
1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =
= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =
= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.
Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел
x0 = 1273·12 = 15276, y0 = 128·12 = 1536
является решением уравнения 201х – 1999у = 12.
Общее решение этого уравнения запишется в виде
х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,
или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),
х = 1283 + 1999n, у = 129 + 201n, где n – целое число.
Ответ: (1283+1999n, 129+201n), где n – целое число.
3. Решить в целых числах уравнение:
а) x 3 + y 3 = 3333333;
б) x 3 + y 3 = 4(x 2 y + xy 2 + 1).
а) Так как x 3 и y 3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x 3 + y 3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
б) Перепишем исходное уравнение в виде (x + y) 3 = 7(x 2 y + xy 2 ) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
а) в простых числах уравнение х 2 – 7х – 144 = у 2 – 25у;
б) в целых числах уравнение x + y = x 2 – xy + y 2 .
а) Решим данное уравнение как квадратное относительно переменной у. Получим
у = х + 9 или у = 16 – х.
Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).
Так как х, у – простые, то из равенства у = 16 – х имеем
С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).
Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).
б) Рассмотрим данное уравнение как квадратное уравнение относительно x:
x 2 – (y + 1)x + y 2 – y = 0.
Дискриминант этого уравнения равен –3y 2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.
Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).
5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x 2 + y 2 + z 2 = x 3 + y 3 + z 3 ?
Попробуем подбирать такие тройки, где у = –z. Тогда y 3 и z 3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь вид
Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно много, а именно, это все числа вида 2n 2 +1. Подставляя в x 2 (x–1) = 2y 2 такое число, после несложных преобразований получаем:
y = xn = n(2n 2 +1) = 2n 3 +n.
Все тройки, полученные таким образом, имеют вид (2n 2 +1; 2n 3 +n; –2n 3 – n).
6. Найдите такие целые числа x, y, z, u, что x 2 + y 2 + z 2 + u 2 = 2xyzu.
Число x 2 + y 2 + z 2 + u 2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел.
Если все четыре числа x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 делится на 4, но при этом 2xyzu не делится на 4 – несоответствие.
Если ровно два из чисел x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 не делится на 4, а 2xyzu делится на 4 – опять несоответствие.
Поэтому все числа x, y, z, u чётны. Тогда можно записать, что
и исходное уравнение примет вид
Теперь заметим, что (2k + 1) 2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x1, y1, z1, u1 нечётны, то x1 2 + y1 2 + z1 2 + u1 2 не делится на 8. А если ровно два из этих чисел нечётно, то x1 2 + y1 2 + z1 2 + u1 2 не делится даже на 4. Значит,
и мы получаем уравнение
Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2 n при всех натуральных n, что возможно лишь при x = y = z = u = 0.
7. Докажите, что уравнение
(х – у) 3 + (y – z) 3 + (z – x) 3 = 30
не имеет решений в целых числах.
Воспользуемся следующим тождеством:
(х – у) 3 + (y – z) 3 + (z – x) 3 = 3(х – у)(y – z)(z – x).
Тогда исходное уравнение можно записать в виде
(х – у)(y – z)(z – x) = 10.
Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде
Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5, либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в целых числах.
8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у 2 .
если х = 1, то у 2 = 1,
если х = 3, то у 2 = 9.
Этим случаям соответствуют следующие пары чисел:
Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как
5! + 6! + . . . + х! = 10n,
можем записать, что
1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.
Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.
Ответ: (1; 1), (1; –1), (3; 3), (3; –3).
9. Решите следующую систему уравнений в натуральных числах:
a 3 – b 3 – c 3 = 3abc, a 2 = 2(b + c).
3abc > 0, то a 3 > b 3 + c 3 ;
таким образом имеем
b 2 2 + х = у 4 + у 3 + у 2 + у.
Разложив на множители обе части данного уравнения, получим:
х(х + 1) = у(у + 1)(у 2 + 1),
х(х + 1) = (у 2 + у)(у 2 + 1)
Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому, приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных:
Произведение (у 2 + у)(у 2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля, только при у = 2. Поэтому х(х + 1) = 30, откуда х5 = 5, х6 = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих исходному уравнению:
Ответ: (0; 0), (0; –1), (–1; 0), (–1; –1), (5; 2), (–6; 2.)
Задачи без решений
1. Решить в целых числах уравнение:
б) х 2 + у 2 = х + у + 2.
2. Решить в целых числах уравнение:
а) х 3 + 21у 2 + 5 = 0;
б) 15х 2 – 7у 2 = 9.
3. Решить в натуральных числах уравнение:
4. Доказать, что уравнение х 3 + 3у 3 + 9z 3 = 9xyz в рациональных числах имеет единственное решение
5. Доказать, что уравнение х 2 + 5 = у 3 в целых числах не имеет решений.
Видео:Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Объясните, пожалуйста, как решать такое задание :Найдите все пары целых чисел (x ; y), удовлетворяющих уравнению 7x + 4y = 123?
Алгебра | 5 — 9 классы
Объясните, пожалуйста, как решать такое задание :
Найдите все пары целых чисел (x ; y), удовлетворяющих уравнению 7x + 4y = 123.
Линейное диофантово уравнение 7х + 4у = 123.
Если коэффициенты перед х и упростые числа, то это уравнение имеет решение в целых числах.
НОД(7, 4) = 1 ⇒ 7 и 4 — простые числа.
Подберём частное решение $(x_0,y_0)$ .
В этом уравнении это сделать не совсем просто, поэтому воспользуемся теоремой :
чтобы найти решение уравнения ах + ву = с при взаимно — простых а и в, нужно найти решение$(x_0,y_0)$ уравнения ах + ву = 1.
Тогдачисла $(cx_0,cy_0)$ составляют решение
уравнения ах + ву = с .
7х + 4у = 1 ⇒ $x_0=-1; ,; ; y_0=2$ .
$7cdot (-1)+4cdot 2=-7+8=1$
$cx_0=123cdot (-1)=-123; ,; ; cy_0=2cdot 123=246; ; to \\7x+4y=123; ; (star)\\7cdot (-123)+4cdot 246=123; ; (star star )$
Из ( * ) вычтем ( * * ) , получим :
Чтобы (у — 246) было целым, надо чтобы (х + 123) нацело делилось на 4, то есть х + 123 = 4к ⇒ х = 4к — 123 , k∈Z .
Тогда $y-246= frac =-7k; ; Rightarrow ; ; y=-7k+246$
Видео:202 Алгебра 8 класс, Найдите все пары целых чисел удовлетворяющие уравнениюСкачать

Найдите все пары целых чисел, удовлетворяющих уравнениюа)ху = 17?
Найдите все пары целых чисел, удовлетворяющих уравнению
Видео:ЕГЭ математика С6.Пары натуральных чисел. Видео урок.Скачать

Найдите все пары натуральных чисел удовлетворяющих уравнению xy — 2x — y = 9?
Найдите все пары натуральных чисел удовлетворяющих уравнению xy — 2x — y = 9.
Видео:Найти все пары чисел #математика #уравнения #алгебра #репетиторСкачать

Найдите все пары натуральных чисел, удовлетворяющих уравнению ху — 2х — у = 11?
Найдите все пары натуральных чисел, удовлетворяющих уравнению ху — 2х — у = 11.
Видео:Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

Найдите такую пару чисел, удовлетворяющую уравнению 3x + 5y = 19, сумма которых равна 5 ?
Найдите такую пару чисел, удовлетворяющую уравнению 3x + 5y = 19, сумма которых равна 5 .
Видео:Найдите все пары натуральных чисел x y удовлетворяющих равенству xy 38x + 38yСкачать

Объясните пожалуйста, как решать такие уравнения?
Объясните пожалуйста, как решать такие уравнения?
Видео:Изображение множества точек на координатной плоскости, удовлетворяющих уравнению.Скачать

Найдите все пары целых чисел (х ; у), удовлетворяющие уравнению 4у — х = 27?
Найдите все пары целых чисел (х ; у), удовлетворяющие уравнению 4у — х = 27.
Видео:Решите систему уравнений в целых числахСкачать

Найдите все пары целых чисел, удовлетворяющие уравнению 4x ^ 2 — y ^ 2 = 3?
Найдите все пары целых чисел, удовлетворяющие уравнению 4x ^ 2 — y ^ 2 = 3.
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Найдите все пары целых чисел , удовлетворяющие уравнению х ^ 2 — 4y ^ 2 = 5?
Найдите все пары целых чисел , удовлетворяющие уравнению х ^ 2 — 4y ^ 2 = 5.
Видео:Найти все пары целых чисел для которых верны неравенстваСкачать

Как РЕШАТЬ задания такого типа, объясните пожалуйста?
Как РЕШАТЬ задания такого типа, объясните пожалуйста.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Найдите пары целых чисел (x ; y) удовлетворяющих уравнению 2y + x = 15?
Найдите пары целых чисел (x ; y) удовлетворяющих уравнению 2y + x = 15.
На этой странице сайта, в категории Алгебра размещен ответ на вопрос Объясните, пожалуйста, как решать такое задание :Найдите все пары целых чисел (x ; y), удовлетворяющих уравнению 7x + 4y = 123?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.
√((x — 2) / (1 — 2x))> — 1 ОДЗ : (x — 2) / (2x — 1)≥0 — ∞__ — __1 / 2__ + __2__ — __ + ∞ x∈[1 / 2 ; 2] 1 — 2x≠0 2x≠1 x≠1 / 2 ⇒ x∈(1 / 2 ; 2]. (√((x — 2) / (1 — 2x)))²>( — 1)² (x — 2) / (1 — 2x)>1 x — 2>1 — 2x 3x>3 |÷3 x>1⇒ Ответ : x∈(1 ; 2].
2 2 25b — 30ab + 9a Это ответ, думаю что правильно.
25b(2 кводрат) — 9а(кводрат).
Вот решения на все твои вопросы).
√113 ^ 2 — 112 ^ 2 = 113 — 112 ^ 2 = — 12431 √3 ^ 6 * 5 ^ 2 = 3 ^ 3 * 25 = 27 * 25 = 675 √6 ^ 4 * 2 ^ 6 = 6 ^ 2 * 2 ^ 6 = 36 * 64 = 2304.
2p — 3p + ( — 2b + c) = 2p — 3p — 2b + c = — p — 2b + c.
Пусть угол между боковыми сторонамиравен х, тогда угол при основанииравен 7х. В равнобедренном треугольнике углы при основании равны. И т. к. Сумма углов в треугольнике равна180°, то получим уравнение : 7х + 7х + х = 180 15х = 180 х = 12° — угол м..
В равнобедренном треугольнике углы при основании равны. Обозначим угол при вершине через x, тогда углы при основании каждый 7x. Cумма углов в треугольнике равна 180°, составим и решим уравнение. X + 7x + 7x = 180 15x = 180 x = 12° — угол при верши..
Видео:Упорядоченные парыСкачать

Системы линейных уравнений с примерами решений
Содержание:
Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:
- уравнения с двумя переменными;
- график линейного уравнения;
- системы уравнений;
- способ подстановки;
- способ сложения;
- решение задач составлением системы уравнений.
Уравнения с двумя переменными
До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.
Пример:
На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?
Решение:
Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.
Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:
Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если
Примеры линейных уравнений:
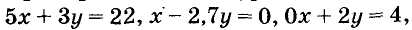
Паре чисел х = -1 и у = 9 удовлетворяет уравнение 5х + Зу -= 22, так как 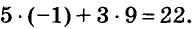
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.
Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.
Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.
Для примера найдем несколько решений уравнения
Если х = 1, то 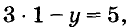
Уравнение 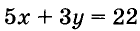
Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.
Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.
Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.
Например, уравнение 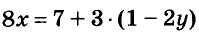
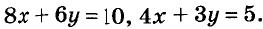
Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению 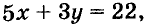
Переменную у из этого уравнения выразим через х:
Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.
Пример:
Решение:
а) При любых значениях х и у значения выражения 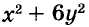
б) Значение выражения 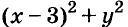
Пример:
Составьте уравнение с двумя переменными, решением которого будет пара чисел (1; -5).
Решение:
Пишем любой двучлен с переменными х и у, например 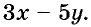
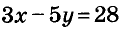
Есть много других линейных уравнений с двумя переменными, имеющих такое же решение (1; -5).
График линейного уравнения с двумя переменными
Рассмотрим уравнение 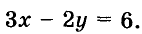
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
💡 Видео
Система неравенств в целых числах | Нестандартные задачи 1Скачать

Уравнение в целых числах | Нестандартные задачи 6Скачать

Как решать неравенства? Часть 1| МатематикаСкачать

Найти все тройки целых чисел, удовлетворяющих неравенствуСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать