Как найти область определения функции иррационального уравнения (7 видео)

Содержание

Иррациональные уравнения. Можно ли писать ОДЗ?
Алгебра
Иррациональные уравнения
Простейшие иррациональные уравнения
Уравнения с двумя квадратными корнями
Введение новых переменных
Замена иррационального уравнения системой
Уравнения с «вложенными» радикалами
Иррациональные неравенства
Методы решения иррациональных уравнений
🎬 Видео

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Иррациональные уравнения. Можно ли писать ОДЗ?

Иррациональными называются уравнения, содержащие знак корня – квадратного, кубического или n-ной степени.

Мы помним из школьной программы: как только в уравнении или неравенстве встретились корни, дроби или логарифмы – пора вспомнить про область допустимых значений (ОДЗ) уравнения или неравенства.

По определению, ОДЗ уравнения (или неравенства) – это пересечение областей определения всех функций, входящих в уравнение или неравенство,

Например, в уравнении присутствует арифметический квадратный корень . Он определен
при .

В 2018-2019 году среди учителей появилось такое мнение, что писать слова «область допустимых значений» уже не модно. И что за это даже могут снизить оценку на экзамене.

Нет, оценку не снизят. И основных понятий школьной математики никто не отменял. Однако есть еще лучший способ оформления решения – в виде цепочки равносильных переходов. Смотрите, как решать и оформлять иррациональные уравнения:

1.Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Выражение под корнем должно быть неотрицательно. И сам корень – величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

Повторим, что решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов. Если вы не очень хорошо понимаете, что такое система уравнений и совокупность уравнений, — повторите эту тему.

В ответ запишем меньший из корней: — 9.

Теперь уравнение, в котором есть ловушка.

2.Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Что получилось у вас? Правильный ответ: . Если у вас получилось – это был посторонний корень. Запишите решение в виде цепочки равносильных переходов, как в задаче 1, и вы поймете, что
не может быть корнем этого уравнения.

Запишем решение как цепочку равносильных преобразований. Учитесь читать такую запись и применять ее.

Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю, а другие при этом не теряют смысла.

А теперь сложное уравнение. Как это часто бывает, нас выручит замена переменной.

Причем новая переменная будет не одна, а целых две.

Мы можем, как в задаче 10, возвести обе части уравнения в квадрат. Но после этого придется еще раз возводить в квадрат, а это долгий способ.

Есть короткий путь!

Выразим через и :

и . Это выражения можно приравнять друг к другу.

Решим одно из уравнений. Все равно, какое, — ведь нам надо найти .

Ответ: . Заметим, что является также и корнем уравнения

Видео:Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Алгебра

План урока:

Видео:9 класс, 15 урок, Определение числовой функции. Область определения, область значения функцииСкачать

Иррациональные уравнения

Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.

Приведем примеры иррациональных ур-ний:

Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести

Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.

Видео:Как найти область определения функции? #shortsСкачать

Простейшие иррациональные уравнения

Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:

где а – некоторое число (константа), f(x) – рациональное выражение.

Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:

Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии

n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.

Ответ: корней нет.

Пример. Решите ур-ние

Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:

Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).

Пример. Найдите решение ур-ния

Решение. Возведем обе части в пятую степень:

х 2 – 14х – 32 = 0

Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:

D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324

Итак, нашли два корня: (– 2) и 16.

Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.

Пример. Решите ур-ние

Решение. Возводим обе части во вторую степень:

х – 2 = х 2 – 8х + 16

D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9

Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):

при х = 3 х – 4 = 3 – 4 = – 1

при х = 6 6 – 4 = 6 – 4 = 2

Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.

Пример. Решите ур-ние

Решение. Здесь используется кубический корень, а потому возведем обе части в куб:

3х 2 + 6х – 25 = (1 – х) 3

3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3

Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:

Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.

Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:

при х = 2 1 – х = 1 – 2 = – 1

Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:

Видео:Область определения (корня) функции #2. Алгебра 10 класс.Скачать

Уравнения с двумя квадратными корнями

Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.

Пример. Решите ур-ние

Решение. Перенесем вправо один из корней:

Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:

Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:

Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:

(2х – 4) 2 = 13 – 3х

4х 2 – 16х + 16 = 13 – 3х

4х 2 – 13х + 3 = 0

D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121

Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:

Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3

На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.

Видео:Иррациональные уравнения и их системы. 11 класс.Скачать

Введение новых переменных

Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние

Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.

Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:

х 1/2 – 10х 1/4 + 9 = 0

Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид

Это квадратное ур-ние. Найдем его корни:

D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64

Получили два значения t. Произведем обратную замену:

х 1/4 = 1 или х 1/4 = 9

Возведем оба ур-ния в четвертую степень:

(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4

х = 1 или х = 6561

Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:

В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.

Пример. Решите ур-ние

х 1/3 + 5х 1/6 – 24 = 0

Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:

Его корни вычислим через дискриминант:

D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121

Далее проводим обратную заменуx 1/6 = t:

х 1/6 = – 8 или х 1/6 = 3

Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.

Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

Замена иррационального уравнения системой

Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.

Пример. Решите ур-ние

Решение. Заменим первый корень буквой u, а второй – буквой v:

Исходное ур-ние примет вид

Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:

Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:

Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:

(х + 6) + (11 – х) = u 3 + v 2

из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:

17 = u 3 + (5 – u) 2

17 = u 3 + u 2 – 10u + 25

u 3 + u 2 – 10u + 8 = 0

Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа

подставим полученные значения в (4):

x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3

x + 6 = 1 или х + 6 = 8 или х + 6 = – 64

х = – 5 или х = 2 или х = – 70

Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим

Корень подошел. Проверяем следующее число, х = 2:

Корень снова оказался верным. Осталась последняя проверка, для х = – 70:

Итак, все три числа прошли проверку.

Видео:Область определения функции - 25 функций в одном видеоСкачать

Уравнения с «вложенными» радикалами

Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:

При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:

Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:

Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:

Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:

Возводим в квадрат и получаем:

х 2 + 40 = (х + 4) 2

х 2 + 40 = х 2 + 8х + 16

И снова нелишней будет проверка полученного корня:

Видео:ОДЗ иррациональных выраженийСкачать

Иррациональные неравенства

По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:

Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.

Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида

Может быть справедливым только тогда, когда

То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во

при четном n можно заменить системой нер-в

Пример. При каких значениях x справедливо нер-во

Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:

х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)

Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во

чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.

Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.

Пример. Найдите решение нер-ва

Решение. Всё очень просто – надо всего лишь возвести обе части в куб:

x 2 – 7x– 8 2 – 7x– 8 = 0

D = b 2 – 4ac = (– 7) 2 – 4•1•(– 8) = 49 + 32 = 81

Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:

Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.

Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.

Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид

Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.

Пример. Решите нер-во

Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):

И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:

D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9

Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.

стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:

f(x) > 0 (подкоренное выражение не может быть отрицательным);

g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).

Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.

Пример. Решите нер-во

Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим

х 2 – 10х + 21 > 0(1)

Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:

Во-вторых, выражение 4 – х не может быть отрицательным:

Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):

Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:

Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:

Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:

Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:

Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).

Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3

Видео:№354 Найти область определения логарифмической функции (АНА 10-11 кл., Алимов Ш.А.)Скачать

Методы решения иррациональных уравнений

Методы решения иррациональных уравнений.

Цели:

Образовательная –познакомить учащихся с нестандартными методами решения иррациональных уравнений; систематизировать знания учащихся о методах решения иррациональных уравнений, способствовать формированию умений классифицировать иррациональные уравнения по методам решений, научить применять эти методы, выбирать рациональный путь решения. Развивающая –способствовать развитию математического кругозора, логического мышления. Воспитательная – содействовать воспитанию интереса к иррациональным уравнениям, воспитывать чувство коллективизма, самоконтроля, ответственности.

1. Повторить определение и основные методы решения иррациональных уравнений;

2. Продемонстрировать нестандартные методы решения иррациональных уравнений; формировать умение выбирать рациональные пути решения;

3. Освоение всеми учащимися алгоритмов решения иррациональных уравнений, закрепление теоретических знаний при решении конкретных примеров;

4. Развитие у учащихся логического мышления в процессе поиска рациональных методов и алгоритмов решения;

5. Развитие культуры научных и учебных взаимоотношений между учениками и между учениками и учителем; воспитание навыков совместного решения задач.

Тип урока:

Методы обучения:

Информационно- иллюстративный; репродуктивный; проблемный диалог; частично-поисковый; системные обобщения.

Формы организации учебной деятельности:

Фронтальная, групповая, самопроверка, взаимопроверка, коллективные способы обучения.

Оборудование урока: компьютер, проектор, карточки с заданием, лист учета знаний.

Продолжительность занятия: 2 урока по 45 минут.

План урока:

I. Организационный момент. Постановка цели, мотивация.

II. Актуализация опорных знаний, проверка домашней работы.

III. Изучение нового материала.

IV. Закрепление изученного материала на данном уроке и ранее пройденного, связанного с новым.

V. Подведение итогов и результатов урока. Рефлексия.

VI. Задание на дом.

I Организационный момент. Постановка цели, мотивация.

II Актуализация опорных знаний проводится в форме беседы по лекционному материалу по данной теме с использованием компьютерной презентации. Проверка домашнего задания.

· Определение иррационального уравнения.

Уравнение, содержащее переменные под знаком корня или дробной степени, называется иррациональным.

Назовите иррациональные уравнения:

· Что значит решить иррациональное уравнение?

Это значит найти все такие значения переменной, при которых уравнение превращается в верное равенство, либо доказать, что таких значений не существует.

· Основные методы решения иррациональных уравнений.

1. Уединение радикала. Возведение в степень.

a) При решении иррационального уравнения с радикалом четной степени возможны два пути:

1) использование равносильных преобразований

для уравнения вида

2) после возведения в степень выполнение проверки, так как возможно появление посторонних корней

b) При решении иррационального уравнения с радикалом нечетной степени возведение в нечетную степень правой и левой части уравнения всегда приводит к равносильному уравнению и потеря корней или их приобретения происходить не может.

Пример 1:

Пример 2:

Пример 3:

Проверка: x=2 x=5

— посторонний корень

Если радикалов несколько, то уравнение возводить в степень приходится возводить неоднократно.

Пример 4:

Проверка показывает, что оба корня подходят.

Ответ:

2. Метод введения вспомогательного неизвестного или “метод замены

Пример 5:

Сделаем замену причём тогда

не удовлетворяет условию

Возвращаемся к замене:

Проверка показывает, что оба корня подходят.

Иногда удобно ввести не одну, а несколько переменных.

Пример 6: .

Заметим, что знаки х под радикалом различные. Введем обозначение

, .

Тогда,

Выполним почленное сложение обеих частей уравнения .

Имеем систему уравнений

Т. к. а + в = 4, то

Значит: 9 – x = 8 , х = 1.

3. Метод разложения на множители или расщепления.

· Произведение равно нулю тогда и только тогда, когда хотя бы один из входящих в него сомножителей равен нулю, а остальные при этом имеют смысл.

Пример 7:

III Изучение нового материала.

Нестандартные методы решения иррациональных уравнений.

4. Умножение на сопряжённое выражение.

5. Переход к модулю.

6. Использование свойств функции:

§ Область определения функции (ОДЗ)

§ Область значения функции

§ Свойство ограниченности функции (метод оценок)

§ Использование суперпозиций функций

· Умножение на сопряжённое выражение.

Воспользуемся формулой

Пример 8:

Умножим обе части уравнения на сопряжённое выражение:

Проверка показывает, что число является корнем.

Ответ:

· Переход к модулю.

Для этого метода воспользуемся тождеством:

Пример 9:

§ Если , то , тогда

тогда

§ Если , тогда ,а

§ Если , тогда , а

· Использование свойств функции:

§ Область определения функции (ОДЗ)

Иногда нахождение области определения функций, входящих в уравнение, существенно облегчает его решение.

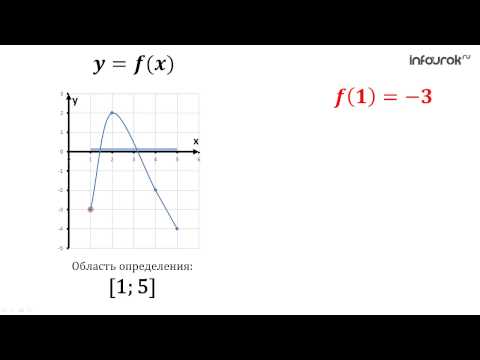
Пример 10:

ОДЗ: ОДЗ: x=0 и x=1

Проверка показывает, что только x=1 является корнем.

Ответ:

Пример 11:

, тогда

Тогда невозможно.

Ответ: корней нет.

§ Область значений функции

Пример 12:

Данное уравнение не имеет решений, так как его левая часть — функция может принимать только неотрицательные значения.

Ответ: корней нет

Пример 13:

Учитывая то, что левая часть уравнения – функция может принимать только неотрицательные значения, решим неравенство:

неравенство решений не имеет, тогда и исходное уравнение тоже.

Ответ: корней нет

§ Свойство ограниченности функции (метод оценок)

· Если и , то

Пример 14:

Заметим, что , т. е. , а

Проверка показывает, что это значение является и корнем второго уравнения.

Ответ:

· Пусть — функция, возрастающая (убывающая) на некотором промежутке I. Тогда уравнение имеет на промежутке I не более одного корня.

· Пусть — функция, возрастающая на некотором промежутке I , а функция — убывающая на этом промежутке. Тогда уравнение имеет на промежутке I. не более одного корня

Пример 15: .

Рассмотрим функции и .

монотонно возрастает, а — убывает, следовательно, уравнение имеет не более одного корня.

Значение корня легко найти подбором:

Ответ:

Пример 16:

Функция возрастает на своей области определения, как сумма двух возрастающих функций, следовательно, уравнение имеет не более одного корня. Так как , то — единственный корень .