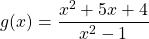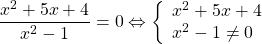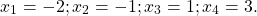Как найти нули тригонометрической функции по уравнению

Ключевые слова: тригонометрия, функция, синус, косинус, тангенс, котангенс, область определения, множество значений

D(tg) = R, $$x ne frac+pi n$$

Видео:Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.Скачать

Нули функции

Что такое нули функции? Как определить нули функции аналитически и по графику?

Нули функции — это значения аргумента, при которых функция равна нулю.

Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.

Если уравнение не имеет корней, нулей у функции нет.

1) Найти нули линейной функции y=3x+15.

Чтобы найти нули функции, решим уравнение 3x+15 =0.

Таким образом, нуль функции y=3x+15 — x= -5 .

2) Найти нули квадратичной функции f(x)=x²-7x+12.

Для нахождения нулей функции решим квадратное уравнение

Его корни x1=3 и x2=4 являются нулями данной функции.

3)Найти нули функции

Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0, x² ≠ 1,x ≠±1. То есть область определения данной функции (ОДЗ)

Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.

Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.

Если график не пересекает ось Ox, функция не имеет нулей.

функция, график которой изображен на рисунке,имеет четыре нуля —

В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.

Видео:Нули функции / Где они? / как их найти / Все про функции (урок 6)Скачать

Геометрия. Урок 1. Тригонометрия

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Видео:ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 11 класс графики тригонометрических функцийСкачать

Тригонометрия в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

Видео:График функции y=sinx и ее свойства. 10 класс.Скачать

Тригонометрия: Тригонометрический круг

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .

Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .

Рассмотрим прямоугольный треугольник A O B :

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .

Координата по оси x – косинус угла , координата по оси y – синус угла .

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .

Видео:10 класс, 16 урок, Функции y=sinx, y=cosx, их свойства и графикиСкачать

Основное тригонометрическое тождество

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

Видео:Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Тригонометрия: Таблица значений тригонометрических функций

Видео:Свойства функции. Нули функции. Практическая часть. 10 класс.Скачать

Тригонометрия: градусы и радианы

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Видео:Найти нули функции. 9 класс. АлгебраСкачать

Тригонометрия: Формулы приведения

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Видео:Функция. Множество значений функции. Практическая часть. 10 класс.Скачать

Тригонометрия: Теорема синусов

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Тригонометрия: Расширенная теорема синусов

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Видео:Свойства функции. Нули функции, экстремумы. 10 класс.Скачать

Тригонометрия: Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Видео:Область определения тригонометрических функцийСкачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с тригонометрией.

Видео:Тригонометрические функции, y=tgx и y=ctgx, их свойства и графики. 10 класс.Скачать

Тригонометрия: Тригонометрические уравнения

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

🔥 Видео

Свойства функции. Промежутки возрастания и убывания функции. 10 класс.Скачать

Обратные тригонометрические функции, y=arcsinx и y=arccosx, их свойства и графики. 10 класс.Скачать

Множество значений тригонометрических функцийСкачать

Тригонометрические функции и их знакиСкачать

Свойства функции. Промежутки знакопостоянства. 10 класс.Скачать

Область определения функции - 25 функций в одном видеоСкачать

Область определения и область значений тригонометрических функций -1 частьСкачать