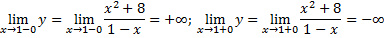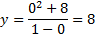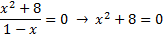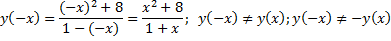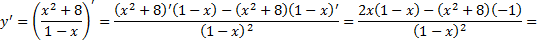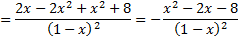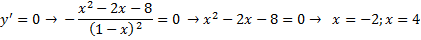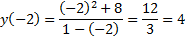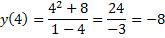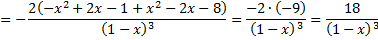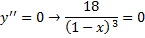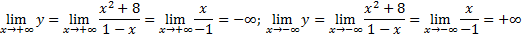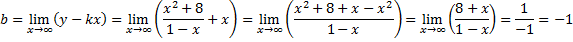Как найти нули функции по уравнению производной

теория по математике 📈 функции

Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.

На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.

Остановимся подробнее на свойствах функций.

Нули функции

Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

График функции у=k/x выглядит следующим образом: 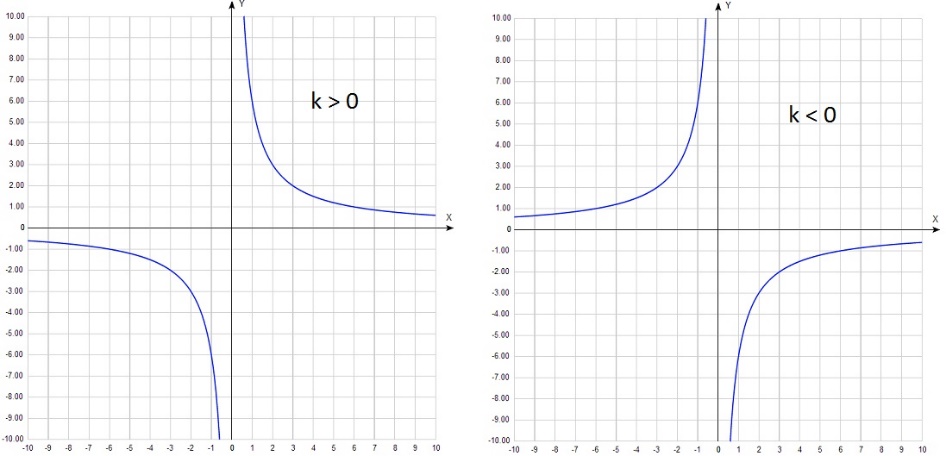По данному рисунку видно, что нулей функции не существует. Как найти нули функции?

1. Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
2. Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.

Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):

а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22

Находим х, разделив 22 на 11: х=22:11

Таким образом, мы нашли нуль функции: х=2

б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.

в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.

Пример №2. Найти нули функции у=f(x) по заданному графику.

Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.

Промежутки знакопостоянства

Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.

Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.

На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.

Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.

Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).

Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.

Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.

Возрастание и убывание функции

Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.

На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.

Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.

Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Видео:Свойства функции. Нули функции. Практическая часть. 10 класс.Скачать

Применение производной. Построение графиков с применением производных

Математика берет свои истоки со времен Античности. Благодаря ней архитектура, строительство и военное дело дали новый виток развития, достижения, которые были получены с помощью математики, привели к движению прогресса. И по сей день математика остается главной наукой, которая встречается во всех остальных отраслях.

Чтобы быть образованными, дети с первого класса начинают постепенно вливаться в эту среду. Очень важно разбираться в математике, так как она, в той или иной степени, встречается каждому человеку на протяжении всей его жизни. В этой статье будет разобран один из ключевых элементов — нахождение и применение производных. Не всякий человек может представить, насколько широко используется это понятие. Рассмотрим более 10 применений производных в определенных областях или науках.

Видео:Нули функции / Где они? / как их найти / Все про функции (урок 6)Скачать

Применение производной к исследованию функции

Производная — это такой предел отношения приращения функции к увеличению ее аргумента, когда показатель аргумента стремится к нулю. Производная — незаменимая вещь при исследовании функции. Например, с помощью нее можно определить возрастание и убывание последней, экстремумы, выпуклости и вогнутости. Дифференциальные исчисления входят в обязательную программу обучения студентов 1 и 2 курса математических вузов.

Видео:Свойства функции. Нули функции, экстремумы. 10 класс.Скачать

Область определения и нули функции

Первый этап любого исследования графика начинается с выяснения области определения, в более редких случаях — значения. Область определения задается по оси абсциссы, если говорить другими словами, то это числовые значения на оси OX. Часто область определения уже задана, но если она не задана, то следует оценить значение аргумента х. Допустим, если при каком-то значениях аргумента функция не имеет смысла, то этот аргумент исключается из области определения.

Нули функции находятся простым способом: функцию f(x) следует приравнивнять к нулю и решить полученное уравнение относительно одной переменной x. Полученные корни уравнения являются нулями функции, то есть в этих x функция равна 0.

Видео:Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Возрастание и убывание

Применение производной для исследования функций на монотонность может рассматриваться с двух позиций. Монотонная функция — это категория, которая имеет только положительные значения производной, либо только отрицательные. Простыми словами — функция только возрастает или только убывает на всем исследуемом промежутке:

1. Параметр возрастания. Функция f(x) будет возрастать, если производная f`(x) больше нуля.
2. Параметр убывания. Функция f(x) будет убывать, если производная f`(x) меньше нуля.

Видео:АЛГЕБРА С НУЛЯ — Что такое Производная?Скачать

Касательная и угловой коэффициент

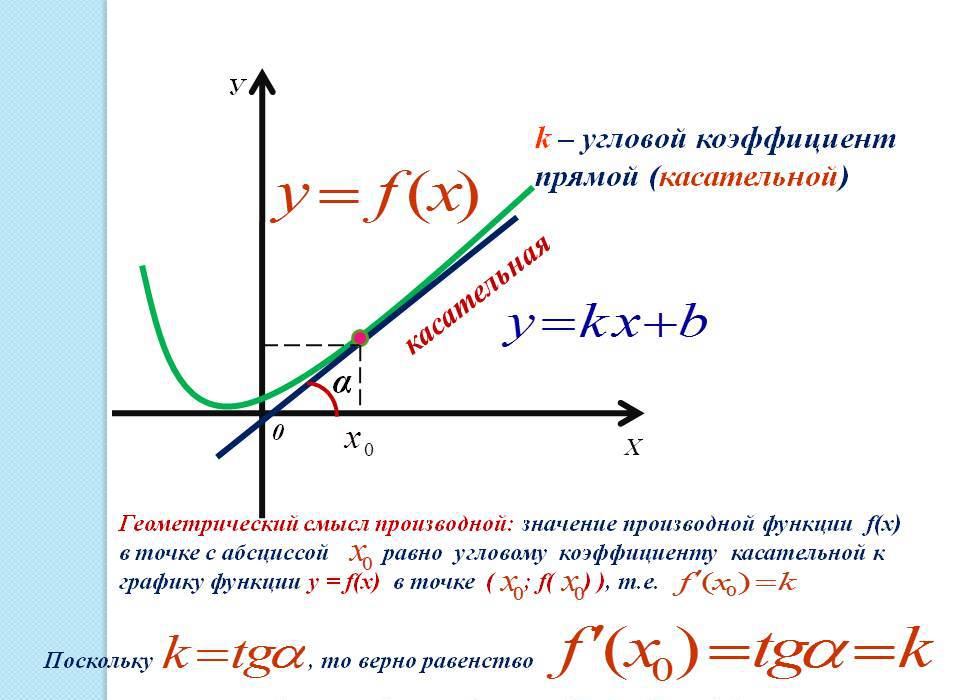
Применение производной к исследованию функции определяется еще и касательной (прямой, направленной под углом) к графику функции в данной точке. Касательная в точке (x₀) — прямая, которая проходит через точку и принадлежит функции, координаты которой (x₀, f(x₀)), и имеющая угловой коэффициент f`(x₀).

y = f(x₀) + f`(x₀)(x — x₀) — уравнение касательной к данной точке графика функции.

Геометрический смысл производной: производная функции f(x) равняется угловому коэффициенту образованной касательной к графику этой функции в данной точке x. Угловой коэффициент, в свою очередь, равняется тангенсу угла наклона касательной к оси ОХ (абсцисс) в положительном направлении. Это следствие является основополагающим к применению производной к графику функции.

Видео:Математика Без Ху!ни. Производная сложной функции.Скачать

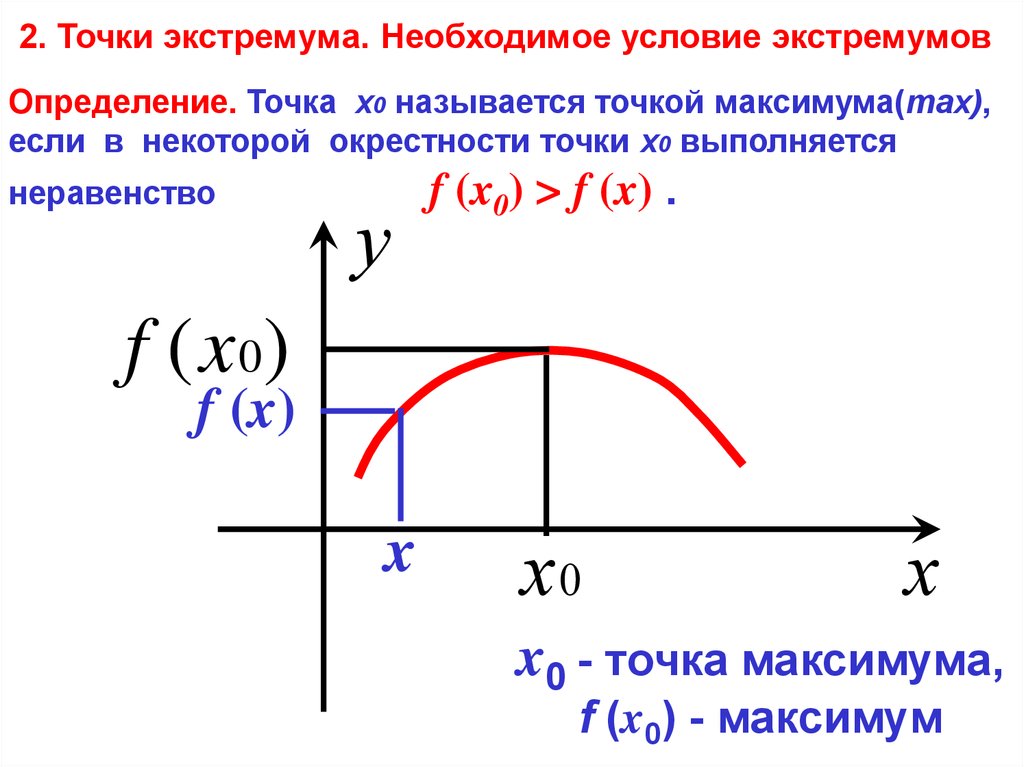
Точки экстремума

Применение производной к исследованию включает в себя нахождение точек максимума и минимума.

Для того чтобы найти и определить точки минимума и максимума, необходимо:

• Отыскать производную функции f(x).
• Приравнять полученное уравнение к нулю.
• Найти корни уравнения.
• Определить точки максимума и минимума.

Чтобы найти экстремумы функции:

• Отыскать точки минимума и максимума по способу выше.
• Подставить эти точки в первоначальное уравнение и высчитать y_наиб. и y_наим.

Точка максимума функции — это наибольшее значение функции f(x) на промежутке, другими словами x_наиб.

Точка минимума функции — это наименьшее значение функции f(x) на промежутке, другими словами x_наим.

Точки экстремума — то же самое, что и точки максимума и минимума, а экстремум функции (y_{наиб. и} у_наим) — значения функций, которые соответствуют точкам экстремума.

Видео:Свойства функции. Промежутки возрастания и убывания функции. 10 класс.Скачать

Выпуклости и вогнутости

Определить выпуклость и вогнутость можно, прибегая к применению производной для построения графиков:

• Функция f(x), исследуемая на промежутке (a, b), является вогнутой, если функция расположена ниже всех своих касательных, находящихся внутри этого интервала.
• Функция f(x), исследуемая на промежутке (a, b), является выпуклой, если функция расположена выше всех своих касательных, находящихся внутри этого интервала.

Точка, которая разделяет выпуклость и вогнутость, называется точкой перегиба функции.

Чтобы найти точки перегиба:

• Найти критические точки второго рода (вторую производную).
• Точками перегиба являются те критические точки, которые разделяют два противоположенных знака.
• Вычисление значений функций в точках перегиба функции.

Видео:Область определения функции - 25 функций в одном видеоСкачать

Частные производные

Применение производных такого типа есть в задачах, где используется больше одной неизвестной переменной. Чаще всего такие производные встречаются при построении графика функции, если быть точнее, то поверхности в пространстве, где вместо двух осей — три, следовательно, три величины (две переменные и одна постоянная).

Основное правило при вычислении частных производных — выбираем одну переменную, а остальные рассматриваем как постоянные. Следовательно, при вычислении частной производной постоянная величина становится как-будто числовым значением (во многих таблицах производных они обозначаются как C = const). Смысл такой производной — это скорость изменения функции z = f(x, y) по оси OX и OY, то есть характеризует крутизну впадин и выпуклостей построенной поверхности.

Видео:Урок 13. Применение производной к построению графиков функций. Алгебра 11 классСкачать

Производная в физике

Применение производной в физике имеет широкое распространение и значение. Физический смысл: производная пути по времени — скорость, а ускорение — производная скорости по времени. Из физического смысла можно провести множество ответвлений в различные разделы физики, при этом полностью сохраняя смысл производной.

С помощью применения производной находятся такие величины:

• Скорость в кинематике, где вычисляется производная от пройденного пути. Если находится вторая производная от пути или первая производная от скорости, то находится ускорение тела. Помимо этого, возможно нахождение мгновенной скорости материальной точки, однако для этого необходимо знать приращение ∆t и ∆r.
• В электродинамике: вычисление мгновенной силы переменного тока, а также ЭДС электромагнитной индукции. Вычисляя производную, можно найти максимальную мощность. Производная от количества электрического заряда — сила тока в проводнике.

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Производная в химии и биологии

Химия: производная используется для определения скорости протекания химической реакции. Химический смысл производной: функция p = p(t), в данном случае p — количество вещества, которое вступает в химическую реакцию во времени t. ∆t — приращение времени, ∆p — приращение количества вещества. Предел отношения ∆p к ∆t, при котором ∆t стремится к нулю, называется скоростью протекания химической реакции. Среднее значение химической реакции — отношение ∆p/∆t. При определении скорости необходимо точно знать все необходимые параметры, условия, знать агрегатное состояние вещества и среду протекания. Это довольно большой аспект в химии, который широко применяется в различных отраслях и деятельности человека.

Биология: понятие производной используют при вычислении средней скорости размножения. Биологический смысл: имеем функцию y = x(t). ∆t — приращение по времени. Тогда с помощью некоторых преобразований получаем функцию y`= P(t) = x`(t) — активность жизнедеятельности популяции времени t (средняя скорость размножения). Такое применение производной позволяет вести статистику, отслеживать темпы размножения и так далее.

Видео:7.5 ЧАСОВ МАТАНА!!! ПОДАРОК ВСЕМ СТУДЕНТАМ ДЛЯ ПОДГОТОВКИ К ЗАЧЁТАМ И ЭКЗАМЕНАМ ОТ ЁЖИКА В МАТАНЕ!!!Скачать

Производная в географии и экономике

Производная позволяет географам решать такие задачи, как нахождение численности населения, вычислять значения в сейсмографии, рассчитать радиоактивность ядерно-геофизических показателей, вычислить интерполяцию.

В экономике важную часть расчетов занимает дифференциальное исчисление и вычисление производной. В первую очередь это позволяет определить пределы необходимых экономических величин. Например, наибольшую и наименьшую производительность труда, издержки, прибыль. В основном эти величины рассчитываются по графикам функций, где находят экстремумы, определяют монотонность функции на нужном участке.

Видео:Для 1 курса. Исследование функций и построение графиков.Скачать

Заключение

Роль данного дифференциального исчисления задействована, как было отмечено в статье, в различных научных структурах. Применение производных функций — важный элемент в практической части науки и производства. Не зря нас в старшей школе и университете учили строить сложные графики, исследовать и работать над функциями. Как видим, без производных и дифференциальных исчислений невозможно было бы рассчитать жизненно важные показатели и величины. Человечество научилось моделировать различные процессы и исследовать их, решать сложные математические задачи. Действительно, математика — царица всех наук, потому что эта наука лежит в основе всех других естественных и технических дисциплин.

Видео:Найти нули функции. 9 класс. АлгебраСкачать

Исследование функции и построение графика

На этой странице мы постарались собрать для вас наиболее полную информацию об исследовании функции. Больше не надо гуглить! Просто читайте, изучайте, скачивайте, переходите по отобранным ссылкам.

Что будет дальше?

Видео:Математика без Ху!ни. Исследование функции, график. Первая, вторая производная, асимптоты.Скачать

Общая схема исследования

Для чего нужно это исследование, спросите вы, если есть множество сервисов, которые построят график онлайн для самых замудренных функций? Для того, чтобы узнать свойства и особенности данной функции: как ведет себя на бесконечности, насколько быстро меняет знак, как плавно или резко возрастает или убывает, куда направлены «горбы» выпуклости, где не определены значения и т.п.

А уже на основании этих «особенностей» и строится макет графика — картинка, которая на самом-то деле вторична (хотя в учебных целях важна и подтверждает правильность вашего решения).

Начнем, конечно же, с плана. Исследование функции — объемная задача (пожалуй, самая объемная из традиционного курса высшей математики, обычно от 2 до 4 страниц с учетом чертежа), поэтому, чтобы не забыть, что в каком порядке делать, следуем пунктам, описанным ниже.

Алгоритм

1. Найти область определения. Выделить особые точки (точки разрыва).
2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
3. Найти точки пересечения с осями координат.
4. Установить, является ли функция чётной или нечётной.
5. Определить, является ли функция периодической или нет (только для тригонометрических функций).
6. Найти точки экстремума и интервалы монотонности.
7. Найти точки перегиба и интервалы выпуклости-вогнутости.
8. Найти наклонные асимптоты. Исследовать поведение на бесконечности.
9. Выбрать дополнительные точки и вычислить их координаты.
10. Построить график и асимптоты.

В разных источниках (учебниках, методичках, лекциях вашего преподавателя) список может иметь отличный от данного вид: некоторые пункты меняются местами, объединяются с другими, сокращаются или убираются. Учитывайте требования/предпочтения вашего учителя при оформлении решения.

Схема исследования в формате pdf: скачать.

Видео:Производная функции. 10 класс.Скачать

Полный пример решения онлайн

Провести полное исследование и построить график функции $$ y(x)=frac. $$

1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя. $$1-x=0, quad Rightarrow quad x=1.$$ Исключаем единственную точку $x=1$ из области определения функции и получаем: $$ D(y)=(-infty; 1) cup (1;+infty). $$

2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:

Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ — вертикальная асимптота.

3) Определим точки пересечения графика функции с осями координат.

Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:

Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.

Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:

Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.

Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x in (-infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x in (1; +infty)$ функция $ylt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).

4) Функция не является ни четной, ни нечетной, так как:

5) Исследуем функцию на периодичность. Функция не является периодической, так как представляет собой дробно-рациональную функцию.

6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:

Приравняем первую производную к нулю и найдем стационарные точки (в которых $y’=0$):

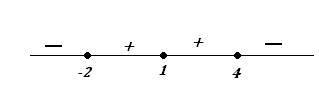
Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:

При $x in (-infty; -2), (4;+infty)$ производная $y’ lt 0$, поэтому функция убывает на данных промежутках.

При $x in (-2; 1), (1;4)$ производная $y’ >0$, функция возрастает на данных промежутках.

При этом $x=-2$ — точка локального минимума (функция убывает, а потом возрастает), $x=4$ — точка локального максимума (функция возрастает, а потом убывает).

Найдем значения функции в этих точках:

Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.

7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:

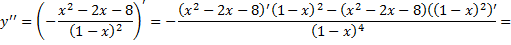
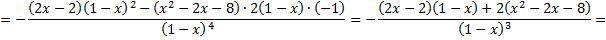
Приравняем вторую производную к нулю:

Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x in (-infty; 1)$ выполняется $y» gt 0$, то есть функция вогнутая, когда $x in (1;+infty)$ выполняется $y» lt 0$, то есть функция выпуклая.

8) Исследуем поведение функции на бесконечности, то есть при .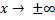

Так как пределы бесконечны, горизонтальных асимптот нет.

Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:

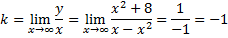
Получили, у что функции есть одна наклонная асимптота $y=-x-1$.

9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.

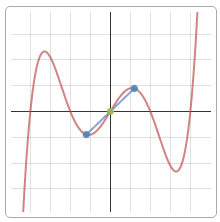
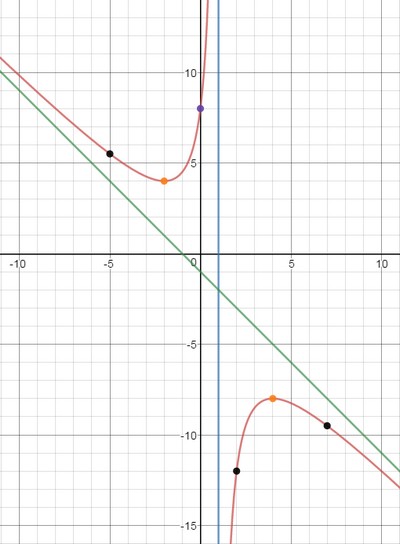
10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):

Видео:АЛГЕБРА С НУЛЯ — Точки Экстремума ФункцииСкачать

Примеры решений по исследованию функции

Разные функции (многочлены, логарифмы, дроби) имеют свои особенности при исследовании (разрывы, асимптоты, количество экстремумов, ограниченная область определения), поэтому здесь мы пострались собрать примеры из контрольных на исследование функций наиболее часто встречающихся типов. Удачи в изучении!

Задача 1. Исследовать функцию методами дифференциального исчисления и построить график.

Задача 2. Исследовать функцию и построить ее график.

Задача 3. Исследовать функцию с помощью производной и построить график.

Задача 4. Провести полное исследование функции и построить график.

Задача 5. Исследовать функцию методом дифференциального исчисления и построить график.

Задача 6. Исследовать функцию на экстремумы, монотонность, выпуклость и построить график.

Задача 7. Проведите исследование функции с построением графика.

Задача 8. Построить график функции $y=y(x)$, заданной параметрически

Задача 9. Исследовать функцию и построить ее график $r=1+tg phi$.

Задача 10. Исследовать функцию и построить ее график $(x^2+y^2)^3=4x^2y^2$.

Задача 11. Провести полное исследование периодической функции $y = cos 3x – 2 sin 6x$ и построить её график.

Задача 12. Провести полное исследование и построить график функции $y=f(x)$ с помощью Excel. Найти наибольшее и наименьшее значения функции на отрезке $[-3; -1]$.

Задача 13. Провести полное исследование и построить график функции.

Видео:10 класс, 44 урок, Применение производной для исследования функций на монотонность и экстремумыСкачать

Как построить график онлайн?

Даже если преподаватель требует вас сдавать задание, написанное от руки, с чертежом на листке в клеточку, вам будет крайне полезно во время решения построить график в специальной программе (или сервисе), чтобы проверить ход решения, сравнить его вид с тем, что получается вручную, возможно, найти ошибки в своих расчетах (когда графики явно ведут себя непохоже).

Ниже вы найдете несколько ссылок на сайты, которые позволяют построить удобно, быстро, красиво и, конечно, бесплатно графики практически любых функций. На самом деле таких сервисов гораздо больше, но стоит ли искать, если выбраны лучшие?

Графический калькулятор Desmos

Desmos.com
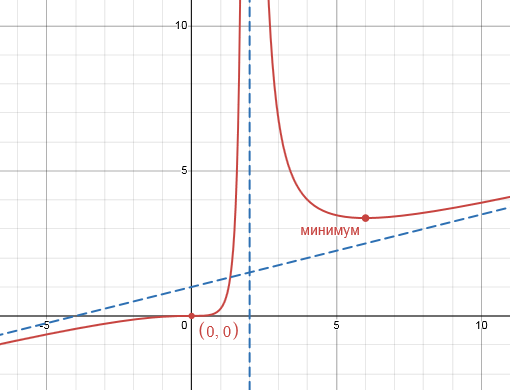
Невероятно гибкий и функциональный графический калькулятор. Интутивно понятно вводятся формулы (прямо на ходу преобразуются), автоматически подбираются масштаб и цвета графика для максимальной наглядности. Например, для функции $y(x)=frac$ буквально за минуту построены основной график и асимптоты, вот что получилось:

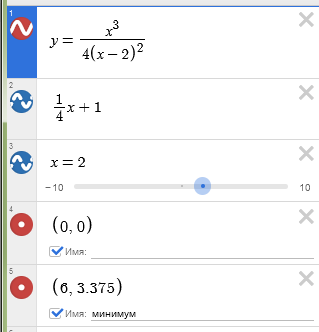
При этом сайт сам пометил важные точки на графике (см. серым): локальный экстремум, пересечение с осями.

Вы можете менять масштаб, цвета, вид линий; добавлять на график точки, линии, кривые, табличные данные и даже анимацию!

Посмотрите, какую красоту Desmos умеет рисовать (точнее, его пользователи):

Сайт для построения графиков y(x).ru

y(x).ru
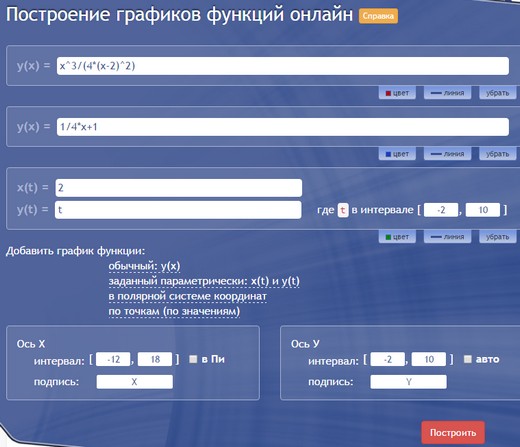
Это уже наш продукт, возможно, не такой красивый и интерактивный, но вполне подходящий для учебных целей. Можно строить онлайн несколько графиков одновременно, при этом выбирать и обычный, и параметрический вид, и даже задание в полярных координатах. Цвет и масштаб можно менять вручную. Вот так вводятся графики:

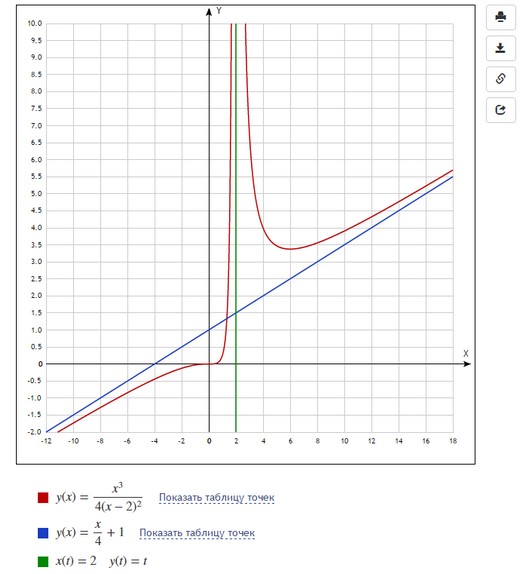
И такой график получается в итоге:

Из минусов можно заметить, что вводить, например, горизонтальные асимптоты не так просто: если в Desmos мы просто написали $x=2$, то здесь пришлось вводить параметрическую функцию $x(t)=2, y(t)=t$. Цвета и масштаб тоже пришлось подбирать вручную (иначе все графики оказались бы красными и мелкими).

Другие сайты

Еще несколько сервисов, которые обладают меньшим удобством/функциональностью, но тоже достойны внимания:

• ru.numberempire.com Можно построить сразу несколько функций, цвета подбираются автоматически, график интерактивный (положение и масштаб меняются мышкой).
• mathsolution.ru Можно строить несколько графиков, выбирая толщину линий и цвет, скрывать/отображать сетку, менять масштаб, сохранять картинки в файл.
• easyto.me При построении нескольких графиков на одном поле предыдущие не редактируются. В остальном функции как у прежних: выбор цвета, толщины линии, масштаба чертежа.
• grafikus.ru Кроме обычных графиков можно также строить трехмерные (3d). Можно построить несколько графиков разного типа (обычный,параметрический, в полярных координатах). Цвет и толщину линии выбрать нельзя. Интерактивности нет

Видео:4. Вычисление производных примеры. Самое начало.Скачать

Больше знаний: теория и практика

Еще немного ссылок для тех, кто хочет углубиться в тему. Первая ссылка на теоретический материал, где вы найдете и подробные примеры, и отсылки к предыдущим разделам теории (а исследовать функцию не зная пределов, производных, понятия непрерывности и т.п. нельзя) с не менее подробным объяснением. Все это сдобрено порцией юмора, отчего очень «съедобно» даже для полного чайника в математике: Исследование функций от Александра Емелина.

Вторая ссылка практическая, для тех, кто хочет научиться строить красивые графики в Desmos.com (см. выше описание): Полная инструкция по работе с Desmos. Эта инструкция довольно старая, с тех пор интерфейс сайта поменялся в лучшую сторону, но основы остались неизменными и помогут быстро разобраться с важными функциями сервиса.

Официальные инструкции, примеры и видео-инструкции на английском можно найти тут: Learn Desmos.

Видео:Промежутки возрастания и убывания функции. 10 класс.Скачать

Решебник

Срочно нужна готовая задача? Более сотни разных функций с полным исследованием уже ждут вас. Подробное решение, быстрая оплата по SMS и низкая цена — около 50 рублей. Может, и ваша задача уже готова? Проверьте!

Полезные видео-ролики

Вебинар по работе с Desmos.com. Это уже полноценный обзор функций сайта, на целых 36 минут. К сожалению, он на английском языке, но базовых знаний языка и внимательности достаточно, чтобы понять большую часть.

Классный старый научно-популярный фильм «Математика. Функции и графики». Объяснения на пальцах в прямом смысле слова самых основ.