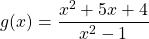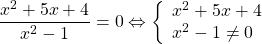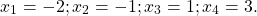Как найти нули функции по уравнению алгебре (4 видео)

Нули функции

Что такое нули функции? Как определить нули функции аналитически и по графику?

Нули функции — это значения аргумента, при которых функция равна нулю.

Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.

Если уравнение не имеет корней, нулей у функции нет.

1) Найти нули линейной функции y=3x+15.

Чтобы найти нули функции, решим уравнение 3x+15 =0.

Таким образом, нуль функции y=3x+15 — x= -5 .

2) Найти нули квадратичной функции f(x)=x²-7x+12.

Для нахождения нулей функции решим квадратное уравнение

Его корни x1=3 и x2=4 являются нулями данной функции.

3)Найти нули функции

Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0, x² ≠ 1,x ≠±1. То есть область определения данной функции (ОДЗ)

Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.

Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.

Если график не пересекает ось Ox, функция не имеет нулей.

функция, график которой изображен на рисунке,имеет четыре нуля —

В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.

Видео:Найти нули функции. 9 класс. АлгебраСкачать

Математика. Нули функции + примеры + инструкция

Нули функции — это значения аргумента, при которых функция равна нулю.

Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.

Если уравнение не имеет корней, нулей у функции нет.

Примеры.

1) Найти нули линейной функции y=3x+15.

Чтобы найти нули функции, решим уравнение 3x+15=0.

Таким образом, нуль функции y=3x+15 — x= -5.

2) Найти нули квадратичной функции f(x)=x²-7x+12.

Для нахождения нулей функции решим квадратное уравнение

Его корни x1=3 и x2=4 являются нулями данной функции.

1. Нуль функции – это такое значение довода х, при котором значение функции равно нулю. Впрочем нулями могут быть лишь те доводы, которые входят в область определения исследуемой функции. То есть в такое уйма значений, для которых функция f(x) имеет толк. 2. Запишите заданную функцию и приравняйте ее к нулю, скажем f(x) = 2х?+5х+2 = 0. Решите получившееся уравнение и обнаружьте его действительные корни. Корни квадратного уравнения вычисляются с поддержкой нахождения дискриминанта. 2х?+5х+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;х1 = (-b+?D)/2*а = (-5+3)/2*2 = -0,5;х2 = (-b-?D)/2*а = (-5-3)/2*2 = -2.Таким образом, в данном случае получены два корня квадратного уравнения, соответствующих доводам начальной функции f(x). 3. Все обнаруженные значения х проверьте на принадлежность к области определения заданной функции. Обнаружьте ООФ, для этого проверьте начальное выражение на наличие корней четной степени вида ?f (х), на присутствие дробей в функции с доводом в знаменателе, на наличие логарифмических либо тригонометрических выражений. 4. Рассматривая функцию с выражением под корнем четной степени, примите за область определения все доводы х, значения которых не обращают подкоренное выражение в негативное число (напротив функция не имеет смысла). Уточните, попадают ли обнаруженные нули функции в определенную область допустимых значений х. 5. Знаменатель дроби не может обращаться в нуль, следственно исключите те доводы х, которые приводят к такому итогу. Для логарифмических величин следует рассматривать лишь те значения довода, при которых само выражение огромнее нуля. Нули функции, обращающие подлогарифмическое выражение в нуль либо негативное число, обязаны быть отброшены из финального итога. Обратите внимание! При нахождение корней уравнения, могут возникнуть лишние корни. Проверить это легко: довольно подставить полученное значение довода в функцию и удостовериться обращается ли функция в нуль. Полезный совет Изредка функция не выражается в очевидном виде через свой довод, тогда легко нужно знать, что представляет собой эта функция. Примером этому может служить уравнение окружности.

Нулями функции называются значение абсциссы, при котором значение функции равно нулю.

Если функция задана своим уравнением, то нулями функции будут решения уравнения . Если задан график функции , то нули функции — это значения , в которых график пересекает ось абсцисс.

Видео:СПОРИМ ты поймешь Математику — Функция и ее свойства, Область определения, Нули ФункцииСкачать

Нули функции онлайн

Одной из задач, возникающих при исследовании функции, является нахождение её нулей — т.е. точек пересения с осью абсцисс. Рассмотрим график некоторой функции :

Нулями функции являются точки в которых, как было сказано выше, график функции пересекает ось абсцисс. Чтобы найти нули функции необходимо и достаточно решить уравнение:

Нулями функции будут корни этого уравнения. Таким образом, нули функции находятся в точках .

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha способен найти нули практически любой, даже очень сложной функции.