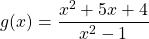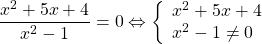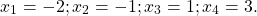Как найти нули функции дробного уравнения

Видео:Свойства функции. Нули функции. Практическая часть. 10 класс.Скачать

Нули функции

Что такое нули функции? Как определить нули функции аналитически и по графику?

Нули функции — это значения аргумента, при которых функция равна нулю.

Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.

Если уравнение не имеет корней, нулей у функции нет.

1) Найти нули линейной функции y=3x+15.

Чтобы найти нули функции, решим уравнение 3x+15 =0.

Таким образом, нуль функции y=3x+15 — x= -5 .

2) Найти нули квадратичной функции f(x)=x²-7x+12.

Для нахождения нулей функции решим квадратное уравнение

Его корни x1=3 и x2=4 являются нулями данной функции.

3)Найти нули функции

Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0, x² ≠ 1,x ≠±1. То есть область определения данной функции (ОДЗ)

Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.

Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.

Если график не пересекает ось Ox, функция не имеет нулей.

функция, график которой изображен на рисунке,имеет четыре нуля —

В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.

Видео:Найти нули функции. 9 класс. АлгебраСкачать

Как найти нули функции по уравнению с дробью?

Алгебра | 5 — 9 классы

Как найти нули функции по уравнению с дробью?

У = дробь в числителе х ^ 2 — 6х + 5 ; в знаменателе х — 5 Объясните пожалуйста!

Ответ : решение представлено на фотоОбъяснение :

Видео:Нули функции / Где они? / как их найти / Все про функции (урок 6)Скачать

Знаменатель несократимой дроби больше ее числителя на 5?

Знаменатель несократимой дроби больше ее числителя на 5.

Если числители дроби увеличить на 2, а ее знаменатель уменьшить на 2 то полученая дробь будет больше на 18 / 35 больше данной дроби.

Найти данную дробь.

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Прочитайте задачу «Знаменатель обыкновенной дроби на 5 больше её числителя?

Прочитайте задачу «Знаменатель обыкновенной дроби на 5 больше её числителя.

Если из числителя вычесть 1, а из знаменателя вычесть 3, то дробь увеличится на 1 / 18.

Чему равен числитель этой дроби?

«. Пусть x — числитель данной дроби, какое уравнение позволяет найти x?

Видео:НУЛИ ФУНКЦИЙ #shorts #математика #егэ #огэ #профильныйегэСкачать

Как приравнять к нулю?

Как приравнять к нулю?

Дробь : в числителе 2х3 — 2 в знаменателе х2 и всё это равно нулю.

Видео:Свойства функции. Нули функции, экстремумы. 10 класс.Скачать

Числитель обыкновенной дроби на 7 меньше его знаменателя?

Числитель обыкновенной дроби на 7 меньше его знаменателя.

Если числитель этой дроби уменьшить на 1 , а знаменатель увеличить на 4 , то дробь уменьшится на 1 / 6 (одну шестую).

Найти данную дробь

Задача решается через «пусть» и уравнение!

Видео:Вариант 28, № 5. Нули квадратичной функции. Пример 4Скачать

Числитель обыкновенной дроби на 7 меньше его знаменателя?

Числитель обыкновенной дроби на 7 меньше его знаменателя.

Если числитель этой дроби уменьшить на 1 , а знаменатель увеличить на 4 , то дробь уменьшится на 1 / 6 (одну шестую).

Найти данную дробь

помогите решить пожалуйста!

Задача решается через «пусть» и уравнение.

Видео:Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Найти область определения функции y = дробь числитель 4 + х знаменатель х — 5?

Найти область определения функции y = дробь числитель 4 + х знаменатель х — 5.

Видео:Как решать уравнения с дробью? #shortsСкачать

Числитель некоторой обыкновенной дроби на 11 больше знаменателя?

Числитель некоторой обыкновенной дроби на 11 больше знаменателя.

Если к числителю дроби прибавить 5, а к знаменателю 12, то получится дробь, втрое меньше исходной.

Найти эту дробь.

Видео:Дробно-линейная функция. 10 класс.Скачать

Сумма числителя и знаменателя некоторой дроби равна 13?

Сумма числителя и знаменателя некоторой дроби равна 13.

Найти эту дробь, если числитель меньше знаменателя на 3.

Видео:СПОРИМ ты поймешь Математику — Функция и ее свойства, Область определения, Нули ФункцииСкачать

Числитель обыкновенной дроби на 7 меньше его знаменателя?

Числитель обыкновенной дроби на 7 меньше его знаменателя.

Если числитель этой дроби уменьшить на 1 , а знаменатель увеличить на 4 , то дробь уменьшится на 1 / 6 (одну шестую).

Найти данную дробь.

Задача решается через «пусть» и уравнение))

Видео:40 Алгебра 9 класс Найдите нули функции если они существуютСкачать

Числитель дроби на 12 меньше знаменателя ?

Числитель дроби на 12 меньше знаменателя .

Если к числителю добавить 29, а из знаменателя вычесть 7, то получится дробь обратная данной .

Найти эту дробь.

На странице вопроса Как найти нули функции по уравнению с дробью? из категории Алгебра вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

1. На калькуляторе √(7) + 2 × √(10) = 8, 9703066314 Ответ : 8, 97.

Видео:Квадратичная функция. Вершина параболы и нули функции. 8 класс.Скачать

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
2. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Видео:Как найти область определения функции? #shortsСкачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

• Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
• Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Видео:Математика это не ИсламСкачать

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Видео:17.3 Найдите нули функции. РешениеСкачать

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

• если значение переменной обращает знаменатель в 0, значит это неверное значение;
• делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

1. Область допустимых значений: х ≠ −2.
2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

🌟 Видео

Алгебра 9 класс (Урок№3 - Свойства функций)Скачать