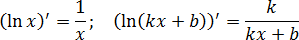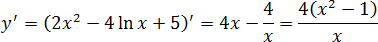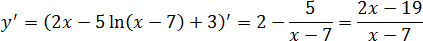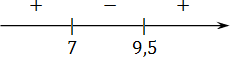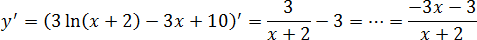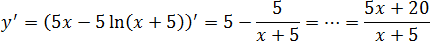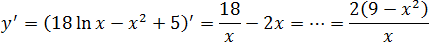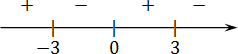Как найти наименьшее значение функции по уравнению с натуральным логарифмом (4 видео)

Специфика работы с логарифмами в задаче B15

22 февраля 2012

Вообще говоря, для решения задачи B15 с логарифмом надо знать две формулы:

Первая формула — классическая производная натурального логарифма, вторая — производная сложной функции. Обратите внимание: в числителе стоит это не опечатка.

Добавьте к этим формулам стандартные правила вычисления производных — и задача B15 решена:

( f ± g ) ’ = f ’ ± g ’;
( c · f ) ’ = c · f ’, c ∈ R.

В настоящих задачах логарифмы никогда не встречаются сами по себе. Поэтому обязательно приводите всю производную к общему знаменателю. Почему это важно, узнаете из примеров.

Задача. Найдите наименьшее значение функции на отрезке [0,5; 4]:

y = 2 x 2 − 4 ln x + 5

Выясняем, когда производная равна к нулю. Дробь равна нулю, когда ее числитель равен нулю. Имеем:

4( x 2 − 1) = 0;
x 2 = 1;
x = ±1.

Корень x = −1 не принадлежит отрезку [0,5; 4], поэтому нас интересует только Кроме того, рассмотрим концы отрезка — Итого три числа: Поскольку требуется найти наименьшее значение функции, подставляем эти числа в исходную функцию:

y (0,5) = 2 · 0,5 2 − 4 ln 0,5 + 5 = 0,5 − 4 ln 0,5 + 5 = 5,5 − 4 ln 0,5;
y (1) = 2 · 1 2 − 4 ln 1 + 5 = 2 − 0 + 5 = 7;
y (4) = 2 · 4 2 − 4 ln 4 + 5 = 32 − 4 ln 4 + 5 = 37 − 4 ln 4.

В общем, выбирать особо не из чего. Ответ: 7. Потому что числа иррациональны, их нельзя записать в виде конечной десятичной дроби.

Задача. Найдите точку минимума функции:

y = 2 x − 5 ln ( x − 7) + 3

Снова считаем производную:

Под логарифмом стоит линейная функция Коэффициент при переменной x равен поэтому в числителе никаких дополнительных множителей не возникнет — только множитель 5, который стоит перед логарифмом.

Поскольку требуется найти точку минимума, считаем нули числителя и знаменателя:

2 x − 19 ⇒ x = 19 : 2 = 9,5;
x − 7 = 0 ⇒ x = 7.

Отмечаем эти точки на прямой, расставляем знаки производной между точками:

Итак, в точке x = 9,5 производная меняет знак с минуса на плюс, если считать слева — направо, в направлении стрелки. Это и есть точка минимума.

Задача. Найдите наибольшее значение функции на отрезке [−1,5; 1]:

y = 3 ln ( x + 2) − 3 x + 10

Находим нули числителя:

Нули знаменателя нас не интересуют, поскольку требуется найти значение функции. А когда знаменатель равен нулю, значение функции не определено.

Поскольку корень получаем три точки: Подставляем их в исходную функцию:

y (−1,5) = 3 ln (−1,5 + 2) − 3 · (−1,5) + 10 = 3 ln 0,5 + 14,5;
y (−1) = 3 ln (−1 + 2) − 3 · (−1) + 10 = 3 ln 1 + 13 = 0 + 13 = 13;
y (1) = 3 ln (1 + 2) − 3 · 1 + 10 = 3 ln 3 + 7.

Понятно, что числа нельзя записать в ответ. Остается только число 13 — это и будет наибольшее значение.

Содержание

Вынесение степени за знак логарифма
Нахождение точек максимума (мин) функции. Логарифмы
Логарифмические неравенства
🔥 Видео

Видео:Найдите наименьшее значение функции | Без Лайфхаков | ЕГЭ профильСкачать

Вынесение степени за знак логарифма

Еще одна полезная фишка, которая избавит вас от сложных производных:

ln ( f ( x )) k = k · ln f ( x )

Обратите внимание: в первом случае внутри логарифма стоит степень, для которой потребуется производная сложной функции. Во втором случае все намного проще, поскольку чаще всего это обычная линейная функция.

Этот прием часто встречается в задачах на вычисление максимального и минимального значения. В задачах на точки экстремума его почти не применяют. Прежде чем решать такую задачу, обязательно найдите ОДЗ логарифма. Если забыли, что это такое, см. «Что такое логарифм».

Задача. Найдите наименьшее значение функции на отрезке [−4; 1]:

y = 5 x − ln ( x + 5) 5

Итак, область допустимых значений логарифма — аргумент должен быть больше нуля. Имеем:

( x + 5) 5 > 0;
x + 5 > 0;
x > −5;
x ∈ (−5; +∞).

Теперь решаем задачу. Сначала немного преобразуем исходное выражение:

y = 5 x − 5 ln ( x + 5)

Это и есть вынесение степени за знак логарифма. Считаем производную:

Дальше все стандартно. Нас интересует значение функции, поэтому приравниваем числитель к нулю:

5 x + 20 = 0;
x = −4.

Полученное число x = −4 ∈ [−4; 1] совпадает с концом отрезка, поэтому кандидатов на наименьшее значение всего два: Оба числа подходят по ОДЗ. Поскольку требуется найти наименьшее значение, подставляем эти числа в исходную функцию:

y (−4) = 5 · (−4) − 5 · ln (−4 + 5) = −20 − 5 · ln 1 = −20;
y (1) = 5 · 1 − 5 · ln (1 + 5) = 5 − 5 ln 6.

Второе число — точно не ответ, поскольку его нельзя представить в виде десятичного числа. Значит, наименьшее значение функции равно −20.

Задача. Найдите точку максимума функции:

y = 18 ln x − x 2 + 5

ОДЗ логарифма: x > 0 ⇒ x ∈ (0; +∞). Считаем производную:

Поскольку требуется найти точку максимума, нас интересует и числитель, и знаменатель. Приравниваем их к нулю:

2 · (9 − x 2 ) = 0 ⇒ x 2 = 9 ⇒ x = ±3 — числитель;
x = 0 — знаменатель.

Получили три точки. Отмечаем эти точки и знаки производной на числовой прямой:

Требуется найти точку максимума — там, где плюс меняется на минус. Таких точек две: Но вспомним ОДЗ: Значит, точка не подходит. Остается точка это и будет ответ.

Видео:Наибольшее и наименьшее значение функции. 10 класс.Скачать

Нахождение точек максимума (мин) функции. Логарифмы

Здравствуйте, Дорогие друзья! Продолжаем рассматривать задания связанные с исследованием функций. Рекомендую повторить теорию , необходимую для решения задач на нахождение максимального (минимального) значения функции и на нахождение точек максимума (минимума) функции.

Задачи с логарифмами на нахождение наибольшего (наименьшего) значения функции мы уже рассмотрели . В этой статье рассмотрим три задачи, в которых стоит вопрос нахождения точек максимума (минимума) функций, при чём в заданной функции присутствует натуральный логарифм.

По определению логарифма – выражение стоящее под знаком логарифма должно быть больше нуля. *Это обязательно нужно учитывать не только в данных задачах, но и при решении уравнений и неравенств содержащих логарифм.

Алгоритм нахождения точек максимума (минимума) функции:

1. Вычисляем производную функции.

2. Приравниваем её к нулю, решаем уравнение.

3. Полученные корни отмечаем на числовой прямой. *Также на ней отмечаем точки, в которых производная не существует. Получим интервалы, на которых функция возрастает или убывает.

4. Определяем знаки производной на этих интервалах (подставляя произвольные значения из них в производную).

Найдите точку максимума функции у = ln (х–11)–5х+2

Сразу запишем, что х–11>0 (по определению логарифма), то есть х > 11.

Рассматривать функцию будем на интервале (11;∞).

Найдём производную заданной функции:

Найдем нули производной:

Точка х = 11 не входит в область определения функции и в ней производная не существует. Отмечаем на числовой оси две точки 11 и 11,2. Определим знаки производной функции, подставляя произвольные значения из интервалов (11;11,2) и (11,2;+∞) в найденную производную, и изобразим на рисунке поведение функции:

Таким образом, в точке х=11,2 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума.

Найдите точку максимума функции у=ln (х+5)–2х+9.

Найдите точку минимума функции у=4х– ln (х+5)+8

Сразу запишем, что х+5>0 (по свойству логарифма), то есть х>–5.

Рассматривать функцию будем на интервале (– 5;+∞).

Найдём производную заданной функции:

Найдем нули производной:

Точка х = –5 не входит в область определения функции и в ней производная не существует. Отмечаем на числовой оси две точки –5 и –4,75 . Определим знаки производной функции, подставляя произвольные значения из интервалов (–5;–4,75) и (–4,75;+∞) в найденную производную, и изобразим на рисунке поведение функции:

Таким образом, в точке х= –4,75 производная функции меняет знак с отрицательного на положительный, значит это искомая точка минимума.

Найдите точку минимума функции у=2х–ln (х+3)+7.

Найдите точку максимума функции у = х 2 –34х+140lnх–10

По свойству логарифма выражение, стоящее под его знаком больше нуля, то есть х > 0.

Функцию будем рассматривать на интервале (0; +∞).

Найдём производную заданной функции:

Найдем нули производной:

Решая квадратное уравнение, получим: D = 9 х₁ = 10 х₂ = 7.

Точка х = 0 не входит в область определения функции и в ней производная не существует. Отмечаем на числовой оси три точки 0, 7 и 10 .

Ось ох разбивается на интервалы: (0;7), (7;10), (10; +∞).

Определим знаки производной функции, подставляя произвольные значения из полученных интервалов в найденную производную, и изобразим на рисунке поведение функции:

Таким образом, в точке х = 7 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума.

Найдите точку максимума функции у = 2х 2 –13х+9lnх+8

В данной рубрике продолжим рассматривать задачи, не пропустите!

Видео:Математический анализ, 13 урок, Наибольшее и наименьшее значение функции на отрезкеСкачать

Логарифмические неравенства

Решая логарифмические неравенства, мы пользуемся свойством монотонности логарифмической функции. Также мы используем определение логарифма и основные логарифмические формулы.

Давайте повторим, что такое логарифмы:

Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить .

Основное логарифмическое тождество:

Основные формулы для логарифмов:

(Логарифм произведения равен сумме логарифмов)

(Логарифм частного равен разности логарифмов)

(Формула для логарифма степени)

Формула перехода к новому основанию:

Алгоритм решения логарифмических неравенств

Можно сказать, что логарифмические неравенства решаются по определенному алгоритму. Нам нужно записать область допустимых значений (ОДЗ) неравенства. Привести неравенство к виду Знак здесь может быть любой: Важно, чтобы слева и справа в неравенстве находились логарифмы по одному и тому же основанию.

И после этого «отбрасываем» логарифмы! При этом, если основание степени , знак неравенства остается тем же. Если основание такое, что знак неравенства меняется на противоположный.

Конечно, мы не просто «отбрасываем» логарифмы. Мы пользуемся свойством монотонности логарифмической функции. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает, и тогда большему значению х соответствует большее значение выражения .

Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. Большему значению аргумента х будет соответствовать меньшее значение

Важное замечание: лучше всего записывать решение в виде цепочки равносильных переходов.

Перейдем к практике. Как всегда, начнем с самых простых неравенств.

1. Рассмотрим неравенство log₃x > log₃5.
Поскольку логарифмы определены только для положительных чисел, необходимо, чтобы x был положительным. Условие x > 0 называется областью допустимых значений (ОДЗ) данного неравенства. Только при таких x неравенство имеет смысл.

Что делать дальше? Стандартный ответ, который дают школьники, — «Отбросить логарифмы!»

Что ж, эта формулировка лихо звучит и легко запоминается. Но почему мы все-таки можем это сделать?

Мы люди, мы обладаем интеллектом. Наш разум устроен так, что все логичное, понятное, имеющее внутреннюю структуру запоминается и применяется намного лучше, чем случайные и не связанные между собой факты. Вот почему важно не механически вызубрить правила, как дрессированная собачка-математик, а действовать осознанно.

Так почему же мы все-таки «отбрасываем логарифмы»?

Ответ простой: если основание больше единицы (как в нашем случае), логарифмическая функция монотонно возрастает, значит, большему значению x соответствует большее значение y и из неравенства log₃x₁ > log₃x₂ следует, что x₁ > x₂.

Обратите внимание, мы перешли к алгебраическому неравенству, и знак неравенства при этом — сохраняется.

Следующее логарифмическое неравенство тоже простое.

Начнём с области допустимых значений. Логарифмы определены только для положительных чисел, поэтому

Решая эту систему, получим: x > 0.

Теперь от логарифмического неравенства перейдем к алгебраическому — «отбросим» логарифмы. Поскольку основание логарифма больше единицы, знак неравенства при этом сохраняется.

А что же будет, если основание логарифма меньше единицы? Легко догадаться, что в этом случае при переходе к алгебраическому неравенству знак неравенства будет меняться.

Запишем ОДЗ. Выражения, от которых берутся логарифмы, должны быть положительно, то есть

Решая эту систему, получим: x > 4,5.

Поскольку , логарифмическая функция с основанием монотонно убывает. А это значит, что большему значению функции отвечает меньшее значение аргумента:

И если , то
2x − 9 ≤ x.

Получим, что x ≤ 9.

Учитывая, что x > 4,5, запишем ответ:

В следующей задаче показательное неравенство сводится к квадратному. Так что тему «квадратные неравенства» рекомендуем повторить.

Теперь более сложные неравенства:

4. Решите неравенство

5. Решите неравенство

Если , то . Нам повезло! Мы знаем, что основание логарифма больше единицы для всех значений х, входящих в ОДЗ.

Обратите внимание, что сначала мы полностью решаем неравенство относительно новой переменной t. И только после этого возвращаемся к переменной x. Запомните это и не ошибайтесь на экзамене!

Запомним правило: если в уравнении или неравенстве присутствуют корни, дроби или логарифмы — решение надо начинать с области допустимых значений. Поскольку основание логарифма должно быть положительно и не равно единице, получим систему условий:

Упростим эту систему:

Это область допустимых значений неравенства.

Мы видим, что переменная содержится в основании логарифма. Перейдем к постоянному основанию. Напомним, что

В данном случае удобно перейти к основанию 4.

Сделаем замену

Упростим неравенство и решим его методом интервалов:

Вернемся к переменной x:

Мы добавили условие x > 0 (из ОДЗ).

Ответ:

7. Следующая задача тоже решается с помощью метода интервалов

Как всегда, решение логарифмического неравенства начинаем с области допустимых значений. В данном случае

0″ src=»https://latex.codecogs.com/png.latex?%5Cfrac%3C2-3x%3E%3Cx%3E%3E0″ />Это условие обязательно должно выполняться, и к нему мы вернемся. Рассмотрим пока само неравенство. Запишем левую часть как логарифм по основанию 3:

Правую часть тоже можно записать как логарифм по основанию 3, а затем перейти к алгебраическому неравенству:

Видим, что условие 0″ src=»https://latex.codecogs.com/png.latex?%5Cfrac%3C2-3x%3E%3Cx%3E%3E0″ /> (то есть ОДЗ) теперь выполняется автоматически. Что ж, это упрощает решение неравенства.

Решаем неравенство методом интервалов:

Ответ:

Получилось? Что же, повышаем уровень сложности:

8. Решите неравенство:

Неравенство равносильно системе:

9. Решите неравенство:

Выражение 5 — x 2 навязчиво повторяется в условии задачи. А это значит, что можно сделать замену:

Поскольку показательная функция принимает только положительные значения, t > 0. Тогда

Неравенство примет вид:

Уже лучше. Найдем область допустимых значений неравенства. Мы уже сказали, что t > 0. Кроме того, ( t − 3) (5 9 · t − 1) > 0

Если это условие выполнено, то и частное будет положительным.

А еще выражение под логарифмом в правой части неравенства должно быть положительно, то есть (625 t − 2) 2 .

Это означает, что 625 t − 2 ≠ 0, то есть

Аккуратно запишем ОДЗ

и решим получившуюся систему, применяя метод интервалов.

Итак,

Ну что ж, полдела сделано — разобрались с ОДЗ. Решаем само неравенство. Сумму логарифмов в левой части представим как логарифм произведения:

«Отбросим» логарифмы. Знак неравенства сохраняется.

Перенесем все в левую часть и разложим по известной формуле разности квадратов:

0;» src=»https://latex.codecogs.com/png.latex?(t-3)%5E%3C2%3E-(625t-2)%5E%3C2%3E%3E0;» />
0;» src=»https://latex.codecogs.com/png.latex?(t-3-625t+2)(t-3+625t-2)%3E0;» />
0.» src=»https://latex.codecogs.com/png.latex?(-624t-1)(626t-5)%3E0.» />
Вспомним, что (это ОДЗ неравенства) и найдем пересечение полученных промежутков.

Получим, что

Вернемся к переменной x

Поскольку

9;» src=»https://latex.codecogs.com/gif.latex?x%5E%3C2%3E%3E&space;9;» /> 0″ src=»https://latex.codecogs.com/png.latex?(x-3)(x+3)%3E0″ />Ответ:

10. Еще один прием, упрощающий решение логарифмических неравенств, — переход к постоянному основанию. Покажем, как использовать переход к другому основанию и обобщенный метод интервалов.

Воспользуемся формулой и перейдем к основанию 10:

Применим обобщенный метод интервалов. Выражение в левой части неравенства можно записать как функцию

Эта функция может менять знак в точках, где она равна нулю или не существует.

Выражение lg | x − 3| равно нулю, если | x − 3| = 1, то есть x = 4 или x = 2.

Выражение lg (| x| − 2) равно нулю, если | x| = 3, то есть в точках 3 и −3.

Отметим эти точки на числовой прямой, с учетом ОДЗ неравенства.

Найдем знак функции g(x) на каждом из промежутков, на которые эти точки разбивают область допустимых значений. Точно так же мы решали методом интервалов обычные рациональные неравенства.

Ответ:

11. А в следующей задаче спрятаны целых две ловушки для невнимательных абитуриентов.

Запишем ОДЗ:

0\ x+2neq 1\ 36+16x-x^>0\ xneq 18 endright. : : : : : : : : Leftrightarrow : : : : : left <beginx>-2\ xneq -1\ xin (-2;18) endright.» src=»https://latex.codecogs.com/png.latex?%5Cleft%5C%3C%5Cbegin%3Cmatrix%3E&space;x+2%3E0%5C%5C&space;x+2%5Cneq&space;1%5C%5C&space;36+16x-x%5E%3C2%3E%3E0%5C%5C&space;x%5Cneq&space;18&space;%5Cend%3Cmatrix%3E%5Cright.&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5CLeftrightarrow&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5Cleft%5C%3C%5Cbegin%3Cmatrix%3E&space;x%3E-2%5C%5C&space;x%5Cneq&space;-1%5C%5C&space;x%5Cin&space;(-2;18)&space;%5Cend%3Cmatrix%3E%5Cright.» />
Итак, Это ОДЗ.

Обратите внимание, что .

Это пригодится вам при решении неравенства.

Упростим исходное неравенство:

Теперь главное – не спешить. Мы уже говорили, что задача непростая – в ней расставлены ловушки. В первую вы попадете, если напишете, что Ведь выражение в данном случае не имеет смысла, поскольку x x — 18) 2 =(18 — x) 2 . Тогда:

Вторая ловушка – попроще. Запись означает, что сначала надо вычислить логарифм, а потом возвести полученное выражение в квадрат. Поэтому:

Дальше – всё просто. Сделаем замену

Выражение в левой части этого неравенства не может быть отрицательным, поэтому t = 2. Тогда

— не удовлетворяет ОДЗ;

Мы рассмотрели основные приемы решения логарифмических неравенств — от простейших до сложных, которые решаются с помощью обобщенного метода интервалов. Однако есть еще один интересный метод, помогающий справиться и показательными, и с логарифмическими, и с многими другими видами неравенств. Это метод рационализации (замены множителя). О нем — в следующей статье.