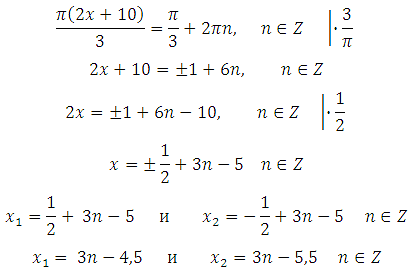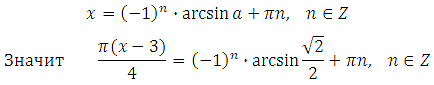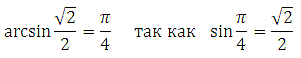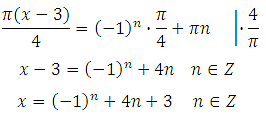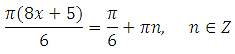Найдите наибольший отрицательный корень уравнения:
Решением уравнения cosx=a являются два корня:
Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.
Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.
Общая рекомендация для всех подобных задач: для начала берите диапазон n от –2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: –3 и 3, –4 и 4 и так далее. Вычисляем:
При n = – 2 х1= 3 (– 2) – 4,5 = – 10,5 х2= 3 (– 2) – 5,5 = – 11,5
При n = – 1 х1= 3 (– 1) – 4,5 = – 7,5 х2= 3 (– 1) – 5,5 = – 8,5
При n = 0 х1= 3∙0 – 4,5 = – 4,5 х2= 3∙0 – 5,5 = – 5,5
При n = 1 х1= 3∙1 – 4,5 = – 1,5 х2= 3∙1 – 5,5 = – 2,5
При n = 2 х1= 3∙2 – 4,5 = 1,5 х2= 3∙2 – 5,5 = 0,5
Получили, что наибольший отрицательный корень равен –1,5
Найдите наименьший положительный корень уравнения:
Решением уравнения sin x = a являются два корня:
Либо (он объединяет оба указанные выше):
Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от –90 о до 90 о синус которого равен a.
Значит
Выразим x (умножим на 4 и разделим на Пи):
Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n получим отрицательные корни. Поэтому будем подставлять n=0,1,2 …
При n = 0 х = (– 1) 0 + 4∙0 + 3 = 4
При n = 1 х = (– 1) 1 + 4∙1 + 3 = 6
При n = 2 х = (– 1) 2 + 4∙2 + 3 = 12
Проверим при n=–1 х=(–1) –1 + 4∙(–1) + 3 = –2
Значит наименьший положительный корень равен 4.
Найдите наименьший положительный корень уравнения:
Решением уравнения tg x = a является корень:
Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90 о до 90 о , тангенс которого равен a.
Значит
Выразим x (умножим на 6 и разделим на Пи):
Найдём наименьший положительный корень. Подставим значения n=0,1,2,3 … Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:
Таким образом, наименьший положительный корень равен 0,25.
Видео:Решите уравнение: tg пx/4 = -1 В ответе напишите наибольший отрицательный корень.Скачать
Тригонометрические уравнения
Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно. Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.
В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.
Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.
Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.
Понимание раздела «Тригонометрия» в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.
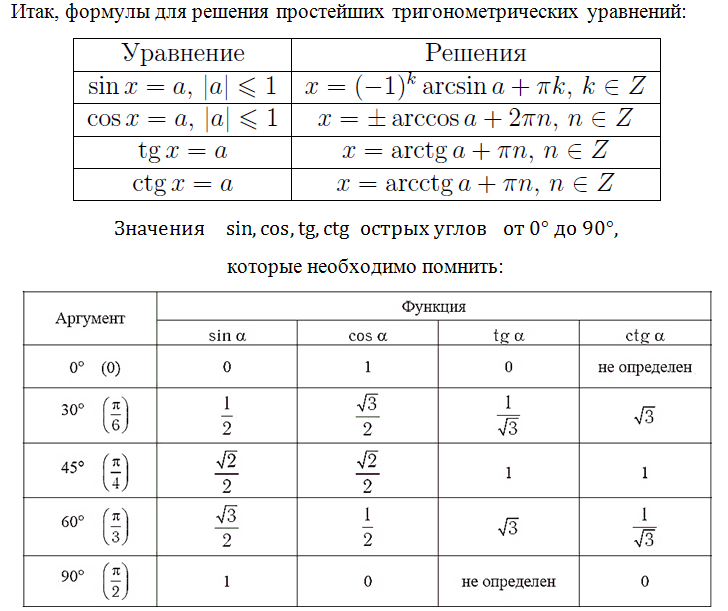
В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:
Знание этих значений необходимо, это «азбука», без которой невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да просто вы именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.
Алгоритм восстановления этих значений прост, он также приведён в теории, полученной вами во втором письме после подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».
Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с использованием угла х для соответствующих уравнений: cosx=a, sinx=a, tgx=a, где х может быть и выражением. В примерах ниже у нас аргумент задан именно выражением.
Итак, рассмотрим следующие задачи:
Найдите корень уравнения:
В ответе запишите наибольший отрицательный корень.
Решением уравнения cos x = a являются два корня:
Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.
Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.
Общая рекомендация для всех подобных задач: для начала берите диапазон n от – 2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: – 3 и 3, – 4 и 4 и так далее.
При n = – 2 х1= 3 (– 2) – 4,5 = – 10,5 х2= 3 (– 2) – 5,5 = – 11,5
При n = – 1 х1= 3 (– 1) – 4,5 = – 7,5 х2= 3 (– 1) – 5,5 = – 8,5
При n = 0 х1= 3∙0 – 4,5 = – 4,5 х2= 3∙0 – 5,5 = – 5,5
При n = 1 х1= 3∙1 – 4,5 = – 1,5 х2= 3∙1 – 5,5 = – 2,5
При n = 2 х1= 3∙2 – 4,5 = 1,5 х2= 3∙2 – 5,5 = 0,5
Получили, что наибольший отрицательный корень равен –1,5
В ответе напишите наименьший положительный корень.
Решением уравнения sin x = a являются два корня:
Либо (он объединяет оба указанные выше):
Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от – 90 о до 90 о синус которого равен a.
Выразим x (умножим обе части уравнения на 4 и разделим на Пи):
Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n = 0,1,2 …
При n = 0 х = (– 1) 0 + 4∙0 + 3 = 4
При n = 1 х = (– 1) 1 + 4∙1 + 3 = 6
При n = 2 х = (– 1) 2 + 4∙2 + 3 = 12
Проверим при n = –1 х = (–1) –1 + 4∙(–1) + 3 = –2
Значит наименьший положительный корень равен 4.
В ответе напишите наименьший положительный корень.
Решением уравнения tg x = a является корень:
Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90 о до 90 о , тангенс которого равен a.
Выразим x (умножим обе части уравнения на 6 и разделим на Пи):
Найдём наименьший положительный корень. Подставим значения n = 1,2,3. Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:
Таким образом, наименьший положительный корень равен 0,25.
Определение котангенса: Арккотангенсом числа a (a – любое число) называется угол x принадлежащий интервалу (0;П), котангенс которого равен a.
Здесь хочу добавить, что в уравнениях в правой части может стоять отрицательное число, то есть тригонометрическая функция от аргумента может иметь отрицательное значение. Если в ходе решения вы не сможете определить угол, например, для
то данные формулы вам помогут:
Спасибо за внимание, учитесь с удовольствием!
Видео:Найдите корни уравнения: cosπ(x−7)/3=1/2 В ответ запишите наибольший отрицательный корень.Скачать
Простейшие тригонометрические уравнения. Часть 1
Простейшими называются тригонометрические уравнения следующих четырёх видов:
Любое тригонометрическое уравнение в конечном счёте сводится к решению одного или нескольких простейших. К сожалению, на этом заключительном стандартном шаге школьники часто допускают ошибки, что ведет к потере баллов на ЕГЭ. Именно поэтому так важна данная тема.
Существуют два подхода к решению простейших тригонометрических уравнений.
Первый подход — бессмысленный и тяжёлый. Следуя ему, надо выучить по шпаргалке общие формулы, а также все частные случаи. Польза от этого столь же невелика, как от зубрежки шестнадцати строк заклинаний на непонятном языке. Мы отказываемся от такого подхода раз и навсегда.
Второй подход — логический и наглядный. Для решения простейших тригонометрических уравнений мы пользуемся тригонометрическим кругом и определениями тригонометрических функций.
Видео:sinπx/3=0,5 В ответе напишите наименьший положительный корень/ наибольший отрицательный кореньСкачать
Уравнения и
Напомним, что — абсцисса точки на единичной окружности, соответствующей углу , а — её ордината.
Из определения синуса и косинуса следует, что уравнения и имеют решения только при условии .
Абитуриент, будь внимателен! Уравнения или решений не имеют!
Начнём с самых простых уравнений.
. .
Мы видим, что на единичной окружности имеется лишь одна точка с абсциссой 1:
Эта точка соответствует бесконечному множеству углов: . Все они получаются из нулевого угла прибавлением целого числа полных углов (т. е. нескольких полных оборотов как в одну, так и в другую сторону).
Следовательно, все эти углы могут быть записаны одной формулой:
Это и есть множество решений данного уравнения. Напоминаем, что — это множество целых чисел.
Снова видим, что на единичной окружности есть лишь одна точка с абсциссой :
Эта точка соответствует углу и всем углам, отличающихся от на несколько полных оборотов в обе стороны, т. е. на целое число полных углов. Следовательно, все решения данного уравнения записываются формулой:
. .
Отмечаем на тригонометрическом круге единственную точку с ординатой :
И записываем ответ:
Обсуждать тут уже нечего, не так ли? 🙂
Можете, кстати, записать ответ и в другом виде:
Это — дело исключительно вашего вкуса.
Заодно сделаем первое полезное наблюдение. Чтобы описать множество углов, отвечающих одной-единственной точке тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить .
На тригонометрическом круге имеются две точки с ординатой 0:
Эти точки соответствуют углам Все эти углы получаются из нулевого угла прибавлением целого числа углов (т. е. с помощью нескольких полуоборотов в обе стороны). Таким образом,
Точки, лежащие на концах диаметра тригонометрического круга, мы будем называть диаметральной парой.
Точки с абсциссой 0 также образуют диаметральную пару, на сей раз вертикальную:
Все углы, отвечающие этим точкам, получаются из — прибавлением целого числа углов (полуоборотов):
Теперь мы можем сделать и второе полезное наблюдение.
Чтобы описать множество углов, отвечающих диаметральной паре точек тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить .
Переходим к следующему этапу. Теперь в правой части будет стоять табличное значение синуса или косинуса (отличное от 0 или ). Начинаем с косинуса.
Имеем вертикальную пару точек с абсциссой :
Все углы, соответствующие верхней точке, описываются формулой (вспомните первое полезное наблюдение!):
Аналогично, все углы, соответствующие нижней точке, описываются формулой:
Обе серии решений можно описать одной формулой:
Остальные уравнения с косинусом решаются совершенно аналогично. Мы приводим лишь рисунок и ответ.
Теперь рассмотрим уравнения с синусом. Тут ситуация немного сложнее.
Имеем горизонтальную пару точек с ординатой :
Углы, отвечающие правой точке:
Углы, отвечающие левой точке:
Описывать эти две серии одной формулой никто не заставляет. Можно записать ответ в таком виде:
Тем не менее, объединяющая формула существует, и её надо знать. Выглядит она так:
На первый взгляд совершенно не ясно, каким образом она дает обе серии решений. Но давайте посмотрим, что получается при чётных . Если , то
Мы получили первую серию решений . А если — нечетно, , то
Это вторая серия .
Обратим внимание, что в качестве множителя при обычно ставится правая точка, в данном случае .
Остальные уравнения с синусом решаются точно так же. Мы приводим рисунок, запись ответа в виде совокупности двух серий и объединяющую формулу.
На этом с синусом и косинусом пока всё. Переходим к тангенсу.
Видео:Решите уравнение sin п(4x-3)/4 = 1. В ответе напишите наибольший отрицательный корень.Скачать
Линия тангенсов.
Начнём с геометрической интерпретации тангенса — так называемой линии тангенсов. Это касательная к единичной окружности, параллельная оси ординат (см. рисунок).
Из подобия треугольников и имеем:
Мы рассмотрели случай, когда находится в первой четверти. Аналогично рассматриваются случаи, когда находится в остальных четвертях. В результате мы приходим к следующей геометрической интерпретации тангенса.
Тангенс угла равен ординате точки , которая является точкой пересечения линии тангенсов и прямой , соединяющей точку с началом координат.
Вот рисунок в случае, когда находится во второй четверти. Тангенс угла отрицателен.
Видео:tg (π(8x+9))/3=-√3 в ответе напишите наибольший отрицательный кореньСкачать
Уравнение
Заметим, что тангенс может принимать любые действительные значения. Иными словами, уравнение имеет решения при любом .
.
Имеем диаметральную горизонтальную пару точек:
Эта пара, как мы уже знаем, описывается формулой:
Имеем диаметральную пару:
Вспоминаем второе полезное наблюдение и пишем ответ:
Остальные уравнения с тангенсом решаются аналогично. Мы приводим лишь рисунки и ответы.
На этом заканчиваем пока и с тангенсом.
Уравнение нет смысла рассматривать особо. Дело в том, что:
уравнение равносильно уравнению ;
при уравнение равносильно уравнению .
Впрочем, существует также и линия котангенсов, но. . . Об этом мы вам расскажем на занятиях 🙂
Итак, мы разобрали простейшие тригонометрические уравнения, содержащие в правой части табличные значения тригонометрических функций. Именно такие задачи встречаются в части В вариантов ЕГЭ.
А что делать, например, с уравнением ? Для этого надо сначала познакомиться с обратными тригонометрическими функциями. О них мы расскажем вам в следующей статье.
📸 Видео
Решите уравнение tg п(x+2)/3 = - корень из 3. В ответе напишите наибольший отрицательный корень.Скачать
Решите уравнение tg п(x-3)/6 = 1/корень из 3. В ответе напишите наибольший отрицательный корень.Скачать
tg pi(2x+5)/6=корень из 3. В ответе запишите наибольший отрицательный корень (проф. ЕГЭ, задача 6)Скачать
Найдите наименьший положительный корень уравнения sin pi x/3=-(корень из 3)/2 (проф. ЕГЭ задача №6)Скачать
3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать
Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать
Отбор корней по окружностиСкачать
Найдите наибольший отрицательный корень 251Скачать
Как найти наибольший корень уравнения #shorts | ЕГЭ 2022 по математике | Эйджей из ВебиумаСкачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
ЕГЭ-ПРОФИЛЬ. ЗАДАНИЕ-1. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯСкачать
Решите уравнение sin(πx/3) = 1/2 В ответе напишите наименьший положительный корень.Скачать
Находим решение тригонометрического уравнения на интервале Алгебра 10 классСкачать
Как решать уравнения с косинусом ? / ЕГЭ ПРОФИЛЬ # 26669Скачать
