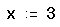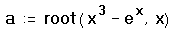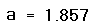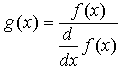Как найти начальное приближение корня уравнения

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Как найти начальное приближение корня уравнения

Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.

Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.

Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.

Рассмотрим пример, как найти a — решение уравнения e x = x 3 . Для этого выполните следующие шаги:

• Определите начальное значение переменной x. Введите x:3. Выбор начального приближения влияет на корень, возвращаемый Mathcad (если выражение имеет несколько корней).

• Определите выражение, которое должно быть обращено в ноль. Для этого перепишите уравнение e x = x 3 в виде x 3 — e x = 0. Левая часть этого выражения и является вторым аргументом функции root
• Определите переменную a как корень уравнения. Для этого введите a:root(x^3[Space]-e^x[Space],x).

• Напечатайте a=, чтобы увидеть значение корня.

При использовании функции root имейте в виду следующее:

• Удостоверьтесь, что переменной присвоено начальное значение до начала использования функции root.
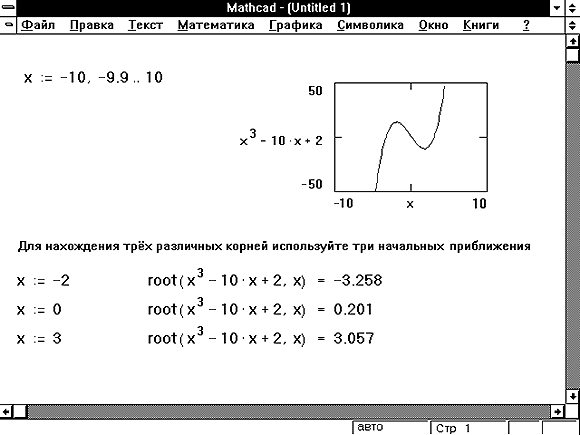
• Для выражения с несколькими корнями, например x 2 — 1 = 0, начальное значение определяет корень, который будет найден Mathcad. На Рисунке 1 приведен пример, в котором функция root возвращает различные значения, каждое из которых зависит от начального приближения.
• Mathcad позволяет находить как комплексные, так и вещественные корни. Для поиска комплексного корня следует взять в качестве начального приближения комплексное число.
• Задача решения уравнения вида f(x) = g(x) эквивалентна задаче поиска корня выражения f(x) — g(x) =0. Для этого функция root может быть использована следующим образом:

Функция root предназначена для решения одного уравнения с одним неизвестным. Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.

Рисунок 1: Использование графика и функции root для поиска корней уравнения.

Что делать, когда функция root не сходится

Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.

Если после многих итераций Mathcad не может найти подходящего приближения, то появляется сообщение об ошибке “отсутствует сходимость”. Эта ошибка может быть вызвана следующими причинами:

• Уравнение не имеет корней.
• Корни уравнения расположены далеко от начального приближения.
• Выражение имеет локальные максимумы или минимумы между начальным приближением и корнями.
• Выражение имеет разрывы между начальным приближением и корнями.
• Выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).

Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find

Некоторые советы по использованию функции root

В этом разделе приведены несколько советов по использованию функции root:

• Для изменения точности, с которой функция root ищет корень, можно изменить значение встроенной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите из меню Математика команду Встроенные переменные и введите подходящее значение в поле TOL. Нажав “OK”, выберите из меню Математика команду Пересчитать всё, чтобы обновить все вычисления в рабочем документе с использованием нового значения переменной TOL.
• Если уравнение имеет несколько корней, пробуйте использовать различные начальные приближения, чтобы найти их. Использование графика функции полезно для нахождения числа корней выражения, их расположения и определения подходящих начальных приближений. Рисунок 1 показывает пример. Если два корня расположены близко друг от друга, можно уменьшить TOL, чтобы различить их.
• Если f(x) имеет малый наклон около искомого корня, функция может сходиться к значению r, отстоящему от корня достаточно далеко . В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x)=0 на g(x)=0, где

Решение уравнений с параметром

Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции

Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.

Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.

Рисунок 2: Определение функции пользователя с функцией root.

Нахождение корней полинома

Для нахождения корней выражения, имеющего вид

лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.

Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.

Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.

Рисунок 4: Использование функции polyroots для поиска корней полинома.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Как найти начальное приближение корня уравнения

Глава 4. Решение уравнений

4.1 Функция root

Функция root используется для решения одного уравнения с одним неизвестным. Перед началом решения желательно построить график функции, чтобы проверить, есть ли корни, то есть пересекает ли график ось абсцисс. Начальное приближение лучше всего выбрать по графику поближе к корню, так как итерационные методы весьма чувствительны к выбору начального приближения.

Обращение к функции осуществляется следующим образом:

root ( f ( x ), x ), где f ( x ) – выражение, равное нулю; x – аргумент, варьируя который, система ищет значение, обращающее в нуль ( рис. 4.1 ).

Уравнение

начальное приближение

решение

или

другие корни

Задан интервал поиска корней

Рис. 4. 1 Использование функции root

Функция f ( x ) и аргумент x должны быть скалярами, то есть результат вычисления функции – число, а не вектор или матрица. Функция root использует метод секущих. Корень уравнения – ближайшее к начальному приближению значение x , обращающее функцию f ( x ) в нуль. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.

Mathcad позволяет вместо начального приближения задавать диапазон значений аргумента, в котором лежит значение искомого корня. В этом случае обращение к функции root должно иметь четыре параметра:

root ( f ( x ), x , а, b ),

где a и b – границы интервала, в котором лежит один корень уравнения. Внутри интервала не должно быть больше одного корня, так как Mathcad выводит на экран лишь один корень, лежащий внутри интервала.

Значение функции на границах интервала должно быть разного знака, иначе, возможно, корень не будет найден.

Если уравнение не имеет действительных корней, то есть на графике функция f ( x ) нигде не равна нулю, то для вывода комплексных корней надо ввести начальное приближение в комплексной форме (рис. 4.2) .

Если функция имеет мнимый корень,

то начальное приближение задается комплексным числом

— начальное приближение

Рис. 4. 2 Решение уравнения с комплексными корнями

Для ввода мнимой единицы надо ввести с клавиатуры 1 i или 1 j .

Если уравнение имеет несколько корней, то для их нахождения можно использовать разложение функции f ( x ) на простые множители:

где x _1, x ₂ , , x_n – корни уравнения. Начальное приближение можно задать только для первого корня. В качестве функции f ( x ) нужно взять

,

где ,

и т. д. (рис. 4.3)

у этой функции 3 корня

диапазон значений х для вывода графика

Рис. 4. 3 Определение трех корней уравнения

Если функция f ( x ) имеет малый наклон вблизи искомого корня, то функция root ( f ( x ), x ) может сходиться к значению, довольно далеко отстоящему от корня. В таком случае для уточнения корня необходимо уменьшить значение погрешности вычислений, задаваемое встроенной переменной TOL . Для этого:

1) в стандартном меню Mathcad выберите команду Tools → Worksheet Options → Built – In Variables (Инструменты → Параметры документов → Встроенные переменные);

2) в открывшемся окне поменяйте значение Convergence Tolerance ( TOL ) (Погрешность сходимости).

Чем меньше константа TOL , тем ближе к нулю будет значение функции при найденном корне уравнения, но тем больше будет время вычисления корня.

Для повышения точности расчета корня можно заменить f ( x ) на

.

Корень можно найти и по графику, увеличив масштаб. Для этого необходимо:

1) выделить график, щелкнув левой кнопкой мыши внутри графика;

2)в главном меню Mathcad выбрать команду Format → Graph → Zoom (Формат→График→Масштаб);

3) при нажатии левой кнопки мыши обвести пунктирной линией область графика вблизи искомого корня, которую надо увеличить;

4) в открытом окне X – Y Zoom (Масштаб по осям X – Y ) нажать кнопку Zoom .

Прямо с графика можно передать в буфер обмена численное значение корня. Для этого выполните следующие действия:

1) Выделите график, щелкнув левой кнопкой мыши внутри графика,

2) в главном меню Mathcad выберите команду Format → Graph → Trace (Формат→График→Трассировка),

3) щелкните левой кнопкой мыши внутри графика – появится перекрестье осей,

4) двигая мышь при нажатой левой кнопке, установите перекрестье на пересечении графика с осью абсцисс. При этом численные значения координат перекрестья появляются в открытом окне X – Y Trace (Трассировка X и Y ).

5) правильно выбрав положение перекрестья, нажмите кнопки Copy X и Copy Y – численные значения будут помещены в буфер

6) вне поля графика запишите имя, которое хотите дать корню, и оператор присваивания :=. Нажмите кнопку Paste (Вставить) в стандартном меню Mathcad или в контекстном меню, открывающемся при нажатии правой кнопки мыши.

Рис. 4. 4 Определение корня уравнения по графику

В окне X – Y Trace есть пункт Track Data Points (Отмечать расчетные точки). Если установить этот флажок, при перемещении мыши пунктирное перекрестье на графике будет перемещаться скачками, отмечая расчетные значения функции. Если флажок снять, движение перекрестья становится плавным.

При работе с Mathcad постоянно пользуйтесь правой кнопкой мыши (в контекстном меню каждый раз появляются новые, наиболее нужные в данный момент функции). Щелкните правой кнопкой мыши на графике: в открывшемся контекстном меню есть пункты Zoom и Trace .

Видео:Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать

Численные методы: решение нелинейных уравнений

Задачи решения уравнений постоянно возникают на практике, например, в экономике, развивая бизнес, вы хотите узнать, когда прибыль достигнет определенного значения, в медицине при исследовании действия лекарственных препаратов, важно знать, когда концентрация вещества достигнет заданного уровня и т.д.

В задачах оптимизации часто необходимо определять точки, в которых производная функции обращается в 0, что является необходимым условием локального экстремума.

В статистике при построении оценок методом наименьших квадратов или методом максимального правдоподобия также приходится решать нелинейные уравнения и системы уравнений.

Итак, возникает целый класс задач, связанных с нахождением решений нелинейных уравнений, например, уравнения или уравнения и т.д.

В простейшем случае у нас имеется функция , заданная на отрезке ( a , b ) и принимающая определенные значения.

Каждому значению x из этого отрезка мы можем сопоставить число , это и есть функциональная зависимость, ключевое понятие математики.

Нам нужно найти такое значение при котором такие называются корнями функции

Визуально нам нужно определить точку пересечения графика функции с осью абсцисс.

Видео:🔴 Найдите корень уравнения 2+9x=4x+3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

Метод деления пополам

Простейшим методом нахождения корней уравнения является метод деления пополам или дихотомия.

Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом.

Алгоритм состоит в следующем.

Предположим, мы нашли две точки и , такие что и имеют разные знаки, тогда между этими точками находится хотя бы один корень функции .

Поделим отрезок пополам и введем среднюю точку .

Тогда либо , либо .

Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее, достижения требуемой точности.

Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его.

Заметьте, описанный алгоритм применим для любой непрерывной функции.

К достоинствам метода деления пополам следует отнести его высокую надежность и простоту.

Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.

Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое, чем больше сделано итераций, тем точнее определен корень.

Видео:Найти корень уравнения на заданном интервале (MathCad)Скачать

Метод Ньютона: теоретические основы

Классический метод Ньютона или касательных заключается в том, что если — некоторое приближение к корню уравнения , то следующее приближение определяется как корень касательной к функции , проведенной в точке .

Уравнение касательной к функции в точке имеет вид:

В уравнении касательной положим и .

Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем:

Сходимость метода касательных квадратичная, порядок сходимости равен 2.

Таким образом, сходимость метода касательных Ньютона очень быстрая.

Запомните этот замечательный факт!

Без всяких изменений метод обобщается на комплексный случай.

Если корень является корнем второй кратности и выше, то порядок сходимости падает и становится линейным.

Упражнение 1. Найти с помощью метода касательных решение уравнения на отрезке (0, 2).

Упражнение 2. Найти с помощью метода касательных решение уравнения на отрезке (1, 3).

К недостаткам метода Ньютона следует отнести его локальность, поскольку он гарантированно сходится при произвольном стартовом приближении только, если везде выполнено условие , в противной ситуации сходимость есть лишь в некоторой окрестности корня.

Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге.

Видео:АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать

Визуализация метода Ньютона

Метод Ньютона (метод касательных) применяется в том случае, если уравнение f(x) = 0 имеет корень , и выполняются условия:

1) функция y= f(x) определена и непрерывна при ;

2) f(a)·f(b) 0. Таким образом, выбирается точка с абсциссой x₀, в которой касательная к кривой y=f(x) на отрезке [a;b] пересекает ось Ox. За точку x₀ сначала удобно выбирать один из концов отрезка.

Рассмотрим метод Ньютона на конкретном примере.

Пусть нам дана возрастающая функция y = f(x) =x 2 -2, непрерывная на отрезке (0;2), и имеющая f ‘(x) = 2x > 0 и f »(x) = 2 > 0.

Уравнение касательной в общем виде имеет представление:

В нашем случае: y-y₀=2x₀·(x-x₀). В качестве точки x₀ выбираем точку B₁(b; f(b)) = (2,2). Проводим касательную к функции y = f(x) в точке B₁, и обозначаем точку пересечения касательной и оси Ox точкой x₁. Получаем уравнение первой касательной:y-2=2·2(x-2), y=4x-6.

Точка пересечения касательной и оси Ox: x₁ =

Рисунок 2. Результат первой итерации

Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x₁, получаем точку В₂ =(1.5; 0.25). Снова проводим касательную к функции y = f(x) в точке В₂, и обозначаем точку пересечения касательной и оси Ox точкой x₂.

Точка пересечения касательной и оси Ox: x₂ = .

Рисунок 3. Вторая итерация метода Ньютона

Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x₂, получаем точку В₃ и так далее.

В3 = ()

Рисунок 4. Третий шаг метода касательных

Первое приближение корня определяется по формуле:

= 1.5.

Второе приближение корня определяется по формуле:

=

Третье приближение корня определяется по формуле:

Таким образом, i-ое приближение корня определяется по формуле:

Вычисления ведутся до тех пор, пока не будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или заданной точности e — до выполнения неравенства |xi—xi-1|

using namespace std;

float f(double x) //возвращает значение функции f(x) = x^2-2

float df(float x) //возвращает значение производной

float d2f(float x) // значение второй производной

int _tmain(int argc, _TCHAR* argv[])

int exit = 0, i=0;//переменные для выхода и цикла

double x0,xn;// вычисляемые приближения для корня

double a, b, eps;// границы отрезка и необходимая точность

cin>>a>>b; // вводим границы отрезка, на котором будем искать корень

cin>>eps; // вводим нужную точность вычислений

if (a > b) // если пользователь перепутал границы отрезка, меняем их местами

if (f(a)*f(b)>0) // если знаки функции на краях отрезка одинаковые, то здесь нет корня

cout 0) x0 = a; // для выбора начальной точки проверяем f(x0)*d2f(x0)>0 ?

xn = x0-f(x0)/df(x0); // считаем первое приближение

cout eps) // пока не достигнем необходимой точности, будет продолжать вычислять

xn = x0-f(x0)/df(x0); // непосредственно формула Ньютона

> while (exit!=1); // пока пользователь не ввел exit = 1

Посмотрим, как это работает. Нажмем на зеленый треугольник в верхнем левом углу экрана, или же клавишу F5.

Если происходит ошибка компиляции «Ошибка error LNK1123: сбой при преобразовании в COFF: файл недопустим или поврежден», то это лечится либо установкой первого Service pack 1, либо в настройках проекта Свойства -> Компоновщик отключаем инкрементную компоновку.

Рис. 4. Решение ошибки компиляции проекта

Мы будем искать корни у функции f(x) = x2-2.

Сначала проверим работу приложения на «неправильных» входных данных. На отрезке [3; 5] нет корней, наша программа должна выдать сообщение об ошибке.

У нас появилось окно приложения:

Рис. 5. Ввод входных данных

Введем границы отрезка 3 и 5, и точность 0.05. Программа, как и надо, выдала сообщение об ошибке, что на данном отрезке корней нет.

Рис. 6. Ошибка «На этом отрезке корней нет!»

Выходить мы пока не собираемся, так что на сообщение «Exit?» вводим «0».

Теперь проверим работу приложения на корректных входных данных. Введем отрезок [0; 2] и точность 0.0001.

Рис. 7. Вычисление корня с необходимой точностью

Как мы видим, необходимая точность была достигнута уже на 4-ой итерации.

Чтобы выйти из приложения, введем «Exit?» => 1.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Метод секущих

Чтобы избежать вычисления производной, метод Ньютона можно упростить, заменив производную на приближенное значение, вычисленное по двум предыдущим точкам:

/

Итерационный процесс имеет вид:

где .

Это двухшаговый итерационный процесс, поскольку использует для нахождения последующего приближения два предыдущих.

Порядок сходимости метода секущих ниже, чем у метода касательных и равен в случае однократного корня .

Эта замечательная величина называется золотым сечением:

Убедимся в этом, считая для удобства, что .

Таким образом, с точностью до бесконечно малых более высокого порядка

Отбрасывая остаточный член, получаем рекуррентное соотношение, решение которого естественно искать в виде .

После подстановки имеем: и

Для сходимости необходимо, чтобы было положительным, поэтому .

Поскольку знание производной не требуется, то при том же объёме вычислений в методе секущих (несмотря на меньший порядок сходимости) можно добиться большей точности, чем в методе касательных.

Отметим, что вблизи корня приходится делить на малое число, и это приводит к потере точности (особенно в случае кратных корней), поэтому, выбрав относительно малое , выполняют вычисления до выполнения и продолжают их пока модуль разности соседних приближений убывает.

Как только начнется рост, вычисления прекращают и последнюю итерацию не используют.

Такая процедура определения момента окончания итераций называется приемом Гарвика.

Видео:Математика 5 класс. Уравнение. Корень уравненияСкачать

Метод парабол

Рассмотрим трехшаговый метод, в котором приближение определяется по трем предыдущим точкам , и .

Для этого заменим, аналогично методу секущих, функцию интерполяционной параболой проходящей через точки , и .

В форме Ньютона она имеет вид:

Точка определяется как тот из корней этого полинома, который ближе по модулю к точке .

Порядок сходимости метода парабол выше, чем у метода секущих, но ниже, чем у метода Ньютона.

Важным отличием от ранее рассмотренных методов, является то обстоятельство, что даже если вещественна при вещественных и стартовые приближения выбраны вещественными, метод парабол может привести к комплексному корню исходной задачи.

Этот метод очень удобен для поиска корней многочленов высокой степени.

Видео:Числовое решение. Функция root в MathCAD 14 (28/34)Скачать

Метод простых итераций

Задачу нахождения решений уравнений можно формулировать как задачу нахождения корней: , или как задачу нахождения неподвижной точки.

Пусть и — сжатие: (в частности, тот факт, что — сжатие, как легко видеть, означает, что).

По теореме Банаха существует и единственна неподвижная точка

Она может быть найдена как предел простой итерационной процедуры

где начальное приближение — произвольная точка промежутка .

Если функция дифференцируема, то удобным критерием сжатия является число . Действительно, по теореме Лагранжа

Таким образом, если производная меньше единицы, то является сжатием.

Условие существенно, ибо если, например, на [0,1] , то неподвижная точка отсутствует, хотя производная равна нулю. Скорость сходимости зависит от величины . Чем меньше , тем быстрее сходимость.

Рассмотрим уравнение: .

Если в качестве взять функцию , то соответствующая итерационная процедура будет иметь вид: . Как нетрудно убедиться, метод итераций в данном случае расходится при любой начальной точке , не совпадающей с собственно неподвижной точкой .

Однако можно в качестве можно взять, например, функцию . Соответствующая итерационная процедура имеет вид: .

Эти итерации сходятся к неподвижной точке для любого начального приближения :

Действительно, в первом случае , т.е. для выполнения условия необходимо чтобы , но тогда . Таким образом, отображение сжатием не является.

Рассмотрим , неподвижная точка та же самая, ситуация другая. Здесь, хотя формально производная может быть довольно большой (при малых ж), однако уже на следующем шаге она будет меньше 1.

т.е. такой итерационный процесс всегда сходится.

Метод Ньютона представляет собой частный случай метода простых итераций.

Здесь нетрудно убедиться, что при существует окрестность корня, в которой .

то если корень кратности , то в его окрестности и, следовательно,.

Если — простой корень, то сходимость метода касательных квадратичная (то есть порядок сходимости равен 2).

Поскольку , то

Таким образом, сходимость метода Ньютона очень быстрая.

Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Нахождение всех корней уравнения

Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно.

Чтобы найти другие корни, можно было бы брать новые стартовые точки и применять метод вновь, но нет гарантии, что при этом итерации сойдутся к новому корню, а не к уже найденному, если вообще сойдутся.

Для поиска других корней используется метод удаления корней.

Пусть — корень функции , рассмотрим функцию. Точка будет являться корнем функции на единицу меньшей кратности, чем, при этом все остальные корни у функций и совпадают с учетом кратности.

Применяя тот или иной метод нахождения корней к функции , мы найдем новый корень (который может в случае кратных корней и совпадать с ). Далее можно рассмотреть функцию и искать корни у неё.

Повторяя указанную процедуру, можно найти все корни с учетом кратности.

Заметим, что когда мы производим деление на тот или иной корень , то в действительности мы делим лишь на найденное приближение , и, тем самым, несколько сдвигаем корни вспомогательной функции относительно истинных корней функции . Это может привести к значительным погрешностям, если процедура отделения применялась уже достаточное число раз.

Чтобы избежать этого, с помощью вспомогательных функций вычисляются лишь первые итерации, а окончательные проводятся по исходной функции , используя в качестве стартового приближения, последнюю итерацию, полученную по вспомогательной функции.

Мы рассмотрели решение уравнений только в одномерном случае, нахождение решений многомерных уравнений существенно более трудная задача.

📹 Видео

Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

10 Численные методы решения нелинейных уравненийСкачать

Решение нелинейного уравнения методом простых итераций (программа)Скачать

ЕГЭ по математике. Профильный уровень. Задание 5. Найдите корень уравненияСкачать

Метод половинного деления решение нелинейного уравненияСкачать

Метод простых итераций пример решения нелинейных уравненийСкачать

Как решают уравнения в России и СШАСкачать

Алгебра 8 класс. Уравнения с корнямиСкачать