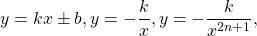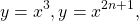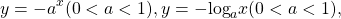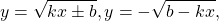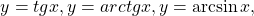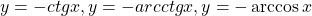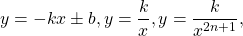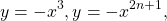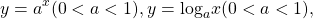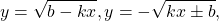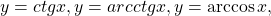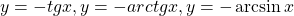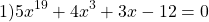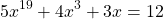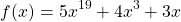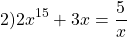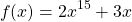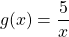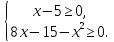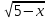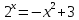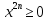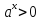Разделы: Математика
Цели:
Задачи:
Оборудование: карточки с заданиями для каждого ученика.
Организационный момент: сообщить тему урока, сформулировать цели урока.
Проводится фронтальный опрос учащихся:
- Какие функции называются возрастающими (убывающими)?
- Какие функции называются монотонными?
- Какие свойства монотонных функций вы знаете?
Свойство 1. Если y=g(x) – монотонно возрастает на промежутке I и y=f(x) – монотонно возрастает на промежутке I, то y=g(x)+f(x) – монотонно возрастает на промежутке I.
Свойство 2. Если y=f(x) возрастает (убывает) на промежутке I, то уравнение f(x)=a имеет на I не более одного корня.
Свойство 3. Если y=f(x) возрастает на I, а y=g(x) убывает на I, то уравнение f(x)=g(x), имеет не более одного корня.
II. Решение уравнений
( Этот этап урока проходит в форме беседы учителя с учениками. Ученики, основываясь на прошлом опыте решения уравнений, предлагают свои решения. Учитель показывает им более рациональные способы решения этих уравнений)
Пример 1. Решите уравнение: x 5 +x 3 +2x-4=0.
Решение: Функция f(x)=x 5 +x 3 +2x-4 возрастает как сумма трех возрастающих функций y=x 5 , y=x 3 и y=2x-4 на R.
Тогда уравнение f(x)=0 имеет не более одного корня. Испытывая делители свободного члена, находим, что x=1.
Пример 2. Решите уравнение 
Решение: Функция 


Учащимся предлагается решить это уравнение дома с помощью возведения в квадрат лавой и правой частей уравнения, и убедится что решение будет очень громоздким.
Пример 3. Решите уравнение log2(x+2)=1-x.
Решение: Функция y=log2(x+2) – возрастает на (-2; +


Непосредственно проверкой убедимся, что x=0 является корнем этого уравнения.
Каким еще способом можно решить это уравнение? (графически)
Пример 4. Определите число корней уравнения 
Решение: Рассмотрим функцию 


4, где x


Т.е. при a4 уравнение имеет единственное решение, при a 5 +3x=4.
Решить уравнение 
II. Вариант:
- Решить уравнение
.
- Решить уравнение x 5 +7x=-8.
Решить уравнение 
IV. К доске приглашаются ученики из обоих вариантов и показывают решение уравнений
V. Подведение итогов урока и выставление оценок
VI. Задание на дом
- Определить число корней уравнения
.
- Решить уравнение x 5 +2x 3 +3=54.
[1] В.В. Локоть. Применение свойств функций, преобразование неравенств // АРКТИ, Москва 2007 г.
[2] Ю.Н. Макарычев. Дополнительные главы к школьному учебнику 9 класс // Просвещение, 1998 г.
[3] И.Я. Виленкин. Алгебра и математический анализ 10 // Просвещение, 1998 г.
[4] Е.Д. Кулакин. 3000 конкурсных задач по математике // Москва 2002 г.
Видео:Математический анализ, 12 урок, Монотонность и экстремумы функцииСкачать

Решение уравнений с помощью монотонности функций
Решение уравнений с помощью монотонности функций позволяет быстро и просто найти корень уравнения (либо доказать, что уравнение корней не имеет).
Использование возрастания и убывания функций при решении уравнений опирается на следующие теоремы.
1) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)).
2) Если на некотором промежутке функция f(x) возрастает, а функция g(x) убывает (либо наоборот), то уравнение f(x)=g(x) на этом промежутке имеет единственный корень либо не имеет корней.
Доказав, что уравнение имеет на промежутке не более чем один корень, можно попытаться определить его подбором.
Если функция имеет несколько промежутков возрастания и убывания, каждый из них следует рассмотреть отдельно.
Сумма возрастающих функций — возрастающая функция. Сумма убывающих функций — убывающая функция.
Прибавление или вычитание постоянной величины не влияет на монотонность функции. Если к возрастающей функции прибавить (или вычесть) постоянную величину, получим возрастающую функцию. Если к убывающей функции прибавить (или вычесть) постоянную величину, получим убывающую функцию.
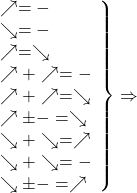
Таким образом, использование монотонности функций при решении уравнений схематически можно изобразить так:
то уравнение имеет единственный корень или не имеет корней.
Разумеется, количество слагаемых может быть больше двух.
Некоторые функции, возрастающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения (k>0, b≥0, n — целое):
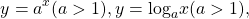
Некоторые функции, убывающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения:
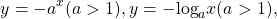
Примеры решения уравнений с помощью использования монотонности функций.
Перепишем уравнение в виде
является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.
На промежутке (-∞;0) функция
— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x= -1.
Аналогично, на промежутке (0:∞)
— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x=1.
В алгебре решение уравнений с применением возрастания и убывания функций чаше всего используется при решении иррациональных, логарифмических, показательных уравнений. Полезно взять на вооружение этот удобный и быстрый способ.
2 комментария
Добрый день. Вот это схематическое изображение монотонности очень интересно, но там не все понятно. Что вы подразумеваете под знаками равно и минус? И вот это: сумма убывающих_возрастающая? Буду благодарна комментариям
Елена, «=» — знак равенства между левой и правой частями уравнения.
Сумма убывающих функций — убывающая функция. Соответственно, одна часть уравнения — убывающая функция, а другая — возрастающая, то применима вторая теорема.
Аналогично, сумма возрастающих функций есть возрастающая функция. Если с одной стороны — возрастающая функция, с другой — убывающая, можем применить первую теорему.
Если к монотонно возрастающей функции прибавить число (или вычесть), то это никак не повлияет на её монотонность (это наглядно можно продемонстрировать графически: график функции y=f(x)±b получен из графика y=f(x) параллельным переносом на b единиц вверх или вниз вдоль оси Oy). Поэтому, если в одной части уравнения — монотонно возрастающая функция ± число, а в другой — монотонно убывающая функция, можем применить теорему два. И т.д.
Видео:монотонность функции решение уравненийСкачать

Применение свойств функций для решения уравнений
В работе рассматриваются сособы решения уравнений с использованием свойств и характеристик функций: монотонности, ограниченности, области определенийи области значений функции.
Просмотр содержимого документа
«Применение свойств функций для решения уравнений»
II. Применение свойств функций для решения уравнений
Использование ОДЗ для решения уравнений .………….. 2стр
Монотонность функции и наличие корней уравнении…. 3стр
Используемая литература………………………………………. 10 стр
Найти и освоить приемы решения уравнений способами, позволяющими значительно сократить время нахождения корней уравнений.
В ходе сбора и изучения информации по данной теме, были найдены и изучены рациональные приемы решения уравнений с применением свойств монотонности, ограниченности функций, а также области определения и значений функций, позволяющие эффективно (практически устно) решать некоторые виды уравнений, рассмотренных в качестве примеров в нашей работе.
В наших школьных учебниках алгебры в основном изучаются такие методы и приемы решения уравнений как возведение в степень, замена переменной, применение тождественных преобразований, Но использование этих способов при решении некоторых видов уравнений приводит к довольно долгим и сложным преобразованиям, особенно если уравнения в левой и правой части которой находятся функции, имеющие различную природу.
В ходе наших поисков мы познакомились с одним из эффективных способов решения уравнений вида f(x)=g(x), который и демонстрируем в нашей работе. Это способ решения уравнений с использованием свойств функций.
Начнем с уравнений, которые можно решить, используя область определения функции или область допустимых значений переменной. Напомним, что множество значений переменной, при которых обе части данного уравнения (или неравенства) имеют смысл называют областью допустимых значений уравнения или неравенства. Рассмотрим такие уравнения, которые можно решить просто найдя ОДЗ.
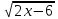
Пусть f(x) = 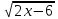
Значит правая часть уравнения должна быть неотрицательной, т.е. должно выполнятся условие 3−x ≥ 0, тогда x ≤ 3. Определяется системой двух неравенств: x≥3 и x ≤ 3. Получаем, что ОДЗ уравнения: х=3.Легко видеть, что 3 будет корнем исходного уравнения.
Приведем еще один пример уравнения:
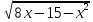
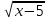
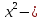
Решение: Найдем ОДЗ, решив систему неравенств
Решая неравенства этой системы получим 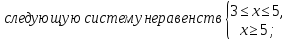
Монотонность функции и наличие корней уравнения.
Рассмотрим как применяются такое свойство функции как монотонность. Для успешного решения уравнения этим способом необходимо знать следующие утверждения: 1) если функция f (х) на некотором промежутке возрастает, а функция g(х) убывает на этом же промежутке, то уравнение f(х) = g(х) имеет на этом промежутке не более одного корня; 2) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)). Применение свойства продемонстрируем на следующих примерах:
1) x 1991 +1 =
1) В левой части этого уравнения стоит возрастающая функция на на R
в правой – убывающая на (-∞;5].
Если уравнение и будет иметь корень, то только на промежутке (-∞;5]. Легко заметить, что этот корень 1, и он, согласно теореме, единственный.
2) 5x 19 + 4x 3 +3х=12. Функция, стоящая в левой части уравнения является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.
3) 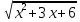
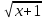
4) 2 x 15 + 3x=5/х. Функция f(x) = 5/х на каждом из промежутков (-∞;0) и (0:∞) убывает, а функция g (х) = 2 x 15 + 3x возрастает на каждом из них, поэтому наше уравнение на каждом из этих промежутков имеет не более одного корня. Убеждаемся, что это числа 1 и -1.
5) 2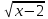
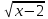
6) найти положительные корни уравнения
Функция 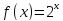
Убывает на промежутке [ 0; ∞). Следовательно, на промежутке [ 0; ∞) уравнение имеет не более одного корня. Подбором находим что х =1.
Функция 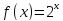
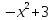
Рассмотрим, как можно применить к решению уравнений такое свойство функции как ограниченность. Метод, с помощью которого решаются уравнения с применением ограниченности функции, получил название метода мажорант. Ну, а само название метода происходит от французского слова majorer — объявлять большим. Мажорантой данной функции f(х) на множестве Р, называется такое число М, что либо f(х) ≤ М для всех х ϵ Р, либо f(х) ≥ М для всех х ϵ Р. Основная идея метода состоит в следующем: Пусть имеется уравнение f(х) = g(х) и существует такое такое число М, что для любого х из области определения f(х) и g(х) имеем f(х) ≤ М и g(х) ≥ М. Тогда уравнение f(х) = g(х) равносильно системе 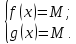
1. 
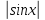
2. -1≤cosx≤1 или 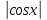
3.
4.

6.

1) Решим уравнение: + =0.
4и 10 степени – это четные числа, значит и при любом значении x. Тогда наше уравнение будет равносильно системе уравненийПервое уравнение имеет единственный корень – это число3, значит, если система и будет иметь решение, то не более одного. Проверкой убеждаемся, что3 является корнем и второго уравнения системы, а следовательно и исходного уравнения.
Заменим левую часть уравнения логарифмом, используя свойство разности логарифмов:
Представим дробь в виде , и используя неравенство Коши оценим подлогарифмическое выражение. Получаем (x + ) ≥ 4, а значит
log2 (x + ) ≥ 2. Таким образом, левая часть уравнения не меньше 2.
Рассмотрим правую часть уравнения. В правой части содержится квадратный трехчлен, поэтому выделив из него квадрат двучлена приходим к выводу, что данное выражение принимает значения не больше 2:
4 x – x 2 – 2 = – x 2 + 4 x – 2 = – ( – 4 x + 4 – 2) = – (x — 2) 2 + 2 = 2 – ( x — 2) 2
Получили, что правая часть уравнения не больше 2, т.к. (x — 2) 2 ≥ 0 при любых х. Значит, равенство левой и правой частей уравнения достигается, если они одновременно равны 2.
Из первого уравнения системы находим корень х = 2. Убеждаемся, что этот корень удовлетворяет и второму уравнению системы. Следовательно, решением исходного уравнения будет х = 2.
3) Решить уравнение:
В левой части уравнения стоит тригонометрическая функция, а в правой – сумма показательных. Формул, позволяющих находить корни в таких случаях, не существует. Оценим каждую из частей уравнения. Очевидно, что левая часть уравнения не больше 2. И так как
Поскольку 0, то причем равенство достигается только при x = 0. В данном случае
Получили, что левая часть уравнения не больше двух, а правая часть – больше или равняется двум. Таким образом, уравнение имеет решение, только если имеет решение система уравнений:
Проверкой убеждаемся, что x=0 – корень уравнения: . Значит число 0 – корень исходного уравнения. Получили ответ: x = 0.
Рассмотрим решение еще одного уравнения:
Рассмотрим две функции
Уравнение имеет решение, если наибольшее значение функции f(х) равно наименьшему значению функции g(х). Таким образом, уравнение имеет решение, только если обе части равны 2. И наше уравнение равносильно системе:
Решим первое уравнение системы:
Подставив данный корень во второе уравнение системы, получим верное равенство. Значит, решением исходного уравнения будут числа вида .
Функция y= (квадратичная функция) имеет наименьшее значение при , равное y(2)=4
Функция у= является возрастающей и, следовательно, принимает наименьшее значение при x=2
Правая часть уравнения, в силу ограниченности функции принимает значения не больше 2, поэтому исходное уравнение равносильно системе:
Так как 2-корень первого уравнения, то убедимся, что число 2-корень второго уравнения. Получаем:
Таким образом, 2-корень исходного уравнения.
Рассмотренные нами примеры могли быть решены и другими методами, но традиционные методы в данных конкретных примерах достаточно трудоемки. В нашей работе мы постарались продемонстрировать применение некоторых нестандартных приемов решения уравнений, основанных на свойствах и характеристиках функций. Планируем продолжить изучение нетрадиционных и эффективных приемов решения уравнений.
🔥 Видео
Три уравнения на одну идею. Используем монотонность функций Алгебра 10-11Скачать

Исследование функции на монотонность и экстремумыСкачать

Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Монотонность функции | МатематикаСкачать

Параметр. Серия 5. Что такое монотонная функция и как с ее помощью решать задачиСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Промежутки монотонностиСкачать

АЛГЕБРА 9 класс. Возрастающая и убывающая функцииСкачать

Промежутки монотонности функции.Скачать

Исследовать функцию на монотонность. (Пример от bezbotvy)Скачать

АЛГЕБРА С НУЛЯ — Точки Экстремума ФункцииСкачать

Свойства функции. Промежутки возрастания и убывания функции. 10 класс.Скачать

Мини-Лекция №5 Олимпиады OlimpWay по математике 2019 (Монотонность функции)Скачать

Как найти область определения функции? #shortsСкачать

Математика без Ху!ни. Непрерывность функции, точки разрыва.Скачать

Возрастание. Убывание. Increasing and Decreasing FunctionsСкачать

Как решать сложные параметры с помощью монотонности?🔥 Все полезные методы😍Скачать

Алгебра 10 класс. 9 сентября. Исследование функции на монотонность, используя свойства числовых неСкачать


 .
. .
.