Как найти модуль ускорения из уравнения

В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Что такое ускорение?

Максимально полное определение этой кинематической характеристики можно привести следующее: ускорение — это величина, показывающая быстроту изменения скорости во времени. Речь идет об изменении как модуля, так и направления. Математически ускорение вычисляют так:

Вам будет интересно: Смоленский государственный институт искусств: факультеты, специальности, сроки обучения, документы для поступления

Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:

a = (v2 — v1)/(t2 — t1).

Где v2 и v1 — скорости в моменты времени t2 и t1 соответственно.

Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с2). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.

Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

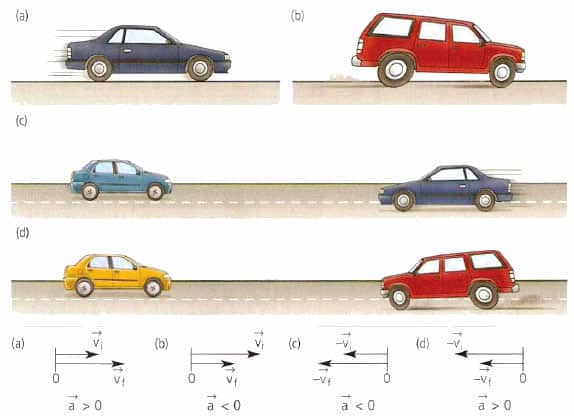
Движение по прямой и ускорение

Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.

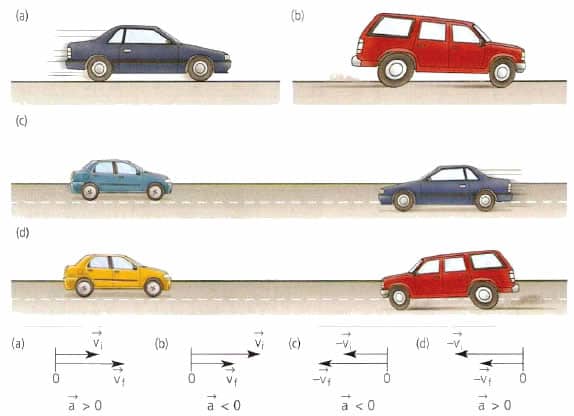
В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:

Здесь v0 — некоторая начальная скорость тела, которая может быть также равна нулю, l — пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак — — о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:

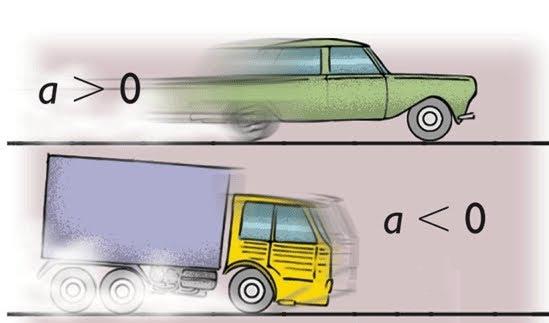
Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с2).

Видео:Центростремительное ускорение. 9 класс.Скачать

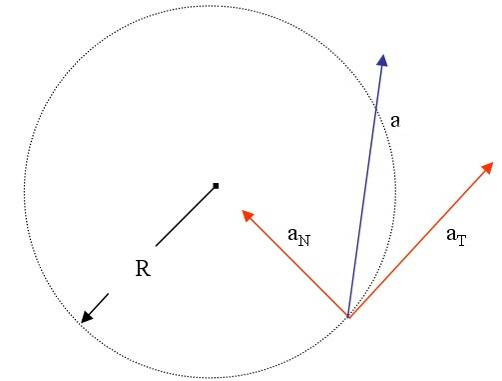
Полное ускорение и его компоненты при движении тела по кривой

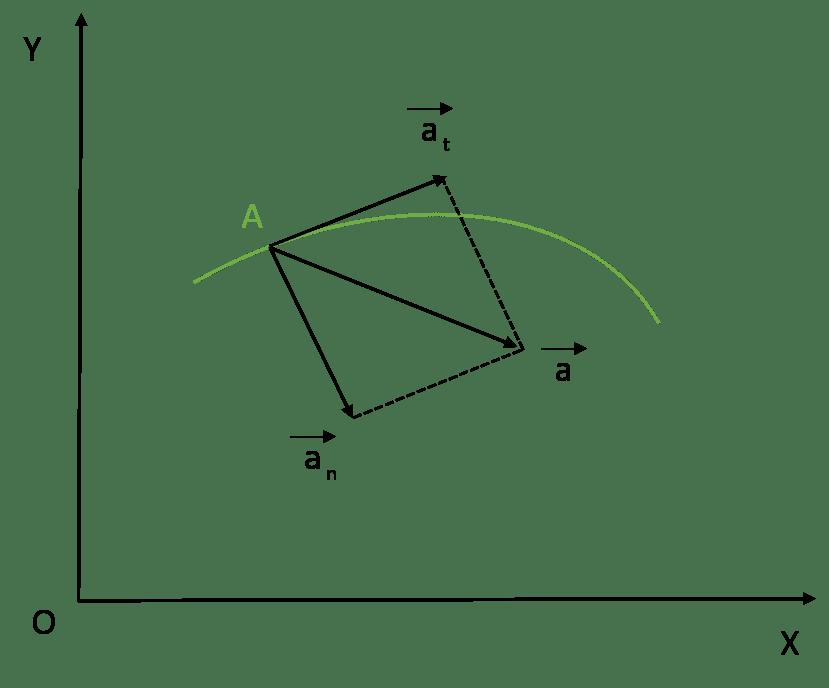
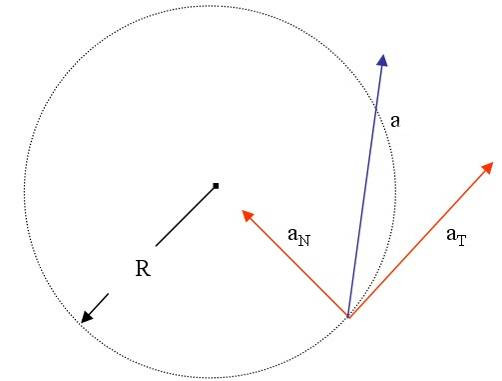
В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным at и нормальным an ускорениями. Для такого случая формула модуля ускорения точки принимает вид:

Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:

Здесь r — радиус кривизны траектории, который в случае вращения по окружности совпадает с радиусом последней.

Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина at может быть равна нулю, что является справедливым для равномерного вращения тел.

Видео:УСКОРЕНИЕ 9 класс физика Перышкин движение с ускорениемСкачать

Угловое ускорение

Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:

Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.

Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:

Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента at линейно возрастает при увеличении радиуса кривизны r.

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Пример решения задачи

Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:

Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.

Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:

at = dv/dt = 6*t + 6*t2 = 6*3 + 6*9 = 76 м/с2.

Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с2).

Нормальная компонента вычисляется так:

an = v2/r = 1/r*(2 + 3*t2 + 2*t3)2 = 1/0,2*(2+27+54)2 = 34445 м/c2.

Теперь можно рассчитать полное ускорение. Оно будет равно:

a = √(at2 + an2) = √(76 2 + 34445 2) = 34445,1 м/с2.

То есть, полное ускорение практически полностью образовано нормальной компонентой.

Наконец, ускорение угловое определяется по формуле:

α = at/r = 76/0,2 = 380 рад/с2.

Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.

Видео:РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Формулы модуля ускорения для прямолинейного и криволинейного движения. Пример решения задачи

В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.

Видео:Физика Найдите модуль ускорения тела массой 2,5 кг под действием четырех приложенных к нему силСкачать

Что такое ускорение?

Максимально полное определение этой кинематической характеристики можно привести следующее: ускорение — это величина, показывающая быстроту изменения скорости во времени. Речь идет об изменении как модуля, так и направления. Математически ускорение вычисляют так:

Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:

Где v₂ и v₁ — скорости в моменты времени t₂ и t₁ соответственно.

Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с 2 ). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с 2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.

Видео:Как найти проекцию вектора скорости и ускорения. Выполнялка 112Скачать

Движение по прямой и ускорение

Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.

В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:

Здесь v₀ — некоторая начальная скорость тела, которая может быть также равна нулю, l — пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак — — о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:

Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с 2 ).

Видео:Уравнение с модулемСкачать

Полное ускорение и его компоненты при движении тела по кривой

В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным a_t и нормальным a_n ускорениями. Для такого случая формула модуля ускорения точки принимает вид:

Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:

Здесь r — радиус кривизны траектории, который в случае вращения по окружности совпадает с радиусом последней.

Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина a_t может быть равна нулю, что является справедливым для равномерного вращения тел.

Видео:МОДУЛЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Угловое ускорение

Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:

Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.

Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:

Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента a_t линейно возрастает при увеличении радиуса кривизны r.

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Пример решения задачи

Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:

Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.

Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:

Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с 2 ).

Нормальная компонента вычисляется так:

a_n = v 2 /r = 1/r*(2 + 3*t 2 + 2*t 3 ) 2 = 1/0,2*(2+27+54) 2 = 34445 м/c 2 .

Теперь можно рассчитать полное ускорение. Оно будет равно:

То есть, полное ускорение практически полностью образовано нормальной компонентой.

Наконец, ускорение угловое определяется по формуле:

Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.

Видео:Найдите модуль ускорения A груза массой М = 30 кг. в системе, изображённой на рисунке - №31090Скачать

Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Видео:МодульСкачать

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Видео:Решение графических задач на равномерное движениеСкачать

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Видео:ЕГЭ по физике. Задание 1. Определение проекции ускоренияСкачать

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Видео:Урок 330. Скорость и ускорение при гармонических колебанияхСкачать

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Видео:Физика.Решение задач.Выполнялка 1Скачать

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Видео:ЧТО ТАКОЕ МОДУЛЬ ЧИСЛА? #shorts #егэ #огэ #математика #профильныйегэСкачать

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

🌟 Видео

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Уравнения с модулем. Что такое модуль числа. Алгебра 7 класс.Скачать