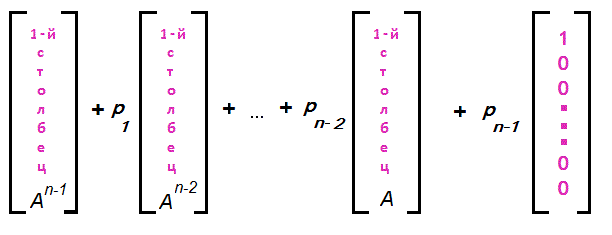Как найти матрицу по характеристическому уравнению

Характеристический полином матрицы A , вычисляется следующим образом:

| A &#x2212 &#x03BB E |

где E — единичная матрица, размеры которой совпадают с размерами исходной матрицы A .

Разберем подробнее приведенную выше формулу. Если матрица A задана в виде:

тогда выражение A &#x2212 &#x03BB E имеет вид:

Наконец, нам нужно найти определитель:

Раскрыв этот определитель, мы получим полином n -ой степени ( n — порядок исходной матрицы), зависящий от &#x03BB :

P &#x2006 ( &#x03BB ) = c _n &#x03BB &#x2006 n + c _{n &#x2212 1} &#x03BB &#x2006 n &#x2212 1 + . + c _i &#x03BB &#x2006 i + . + c ₁ &#x03BB &#x2006 + c ₀

Поскольку для вычисления характеристического полинома, требуется нахождение определителя матрицы, то характеристический полином может быть найден только для квадратной матрицы.

Наш онлайн калькулятор находит характеристический полином матрицы, причем в качестве элементов матрицы, можно вводить не только числа и дроби, но и параметры.

Видео:Решение матричных уравненийСкачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:Собственные значения матрицыСкачать

Характеристический полином, собственные числа, собственные векторы матрицы

В настоящем разделе $ n_ $ означает порядок квадратной матрицы $ A_ $.

Видео:Собственные векторы и собственные значения матрицыСкачать

Характеристический полином

определяется для произвольной квадратной матрицы $ A_ $ как 1) $ det (A_-lambda E) $, где $ E_ $ – единичная матрица одинакового с $ A_ $ порядка.

Пример. Для $ n=2_ $:

Теорема 1.

Пример. Характеристический полином матрицы Фробениуса

$$ mathfrak F= left( begin 0 & 1 & 0 & 0 & dots & 0 & 0 \ 0 & 0 & 1 & 0 & dots & 0 & 0 \ 0 & 0 & 0 & 1 & dots & 0 & 0 \ vdots& &&&ddots & & vdots \ 0 & 0 & 0 & 0 & dots & 0 & 1 \ a_n & a_ & a_ & & dots & a_2 & a_1 end right)_ $$ равен $ (-1)^n(lambda^n-a_1lambda^-dots-a_) $.

Видео:Характеристическое уравнение в ДУСкачать

Характеристический полином линейного оператора

определяется как характеристический полином матрицы этого оператора в произвольном базисе линейного пространства, в котором этот оператор задан. Подробнее ☞ ЗДЕСЬ.

Видео:Пример действий над матрицами (4): многочлен от матрицы.Скачать

Характеристический полином линейного однородного разностного уравнения

$ n_ $-го порядка $$ x_=a_1 x_+ dots+ a_n x_K, quad a_n ne 0, $$ определяется как $$ lambda^n — a_1 lambda^ — dots — a_n . $$ Подробнее ☞ ЗДЕСЬ.

Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Свойства

Теорема 2. Характеристический полином матрицы не меняется

1. при ее транспонировании: $$ det (A-lambda E) = det (A^-lambda E_) , ;$$ 2. при переходе к подобной матрице: если $ B=C^AC^ $ при произвольной неособенной матрице $ C_ $, то $$ det (A-lambda E) equiv det (B-lambda E_) , . $$

Теорема 3. Пусть матрица $ A_ $ имеет порядок $ mtimes n_ $, а $ B_ $ — порядок $ ntimes m_ $. Тогда эти матрицы допускают умножение в любом порядке, т.е. определены $ AB_ $ и $ BA_ $ и оба произведения будут квадратными матрицами — порядков $ m_ $ и $ n_ $ соответственно. Тогда характеристические полиномы этих произведений различаются лишь на степень $ lambda_ $:

$$ lambda^n det (AB — lambda E_)equiv lambda^m det (BA — lambda E_) . $$

Если матрицы $ A_ $ и $ B_ $ — квадратные одинакового порядка, то характеристические полиномы матриц $ AB_ $ и $ BA_ $ тождественны.

Теорема 4. Если характеристический полином матрицы $ A_ $ равен

$$ f(lambda)=(-1)^n lambda^n+a_1lambda^+dots+a_lambda+a_n $$ и $ a_ ne 0 $, то характеристический полином матрицы $ A^_ $ равен $$ f^(lambda)=frac f(1/lambda) = frac left[ (-1)^n+a_1 lambda + dots+ a_lambda^+a_nlambda^ right] . $$

Видео:Характеристический многочлен. ТемаСкачать

Теорема Гамильтона-Кэли

Теорема 5. Результатом подстановки в характеристический полином $ det (A_-lambda E) $ самой матрицы $ A_ $ будет нулевая матрица:

$$ det (A-lambda E)= (-1)^n lambda^n +a_1 lambda^+dots+a_lambda+ a_n Rightarrow $$ $$ Rightarrow (-1)^n A^n +a_1 A^+dots+a_A+ a_n E = _ . $$

матрица является корнем своего характеристического полинома.

Доказательство ☞ ЗДЕСЬ.

Пример. Для $ n_=2 $:

$$ left(begin a_ & a_ \ a_ & a_ end right)^2 — (a_+a_)left(begin a_ & a_ \ a_ & a_ end right) + (a_a_-a_a_) left(begin 1 & 0 \ 0 & 1 end right) = left(begin 0 & 0 \ 0 & 0 end right) . $$

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Собственное число

определяется для квадратной матрицы $ A_ $ как произвольный корень ее характеристического полинома $ det (A_-lambda E) $. Набор всех собственных чисел матрицы $ A_ $ (с учетом их кратностей) называется спектром матрицы (таким образом спектр матрицы $ A_ $ порядка $ n_ $ всегда состоит из $ n_ $ чисел, часть из которых могут быть одинаковыми). Максимальный из модулей собственных чисел матрицы $ A_ $ называется ее спектральным радиусом, он иногда обозначается $ rho(A) $.

Пример. Найти спектр матрицы

$$ A= left(begin 0&1&2&3\ -1&0&4&7\ -2&-4&0&2\ -3&-7&-2&0 endright). $$ Решение. Характеристический полином $$ det (A-lambda E)=left|begin -lambda&1&2&3\ -1&-lambda&4&7\ -2&-4&-lambda&2\ -3&-7&-2&-lambda endright|=lambda^4+ 83lambda^2 $$ имеет корни $ lambda_1=0, lambda_2 = sqrt, lambda_3 = — sqrt $, причем $ lambda_ $ — второй кратности.

Ответ. Спектр матрицы $ A_ $: $ <0,0, sqrt,- sqrt > $. Спектральный радиус матрицы $ A_ $: $ rho(A)= sqrt $.

Теорема 6. Если $ <lambda_,lambda_,dots,lambda_ > $ — спектр матрицы $ A_ $, то

$$ lambda_1+lambda_+dots+lambda_n = operatorname(A)=a_+a_+dots+a_, $$ $$ lambda_1cdotlambda_times dots times lambda_n = (-1)^ndet (A) . $$

Доказательство следует из представления характеристического полинома через миноры матрицы и формул Виета. ♦

Для того, чтобы матрица $ A_ $ была неособенной необходимо и достаточно, чтобы среди ее собственных чисел не было нулевого.

Теорема 7. Пусть $ g(x)=b_x^m+dots+b_m in [x] $ — произвольный полином. Вычислим полином от матрицы $ A_ $:

$$ g(A)=b_A^m+dots+b_m E , . $$ Тогда если $ <lambda_,dots,lambda_ > $ — спектр матрицы $ A_ $, то $ <g(lambda_),dots,g(lambda_n) > $ — спектр матрицы $ g(A_) $.

Результат теоремы обобщается и на более широкий класс функций $ g_(x) $ — фактически на любую функцию, которая, вместе со своими производными, может быть определена на спектре матрицы $ A_ $. В частности, если $ det A_ ne 0 $, то спектр матрицы $ A^_ $ совпадает с $ _^n $.

Имеет место следующее равенство, связывающее степени матрицы $ A_ $ с суммами Ньютона ее характеристического полинома:

$$ operatorname(A^k)=lambda_1^k+dots+lambda_n^k . $$ Здесь $ operatorname_ $ обозначает след матрицы (т.е. сумму ее диагональных элементов). Утверждение остается справедливым и для отрицательных показателей $ k_ $ при условии, что $ det A_ ne 0 $.

Имеет место следующее равенство:

$$ det g(A) = (-1)^ (f,g_) , $$ где $ (f,g_) $ означает результант полиномов $ f(x) =det (A-x_ E) $ и $ g_(x) $.

Теорема 8. Собственные числа вещественной симметричной матрицы $ A_ $ все вещественны.

Доказательство ☞ ЗДЕСЬ.

Теорема 9. Собственные числа вещественной кососимметричной матрицы $ A_ $ все мнимы, за исключением, возможно, $ lambda_ = 0 $.

Доказательство ☞ ЗДЕСЬ.

Теорема 10. Собственные числа вещественной ортогональной матрицы все равны $ 1_ $ по абсолютной величине (модулю). Характеристический полином ортогональной матрицы является возвратным если $ +1 $ не является его корнем или является корнем четной кратности. Хотя бы одно собственное число ортогональной матрицы нечетного порядка равно $ +1 $ или $ (-1) $.

Доказательство ☞ ЗДЕСЬ.

Теорема 11. Спектр циклической матрицы

$$ left(begin a_1 & a_2 & a_3 & dots & a_n \ a_n & a_1 & a_2 & dots & a_ \ a_ & a_n & a_1 & dots & a_ \ vdots & & & & vdots \ a_2 & a_3 & a_4 & dots & a_1 end right) . $$ совпадает с набором чисел $$ <f(1),f(varepsilon_1), dots, f(varepsilon_) > ,$$ при $$ f(x)=a_+a_2x+a_3x^2+dots+a_nx^ $$ и $$ varepsilon_k=cos frac + sin frac $$ — корне n-й степени из единицы.

Доказательство ☞ ЗДЕСЬ.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Локализация собственных чисел

Теорема 12. [1]. Собственные числа матрицы являются непрерывными функциями ее элементов. Иначе: пусть

$$A=left[a_ right]_^n quad , quad B=left[b_ right]_^n . $$ Обозначим $$M= max_<j,kin> left <|a_|, |b_ | right> quad , quad delta = fracsum_^n |a_ — b_ | . $$ Тогда любому собственному числу $ lambda_^ $ матрицы $ A_ $ можно поставить в соответствие такое собственное число $ mu_^ $ матрицы $ B_ $, что $$ |lambda_-mu_ | le (n+2) M sqrt[n] . $$

Собственно факт непрерывной зависимости собственных чисел от элементов матрицы следует из представления характеристического полинома из теоремы ☞ ПУНКТА — коэффициенты этого полинома полиномиально (и, следовательно, непрерывно) зависят от элементов матрицы. Далее используем теорему о непрерывной зависимости корней полинома от его коэффициентов.

Выясним теперь на примере, насколько малым может быть возмущение элементов матрицы чтобы сохранились хотя бы количество вещественных корней ее характеристического полинома.

Пример [Уилкинсон] [2]. Найти собственные числа матрицы

$$ A= left( begin 20 & 20 & & & & \ & 19 & 20 & & & \ & & 18 & 20 & & \ & & & ddots & ddots & \ & & & & 2 & 20 \ <colorvarepsilon > & & & & & 1 \ end right)_ $$ при $ <colorvarepsilon >=10^ $ (все неуказанные элементы матрицы считаются равными нулю).

Решение. Характеристический полином $$ det(A-lambda E) = prod_^ (j-lambda) — 20^ <colorvarepsilon > = $$ $$ =lambda^-,lambda^+,lambda^-, lambda^ +, lambda^-, lambda^+ , lambda^-, lambda^+ $$ $$ +, lambda^ — , lambda^ +, lambda^-, lambda^9 + $$ $$ +, lambda^8 — , lambda^7+, lambda^6 -, lambda^5 +, lambda^4- $$ $$ -, lambda^3 +, lambda^2 -,lambda + $$ очень похож на полином из другого ☞ ПРИМЕРА Уилкинсона. Он имеет корни $$ lambda_1=0.995754, lambda_2=2.109241, lambda_3=2.574881, $$ $$ lambda_=3.965331pm 1.087735, mathbf i, lambda_=5.893977pm 1.948530 , mathbf i, $$ $$ lambda_=8.118073 pm 2.529182 , mathbf i, lambda_=10.5pm 2.733397 , mathbf i, $$ $$ lambda_=12.881926pm 2.529182 , mathbf i, lambda_=15.106022 pm 1.948530 , mathbf i, $$ $$ lambda_=17.034669pm 1.087735 , mathbf i, $$ $$ lambda_=18.425118, lambda_=18.890758, lambda_=20.004245 . $$ Итак, нановозмущение 2) в одном-единственном элементе матрицы приводит к существенному изменению спектра: из $ 20 $ вещественных собственных чисел «остаются в живых» только $ 6_ $; кроме того, у образовавшихся мнимых корней оказываются достаточно большими мнимые части. В данном примере допустимые возмущения для $ <colorvarepsilon > $, т.е. такие, при которых сохранится свойство вещественности всех корней характеристического полинома, находятся в пределах 3) $$ -8.636174times 10^ ♦

Теорема 13 [Гершгорин]. 4) Обозначим $ mathbb D_ $ круг на комплексной плоскости $ mathbb C_ $ с центром в точке $ a_^ $ и радиуса

$$ r_j=sum_^n left|a_right| .$$ Тогда спектр матрицы $ A_ $ лежит внутри объединения этих кругов: $$ subset bigcup_^n mathbb D_j . $$ Иными словами: любое собственное число матрицы должно удовлетворять хотя бы одному из неравенств $$ |z- a_ | ☞ ЗДЕСЬ.

Согласно этой теореме, главные миноры матрицы $ A-lambda, E $ играют роль системы полиномов Штурма для характеристического полинома симметричной матрицы $ A_ $.

Если все главные миноры $ A_1,A_2,dots,A_ $ симметричной матрицы $ A_ $ отличны от нуля, то число положительных собственных чисел матрицы $ A_ $ равно числу знакопостоянств, а число отрицательных собственных чисел — числу знакоперемен в ряду $ 1,A_1,dots,A_n $:

$$ operatorname 0 > = (1,A_1,dots,A_n), $$ $$ operatorname < det (A-lambda E) =0 | lambda ненулевойстолбец $$ X_= left( begin x_^ \ vdots \ x_^ end right) in mathbb^n $$ такой, что $$ AX_=lambda_ X_ quad iff quad (A -lambda_E) X_ = mathbb O_ . $$ По определению собственного числа, $ det (A^ -lambda_E) = 0 $ и, следовательно, система однородных уравнений $ (A -lambda_E) X^ = mathbb O $ всегда имеет нетривиальное решение; более того, этих решений бесконечно много. Таким образом, одному и тому же собственному числу матрицы принадлежит бесконечное множество собственных векторов. Эту бесконечность можно описать с помощью фундаментальной системы решений (ФСР).

Пример. Найти собственные векторы матрицы

Решение. Спектр матрицы найден выше. $$(A-0 cdot E)X=mathbb O quad Longrightarrow mbox= left< _1=left(begin 4 \ -2 \ 1 \ 0 endright), _2=left(begin 7 \ -3 \ 0 \ 1 end right) right>.$$ Любой вектор вида $ alpha_ _1 + alpha_2 _2 $ будет собственным, принадлежащим $ lambda_=0 $. $$ begin (A- mathbf i, sqrt E)X=mathbb O \ \ Downarrow \ \ _3= left(begin 1- mathbf i , sqrt \ 8-2, mathbf i , sqrt \ 12 \ 17+mathbf i , sqrt endright) end qquad begin (A+mathbf i sqrt E)X=mathbb O \ \ Downarrow \ \ _4= left(begin 1+mathbf i , sqrt \ 8+2mathbf i , sqrt \ 12 \ 17- mathbf i ,sqrt endright) end . $$ ♦

Еще один способ нахождения собственного вектора основан на теореме Гамильтона-Кэли.

Теорема 15. Пусть $ lambda_^ $ — собственное число матрицы $ A_ $. Обозначим частное от деления характеристического полинома на линейный множитель $ lambda_ — lambda_ $ через $ f_(lambda)^ $:

$$ f_(lambda) equiv f(lambda) / (lambda-lambda_) . $$ Тогда любой ненулевой столбец матрицы $ f_(A)^ $ является собственным вектором, принадлежащим $ lambda_^ $.

Доказательство следует из равенства $$(A-lambda_ E)f_(A)=mathbb O_ . $$ На основании определения любой ненулевой столбец $ f_(A)^ $ должен быть собственным вектором матрицы $ A_ $. ♦

Пример. Найти собственные векторы матрицы

$$ A=left( begin 9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5 end right) . $$

Решение. $$ det (A-lambda E)=-lambda^3+ 7, lambda + 6 equiv -(lambda_-3) (lambda+2)(lambda+1) , .$$ Пренебрегая знаком – , имеем: $$ begin f_1(lambda)=lambda^2+3lambda+2 & u & f_1(A)= left( begin 40 & 80 & -20 \ 0 &0 & 0 \ 40 & 80 & -20 end right) , \ f_2(lambda)=lambda^2-2lambda-3 & u & f_2(A)= left( begin -10 & -30 & 10 \ 5 &15 & -5 \ 0 & 0 & 0 end right) , \ f_3(lambda)=lambda^2-lambda-6 & u & f_3(A)= left( begin -4 & -8 & 4 \ 4 & 8 & -4 \ 8 & 16 & -8 end right) . end $$

Если $ lambda_^ $ является простым корнем характеристического полинома 5) , то ненулевые столбцы $ f_(A)^ $ будут пропорциональными. Или, что то же, $ operatorname f_(A)^ = 1 $.

Тогда очевидно, что и строки матрицы $ f_(A)^ $ тоже должны быть пропорциональны!

Доказать, что любая ненулевая строка матрицы $ f_(A)^ $ является собственным вектором матрицы $ A^<^>_ $, принадлежащим $ lambda_^ $. Доказать, что собственный вектор матрицы $ A_ $ ортогонален собственному вектору матрицы $ A^_ $, если эти векторы принадлежат различным собственным числам 6) .

На практике вычисление полинома $ f_(lambda)^ $ может быть осуществлено с помощью схемы Хорнера.

Пример. Вычислить собственный вектор матрицы

$$ A=left( begin 23 & 75 & -92 \ 6 & 74 & 72 \ 37 & -23 & 87 end right) , $$ принадлежащий ее вещественному собственному числу.

Решение. Характеристический полином $$ f(lambda)= -lambda^3+184,lambda^2-14751,lambda+611404 $$ имеет единственное вещественное собственное число $ lambda_ approx 96.8817 $. Составляем схему Хорнера $$ begin & -1 & 184 & -14751 & 611404 \ hline 96.8817 & -1 & 87.1183 & -6310.8310 & -0.0352 end $$ За счет ошибок округления мы получили ненулевое значение для $ f(lambda_) $. В качестве частного от деления $ f(lambda) $ на $ lambda-lambda_ $ берем $$ f_(lambda)= -lambda^2 + 87.1183, lambda — 6310.8310 . $$ Подставляем в него матрицу $ A_ $ и вычисляем первый столбец матрицы $$ -A^2+87.1183,A -6310, E = left( begin -1882.1101 & * & * \ -2723.2902 & * & * \ -708.6229 & * & * end right) .$$ Проверяем: $$ left( begin 23 & 75 & -92 \ 6 & 74 & 72 \ 37 & -23 & 87 end right) left( begin -1882.1101 \ -2723.2902 \ -708.6229 end right) — 96.8817 left( begin -1882.1101 \ -2723.2902 \ -708.6229 end right)= left( begin 0.0356 \ 0 \ -0.0002 end right) . $$ ♦

Можно развить последний метод далее: найти универсальную формулу для собственного вектора как функции ее собственного числа. Действительно, найдем частное от деления характеристического полинома $$ f(lambda) =a_0lambda^n+a_0lambda^+dots+ a_n, quad a_0=(-1)^n $$ на линейный полином $ lambda- lambda_ $, где $ lambda_ $ — произвольное число из $ mathbb C $. С помощью той же схемы Хорнера, получаем $$ q(lambda)=a_0lambda^+(a_0lambda_+a_1)lambda^+(a_0lambda_^2+a_1lambda_+a_2)lambda^+dots+ (a_0lambda_^+a_1lambda_^+dots+a_) , . $$ Если $ lambda_ $ является собственным числом матрицы $ A_ $, то любой ненулевой столбец матрицы $$ q(A)= a_0A^+(a_0lambda_+a_1)A^+(a_0lambda_^2+a_1lambda_+a_2)A^+dots+ (a_0lambda_^+a_1lambda_^+dots+a_)E $$ будет собственным вектором, принадлежащим $ lambda_ $.

Пример. Найти представление всех собственных векторов матрицы

$$ A=left( begin 9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5 end right) $$ в виде функции ее собственных чисел.

Решение. Характеристический полином матрицы был вычислен выше: $ f(lambda)=-lambda^3+ 7, lambda + 6 $. Имеем, $$ q(lambda)=-lambda^2-lambda_lambda+(7-lambda_^2) $$ и $$ q(A)=-A^2-lambda_A+(7-lambda_^2)E= left(begin -lambda_^2-9lambda_-4 & -22lambda_-14 & 6lambda_+2 \ lambda_-3 & -lambda_^2+4lambda_-3 & -lambda_+3 \ -8lambda_-16 & -16lambda_-32 & -lambda_^2+5lambda_+14 end right) , . $$ Берем произвольный столбец этой матрицы, например, первый: $$ X_(lambda_)= left(begin -lambda_^2-9lambda_-4 \ lambda_-3 \ -8lambda_-16 end right) , . $$ Утверждается, что $ X_ (lambda_) $ — универсальное представление всех собственных векторов матрицы. Действительно, $$ X_(-1) = left(begin 4 \ -4 \ -8 end right), X_(-2) = left(begin 10 \ -5 \ 0 end right), X_(3) = left(begin -40 \ 0 \ -40 end right) , . $$ ♦

Теорема 16. Пусть $ g(x)=b_0x^m+dots+b_ in [x] $ – произвольный полином. Если $ X_in mathbb C^ $ — собственный вектор матрицы $ A_ $, соответствующий собственному числу $ lambda_^ $, то он же будет собственным и для матрицы $ g(A)^ $, принадлежащим собственному числу $ g(lambda_)^ $.

Доказательство. Домножим равенство $ A_=lambda_^_ $ слева на матрицу $ A_ $: $$ A^2_=lambda_A_=lambda_^2_ .$$ По индукции доказывается и общее равенство: $$ A^k_=lambda_^k_ .$$ Домножим его на $ b_^ $ и просуммируем по $ k_ $ от $ 0_ $ до $ m_ $: $$ g(A)_=g(lambda_)_ ,$$ что и доказывает утверждение теоремы. ♦

Если матрица $ A $ невырождена, то теорема остается справедливой и для произвольного полинома от $ A^ $. В частности, собственные векторы $ A^ $ совпадают с собственными векторами матрицы $ A $.

Теорема 17. Собственные векторы, принадлежащие различным собственным числам матрицы $ A_ $, линейно независимы.

Теорема 18. Собственные векторы, принадлежащие различным собственным числам вещественной симметричной матрицы $ A_ $, ортогональны, т.е. если $ mathfrak X_1 $ принадлежит собственному числу $ lambda_ $, а $ mathfrak X_2 $ принадлежит собственному числу $ lambda_ $ и $ lambda_1 ne lambda_2 $, то

$$ langle mathfrak X_1, mathfrak X_2 rangle =0 , $$ где $ langle , rangle $ означает скалярное произведение, определяемое стандартным образом: $ langle X,Y rangle =x_1y_1+dots+x_ny_n $.

Доказательство ☞ ЗДЕСЬ.

Видео:Собственные значения и собственные векторыСкачать

Теорема Перрона-Фробениуса

Теорема 19 [Перрон, Фробениус]. Для положительной матрицы $ A_ $ существует положительное собственное число $ lambda_ $ такое, что все остальные собственные числа этой матрицы меньше $ lambda_ $ по абсолютной величине (модулю). Соответствующий этому собственному числу собственный вектор может быть выбран положительным:

$$ exists mathfrak X_ > mathbb O: quad A mathfrak X_ = lambda_ mathfrak X_ . $$

Число $ lambda_ $ из теоремы называется собственным числом Перрона или собственным числом Перрона-Фробениуса матрицы $ A_ $, а соответствующий ему произвольный положительный собственный вектор — собственным вектором Перрона-Фробениуса матрицы $ A_ $.

Спектральный радиус положительной матрицы $ A_ $ совпадает с ее собственным числом Перрона-Фробениуса:

Пример. Найти собственное число и вектор Перрона-Фробениуса для матрицы

$$ A= left(begin 2 & 7 & 18 & 28 \ 1 & 8 & 2 & 8 \ 3 & 1 & 4 & 1 \ 5 & 9 & 26 & 5 end right) , . $$

Решение. Характеристический полином матрицы $ A_ $ $$ det(A-lambda E)=lambda^4-19, lambda^3-175, lambda^2-285, lambda+10390 $$ имеет корнями $$ lambda_ approx -6.260463 pm 5.452465 mathbf i, lambda_3 approx 5.878976, lambda_4 approx 25.641950 . $$ Числом Перрона-Фробениуса является $ lambda_4 $, а соответствующий ему собственный вектор Перрона-Фробениуса можно взять равным $$ left( begin 1 \ 0.365240 \ 0.184802 \ 0.634244 end right) quad mbox quad left( begin 2.737922 \ 1 \ 0.505974 \ 1.736510 end right) quad mbox left( begin 5.411185 \ 1.976383 \ 1 \ 3.432010 end right) quad mbox quad left( begin 1.576681 \ 0.575868 \ 0.291374 \ 1 end right) quad mbox quad left( begin 0.798133 \ 0.291510 \ 0.147496\ 0.506210 end right) quad mbox dots $$ (напоминаю: собственный вектор определяется с точностью до ненулевого сомножителя!). Последний вектор имеет длину равную $ 1_ $. ♦

1. Собственное число Перрона-Фробениуса всегда простое для характеристического полинома матрицы $ A_ $. Отсюда следует, что собственный вектор Перрона-Фробениуса определяется единственным образом — с точностью до домножения на положительный скаляр.

2. Любой собственный вектор положительной матрицы $ A_ $, не соответствующий собственному числу Перрона-Фробениуса, не может состоять исключительно только из положительных элементов. Иными словами, хотя бы одна компонента такого вектора должна быть либо отрицательной либо мнимой.

3. Для собственного числа Перрона-Фробениуса справедливо неравенство $$ min_<jin> sum_^n a_ le lambda_ le max_<jin> sum_^n a_ . $$

4. Собственное число Перрона-Фробениуса матрицы $ A_ $ совпадает с собственным числом Перрона-Фробениуса матрицы $ A^ $.

Какие из перечисленных свойств можно распространить на случай неотрицательных матриц ? Каждую такую матрицу можно рассматривать как предел последовательности (строго) положительных матриц. Воспользовавшись теоремой о непрерывной зависимости собственных чисел матрицы от ее элементов, можем сделать вывод, о том, что для неотрицательной матрицы $ A_ $ всегда найдется вещественное неотрицательное собственное число, которое будет являться максимальным по модулю среди всех собственных чисел матрицы. Другое дело, что в данном случае — в отличие от случая положительных матриц — такое мажорирующее собственное число может оказаться не единственным.

Пример. Спектр неотрицательной матрицы

$$ A=left( begin 0 & 1 \ 1 & 0 end right) $$ состоит из чисел $ lambda_1=+1 $ и $ lambda_1=-1 $ одинакового модуля. ♦

Однако, по-прежнему, хотя бы одно неотрицательное вещественное число $ lambda_ $ со свойством $ rho(A) = lambda_ $ существовать будет; более того, ему будет соответствовать неотрицательный собственный вектор $ mathfrak X ge mathbb O $. Это число (вектор) по-прежнему называются числом (вектором) Перрона-Фробениуса 7) матрицы $ A_ $.

Частным случаем неотрицательных матриц являются стохастические матрицы, т.е. неотрицательные матрицы, в которых сумма элементов каждой строки равна $ 1_ $: $$ P=left[p_right]_^n, <p_ge 0 >_^n, sum_^n p_ = 1 npu quad j in . $$

Теорема 20. Собственное число Перрона-Фробениуса стохастической матрицы равно $ 1_ $. Этому собственному числу соответствует собственный вектор $ X=[1,1,dots,1]^ $.

Доказательство существования собственного числа равного $ 1_ $ и соответствующего ему собственного вектора $ X=[1,1,dots,1]^ $ следует из равенства $$ P left( begin 1 \ 1 \ vdots \ 1 end right) = left( begin 1 \ 1 \ vdots \ 1 endright) . $$ Далее, из теоремы Гершгорина следует, что любое собственное число $ lambda_in mathbb C $ стохастической матрицы должно удовлетворять неравенству $$|lambda — p_|le sum_ |p_|=1-p_ $$ хотя бы при одном $ j_ $. Воспользовавшись следствием к неравенству треугольника получаем: $$|lambda| — |p_|le |lambda — p_| le 1-p_ Rightarrow |lambda| le 1 . $$ ♦

Видео:Обратная матрицаСкачать

Методы вычисления характеристического полинома

Вычисление коэффициентов характеристического полинома матрицы $ A_ $ непосредственным разложением определителя $ det (A-lambda_ E) $ на $ n!_ $ слагаемых — крайне неэффективно. Элементами этого разложения являются выражения, полиномиально зависящие от параметра $ lambda_ $. На каждом этапе вычислений мы получаем проблему символьных вычислений: хранения таких полиномов и действий над ними.

Основной метод вычисления числовых определителей — метод Гаусса — также неэффективен в приложении к вычислению определителя, элементы которого зависят от параметра. Источником вычислительных проблем является неудобное расположение переменной $ lambda_ $ — на главной диагонали матрицы. Первый же шаг метода Гаусса приводит к делению на элемент $ a_ — lambda $, и, в дальнейшем, элементы преобразованной матрицы будут уже не полиномами, а рациональными функциями относительно $ lambda_ $. Следующие шаги метода приводят к возрастанию степеней знаменателей. Необходимость в организации хранения рациональных функций и программировании действий с ними кажется тем более неоправданной, если вспомнить, что окончательный ответ — выражение для $ det (A-lambda_ E) $ — должно быть полиномом по $ lambda_ $; т.е. знаменатели дробей в конечном ответе сократятся.

А в качестве усугубляющего положение обстоятельства «на заднем плане» маячит проблема точности вычислений коэффициентов характеристического полинома — чувствительность его корней к возмущению его коэффициентов бывает весьма высокой.

Какой выход предлагается? — Предварительно преобразовать определитель $ det (A-lambda_ E) $ к виду, когда переменная $ lambda_ $ оказывается «выметенной» с диагонали на крайний ряд (в столбец или в строку). При этом допускается увеличение размеров (порядка) определителя. Такое представление дает возможность разложения определителя по этому исключительному ряду, и, тем самым, позволяет свести задачу к вычислению числовых определителей — а уж для этой задачи применение метода Гаусса вполне эффективно.

Видео:Матрицы: начало. Высшая математикаСкачать

Метод Леверье

Метод основан на формуле (см. следствие к теореме $ 7 $ ☞ ЗДЕСЬ ): $$ operatorname (A^k)=lambda_1^k+dots+lambda_n^k=s_k , $$ т.е. след $ k_ $-й степени матрицы $ A_ $ равен $ k_ $-й сумме Ньютона ее характеристического полинома $ f(lambda)=det (A-lambda E ) $. Вычисляем последовательные степени матрицы $ A_ $: $$s_1=operatorname (A), s_2=operatorname (A^2), dots, s_n=operatorname (A^n) .$$ Неизвестные коэффициенты $ f(lambda)=(-1)^n(lambda^n+a_1lambda^+ dots+a_n) $ находим по рекурсивным формулам Ньютона: $$ a_1=-s_1, a_2=-(s_2+a_1s_1)/2, $$ $$ a_k=-(s_+a_1s_+a_2s_+dots+a_s_1)/k npu k le n. $$ Очевидно, что не имеет смысла вычислять все элементы матрицы $ A^ $ — достаточно обойтись лишь элементами ее главной диагонали.

Пример [Леверье]. Найти характеристический полином матрицы

$$ A=left(begin -5.509882&1.870086&0.422908&0.008814 \ 0.287865&-11.811654&5.711900&0.058717 \ 0.049099&4.308033&-12.970687&0.229326 \ 0.006235&0.269851&1.397369&-17.596207 end right) . $$

Решение. $$ A^2=left(begin 30.91795128&-30.56848188&2.878480155&0.0031325713\ -4.705449283&164.6764010&-141.3504639&-0.4143169528\ 0.3341843103&-106.6094396&193.1869924& -6.756396001\ 0.0022236138&-1.904168948&-41.16923134& 309.9628536 end right), $$ $$ A^3=left(begin -179.0125092&431.2849919&-198.8601505& -0.9173897610\ 66.38829278&-2562.954533& 2771.458834& -15.49709921\ -23.08728044&2090.291485&-3124.010318& 156.9329019\ -0.649145142&-71.21907809&956.2502143& -5463.723497 end right), $$ $$ A^4=left(begin 1100.720103& ast& ast& ast \ ast& 42332.23816& ast& ast \ ast& ast& 52669.62534& ast \ ast& ast& ast& 96355.91518 end right) . $$ Вычисляем следы матриц: $$s_1=-47.888430, s_2=698.7441983, s_3=-11329.70086, s_4= 192458.4988 ,$$ и по формулам Ньютона получаем: $$a_1= 47.888430, a_2 = 797.278764_ , a_3 = 5349.45551_, a_4 = 12296.550_ . $$ ♦

После нахождения коэффициентов характеристического полинома можно найти его корни каким-либо 8) методом. Если $ lambda_^ $ — одно из собственных чисел, то для нахождения соответствующего собственного вектора воспользуемся алгоритмом из ☞ ПУНКТА. Предположив дополнительно, что это собственное число простое 9) , обозначим $$ f_(lambda)= f(lambda)/(lambda-lambda_)=(-1)^n(lambda^ +p_1lambda^+dots+p_lambda+p_) $$ т.е. частное от деления $ f(lambda_) $ на $ lambda-lambda_ $. Тогда любой ненулевой столбец матрицы $ f_(A)^ $ будет собственным вектором, принадлежащим $ lambda_^ $. Как правило, собственным вектором можно взять комбинацию

Степени матрицы $ A_ $ уже нами посчитаны при вычислении коэффициентов характеристического полинома.

Пример. Для приведенного выше примера находим собственные числа:

$$ lambda_1=-17.86326, lambda_2=-17.15242, lambda_3=-7.57404, lambda_4= -5.29869 . $$ Коэффициенты $ f_1(lambda) $ можно определить по схеме Хорнера: $$ begin &1 & 47.888430 & 797.2787648 & 5349.455513 & 12296.55068 \ hline -17.86326 & 1 & underbrace_<p_>& underbrace_<p_> &underbrace_<p_>& approx 0 \ end $$ Собственным вектором, принадлежащим $ lambda_ $, будет $$left[ -0.0256_, 0.21938_, -0.24187_, 1.044526 right]^<^> .$$ ♦

Теорема 21. Характеристический полином явно выражается через суммы Ньютона с помощью следующего представления:

$$ f(lambda)=fracleft| begin s_1 &1 & & & &\ s_2&s_1& 2 & &mathbb O & \ s_3&s_2&s_1&3& & \ vdots& & & ddots &ddots & \ s_n&s_& s_ & dots &s_1&n \ lambda^n&lambda^&lambda^& dots &lambda&1 end right|_ . $$

Биографические заметки о Леверье ☞ ЗДЕСЬ.

Видео:Матричный метод решения систем уравненийСкачать

Метод Крылова

Рассмотрим произвольный ненулевой столбец $ Y_0=left[ y_^,dots,y_^ right]^<^> in mathbb C^n $. Cоставим итерационную векторную последовательность $$ Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_=Acdot Y_ . $$

Теорема 22. Определитель

$$ det left[begin Y_0&Y_&dots&Y_&Y_\ 1& lambda&dots&lambda^&lambda^n end right]_ $$ совпадает — с точностью до постоянного множителя — с характеристическим полиномом матрицы $ A_ $. Здесь $ |_ $ означает конкатенацию.

Доказательство. Легко видеть, что $$ Y_K=A^KY_0 quad npu quad K in . $$ Если $$ f(lambda)=det(A-lambda E) =(-1)^n lambda^n+a_1 lambda^+a_2 lambda^+dots+a_n , $$ то по теореме Гамильтона-Кэли: $$ (-1)^n A^n+a_1A^+dots+a_nE=mathbb O_ . $$ Это равенство останется справедливым и после умножения его на произвольный вектор, в том числе на $ Y_ $: $$ (-1)^n A^ncdot Y_0+a_1A^ cdot Y_0 +dots+a_ncdot Y_0=mathbb O_ iff $$ $$ iff quad (-1)^n Y_n+a_1Y_ +dots+a_nY_0=mathbb O . $$ Последнее равенство представляет линейную систему относительно неизвестных коэффициентов характеристического полинома. Можно решать ее по формулам Крамера, но мы пойдем другим путем. Дополним эту систему тождеством $ f(lambda)=(-1)^n lambda^n+a_1 lambda^+a_2 lambda^+dots+a_n $. Рассмотрим получившуюся систему как линейную однородную относительно столбца $ left[ a_n,a_,dots,a_1,1right]^ $. Поскольку эта система имеет нетривиальное решение, то ее определитель должен равняться нулю: $$ 0=det left[begin Y_0&Y_&dots&Y_&(-1)^nY_\ 1& lambda&dots&lambda^&(-1)^nlambda^n-f(lambda) end right]= $$ (представляем последний столбец в виде суммы двух столбцов и используем свойство 5 определителя) $$ =det left[begin Y_0&Y_&dots&Y_&(-1)^nY_\ 1& lambda&dots&lambda^&(-1)^nlambda^n end right]-f(lambda) det left[begin Y_0&Y_&dots&Y_ end right] . $$ Таким образом, $$ f(lambda)=(-1)^n frac<det left[begin Y_0&Y_&dots&Y_&Y_\ 1& lambda&dots&lambda^&lambda^n end right]><det left[begin Y_0&Y_&dots&Y_ end right]> , $$ если только знаменатель в этой дроби не обратится в нуль. ♦

Пример. Найти характеристический полином матрицы примера Леверье

$$ A=left(begin -5.509882&1.870086&0.422908&0.008814 \ 0.287865&-11.811654&5.711900&0.058717 \ 0.049099&4.308033&-12.970687&0.229326 \ 0.006235&0.269851&1.397369&-17.596207 end right) . $$

Решение. Возьмем $ Y_0=left[ 1,0,0,0 right]^ $. Имеем $$ begin Y_1=A Y_0= & Y_2=AY_1= & Y_3=AY_2= & Y_4=AY_3= \ left(begin -5.509882\ 0.287865 \ 0.049099 \ 0.006235 end right), & left(begin 30.917951\ -4.705449 \ 0.334184 \ 0.002223 end right), & left(begin -179.012509\ 66.388293 \ -23.087280\ -0.649145 end right), & left(begin 1100.720101\ -967.597333\ 576.522644\ -4.040153 end right) . end $$ $$ det left[begin Y_0&Y_&Y_2& Y_& Y_\ 1& lambda&lambda^2 &lambda^&lambda^4 end right]= left| begin 1 & -5.509882 & 30.917951 & -179.012509 & 1100.720101 \ 0 & 0.287865 & -4.705449 & 66.388293 & -967.597333\ 0 & 0.049099 & 0.334184 & -23.087280 & 576.522644\ 0 & 0.006235 & 0.002223 & -0.649145 & -4.040153 \ 1 & lambda & lambda^2 & lambda^3 & lambda^4 end right|= $$ $$ =0.348621 lambda^4+16.694915lambda^3+277.948166lambda^2+1864.932835lambda+4286.836454 = $$ $$ =0.348621 left(lambda^4+47.888430lambda^3+797.27876_lambda^2+5349.4555_lambda+12296.550_ right) . $$ ♦

После нахождения характеристического полинома можно найти его корни каким-либо 10) методом. Пусть $ lambda_^ $ — одно из собственных чисел, и оно — простое; тогда для нахождения соответствующего собственного вектора можно воспользоваться тем же приемом, что был задействован в предыдущем ПУНКТЕ. Вычислим 11) частное от деления $ f(lambda_) $ на $ lambda-lambda_ $ $$ f_(lambda)= f(lambda)/(lambda-lambda_)=(-1)^n(lambda^ +p_1lambda^+dots+p_lambda+p_) . $$ Тогда любой ненулевой столбец матрицы $ f_(A)^ $ будет собственным вектором, принадлежащим $ lambda_^ $. Но тогда и произвольная комбинация столбцов этой матрицы тоже будет собственным вектором (если только не обратится в нулевой вектор). В частности, это относится и к комбинации, записываемой в матричном виде $$ (-1)^n f_(A) Y_0 = A^Y_0 +p_1A^Y_0+dots+p_Y_0=Y_+p_1Y_+dots+p_Y_0 . $$ А комбинируемые векторы уже посчитаны.

Теперь обсудим исключительные случаи. При неудачном выборе $ Y_ $ определитель $$ det left[begin Y_0&Y_&dots&Y_ end right] $$ может обратиться в нуль. Эта неприятность обязательно произойдет если, например, наш выбор пал на вектор $ Y_0 $, совпадающий с собственным вектором матрицы $ A_ $. Вероятность такого события — нулевая. В общем же случае, трудно ожидать, чтобы $ n_ $ почти произвольных столбцов $ Y_0,Y_,dots,Y_ $ оказались линейно зависимыми — если только сама матрица $ A_ $ не обладает «скрытым дефектом» — типа рассмотренного в следующем примере.

Пример. Найти характеристический полином матрицы

Решение. При любом выборе $ Y_0 $ векторы $ $ оказываются линейно зависимыми: $$ Y_0= left(begin 1\ 0\ 0 end right), Y_1= left(begin 2\ 1\ 1 end right), Y_2= left(begin 6\ 5\ 5 end right),dots ; Y_0= left(begin 1\ 1\ 1 end right), Y_1= left(begin 4\ 4\ 4 end right),dots $$ Объяснение этого феномена состоит в том, что для матрицы $ A_ $ ее аннулирующий полином имеет степень меньшую ее порядка: $$ A^2-5 A+4 E = mathbb O . $$ Домножение этого равенства на произвольный столбец $ Y_0 $ и доказывает линейную зависимость системы $ $. ♦

Такая ситуация возможна только в случае, когда характеристический полином матрицы $ A_ $ имеет кратные корни (в рассмотренном выше примере $ lambda_=1 $ являлся двойным корнем $ det (A-lambda_ E) $); она исключительно редко встречается на практике.

Видео:Матрица линейного оператора (01)Скачать

Поиск всех собственных чисел

Существуют методы нахождения спектра матрицы, не требующие предварительного построения характеристического полинома.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

QR-алгоритм

Этот алгоритм основан на QR-разложении матрицы $ A $.

Теорема 23. Спектр матрицы $ A $ совпадает со спектром матрицы $ P^ A P $ при произвольной ортогональной матрице $ P $.

Доказательство. $$ det (P^ A P-lambda E)=det (P^ A P- lambda P^ E P)=det P^ (A -lambda E ) P = det (A -lambda E ) P P^ = det (A -lambda E ) , . $$ ♦

Пусть QR-разложение матрицы $ A $ имеет вид $$ A=Q_1R_1 , , $$ где $ Q_1 $ — ортогональная, а $ R_1 $ — верхнетреугольная матрицы. Тогда матрица $$ A_2=R_1Q_1 $$ имеет тот же спектр, что и матрица $ A $. Действительно, поскольку $$ A_2=Q_1^ A Q_1 , $$ то сработает предыдущая теорема. Вычислим QR-разложение матрицы $ A_2 $ $$ A_2=Q_2R_2 $$ и переставим местами матрицы этого произведения: $$ A_3=R_2Q_2 , . $$ Матрица $$ A_3= Q_2^ A_2 Q_2=Q_2^ Q_1^ A Q_1 Q_2 $$ продолжаем иметь те же собственные числа, что и матрица $ A $. Утверждается, что бесконечная последовательность матриц $$ <A_j=R_Q_>_^ $$ как правило, сходится к матрице $ A_ $, которая будет верхнетреугольной.

Теорема 24 [4]. Если все собственные числа матрицы $ A $ различны по модулю, то матрица $ A_ $ является верхнетреугольной и на ее главной диагонали стоят собственные числа матрицы $ A $.

Пример. Найти все собственные числа матрицы $$ A=left(begin 2 & 3 &-1\ 7 & 3 & 3 \ -1 & -2 & 4 end right) , . $$

Решение. $$ A_1=Aapprox underbrace<left(begin 0.272165 & 0.759752 & 0.590511 \ 0.952579 & -0.299517 & -0.053683 \ -0.136083& -0.577119 & 0.805242 end right)>_ underbrace<left(begin 7.348469 & 3.946400 & 2.041241\ 0 & 2.534941 & -3.966781 \ 0 & 0 & 2.469409 end right)>_ $$ Теперь переставляем матрицы произведения местами и строим QR-разложение получившейся матрицы: $$ quad Rightarrow quad A_2 = R_1Q_1approx left(begin 5.481481 & 3.222957 & 5.771191 \ 2.954542 & 1.530046 & -3.3303021 \ -0.336044 & -1.425143 & 1.988472 end right)approx $$ $$ approxunderbrace<left(begin -0.878992 & 0.022595 & 0.476300\ 0.473781 & -0.154267 & -0.867026 \ 0.053886 & -0.987771 & 0.146304 end right)>_ underbrace<left(begin -6.236096& -3.634658 & -3.387848\ 0 & 1.244502 & -1.319999\ 0 & 0 & 5.927198 end right)>_ $$ Продолжим процесс: $$ quad Rightarrow quad A_3 = R_2Q_2approx left(begin 7.020952& 3.766220 & -0.314568\ -0.660752 & 1.111870 & -1.272137\ 0.319398 & -5.854713 & 0.867177 end right) approx $$ $$ approx underbrace<left(begin -0.994581 & -0.065879 & 0.080426 \ 0.093601 & -0.230749 & 0.968501 \ -0.045246 & 0.970780 & 0.235665 end right)>_ underbrace<left(begin -7.059205 & -3.376839 & 0.154554 \ 0 & -6.188319 & 1.156106 \ 0 & 0 & -1.053002 end right)>_ $$ Замечаем тенденцию убывания элементов матриц $ $, стоящих под главной диагональю. $$ Rightarrow dots Rightarrow A_ approx left(begin mathbf_ & 2.758769 & -2.160057\ -0.0467437 & mathbf_ & -5.341014\ 0.000018 &-0.005924 & mathbf_ end right) approx $$ $$ underbrace<left(begin -0.999972 & -0.007483 & 0.000007 \ 0.007483 & -0.999971 & 0.001339 \ -0.000003 & 0.001339 & 0.999999 end right)>_<Q_> underbrace<left(begin -6.246197 & -2.725694 & 2.120031\ 0 & -4.429817 & 5.354807 \ 0 & 0 & -1.662479 end right)>_<R_> , . $$ Матрица $ Q_j $ уже близка к диагональной (с элементами $ pm 1 $), верхнетреугольность матрицы $ A_j $ также заметна, но точность приближения еще не достаточна. $$ Rightarrow dots Rightarrow A_ approx left(begin mathbf_ & 2.805821 & -2.020513 \ -0.001776 & mathbf_ & -5.388407\ 0 & 0 & -mathbf end right) approx $$ Точность приближения минимильного собственного числа существенно выше точностей приближения остальных чисел. $$ Rightarrow dots Rightarrow A_ approx left(begin mathbf_ & 2.807524 & -2.015076\ -0.000073 & mathbf_ & -5.390442\ 0 & 0 & -mathbf end right) , . $$ ♦

К сожалению условие теоремы достаточно ограничительно: собственные числа вещественной матрицы $ A $ могут оказаться и мнимыми, но тогда они одинаковы по модулю.

Как это обстоятельство сказывается на структуре матрицы $ A_ $ и дальнейшее развитие метода ☞ ЗДЕСЬ

Видео:Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

Частичная проблема собственных чисел

Задача. Найти максимальное по модулю собственное число матрицы $ A_ $.

Предположение . Будем считать сначала, что максимальное по модулю собственное число матрицы единственно.

Излагаемый ниже метод поиска этого собственного числа называется методом степенны́х итераций 12) .

Рассмотрим произвольный ненулевой столбец $ Y_0=left[ y_^,dots,y_^ right]^<^> in mathbb C^n $. Cоставим такую же итерационную векторную последовательность, как и в методе Крылова $$ Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_=Acdot Y_,dots , $$ (только теперь, в отличие от метода Крылова, считаем ее неограниченно продолжающейся) и выделим последовательность первых элементов этих векторов: $$y_^,y_^,dots,y_^,dots $$

Теорема 25. Как правило, предел

$$ lim_frac<y_^><y_^> $$ существует и он равен максимальному по модулю собственному числу матрицы $ A_ $.

Доказательство. Перенумеруем собственные числа $ lambda_,dots,lambda_n $ матрицы $ A_ $ так, чтобы $ lambda_ $ обозначило максимальное по модулю: $$|lambda_1|= max_<jin > |lambda_j| , quad |lambda_1|>|lambda_j| quad npu quad jin . $$ Очевидно, $$ Y_=A^Kcdot Y_0 ; $$ отсюда следует, что любой элемент столбца $ Y_ $ может быть линейно выражен через $ lambda_^K,dots,lambda_n^K $. В частности, это справедливо и для первого элемента: $$ y_^=C_1lambda_1^K+C_2lambda_2^K+dots+C_nlambda_n^K . $$ В этом представлении $ _^n $ — будут константами из $ mathbb C_ $ в случае если все собственные числа являются простыми, и полиномами из $ mathbb C[K] $ в случае, если имеются кратные собственные числа. Действительно, в первом случае существует базис пространства $ mathbb C^n $, состоящий из собственных векторов матрицы $ A_ $: $$ A_j=lambda_j_j quad npu quad jin . $$ Вектор $ Y_0 $ можно разложить по этому базису: $$Y_0=alpha_1_1+dots+alpha_n_n .$$ Тогда последовательным домножением на матрицу $ A_ $ получаем : $$begin Y_1=AY_0&=& alpha_1 lambda_1_1+dots+alpha_nlambda_n_n, \ dots & & dots \ Y_K=A^KY_0&=& alpha_1 lambda_1^K_1+dots+alpha_nlambda_n^K_n end $$ откуда и следует доказываемое равенство.

Во втором случае — когда имеются кратные собственные числа матрицы $ A_ $ — придется применять «тяжелую артиллерию» в виде жордановой нормальной формы; см. теорему $ 5 $ ☞ ЗДЕСЬ. Для простоты рассуждений, будем в оставшейся части доказательства считать все собственные числа матрицы различными. Имеем тогда $$ lim_ frac<y_^><y_^>= lim_ frac <lambda_1^left[C_1+ C_2(lambda_2/lambda_1)^+dots+ C_n(lambda_n/lambda_1)^ right]> <lambda_1^left[C_1+C_2(lambda_2/lambda_1)^+dots+ C_n(lambda_n/lambda_1)^ right]> =lambda_1 $$ поскольку $$ lim_ left| frac right|^K = 0 quad npu quad jin . $$ Исключительным случаем является ситуация $ C_1=0 $, в этом случае утверждение теоремы может оказаться несправедливым 13) . ♦

Как правило, вектор

$$ left[1, lim_frac<y_^><y_^>,dots, lim_frac<y_^><y_^>right]^<^> $$ будет собственным, принадлежащим максимальному по модулю собственному числу матрицы $ A_ $.

Пример. Для матрицы

$$ A=left(begin 2 & 3 &-1\ 7 & 3 & 3 \ -1 & -2 & -4 end right) $$ найти максимальное по модулю собственное число и принадлежащий ему собственный вектор.

Решение. Возьмем в качестве стартового столбца $ Y_0=[1,0,0]^<^> $. Имеем: $$ Y_1=AY_0=left( begin 2 \ 7 \ -1 end right), Y_2=AY_1=left( begin 26 \ 32 \ -12 end right), Y_3=AY_2=left( begin 160 \ 242 \ -42 end right),dots, $$ $$ Y_=left( begin \ \ end right), Y_=AY_=left( begin \ \ end right) $$ Смотрим на отношения первых элементов векторов: $$ begin K & 1 & 2 & 3 & 4 & 5 & dots & 15 & dots & 19 \ hline y_^/y_^ & 2 & 13 & 6.153846 & 6.8 & 7.180147 & dots & 6.900726 & dots & mathbf_ end $$ Далее, в соответствии со следствием, собственный вектор, принадлежащий найденному числу $$ approx left[1, frac<y_^><y_^>,frac<y_^><y_^>right]^<^> approx left[1, 1.51070_, -0.368902 right]^<^> $$ ♦

Теперь обсудим исключительные случаи алгоритма.

1. Нарушение сходимости итерационного процесса за счет неудачного выбора стартового вектора. Если в качестве $ Y_ $ оказался случайно взят собственный вектор $ mathfrak X_ $ матрицы $ A_ $, принадлежащий произвольному ее собственному числу $ lambda_ $, то предел последовательности из теоремы будет равен именно этому числу; если при этом $ |lambda_ | ne max_ | lambda_j | $, то мы выйдем за пределы смысла выражения «как правило». Понятно, что вероятность настолько плохого выбора нулевая, но и выбор $ Y_0 $ вблизи $ mathfrak X_ $ также может существенно замедлить скорость сходимости. Поэтому если возникает ситуация медленной «стабилизации» значащих цифр в десятичном приближении собственного числа, попробуйте сменить начальный вектор.

2. Нарушение условия предположения , выдвинутого в начале пункта: максимальное по модулю собственное число неединственно.

Пример. Найти максимальное по модулю собственное число матрицы примера Леверье

$$ A=left(begin -5.509882&1.870086&0.422908&0.008814 \ 0.287865&-11.811654&5.711900&0.058717 \ 0.049099&4.308033&-12.970687&0.229326 \ 0.006235&0.269851&1.397369&-17.596207 end right) . $$

Решение. Для столбца $ Y_0=[1,0,0,0]^<^> $ имеем $$y_^/y_^=-17.8_ ,$$ т.е. на $ 100 $-й итерации получаем лишь $ 3_ $ истинные десятичные цифры в представлении собственного числа. При этом компонентами векторов $ Y_ $ являются числа порядка $ 10^ $. Если мы посмотрим на ответ примера Леверье, то увидим, что имеются два собственных числа матрицы, близких по модулю. ♦

К сожалению, вероятность того факта, что у случайно выбранной матрицы два ее собственных числа будут иметь одинаковый модуль становится ненулевой если эта матрица выбирается из множества вещественных матриц. Дело в том, что в этом случае ее характеристический полином будет иметь вещественные коэффициенты, а мнимые корни такого полинома всегда пáрные — для любого невещественного корня $ lambda_^ $ полинома, комплексно сопряженное к нему число $ overline<lambda_> $ также будет корнем. При этом $ |lambda_|= |overline<lambda_> | $.

Пример. Для матрицы

Предположение 2 . Пусть два максимальных по модулю собственных числа матрицы разнесены по величине, например $$ |lambda_1| > | lambda_2 | > | lambda_ j | quad npu j in . $$

Обобщение степенного метода основывается на использовании последовательностей из каких-то двух компонент векторов $ Y_=AY_K $, например, наряду с уже использованной выше последовательностью первых компонент $$y_^,y_^,dots,y_^,dots $$ возьмем еще и аналогичную для вторых: $$y_^,y_^,dots,y_^,dots $$

Теорема 26 [Эйткен]. При практически любом выборе стартового вектора $ Y_0 ne mathbb O $ для последовательности

Доказательство. Построим квадратное уравнение $$ p_0x^2+p_1x+p_2 = 0 $$ имеющее корнями $ lambda_1 $ и $ lambda_2 $. Если существует базис рпостранства $ mathbb C^n $ $$Y_0=alpha_1_1+alpha_2_2+dots+alpha_n_n .$$ Тогда последовательным домножением на матрицу $ A_ $ получаем : $$begin Y_K=& alpha_1 lambda_1^K_1 &+alpha_2 lambda_2^K_2+dots &+alpha_nlambda_n^K_n, \ Y_=& alpha_1 lambda_1^_1 &+alpha_2 lambda_2^_2+dots &+alpha_nlambda_n^_n,\ Y_=& alpha_1 lambda_1^_1 & +alpha_2 lambda_2^_2+dots &+alpha_nlambda_n^_n. end $$ Отбрасываем из правых частей равенств слагаемые порядков возрастания ниже, чем $ lambda_2^K, lambda_2^, lambda_2^ $ соответственно, домножаем получившиеся приближенные равенства $$begin Y_K & approx alpha_1 lambda_1^K_1 &+alpha_2 lambda_2^K_2, & color times p_2 \ Y_& approx alpha_1 lambda_1^_1 &+alpha_2 lambda_2^_2, & color times p_1\ Y_ & approx alpha_1 lambda_1^_1 & +alpha_2 lambda_2^_2, & color times p_0 end $$ и складываем: $$ p_2 Y_K + p_1Y_ + p_0 Y_ approx mathbb O , . $$ В получившемся векторном равенстве выбираем первые две компоненты: $$ left< begin p_2 y_1^ + p_1 y_1^ + p_0 y_1^ approx 0 , , \ p_2 y_2^ + p_1 y_2^ + p_0 y_2^ approx 0 , , end right. $$ которые и позволят определить приближенное значение набора $ p_0,p_1,p_2 $. С точностью до числового сомножителя, искомый полином можно представить в виде определителя $$ p_0x^2+p_1x+p_2 approx left|begin y_1^ & y_1^ & y_1^ \ y_2^ & y_2^ & y_2^ \ 1 & x & x^2 end right| , . $$ Формулы Виета завершат доказательство. ♦

При выполнении условия предположения 2 имеет место равенство

Пример. Для матрицы

$$ A=left(begin 2 & 3 &-1\ 7 & 3 & 3 \ -1 & -2 & 4 end right) $$ найти первые два по порядку убывания модулей собственных числа.

Видео:МАТРИЦЫ математика УМНОЖЕНИЕ МАТРИЦ и простейшие операции с матрицамиСкачать

Задачи

Видео:Как найти определитель матрицы 2х2, 3х3 и 4х4Скачать

Источники

[2]. Уилкинсон Дж.Х. Алгебраическая проблема собственных значений. М.Наука. 1970, с.93-94

[3]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ. 1960

[4]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Характеристический многочлен матрицы

Напомним, что характеристическим многочленом квадратной матрицы (n-го порядка) называется многочлен . Степень характеристического многочлена совпадает с порядком матрицы . Рассмотрим другие свойства характеристического многочлена.

1. Характеристический многочлен квадратной матрицы n-го по рядка может быть представлен в виде

где — корни характеристического многочлена (собственные значения матрицы ) кратности соответственно, причем и .

Действительно, указанное разложение (7.24) имеет любой многочлен степени (см. следствие основной теоремы алгебры). Старший коэффициент характеристического многочлена вычисляется, разлагая определитель .

2. Характеристический многочлен квадратной матрицы n-го по рядка может быть представлен в виде произведения инвариантных множителей характеристической матрицы

В самом деле, характеристическая матрица имеет нормальный диагональный вид (7.9): , так как . Наибольший общий делитель (старший коэффициент которого равен единице) единственного минора n-го порядка матрицы отличается от определителя только множителем , т.е. характеристический многочлен . Подставляя , получаем (7.25).

3. Характеристические многочлены подобных матриц совпадают.

В самом деле, пусть матрицы и подобны, т.е. существует такая матрица , что . Преобразуем характеристический многочлен матрицы по теореме 2.2 (об определителе произведения матриц) с учетом свойства 4 обратной матрицы:

что и требовалось показать.

4. Характеристический многочлен матрицы n-го порядка имеет вид

Минор k-го порядка , составленный из элементов матрицы, стоящих на пересечении одноименных строк и столбцов, называется главным минором. В формуле (7.26) коэффициент при равен сумме главных миноров k-го порядка, в частности, след матрицы — это сумма главных миноров 1-го порядка, определитель матрицы — это главный минор n-го порядка.

Поясним формулу (7.26). Пусть — i-й столбец матрицы , — i-й столбец единичной матрицы . В этих обозначениях запишем характеристический многочлен матрицы

Представим этот определитель в виде суммы определителей, используя его линейность по каждому столбцу. Получим

Разлагая определители, стоящие в фигурных скобках, по столбцам единичной матрицы, получаем главные миноры матрицы , например:

Таким образом, коэффициент при равен сумме главных миноров к -го порядка матрицы .

5. Подобные матрицы имеют: равные определители, равные следы, равные суммы главных миноров одного и того же порядка, совпадающие спектры.

В самом деле, подобные матрицы имеют равные характеристические многочлены (по свойству 3). У равных многочленов — одинаковые корни (т.е. спектры подобных матриц совпадают), а также равные соответствующие коэффициенты в (7.26), которые по свойству 4 выражаются через главные миноры матриц.

6. Определитель матрицы равен произведению ее собственных значений (с учетом их кратности).

Действительно, характеристический многочлен можно разложить на множители (см. следствие основной теоремы алгебры):

где — корни многочлена (быть может, совпадающие). Отсюда . С другой стороны, по определению получаем