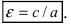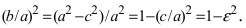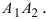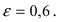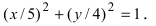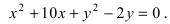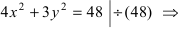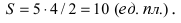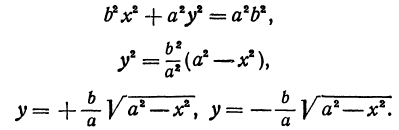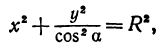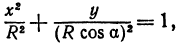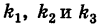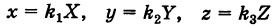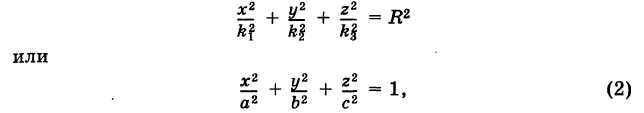Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 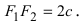
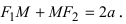
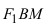
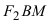
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 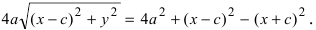
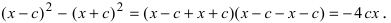
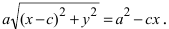
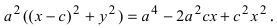
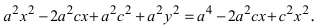
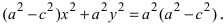
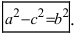
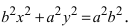
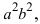
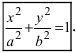
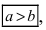
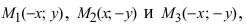
т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью ординат будут точки
(Рис. 30).
Определение: Найденные точки называются вершинами эллипса.
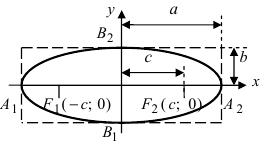
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 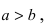
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 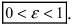
Если 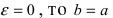
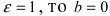
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 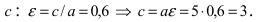
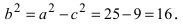
Пример:
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 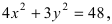
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
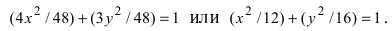
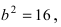
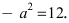
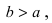
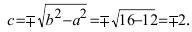
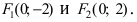
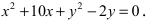
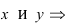
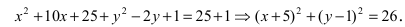
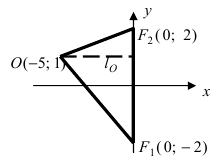
Построим в декартовой системе координат треугольник 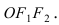
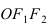
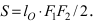
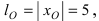
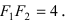
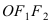
- Эллипс в высшей математике
- Уравнение эллипсоида
- Кривые второго порядка. Эллипс: формулы и задачи
- Понятие о кривых второго порядка
- Эллипс, заданный каноническим уравнением
- Решить задачи на эллипс самостоятельно, а затем посмотреть решение
- Продолжаем решать задачи на эллипс вместе
- Понятие эллипса в математике и его свойства
- Эллипс — что это такое, понятие в математике и геометрии
- Основные элементы и свойства фигуры
- Составление уравнения эллипса
- Как посчитать площадь всего эллипса и сегмента
- Формула для вычисления периметра и длины дуги
- Как построить эллипс по уравнению, примеры
- 🎬 Видео
Видео:3 Полуоси эллипсаСкачать

Эллипс в высшей математике
где 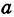
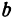
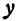
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
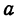

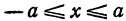
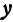
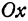
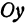
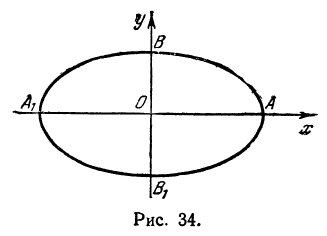
При 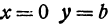
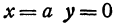
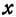

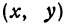
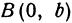
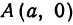
Полученная линия называется эллипсом. Число 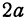
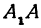
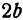
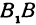
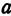
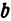
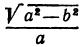
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
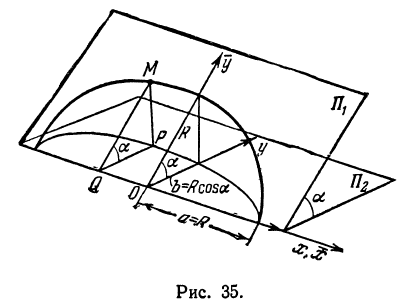
Возьмем две плоскости, пересекающиеся под углом 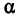
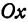
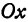
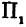
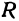
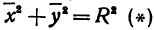
Пусть точка 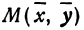
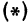
Обозначим проекцию точки 
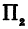
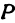
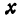
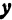


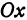
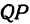
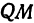
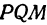
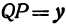
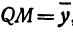
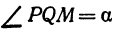
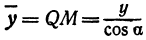


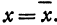
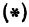
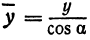
а это есть уравнение эллипса с полуосями 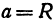
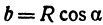
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Видео:ЭллипсСкачать

Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 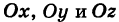
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 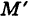
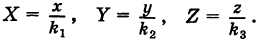
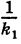
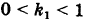
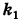
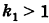
Подставляя эти формулы в уравнение (1), будем иметь
где 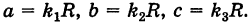
Величины 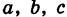
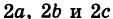
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Кривые второго порядка. Эллипс: формулы и задачи
Видео:найти уравнение касательной к эллипсуСкачать

Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:

где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Видео:§28 Эксцентриситет эллипсаСкачать

Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как 

Каноническое уравнение эллипса имеет вид:

где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка 

Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид 
Пример 1. Проверить, является ли линия, заданная общим уравнением 
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:

Точки 


называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет 
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением 
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

Получаем фокусы эллипса:
Видео:Эллипс (часть 8). Решение задач. Высшая математика.Скачать

Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет 
Видео:§18 Каноническое уравнение эллипсаСкачать

Продолжаем решать задачи на эллипс вместе
Если 



Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями

называются директрисами эллипса (на чертеже — красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса

где 



Пример 7. Дан эллипс 
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. 

Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки 

Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:

Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка 

Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:

Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.

так как из исходного уравнения эллипса 
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать

Понятие эллипса в математике и его свойства
Видео:11 класс, 52 урок, ЭллипсСкачать

Эллипс — что это такое, понятие в математике и геометрии
Эллипс — фигура, представляющая собой по форме замкнутую кривую линию на плоскости. Она получается путем пересечения плоскости с круговым цилиндром, или же как ортогональное отображение окружности на плоскость в пространстве.
В эллипсе суммарная величина расстояния от любой точки до двух точек F2 и F1 будет равна одному постоянному значению. Эти точки — F1 и F2 — носят названия фокусов эллипса.
F 1 M 1 + F 2 M 1 = F 1 M 2 + F 2 M 2 = A 1 A 2 = c o n s t
∣ F 1 M ∣ + ∣ F 2 M ∣ = 2 × a , причем ∣ F 1 F 2 ∣ 2 × a
Окружность можно называть партикулярным (особым) вариантом эллипса. Эллипс, как и параболу, и гиперболу, можно назвать квадрикой или же коническим сечением.
Рассмотрим связанные с эллипсом понятия:
- Отрезок AB, проходящий через фокусы эллипса (его концы должны лежать на эллипсе), носит название большой оси эллипса. Длина этого элемента — большой оси — равняется 2a в уравнении, приведенном выше.
- Малая ось эллипса — отрезок CD, который перпендикулярен большой оси, он проходит через центральную точку большой оси. Концы отрезка должны лежать на эллипсе.
- Центр эллипса — точка пересечения малой и большой оси данной замкнутой кривой.
- Большая полуось — отрезок, проведенный из центра эллипса к вершине большой оси. Обозначается буквой «a».
- Малая полуось — отрезок, проведенный из центра эллипса к вершине малой оси. Обозначается буквой «b».
- Фокальные радиусы в точке — расстояния r 1 и r 2 до определенной точки от каждого фокуса эллипса.
- Фокальное расстояние — расстояние, равное: c = ∣ F 1 F 2 ∣ 2 .
- Эксцентриситет — величина, равная: e = c a = 1 — b 2 a 2 .
- Диаметр эллипса — свободно проведенная хорда, проходящая через центр построения. Диаметры (обычно пара), обладающие свойством середины хорд, параллельные первому диаметру, и находящиеся на втором диаметре, называются сопряженными диаметрами. Середины хорд, параллельных второму диаметру, находятся на первом диаметре.
- Радиусом называют отрезок, соединяющий в данной точке центр эллипса и точку. Длина радиуса вычисляется по формуле: r = a b b 2 cos 2 γ + a 2 sin 2 γ = b 1 — e 2 cos 2 γ . В данной формуле γ — величина угла между большой полуосью и радиусом.
- Фокальный параметр ( p = b 2 a ) — половина длины хорды, проходящей через фокус эллипса, является перпендикулярной большой оси.
- Коэффициент сжатия, или же эллиптичность — отношение длины большой полуоси к длине малой полуоси. Вычисляется по формуле: k = b a . Величина, равная ( 1 — k ) = a — b a , будет носить название «сжатие эллипса». Следует помнить, что для окружности коэффициент сжатия равен единице, а сжатие равно нулю. Эксцентриситет и коэффициент сжатия связаны отношениями равными: k 2 = 1 — e 2 .
- Директриса — прямая, которая существует для каждого фокуса эллипса. При этом соотношение расстояния от свободно расположенной точки эллипса до фокуса этой замкнутой кривой к расстоянию от данной точки до определенной прямой будет равно эксцентриситету эллипса. Полный эллипс находится на той же стороне от такой же прямой, что и его фокус. Уравнения для директрис эллипса в классическом виде пишутся как x = ± p e ( 1 — e 2 ) для каждого фокуса ( ± p e 1 — e 2 , 0 ) . Расстояние от фокуса до директрисы будет вычисляться по соотношению p e
Теорема директрисы: Для того, чтобы определенная точка находилась на границе линии замкнутой кривой, необходимо, чтобы соотношение расстояния до фокуса к расстоянию до соответствующей директрисы было равно e.
Эллиптическая функция — функция в двух направлениях, которая в рамках метода комплексного анализа, задана на комплексной плоскости.
Видео:Разбор задания из теста по ангему | Уравнение эллипса | Уравнение касательной к эллипсуСкачать

Основные элементы и свойства фигуры
Рассмотрим элементы эллипса. Взгляните на чертеж:
F1 и F2 выступают в роли фокусов эллипса. Осями данной замкнутой кривой будут A1A2 =2a (как большая ось, проходящая сквозь фокусы замкнутой кривой), а B1B2=2b (как малая ось, перпендикулярная второй, большой оси фигуры, проходит через ее центр). Здесь «a» является большой полуосью, «b» является малой полуосью, «O» является центром (то есть точкой пересечения малой оси и большой оси).
Вершинами эллипса будут точки A1, и A2, и B1, и B2. Это точки пересечения большой осью и малой осью эллипса. Диаметр замкнутой кривой — отрезок, соединяющий две точки эллипса, а также проходящий через центр фигуры.
Фокальное расстояние, которое обозначается буквой «c», является половиной длины отрезка, соединяющего фокусы эллипса.
Эксцентриситет замкнутой кривой, который обозначается буквой «e», показывает степень «сплющенности» (то есть отклонения от окружности). Он определяется соотношением фокального расстояние (буква «c») к большой полуоси «a». В случае эллипса эксцентриситет будет таким: 0 1.
Фокальные радиусы в точке — расстояния r 1 и r 2 до определенной точки от каждого фокуса эллипса.
Радиус эллипса — отрезок, соединяющий центр, который обозначается буквой «O» с точкой на самом эллипсе.
r = a b b 2 cos 2 γ + a 2 sin 2 γ = b 1 — e 2 cos 2 γ .
В данной формуле γ — величина угла между большой полуосью и радиусом (A1A2), e — эксцентриситет.
Фокальный параметр — отрезок, перпендикулярный большой полуоси, а также выходящий за фокус эллипса. Вычисляется по формуле: p = b 2 a
Коэффициент сжатия или же эллиптичность, обозначаемая буквой «k», является отношением длины малой полуоси к большой полуоси.
Малая полуось всегда будет меньше, чем большая полуось замкнутой кривой. Получается, что k k = b a
В данном уравнении величина «e» — эксцентриситет.
Сжатие эллипса (то есть 1 — k ) — показатель, который равен разности между эллиптичностью и единицей.
Директриса эллипса — пара прямых, которые перпендикулярны фокальной оси замкнутой прямой, пересекающей расстояние a*e от центра замкнутой прямой. Расстояние до директрисы от фокуса будет равно p*e.
Рассмотрим также основные свойства эллипса:
- Угол к эллипсу между касательной и фокальным радиусом r 1 будет равен величине угла между фокальным радиусом r 2 и касательной.
- Равенство касательной к замкнутой кривой в точке M : 1 = x x M a 2 + y y M b 2
- В случае, если замкнутая прямая пересекается парой параллельных прямых, то отрезок, соединяющий середины отрезков, образованных при пересечении эллипса и прямых, всегда будет пересекать центр замкнутой кривой.
Примечание 2
Данное свойство позволяет построить центр эллипса при помощи циркуля и линейки.
- Эволюта замкнутой кривой — астероида, которая растянута по короткой оси.
- В случае, если можно вписать эллипс с фокусами F1 и F2 в треугольник ABC, то возможно выполнить данное соотношение:
1 = F 1 A × F 2 C A × A B + F 1 B × F 2 B A B × B C + F 1 C × F 1 C B C × C A
Видео:Видеоурок "Эллипс"Скачать

Составление уравнения эллипса
Базовое уравнение замкнутой кривой.
Это уравнение, описывающее эллипс в декартовой системе координат. В случае, если центр замкнутой кривой (обозначается буквой «O») — в начале системы координат, а на абсциссе находится большая ось, то замкнутая кривая будет описываться следующим уравнением:
1 = x 2 a 2 + x 2 b 2
В случае, если центр эллипса смещается в точку с координатами x 0 и y 0 , то уравнение примет следующий вид:
1 = ( x — x 0 ) 2 a 2 + ( y — y 0 ) 2 b 2
Параметрическое уравнение будет выглядеть следующим образом:
Видео:166. Найти каноническое уравнение эллипса.Скачать

Как посчитать площадь всего эллипса и сегмента
Рассмотрим формулу для вычисления площади всего эллипса:
Рассмотрим формулу для вычисления площади сегмента эллипса. Это формула площади сегмента, который лежит на левой стороны от хорды с координатами (x, y), а также (x, -y).
S = π a b 2 — b a ( x a 2 — x 2 + a 2 × arcsin x a )
Видео:Определить тип кривой (эллипс)Скачать

Формула для вычисления периметра и длины дуги
Рассмотрим формулу для вычисления периметра замкнутой кривой.
Важно запомнить, что точную формулу для периметра L найти крайне тяжело. Ниже приведена формула, с помощью которой можно приблизительно рассчитать длину периметра. Максимальной погрешностью данной формулы можно считать примерно 0,63 %.
L ≈ 4 π a b + ( a — b ) 2 a + b
Рассмотрим формулу для вычисления длины дуги замкнутой кривой:
- Параметрическое уравнение для вычисления длины дуги замкнутой кривой через большую полуось a, а также малую полуось b:
Формула 8
ℓ = ∫ t 1 t 2 a 2 sin 2 t + b 2 cos 2 t d t .
- Параметрическое уравнение для вычисления длины дуги замкнутой кривой с помощью большой полуоси a, а также эксцентриситета, который обозначается буквой e:
Формула 9
ℓ = ∫ t 1 t 2 1 — e 2 cos 2 t d t , e 1 .
Видео:Найти все касательные к эллипсу проходящие через начало координатСкачать

Как построить эллипс по уравнению, примеры
Попробуем построить эллипс по уравнению x 2 16 + y 2 7 = 1
Сначала мы должны привести данное уравнение к привычному виду: x 2 4 2 + y 2 ( 7 ) 2 = 1
Определяем вершины эллипса. Они находятся в точках A1(a; 0), A2 (-a; 0), B1 (0; b), B2 (0; -b). Получаем, что A 1 ( 4 ; 0 ) , A 2 ( — 4 ; 0 ) , B 1 ( 0 ; 7 ) , B 2 ( 0 ; — 7 )
🎬 Видео
Фокусы эллипсаСкачать

§20 Построение эллипсаСкачать
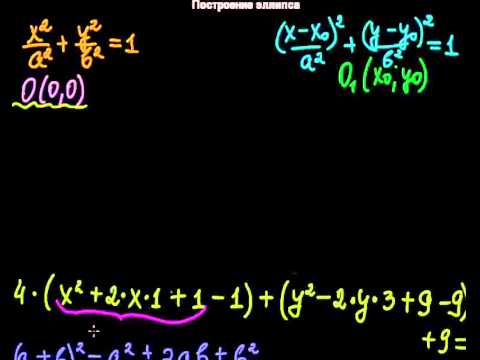
Эллипс (часть 1). Каноническое уравнение. Высшая математика.Скачать

§17 Определение эллипсаСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

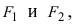
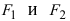
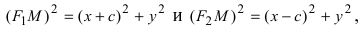
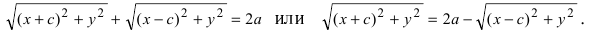
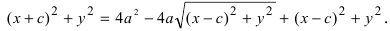
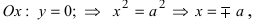 т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью абсцисс будут точки 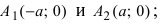
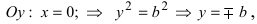 т.е. точками пересечения эллипса с осью ординат будут точки
т.е. точками пересечения эллипса с осью ординат будут точки 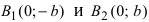 (Рис. 30).
(Рис. 30).