Как найти критические точки функции по уравнению (3 видео)

Экстремумы функции

Содержание

Необходимое условие экстремума функции одной переменной
Достаточное условие экстремума функции одной переменной
Как найти критические точки функции по уравнению
Контакты
Построение графиков функций
Понятие функции
Понятие графика функции
Исследование функции
Построение графика функции
🎥 Видео

Видео:Найти точки экстремума функцииСкачать

Необходимое условие экстремума функции одной переменной

Видео:Критические точки функцииСкачать

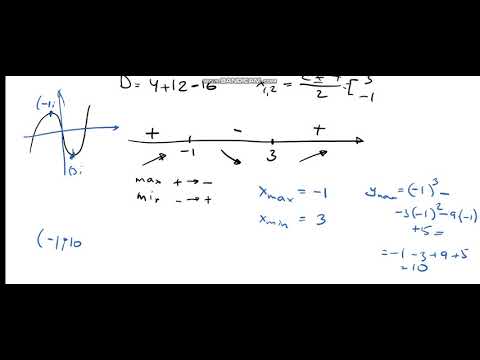
Достаточное условие экстремума функции одной переменной

Если в точке x * выполняется условие:

Пример №1 . Найти наибольшее и наименьшее значения функции: на отрезке [1; 3].
Решение.

Критическая точка одна x₁ = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 /₂, f(3)=3 8 /₈₁
Ответ: f_min= 5 /₂ при x=2; f_max=9 при x=1

Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π /₃+2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x= π /₃+2πk, k∈Z – точки минимума функции; , значит x=- π /₃+2πk, k∈Z – точки максимума функции.

Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x₀ или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.

Пример №4 . Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x — x 2

Видео:АЛГЕБРА С НУЛЯ — Точки Экстремума ФункцииСкачать

Как найти критические точки функции по уравнению

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Видео:Критические точки функцииСкачать

Построение графиков функций

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Производная. Часть 10. Экстремумы. Максимум и минимум. Стационарная и критическая. Перегиба и полюс.Скачать

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ — наглядно.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Видео:Критические точкиСкачать

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Видео:Алгебра 10 Критические точкиСкачать

Исследование функции

Важные точки графика функции y = f(x):

стационарные и критические точки;
точки экстремума;
нули функции;
точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

Найти область определения функции.
Найти область допустимых значений функции.
Проверить не является ли функция четной или нечетной.
Проверить не является ли функция периодической.
Найти нули функции.
Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
Найти асимптоты графика функции.
Найти производную функции.
Найти критические точки в промежутках возрастания и убывания функции.
На основании проведенного исследования построить график функции.

Как найти критические точки функции по уравнению

У нас есть отличные курсы по математике для учеников с 1 по 11 классы!

Видео:Стационарные и критические точки функции на графике функции, по формуле функции. Алгебра 10 классСкачать

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

x	y
0	-1
1	2

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

x	y
0	2
1	1

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

x	y
0	0
1	2

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Преобразование в одно действие типа f(x — a).

Сдвигаем график вправо на 1:

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.