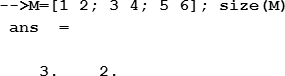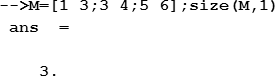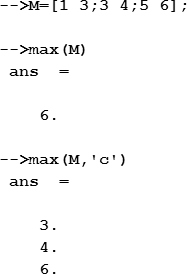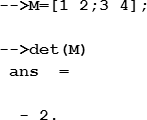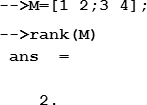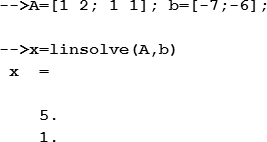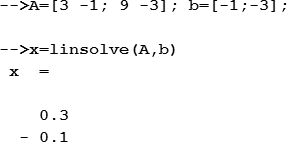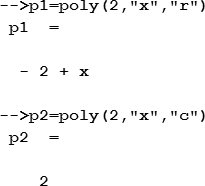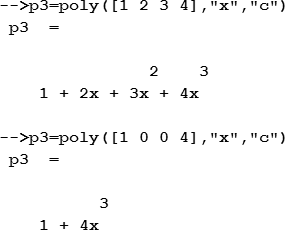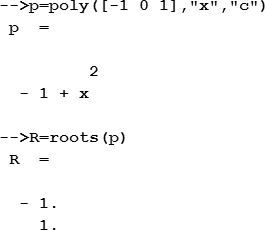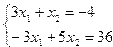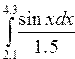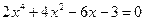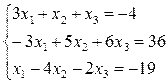Решение задач линейной алгебры
Функции для нахождения числовых характеристик матриц
Для определения количества строк и столбцов матрицы М используют функцию size, аргументом которой является имя массива:
Если нужно определить количество только строк или только столбцов, то синтаксис функции модифицируется: добавляется второй аргумент, который имеет значение «1» или «r», если следует определить количество строк, «2» или «с» — если столбцов. Например:
Общее количество элементов матрицы или длину вектора вычисляет функция length, аргументом которой является имя матрицы или вектора:
Для определения максимального значения элемента матрицы или вектора используется функция max, аргументом которой является имя матрицы или вектора. Если нужно определить максимальное значение для каждого из строк или столбцов матрицы, то синтаксис функции модифицируется: добавляется второй аргумент, который имеет значение «r», если следует определить максимальное значение для каждой строки, или «c» — если для каждого столбца:
Аналогично используется функция min, предназначенная для определения минимального значения элемента матрицы или вектора.
Для вычисления определителя (детерминанта) квадратной матрицы используется функция det, аргументом которой является имя матрицы:
Для вычисления ранга матрицы используется функция rank, аргументом которой является имя матрицы:
Функции, реализующие численные алгоритмы решения задач линейной алгебры
Вычисление матрицы, обратной М
Напомним, что обратной по отношению к матрице М называется такая матрица, которая при ее умножении на матрицу М дает единичную матрицу.
Как видим, обратная матрица А достаточно близка к единичной, но все же полностью ею не является, что является следствием погрешности численных вычислений.
Scilab позволяет решать системы линейных алгебраических уравнений вида Ax=b. В документе для значений A формируется матрица коэффициентов при неизвестных, каждая строка которой содержит коэффициенты одного уравнения, а для значений b формируется вектор-столбец из свободных коэффициентов.
После этого для решения системы используется функция linsolve, имеющая такой синтаксис:
где A — это матрица коэффициентов при неизвестных, b — вектор-столбец свободных коэффициентов.
Функция возвращает найденные значения неизвестных системы в виде вектора.
Таким образом, решение системы линейных уравнений 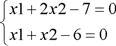
Искомые значения: х1=5, х2=1.
Если система не имеет решения, то об этом выдается сообщение «WARNING: Conflicting linear constraints!» (Конфликтующие условия для линейных уравнений). Например, такая ситуация возникнет при попытке решения системы линейных уравнений 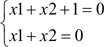
Система линейных алгебраических уравнений может иметь множество решений. В таком случае функция возвращает только одно. Ниже приведен пример такой ситуации при решении системы линейных уравнений 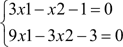
Работа с полиномами
Напомним, что полиномом или алгебраическим уравнением называется уравнение вида a0x n + a1x n-1 + . + an-1x + an.
Для создания полинома используется функция poly.
где р — это имя полинома (его можно и не задавать).
Аргументы функции: a — матрица или вещественное число, x — символьная переменная, «flag» — символьная переменная, которая определяет способ задания полинома и имеет значение «roots» (допускается сокращение «r») или «coeff» («c»). По умолчанию — «roots». Если «roots» имеет значение «r», то полином создается с параметрами ai для соответствующих символьных переменных xi. Если «flag» имеет значение «c», то значения параметров ai воспринимаются как корни, для которых нужно рассчитать коэффициенты полинома.
Следующий пример демонстрирует использование функции poly для создания полиномов р1, который имеет корень «2» и р2 с коэффициентом «2»:
В следующих примерах создаются полиномы с соответствующими коэффициентами для кубического уравнения.
С полиномами можно производить действия умножения, создавать из них дроби (деление), складывать и вычитать.
Решение уравнения с одним неизвестным
Scilab может решать алгебраическое уравнение с одним неизвестным. Например, нужно найти корни уравнения x 2 = 1. Если — как в данном примере — уравнение не имеет вида полинома, то его следует предварительно преобразовать в полином: x 2 — 1 = 0. После этого используется функция roots, единственным аргументом которой является имя полинома. Функция возвращает найденные корни полинома.
Если уравнение не имеет решения на множестве вещественных чисел (x 2 + 1 = 0), то Scilab ищет решение среди комплексных чисел:
Вычисление сумм элементов матрицы
Для вычисления суммы значений элементов матрицы используется функция sum.
Если следует вычислить отдельно сумму значений для каждого столбца, то вторым аргументом функции является число «1» или буква «с», а если для строки, то — «2» или буква «r».
Вычисление произведения элементов матрицы
Для вычисления произведения используется функция prod.
Если следует вычислить отдельно произведение значений каждого столбца, то вторым аргументом функции является число «1» или буква «с», а если для строки, то — «2» или буква «r».
Дифференциалы
Для нахождения дифференциалов в определенной точке используется функция numdiff, первый аргумент которой является именем функции, которую нужно продифференцировать, а второй — координата точки, в которой нужно вычислить производную.
Видео:Решение систем линейных уравнений в Scilab.aviСкачать

Как найти корни уравнения в scilab
—>p2^(-1) //Возведение в отрицательную степень
Функция roots ( p ) предназначена для решения алгебраического уравнения.
Здесь p — это полином, созданный функцией poly и представляющий собой левую часть уравнения P(x) = 0.
Решим несколько алгебраических уравнений.
Задача 7.1 . Найти корни полинома 2x 4 − 8x 3 + 8x 2 − 1 = 0.
Для решения этой задачи необходимо задать полином p . Сделаем это при помощи функции poly, предварительно определив вектор коэффициентов V . В уравнении отсутствует переменная x в первой степени, это означает, что соответствующий коэффициент равен нулю:
Листинг 7.4 . Формирование полинома
1 + 8x 2 — 8x 3 + 2x 4
Теперь найдем корни полинома:
Листинг 7.5. Использование функции roots
Графическое решение задачи позволяет убедиться, что корни найдены верно.
Пересечение графиков функций F( x )= 1 + 8x 2 — 8x 3 + 2x 4 и g ( x )=0
Задача 7.2. Найти корни полинома x 3 + 0.4x 2 + 0.6x − 1 = 0.
Листинг 7.6. Решение задачи 7.2
Нетрудно заметить, что полином имеет один действительный и два комплексных корня.
Задача 7.3. Найти решение уравнения y(x) = 0, если y(x) = x 4 − 18x 2 + 6.
Листинг 7.7. Решение задачи 7.3
Приведите графическое решение данного уравнения.
Уравнение f(x) = 0, в котором неизвестное входит в аргумент трансцендентных функций, называется трансцендентным уравнением .
К трансцендентным уравнениям принадлежат показательные, логарифмические и тригонометрические.
В общем случае аналитическое решение уравнения f(x) = 0 можно найти только для узкого класса функций. Чаще всего приходится решать это уравнение численными методами.
Численное решение нелинейного уравнения проводят в два этапа.
- В начале отделяют корни уравнения, т.е. находят достаточно тесные промежутки, в которых содержится только один корень. Эти промежутки называют интервалами изоляции корня , определить их можно, изобразив график функции f(x) или любым другим методом.
- На втором этапе проводят уточнение отделенных корней, или, иначе говоря, находят корни с заданной точностью.
Для решения трансцендентных уравнений в Scilab применяют функцию
где x0 — начальное приближение, f — функция, описывающая левую часть уравнения y(x) = 0.
Рассмотрим применение этой функции на примерах.
Задача 7.4. Найти решение уравнения
Определим интервал изоляции корня заданного уравнения. Воспользуемся графическим методом отделения корней. Если выражение, стоящее в правой части уравнения, представить в виде разности двух функций f (x) − g(x) = 0 , то абсцисса точки пересечения линий f(x) и g(x) — корень данного уравнения. В нашем случае .
Корень данного уравнения лежит в интервале [0; 1].
Выберем ноль в качестве начального приближения, зададим функцию, описывающую уравнение и решим его:
Листинг 7.8. Решение задачи 7.4
Задача 7.5. Найти корни уравнения f(x) = e x /5 − 2(x − 1) 2 .
На рисунке видно, что график функции f(x) трижды пересекает ось абсцисс, т.е. уравнение имеет три корня.
Последовательно вызывая функцию fsolve с различными начальными приближениями, получим все решения заданного уравнения:
Листинг 7.9. Решение задачи 7.5
Кроме того, начальные приближения можно задать в виде вектора, и тогда функцию можно вызвать один раз:
Листинг 7.10. Решение задачи 7.5 (альтернативный способ)
Задача 7.6. Вычислить корни уравнения sin(x) − 0.4x = 0 в диапазоне [−5π; 5π].
Решение задачи представлено в листинге 7.11.
Листинг 7.11 . Решение задачи 7.6
—>X //Множество решений
X = !-16.11948 -12.154854 -9.8362948 -5.8716685 -3.5531095
0.4115168 2.7300758 6.6947022 9.0132611 12.977887 15.296446!
Задача 7.7. Найти решение уравнения y(x) = 0, если y(x) = x 5 − x 3 + 1.
Видео:Решение трансцендентных уравнений в Scilab.aviСкачать

Вычисление интегралов, решение уравнений и систем
Краткие теоретические сведения
В Scilab вычисление определенного интеграла методом трапеций реализовано функцией
где x –вектор значений аргумента подынтегральной функции на отрезке интегрирования, y –вектор значений, полученных при вычислении подынтегральной функции для элементов вектора x.
Например, для вычисления 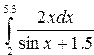
| Фрагмент программы x=2:0.01:5.3 y =2*x./(sin(x)+1.5) integral = inttrap(x,y)disp(integral) | Результат 30.436962 |
Для вычисления определенного интеграла с использованием алгоритма квадратурных формул предназначена функция
Integrate(fun, x, a, b, ,er1 ,er2),
где fun– подынтегральная функция в символьном виде, x – переменная интегрирования в символьном виде, a, b –пределы интегрирования, er1,er2 –абсолютная и относительная погрешности интегрирования (необязательные параметры).
Например, для вычисления 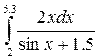
| Фрагмент программы z=integrate(‘2*x./(sin(x)+1.5)’, ‘x’, 2, 5.3)disp(z) | Результат 30.437056 |
Универсальная команда интегрирования:
[integral,err]=intg(a, b, name ,er1,er2),
где a, b –пределы интегрирования, name – имя подынтегральной функции (может быть задана с помощью внешней функции), er1,er2 –абсолютная и относительная погрешности интегрирования (необязательные параметры). Функция intgвозвращает значение интеграла (integral) и погрешность вычислений (err).
Внешнюю функцию можно задать командой
deff(‘переменная=имя функции(параметр)’, ‘символьное представление функции’) Например, deff(‘y=F(x)’, ‘y=2*x./(sin(x)+1.5)’).или
function переменная = имя функции(параметр-аргумент функции)
операторы, вычисляющие значение функции
endfunctionНапример, function y=f(t) y=t^2/sqrt(3+sin(t)) endfunctionилиfunction y=f(t),y=t^2/sqrt(3+sin(t)),endfunction
Ниже приводится пример вычисления интеграла 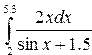
| Фрагмент программы function y=f(x) y=2*x./(sin(x)+1.5)endfunctionz=intg(2,5.3,f), disp(z) | Результат 30.437056 |
Для решения нелинейных уравнений в Scilab используется функция
где x0 –начальное приближение корня, f– функция, описывающая левую часть уравнения f(x)=0.
Например, для решения уравнения 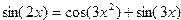
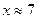
| Фрагмент программы deff(‘y=F(x)’, ‘y=sin(2*x)-cos(3*x.^2)-sin(3*x)’)root=fsolve(7,F)disp(root) | Результат 6.9755674 |
Для решения полиномиальных уравнений вида 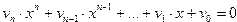
где а – вектор коэффициентов перед неизвестными полинома размерностью n+1(n – порядок полинома).
Результатом работы этой функции будет вектор корней полинома размерностью n.
Пример решения полиномиального уравнения 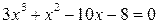
| Фрагмент программы v=[3 1 -10 -8]R=roots(v)disp(R) | Результат 2. -1.3333333 — 1. |
Для уравнения 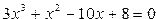
| Фрагмент программы v=[3 1 -10 8]R=roots(v)disp(R) | Результат — 2.2935835 0.9801251 + 0.4494650i 0.9801251 — 0.4494650i |
Функция rootsможет также принимать в качестве параметра полином, созданный функциейpolyи представляющий собой левую часть уравнения 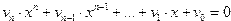
где a –вектор коэффициентов полинома записанных в обратном порядке, x — символьная переменная, f1– символьная переменная, принимающая значения ‘c’ или ‘r’ (roots или coeff).
Например, чтобы создать полином 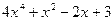
| Фрагмент программы p=poly([3 -2 1 0 4],’x’,’c’)disp(p) | Результат 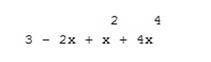 |
Для решения уравнения 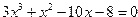
| Фрагмент программы p=poly([-8 -10 1 3],’x’,’c’)R=roots(p)disp(R) | Результат 2. — 1.3333333 — 1. |
Для решения систем линейных уравнений в Scilab есть следующие способы:
— применение операции левого матричного деления;
— использование обратной матрицы.
Если задана система линейных алгебраических уравнений вида:
где А – матрица коэффициентов перед неизвестными системы, В – вектор свободных членов, то решение системы может быть найдено в виде:
То же самое решение может быть получено с помощью обратной матрицы, например:
Например, решить систему уравнений
| Фрагмент программы A=[3 1;-3 5]; B=[-4 ;36]; X=inv(A)*B, disp(X)илиX1=AB , disp(X1) | Результат — 3.1111111 5.3333333 |
Для решения систем нелинейных уравнений можно использовать функцию
где x0 –вектор начальных приближений для неизвестных, f –функция, определяющая систему
Например, решение системы 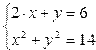
| Фрагмент программы function [y]=fun(x) y(1)=2*x(1)+x(2)-6 y(2)=x(1)^2+x(2)^2-14endfunctionX0=[1;1]R=fsolve(X0,fun)disp(R) | Результат 1.2338096 3.5323808 |
Задание 1. Вычисление определенного интеграла
Постановка задачи. Вычислить числовое значение интеграла от этой функции в заданных пределах интегрирования методом трапеций, методом квадратурных формул и с помощью функции intg.
Шаг 1. Создадим вектор X, значения которого будут изменяться от 2,1 до 4,3 с шагом 0.01.
Шаг 2. Создадим вектор Y, каждое значение которого вычисляется по формуле 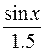
Шаг 3. Применим команду inttrap(X, Y).
Шаг 4. Используем функцию integrate,задав подынтегральную функцию в символьном виде.
Шаг 5. Определим внешнюю функцию с помощью команды deffили конструкции function
Шаг 6. Выведем результаты, используя команду disp.
| Программа | Результат выполнения |
| X =2.1:0.01:4.3 Y =sin(X)/1.5 integral_1 = inttrap(X,Y)integral_2=integrate(‘sin(x)/1.5’, ‘x’, 2.1, 4.3)disp(integral_1)disp(integral_2) | — 0.0693640 — 0.0693646 |
| deff(‘y=F(x)’,’y=sin(x)/1.5′); integral_3=intg(2.1,4.3,F)function y=f(x) y=sin(x)/1.5endfunctionintegral_4=intg(2.1,4.3,f)disp(integral_3)disp(integral_4) | — 0.0693646 — 0.0693646 |
Индивидуальные задания приведены в таблице 3.4.
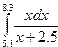 | 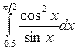 | 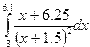 |
 | 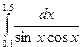 | 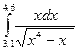 |
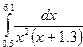 | 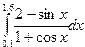 | 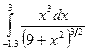 |
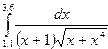 | 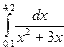 | 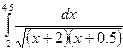 |
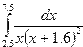 | 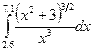 | 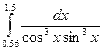 |
Задание 2. Поиск корней уравнения, графическая интерпретация
Постановка задачи. Найти корень уравнения для заданного начального приближения. Выполнить графическую интерпретацию результата.
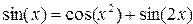 |  |
Шаг 1. Определим внешнюю функцию с помощью команды deffили конструкции function
Шаг 2. Найдем корень уравнения с помощью функции fsolve,подставив в качестве первого параметра заданное начальное приближение.
Шаг 3. Выведем результат, используя команду disp.
Шаг 4. Выполним графическую интерпретацию результата. Для этого зададим аргумент функции из левой части уравнения таким образом, чтобы найденный корень попадал в диапазон между первым и последним элементом вектора. Построим график функции из левой части уравнения с помощью plot.Построим также линию y=0 и отметим точку с абсциссой, равной корню, и ординатой, равной значению функции для корня.
| Программа | Результат выполнения |
| deff(‘y=F(x)’, …’y=sin(x)-cos(x.^2)-sin(2*x)’)root=fsolve(1,F)disp(root)x=0.5:0.01:2.5plot(x,F(x),’-b’,root,F(root),’xr’,x,0,’-k’) | 1.1695683 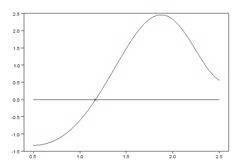 |
Индивидуальные задания приведены в таблице 3.5
| Вариант | Уравнение | Начальноеприближение |
| 1. | 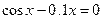 | 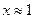 |
| 2. | 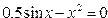 | 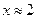 |
| 3. | 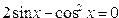 | 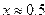 |
| 4. | 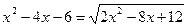 | 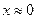 |
| 5. | 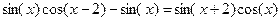 | 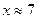 |
| 6. | 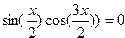 |  |
| 7. | 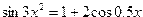 | 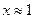 |
| 8. | 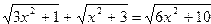 | 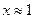 |
| 9. | 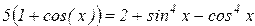 | 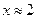 |
| 10. | 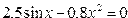 | 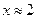 |
| 11. | 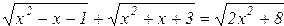 | 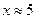 |
| 12. | 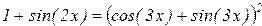 | 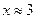 |
| 13. | 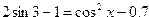 | 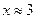 |
| 14. |  | 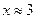 |
| 15. | 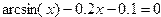 | 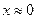 |
Задание 3. Поиск корней полиномиального уравнения, графическая интерпретация
Постановка задачи. Найти все корни полиномиального уравнения. Выполнить графическую интерпретацию для одного из найденных действительных корней.
Шаг 1. Создадим вектор коэффициентов полинома в левой части уравнения (или полином с помощью poly)
Шаг 2. Найдем корни уравнения с помощью функции roots.
Шаг 3. Выведем результат, используя команду disp.
Шаг 4. Выполним графическую интерпретацию результата. Для этого зададим аргумент функции из левой части уравнения таким образом, чтобы выбранный действительный корень попадал в диапазон между первым и последним элементом вектора. Построим график функции из левой части уравнения с помощью plot.Построим также линию y=0 и отметим точку с абсциссой, равной корню, и ординатой, равной значению функции для корня.
| Программа | Результат выполнения |
| v=[2 0 4 -6 -3]R=roots(v)disp(R)root=R(3)x=0.5:0.01:2y=2*x.^4+4*x.^2-6*x-3F_root=2*root^4+4*root^2-6*root-3plot(x,y,’-b’,root,F_root,’xr’,x,0,’-k’) | — 0.4129576 + 1.7282075i — 0.4129576 — 1.7282075i 1.2164706 — 0.3905555 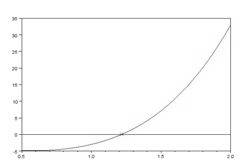 |
Индивидуальные задания приведены в таблице 3.6.
| Вариант | Уравнение |
| 1. | 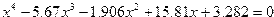 |
| 2. |  |
| 3. | 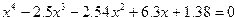 |
| 4. | 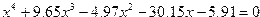 |
| 5. | 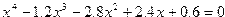 |
| 6. | 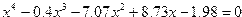 |
| 7. | 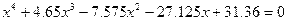 |
| 8. | 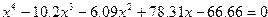 |
| 9. | 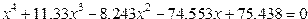 |
| 10. | 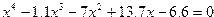 |
| 11. | 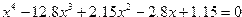 |
| 12. | 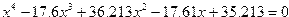 |
| 13. | 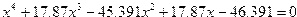 |
| 14. |  |
| 15. | 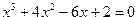 |
Задание 4. Решение системы линейных уравнений
Постановка задачи. Решить систему линейных уравнений.
Шаг 1. Создадим матрицу коэффициентов при неизвестных
Шаг 2. Создадим вектор свободных членов.
Шаг 3. Умножим матрицу, обратную к матрице коэффициентов, на вектор свободных членов (или применим операцию левого матричного деления).
Шаг 4. Выведем результат, используя команду disp.
| Программа | Результат выполнения |
| A=[3 1 1;-3 5 6;1 -4 -2]; B=[-4 ;36;-19]; X=inv(A)*B disp(X) | — 3. 3. 2. |
Индивидуальные задания приведены в таблице 3.7.
| № | Система уравнений | № | Система уравнений |
| 1. | 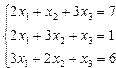 | 2. | 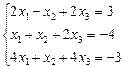 |
| 3. | 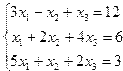 | 4. | 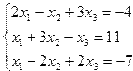 |
| 5. | 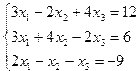 | 6. | 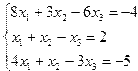 |
| 7. | 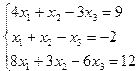 | 8. | 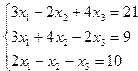 |
| 9. | 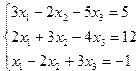 | 10. | 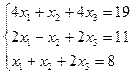 |
| 11. | 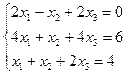 | 12. | 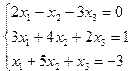 |
| 13. | 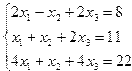 | 14. | 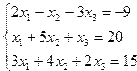 |
| 15. | 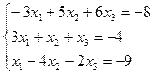 | 16. | 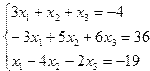 |
Статьи к прочтению:
Метод Крамера за 3 минуты. Решение системы линейных уравнений — bezbotvy
Похожие статьи:
Приближенное вычисление интегралов Приближённое вычисление определённого интеграла основано на геометрическом смысле интеграла и сводится к приближённому…
Задание: графически и численно решить систему нелинейных алгебраических уравнений, на примере поиска точек пересечения двух функций. Исходные данные:…
💡 Видео
Решение уравнений в ScilabСкачать

Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать

Scilab 2. ODEСкачать

Решение ДУ в ScilabСкачать

Введение в ScilabСкачать

scilab. Решение систем обыкновенных дифференциальных уравнений в бесплатном пакете.Скачать

Как решают уравнения в России и США!?Скачать

Как решить уравнение #россия #сша #америка #уравненияСкачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Scilab Лабараторная 1.1Скачать

ЕГЭ по математике. Профильный уровень. Задание 5. Найдите корень уравненияСкачать

How to use ScilabСкачать

🔴 Найдите корень уравнения 2+9x=4x+3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

Практикум по реализации ДУ в ScilabСкачать

Алгоритмы. Нахождение корней уравнения методом хордСкачать