18 февраля 2014
В этом видеоуроке мы рассмотрим решение довольно серьезного логарифмического уравнения, в котором не просто требуется найти корни, но и отобрать те из них, которые лежат на заданном отрезке.
Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.
- Замечание по поводу логарифмический уравнений
- Решение логарифмического уравнения в задаче C1
- Сумма логарифмов и логарифм произведения
- Правила вынесения степеней из логарифма
- Вынесение степени из основания логарифма
- Деление дроби на дробь: дополнительные соображения
- Избавление от знака логарифма
- Отбор корней логарифмического уравнения на отрезке
- Иррациональные корни
- Сравнение иррациональный чисел: универсальный алгоритм
- Логарифмические уравнения
- Как решать логарифмические уравнения подробный разбор примеров
- Сложение и вычитание логарифмов.
- Что такое логарифм и как его посчитать
- Два очевидных следствия определения логарифма
- Свойства логарифмов
- Степень можно выносить за знак логарифма
- Логарифм произведения и логарифм частного
- Формула перехода к новому основанию
- Сумма логарифмов. Разница логарифмов
- Логарифмический ноль и логарифмическая единица
- Как решать уравнения с логарифмами: 2 способа с примерами
- Сравнение логарифмов
- Пример Найдите корень уравнения.
- Логарифмы со специальным обозначением
- Десятичный логарифм
- Натуральный логарифм
- Пример решения логарифмического уравнения с разными основаниями
- Пример решения логарифмического уравнения с переменными основаниями
- Использование свойств логарифмов при решении логарифмических уравнений и неравенств
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Замечание по поводу логарифмический уравнений
Перед тем как переходить непосредственно к уравнению, хочу поделиться небольшой исторической справкой. Дело в том, что ЕГЭ по математике в том виде, котором нам предстоит его сдавать, существует в России уже не первый год. И то уравнение, которое вы сейчас видите на своих экранах, появилось в контрольно-измерительных материалах уже давно.
Однако из года в год ко мне приходят ученики которые пытаются решать вот такие, прямо скажем, непростые уравнения, но при этом не могут понять: с чего им вообще начинать и как подступиться к логарифмам? Такая проблема может возникнуть даже у сильных, хорошо подготовленных учеников.
В результате многие начинают опасаться этой темы, а то и вовсе считать себя тупыми. Так вот, запомните: если у вас не получается решить такое уравнение, это совершенно не значит, что вы — тупые. Потому что, например, вот с таким уравнением вы справитесь практически устно:
А если это не так, вы сейчас не читали бы этот текст, поскольку были заняты более простыми и приземленными задачами. Конечно, кто-то сейчас возразит: «А какое отношение это простейшее уравнение имеет к нашей здоровой конструкции?» Отвечаю: любое логарифмическое уравнение, каким бы сложным оно ни было, в итоге сводится вот к таким простейшим, устно решаемым конструкциям.
Разумеется, переходить от сложных логарифмических уравнений к более простым нужно не с помощью подбора или танцев с бубном, а по четким, давно определенным правилам, которые так и называются — правила преобразования логарифмических выражений. Зная их, вы без труда разберетесь даже с самыми навороченными уравнениями в ЕГЭ по математике.
И именно об этих правилах мы будем говорить в сегодняшнем уроке. Поехали!
Видео:Отбор корней по окружностиСкачать

Решение логарифмического уравнения в задаче C1
Итак, решаем уравнение:
В первую очередь, когда речь заходит о логарифмических уравнениях, вспоминаем основную тактику — если можно выразиться, основное правило решения логарифмических уравнений. Заключается оно в следующем:
. Любое логарифмическое уравнение, что бы в него не входило, какие бы логарифмы, по какому бы основанию, и что бы в себе не c одержали, обязательно нужно привести к уравнению вида:
Если мы посмотрим на наше уравнение, то заметим сразу две проблемы:
- Слева у нас стоит сумма двух чисел, одно из которых вообще не является логарифмом.
- Справа стоит вполне себе логарифм, однако в его основании стоит корень. А у логарифма слева — просто 2, т.е. основания логарифмов слева и справа различаются.
Итак, мы составили этакий список проблем, которые отделяют наше уравнение от того канонического уравнения, к которому нужно привести любое логарифмическое уравнение в процессе решения. Таким образом, решение нашего уравнения на данном этапе сводится к тому, чтобы устранить описанные выше две проблемы.
Любое логарифмическое уравнение решается быстро и легко, если свести его к канонической форме.
Сумма логарифмов и логарифм произведения
Давайте действовать по порядку. Сначала разберемся с конструкцией, которая стоит слева. Что мы можем сказать про сумму двух логарифмов? Давайте вспомним замечательную формулу:
log a f ( x ) + log a g ( x ) = log a f ( x ) · g ( x )
Но стоить учесть, что в нашем случае первое слагаемо вообще не является логарифмом. Значит, нужно представить единицу в виде логарифма по основанию 2 (именно 2, потому что слева стоит логарифм по основанию 2). Как это сделать? Опять вспоминаем замечательную формулу:
Здесь нужно понимать: когда мы говорим «Любое основание b », то подразумеваем, что b все-таки не может быть произвольным числом. Если мы вставляем какое-то число в логарифм, на него сразу накладываются определенные ограничения, а именно: основание логарифма должно быть больше 0 и не должно быть равно 1. Иначе логарифм просто не имеет смысла. Запишем это:
Давайте посмотрим, что происходит в нашем случае:
Теперь перепишем все наше уравнение с учетом этого факта. И сразу же применяем другое правило: сумма логарифмов равна логарифму произведения аргументов. В итоге получим:
Мы получили новое уравнение. Как видим, оно уже гораздо ближе к тому каноническому равнению, к которому мы стремимся. Но есть одна проблема, мы записали ее в виде второго пункта: у наших логарифмов, которые стоят слева и справа, разные основания. Переходим к следующему шагу.
Правила вынесения степеней из логарифма
Итак у логарифма, который стоит слева, основание просто 2, а у логарифма, который стоит справа, в основании присутствует корень. Но и это не является проблемой, если вспомнить, что из оснований из аргументов логарифма можно выносить в степень. Давайте запишем одно из этих правил:
Переведя на человеческий язык: можно выносить степень из основания логарифма и ставить ее спереди в качестве множителя. Число n «мигрировало» из логарифма наружу и стало коэффициентом спереди.
С тем же успехом мы можем вынести степень из основания логарифма. Выглядеть это будет так:
Другими словами, если вынести степень из аргумента логарифма, эта степень также пишется в качестве множителя перед логарифмом, но уже не в виде числа, а в виде обратного числа 1/ k .
Однако и это еще не все! Мы можем объединить две данные формулы и почить следующую формулу:
Когда степень стоит и в основании, и в аргументе логарифма, мы можем сэкономить время и упростить вычисления, если сразу же вынести степени и из основания, и из аргумента. При этом то, что стояло в аргументе (в нашем случае это коэффициент n ), окажется в числителе. А то, что было степенью у основания, a k , отправится в знаменатель.
И именно эти формулы мы сейчас будем применять для того, чтобы свести наши логарифмы к одному и тому же основанию.
Вынесение степени из основания логарифма
Прежде всего, выберем более-менее красивое основание. Очевидно, что с двойкой в основании намного приятней работать, чем с корнем. Таким образом, давайте попробуем привести второй логарифм к основанию 2. Давайте выпишем этот логарифм отдельно:
Что мы можем здесь сделать? Вспомним формулу степени с рациональным показателем. Другими словами, мы можем записать в корни в качестве степени с рациональным показателем. А затем выносим степень 1/2 и из аргумента, и из основания логарифма. Сокращаем двойки в коэффициентах в числителе и знаменателе, стоящих перед логарифмом:
Наконец, перепишем исходное уравнение с учетом новых коэффициентов:
log2 2(9 x 2 + 5) = log2 (8 x 4 + 14)
Мы получили каноническое логарифмическое уравнение. И слева, и справа у нас стоит логарифм по одному и тому же основанию 2. Помимо этих логарифмов никаких коэффициентов, никаких слагаемых ни слева, ни справа нет.
Следственно, мы можем избавиться от знака логарифма. Разумеется, с учетом области определения. Но прежде, чем это сделать, давайте вернемся назад и сделаем небольшое уточнение по поводу дробей.
Деление дроби на дробь: дополнительные соображения
Далеко не всем ученикам понятно, откуда берутся и куда деваются множители перед правым логарифмом. Запишем еще раз:
Давайте разберемся, что такое дробь. Запишем:
А теперь вспоминаем правило деления дробей: чтобы разделить на 1/2 нужно умножить на перевернутую дробь:
Разумеется, для удобства дальнейших вычислений мы можем записать двойку как 2/1 — и именно это мы наблюдаем в качестве второго коэффициента в процессе решения.
Надеюсь, теперь всем понятно, откуда берется второй коэффициент, поэтому переходим непосредственно к решению нашего канонического логарифмического уравнения.
Видео:ЕГЭ база #7 / Логарифмические уравнения / Свойства, определение логарифма / решу егэСкачать

Избавление от знака логарифма
Напоминаю, что сейчас мы можем избавиться от логарифмов и оставить следующее выражение:
2(9 x 2 + 5) = 8 x 4 + 14
Давайте раскроем скобки слева. Получим:
18 x 2 + 10 = 8 x 4 + 14
Перенесем все из левой части в правую:
8 x 4 + 14 − 18 x 2 − 10 = 0
Приведем подобные и получим:
8 x 4 − 18 x 2 + 4 = 0
Можем разделить обе части этого уравнения на 2, чтобы упростить коэффициенты, и получим:
4 x 4 − 9 x 2 + 2 = 0
Перед нами обычное биквадратное уравнение, и его корни легко считаются через дискриминант. Итак, запишем дискриминант:
D = 81 − 4 · 4 · 2 = 81 − 32 = 49
Прекрасно, Дискриминант «красивый», корень из него равен 7. Все, считаем сами иксы. Но в данном случае корни получатся не x , а x 2 , потому что у нас биквадратное уравнение. Итак, наши варианты:
Обратите внимание: мы извлекали корни, поэтому ответов будет два, т.к. квадрат — функция четная. И если мы напишем лишь корень из двух, то второй корень мы просто потеряем.
Теперь расписываем второй корень нашего биквадратного уравнения:
Опять же, мы извлекаем арифметический квадратный корень из обеих частей нашего уравнения и получаем два корня. Однако помните:
Недостаточно просто приравнять аргументы логарифмов в канонической форме. Помните об области определения!
Итого мы получили четыре корня. Все они действительно являются решениями нашего исходного уравнения. Взгляните: в нашем исходном логарифмическом уравнении внутри логарифмов стоит либо 9 x 2 + 5 (эта функция всегда положительна), либо 8 x 4 + 14 — она тоже всегда положительна. Следовательно, область определения логарифмов выполняется в любом случае, какой бы корень мы не получили, а это значит, что все четыре корня являются решениями нашего уравнения.
Прекрасно, теперь переходим ко второй части задачи.
Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

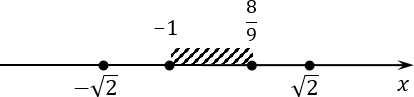
Отбор корней логарифмического уравнения на отрезке
Отбираем из наших четырех корней те, которые лежат на отрезке [−1; 8/9]. Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:
Обе точки будут закрашенные. Т.е. по условию задачи нас интересует заштрихованный отрезок. Теперь давайте разбираться с корнями.
Иррациональные корни
Начнем с иррациональных корней. Заметим, что 8/9 x = 1/2 и x = −1/2. Давайте заметим, что левый конец отрезка (−1) — отрицательный, а правый (8/9) — положительный. Следовательно, где-то между этими концами лежит число 0. Корень x = −1/2 будет находиться между −1 и 0, т.е. попадет в окончательный ответ. Аналогично поступаем с корнем x = 1/2. Этот корень также лежит на рассматриваемом отрезке.
Убедиться, что число 8/9 больше, чем 1/2, можно очень просто. Давайте вычтем эти числа друг из друга:
Получили дробь 7/18 > 0, а это по определению означает, что 8/9 > 1/2.
Давайте отметим подходящие корни на оси координат:
Окончательным ответом будут два корня: 1/2 и −1/2.
Видео:Отбор корней по окружностиСкачать

Сравнение иррациональный чисел: универсальный алгоритм
В заключении хотел бы еще раз вернуться к иррациональным числам. На их примере мы сейчас посмотрим, как сравнивать рациональные и иррациональные величины в математике. Для начала по между ними вот такую галочку V — знак «больше» или «меньше», но мы пока не знаем, в какую сторону он направлен. Запишем:
Зачем вообще нужны какие-то алгоритмы сравнения? Дело в том, что в данной задаче нам очень повезло: в процессе решения возникло разделяющее число 1, про которое мы точно можем сказать:
Однако далеко не всегда вы с ходу увидите такое число. Поэтому давайте попробуем сравнить наши числа «в лоб», напрямую.
Как это делается? Делаем то же самое, что и с обычными неравенствами:
- Сначала, если бы у нас где-то были отрицательные коэффициенты, то мы умножили бы обе части неравенства на −1. Разумеется, поменяв при этом знак. Вот такая галочка V изменилась бы на такую — Λ.
- Но в нашем случае обе стороны уже положительны, поэтому ничего менять не надо. Что действительно нужно, так это возвести обе части в квадрат, чтобы избавится от радикала.
Если при сравнении иррациональных чисел не удается с ходу подобрать разделяющий элемент, рекомендую выполнять такое сравнение «в лоб» — расписывая как обычное неравенство.
При решении это оформляется вот таким образом:
Теперь это все легко сравнивается. Дело в том, что 64/81 a или b , именно логарифм, равный другому логарифму.
Кроме того, основания логарифмов также должны быть равны. При этом если уравнение составлено грамотно, то с помощью элементарных логарифмических преобразований (сумма логарифмов, преобразование числа в логарифм и т.д.) мы сведем это уравнение именно к каноническому.
Поэтому впредь, когда вы видите логарифмическое равнение, которое не решается сразу «в лоб», не стоит теряться или пробовать подобрать ответ. Достаточно выполнить следующие шаги:
- Привести все свободные элементы к логарифму;
- Затем эти логарифмы сложить;
- В полученной конструкции все логарифмы привести к одному и тому же основанию.
В результате вы получите простое уравнение, которое решается элементарными средствами алгебры из материалов 8—9 класса. В общем, заходите на мой сайт, тренируйтесь решать логарифмы, решайте логарифмические уравнения как я, решайте их лучше меня. А у меня на этом все. С Вами был Павел Бердов. До новых встреч!
Видео:Решение логарифмических уравнений #shortsСкачать

Логарифмические уравнения
Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.
Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.
При этом 0,;a> 0,;aneq 1′ alt=’b> 0,;a> 0,;aneq 1′ />.
Обратим внимание на область допустимых значений логарифма:
Основное логарифмическое тождество:
Основные формулы для логарифмов:
(Логарифм произведения равен сумме логарифмов)
(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)
Формула перехода к новому основанию:
Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.
Все это пригодится нам в решении логарифмических уравнений.
Простейшие логарифмические уравнения
Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.
Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при 0,;a> 0,;aneq 1′ alt=’b> 0,;a> 0,;aneq 1′ />.
Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.
2. Решите уравнение:
В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.
3. Решите уравнение:
Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.
4. Решите уравнение:
Область допустимых значений: 0.’ alt=’4+x> 0.’ /> Значит, -4.’ alt=’x> -4.’ />
Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом -4′ alt=’x> -4′ />.
5. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
0\ x^-4> 0\ x^+x=x^-4 endright.Leftrightarrow left <beginx^+x> 0\ x^-4> 0\ x=-4 endright.Leftrightarrow x=-4′ alt=’log _left ( x^+x right )=log _left ( x^-4 right )Leftrightarrow left <beginx^+x> 0\ x^-4> 0\ x^+x=x^-4 endright.Leftrightarrow left <beginx^+x> 0\ x^-4> 0\ x=-4 endright.Leftrightarrow x=-4′ />
Ответ: –4.
Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Запишем решение как цепочку равносильных переходов.
0 endright.Leftrightarrow left <beginleft (2^<log _left ( 4x+5 right )> right )^<frac>=9\ x> -1frac endright.Leftrightarrow left <beginleft ( 4x+5 right )^<frac>=9\ x> -1frac endright.Leftrightarrow left <beginsqrt=9\ x> -1frac endright.Leftrightarrow left <begin4x+5=81\ x> -1frac endright.Leftrightarrow left <beginx=19\ x> -1frac endright.’ alt=’2^<log _left ( 4x+5 right )>=9Leftrightarrow left <begin2^frac<<log _left ( 4x+5 right )>>=9\ 4x+5> 0 endright.Leftrightarrow left <beginleft (2^<log _left ( 4x+5 right )> right )^<frac>=9\ x> -1frac endright.Leftrightarrow left <beginleft ( 4x+5 right )^<frac>=9\ x> -1frac endright.Leftrightarrow left <beginsqrt=9\ x> -1frac endright.Leftrightarrow left <begin4x+5=81\ x> -1frac endright.Leftrightarrow left <beginx=19\ x> -1frac endright.’ />
Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.
ОДЗ:
0\ x> 0\ xneq 1 endright.’ alt=’left <begin12-x> 0\ x> 0\ xneq 1 endright.’ />
Теперь можно «убрать» логарифмы.
— посторонний корень, поскольку должно выполняться условие 0′ alt=’x> 0′ />.
8. Решите уравнение .
ОДЗ уравнения: 0′ alt=’x> 0′ />
Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.
Вернемся к переменной х:
Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.
Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.
Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену
Вернемся к переменной х. Получим:
. Мы нашли все корни исходного уравнения.
Логарифмические уравнения могут встретиться вам и в задании №1 Профильного ЕГЭ по математике, и в задании №12. И если в задании №1 нужно решить простейшее уравнение, то в задаче 12 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Как решать логарифмические уравнения подробный разбор примеров
Видео:Задание №13. Как отбирать корни в тригонометрической окружности? 🤔Скачать

Сложение и вычитание логарифмов.
Возьмем два логарифма с одинаковыми основаниями: loga x и loga y. Тогда сними возможно выполнять операции сложения и вычитания:
Как видим, сумма логарифмов равняется логарифму произведения, а разность логарифмов – логарифму частного. Причем это верно если числа а, х и у положительны и а ≠ 1.
Важно обращать внимание, что основным аспектом в данных формулах выступают одни и те же основания. Если основания отличаются друг от друга, эти правила не применимы!
Правила сложения и вычитания логарифмов с одинаковыми основаниями читаются не только с лева на право, но и на оборот. В результате мы имеем теоремы логарифма произведения и логарифма частного.
Логарифм произведения двух положительных чисел равен сумме их логарифмов; перефразируя данную теорему получим следующее, если числа а, x и у положительны и а ≠ 1, то:
Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя. Говоря по другому, если числа а, х и у положительны и а ≠ 1, то:
Применим вышеизложенные теоремы для решения примеров:
Если числа x и у отрицательны, то формула логарифма произведения становится бессмысленной. Так, запрещено писать:
так как выражения log2(-8) и log2(-4) вообще не определены (логарифмическая функция у = log2х определена лишь для положительных значений аргументах).
Теорема произведения применима не только для двух, но и для неограниченного числа сомножителей. Это означает, что для всякого натурального k и любых положительных чисел x1, x2, . . . ,xn существует тождество :
Из теоремы логарифма частного можно получить еще одно свойство логарифма. Общеизвестно, что loga1= 0, следовательно,
А значит имеет место равенство:
Логарифмы двух взаимно обратных чисел по одному и тому же основанию будут различны друг от друга исключительно знаком. Так:
Видео:Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Что такое логарифм и как его посчитать
Логарифм имеет следующий вид:

b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X. 

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:

Видео:Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать

Два очевидных следствия определения логарифма
log a 1 = 0 ( a > 0, a ≠ 1 )
Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень – единицу.
Видео:Нахождение корней уравнения, принадлежащих промежуткуСкачать

Свойства логарифмов
Перечисленные ниже свойства логарифмов вытекают из основного логарифмического тождества:
 |  | ||||||||||||||
 |  | ||||||||||||||
 |  | ||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | ( формула перехода к новому основанию логарифмов ), | ||||||||||||||
 | |||||||||||||||
 |
Видео:Круговорот воды в природе ➜ Решение логарифмических уравнений из ЕГЭ #ShortsСкачать  Степень можно выносить за знак логарифмаИ вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример: log a ( f ( x ) 2 = 2 log a f ( x ) Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть – только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени. Видео:Логарифмические уравнения. 11 класс.Скачать  Логарифм произведения и логарифм частногоlog a b c = log a b − log a c ( a > 0, a ≠ 1, b > 0, c > 0 ) Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании “слева направо” происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного – расширение ОДЗ. log a ( f ( x ) g ( x ) ) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля. Преобразуя данное выражение в сумму log a f ( x ) + log a g ( x ) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6). Видео:Логарифмы с Нуля, Что Такое Логарифм? + ДЗ (ЕГЭ 2024 Математика Профиль и База, 10 и 11 класс)Скачать  Формула перехода к новому основаниюТот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной. Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8): log a b = 1 log b a ( a > 0, a ≠ 1, b > 0, b ≠ 1 ) Видео:Логарифмы в ЕГЭ🫢 Решишь второй?!Скачать  Сумма логарифмов. Разница логарифмовЛогарифмы с одинаковыми основаниями можно складывать: Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя! Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать  Логарифмический ноль и логарифмическая единицаЭто следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор. Запомните, что логарифм от a по основанию а всегда равен единице: loga a = 1 – это логарифмическая единица. Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a 0 = 1: loga 1 = 0 – логарифмический ноль. Видео:Интересная задача на логарифмы в ЕГЭСкачать  Как решать уравнения с логарифмами: 2 способа с примерамиРешить логарифмическое уравнение можно разными способами. Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида: При решении логарифмических уравнений важно помнить об области определения логарифма, т.к. аргумент f(x) должен быть больше ноля. Поэтому после решения логарифмического уравнения мы всегда делаем проверку! Давайте посмотрим, как это работает на примере: Воспользуемся определением логарифма и получим: Теперь перед нами простейшее уравнение, решить которое не составит труда: Сделаем проверку. Подставим найденный Х в исходное уравнение: Основной минус данного метода решения логарифмических уравнений в том, что многие ребята путают, что именно нужно возводить в степень. То есть при преобразовании logaf(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ. Поэтому мы покажем еще один способ решения логарифмических уравнений. Чтобы решить логарифмическое уравнение, нам нужно привести его к такому виду, когда и в правой, и в левой части уравнения будут стоять логарифмы с одинаковыми основаниями. Это выглядит вот так: Когда уравнение приведено к такому виду, то мы можем «зачеркнуть» логарифмы и решить простое уравнение. Давайте разбираться на примере. Решим еще раз то же самое уравнение, но теперь этим способом: Для этого вспоминаем свойства логарифмов. Первое свойство, которое нам здесь понадобится – это логарифмическая единица. Напомним его: Воспользуемся этим свойством в нашем случае, получим: Да, действий в этом способе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего шансов ошибиться меньше. К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений. Разберем другой пример: Теперь делаем проверку: Еще один пример решения логарифмического уравнения:
Теперь подставим х2 = -5 в исходное уравнение: Видео:Умножаем логарифмы В УМЕ🧠Скачать  Сравнение логарифмов
| ||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
|
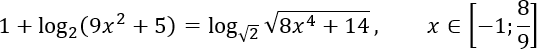
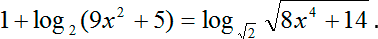
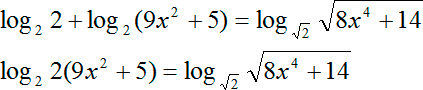
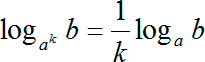
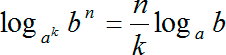
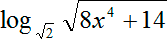
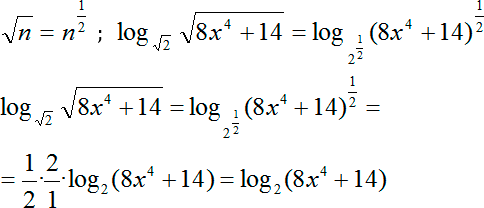
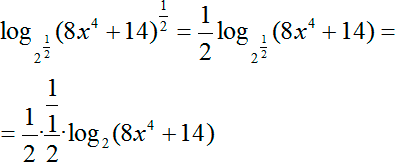
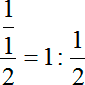
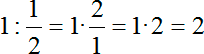
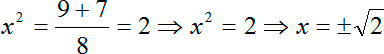


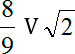
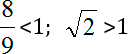
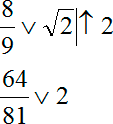

























 Логарифмы с одинаковыми основаниями можно вычитать:
Логарифмы с одинаковыми основаниями можно вычитать: 
 Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
 Вспоминаем определение логарифма и получаем следующее:
Вспоминаем определение логарифма и получаем следующее:  Вспоминаем определение логарифма и получаем следующее: Таким образом мы получаем простое уравнение, которое сможем легко решить.
Вспоминаем определение логарифма и получаем следующее: Таким образом мы получаем простое уравнение, которое сможем легко решить.
 Так как 3 2 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Так как 3 2 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
 В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.
В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2. То есть в нашем случае:
То есть в нашем случае:  То есть в нашем случае: Возьмем правую часть нашего уравнения и начнем ее преобразовывать:
То есть в нашем случае: Возьмем правую часть нашего уравнения и начнем ее преобразовывать: Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
 Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили:
Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили: Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение:
Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение: Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:
Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:  Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом: После преобразования правой части наше уравнение принимает следующий вид:
Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом: После преобразования правой части наше уравнение принимает следующий вид:  Теперь можно зачеркнуть логарифмы и тогда получим:
Теперь можно зачеркнуть логарифмы и тогда получим:  Теперь можно зачеркнуть логарифмы и тогда получим: Вспоминаем свойства степеней:
Теперь можно зачеркнуть логарифмы и тогда получим: Вспоминаем свойства степеней: то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
то последнее выражение верно. Следовательно, х = 3 является корнем уравнения. Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:
Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:  Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим: Теперь преобразуем правую часть уравнения:
Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим: Теперь преобразуем правую часть уравнения:  Выполнив преобразования правой и левой частей уравнения, мы получили:
Выполнив преобразования правой и левой частей уравнения, мы получили:  Выполнив преобразования правой и левой частей уравнения, мы получили: Теперь мы можем зачеркнуть логарифмы:
Выполнив преобразования правой и левой частей уравнения, мы получили: Теперь мы можем зачеркнуть логарифмы: Решим данное квадратное уравнение, найдем дискриминант:
Решим данное квадратное уравнение, найдем дискриминант: Сделаем проверку, подставим х1 = 1 в исходное уравнение:
Сделаем проверку, подставим х1 = 1 в исходное уравнение:  Сделаем проверку, подставим х1 = 1 в исходное уравнение:
Сделаем проверку, подставим х1 = 1 в исходное уравнение:  Верно, следовательно, х1 = 1 является корнем уравнения.
Верно, следовательно, х1 = 1 является корнем уравнения. Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень.
Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень.










 Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.
Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.



 Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
 Применяем эти знания и получаем:
Применяем эти знания и получаем:  Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:  Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма: Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:
Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:  Делаем проверку:
Делаем проверку:  Делаем проверку: Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим:
Делаем проверку: Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим: Верно, следовательно, х = 4 является корнем уравнения.
Верно, следовательно, х = 4 является корнем уравнения. Преобразуем правую часть уравнения:
Преобразуем правую часть уравнения:  Преобразуем правую часть уравнения: Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:
Преобразуем правую часть уравнения: Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:  Теперь мы можем зачеркнуть логарифмы:
Теперь мы можем зачеркнуть логарифмы:  Теперь мы можем зачеркнуть логарифмы: Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:
Теперь мы можем зачеркнуть логарифмы: Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:


 Перепишем нашу систему:
Перепишем нашу систему:  Перепишем нашу систему: Следовательно, наша система примет следующий вид:
Перепишем нашу систему: Следовательно, наша система примет следующий вид:  Теперь решаем наше уравнение:
Теперь решаем наше уравнение:  Теперь решаем наше уравнение: Справа у нас квадрат суммы:
Теперь решаем наше уравнение: Справа у нас квадрат суммы: Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.
Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.