9 -е занятие по MATLAB
ЛАБОРАТОРНАЯ РАБОТА № 9
Синтез наблюдающего устройства
для стационарной линейной системы управления.
Цель работы: освоение методов синтеза асимптотического наблюдающего устройства (наблюдателя) для стационарной линейной системы управления со скалярным управлением при отсутствии случайных помех. Анализ динамических свойств системы с наблюдателем.
I. Синтез наблюдателя на основе модального управления.
Наблюдающим устройством называется динамическая система, которая восстанавливает вектор состояния заданной системы на основе измерения входного и выходного воздействий при известной структуре (матрицы А, В, С) заданной системы.
Если система, для которой восстанавливается полный вектор состояния, описывается векторным уравнением

то наблюдатель имеет следующее уравнение:

где u — скалярное входное управляющее воздействие, 


Наблюдатель будет называться асимптотическим, если

где 
Вычитая из первого уравнения (1) второе (2), получим уравнение относительно ошибки восстановления

Для выполнения соотношения (3) необходимо так подобрать (синтезировать) матрицу наблюдателя 

Для системы (1) со скалярным управлением (с одним входным воздействием) рассчитаем матрицу 
Характеристическое уравнение для определения собственных чисел матрицы 

Известно, что собственные числа матрицы не изменятся, если эту матрицу транспонировать. Поэтому корни характеристического уравнения (5) также не изменятся, если оно будет записано для транспонированной матрицы 

Уравнение (6) может отвечать следующей системе:

с модальным управлением

т.е. замкнутая система (7) на управление (8) имеет вид

для которой характеристическое уравнение будет аналогично (6):

Система (7) является дуальной к системе (1) в смысле Калмана.
Таким образом, если будет рассчитано модальное управление для системы (7), то матрица коэффициента усиления 

где T — символ транспонирования.
Расчет модального управления начинается с приведения системы (7) к каноническом виду с помощью матрицы преобразования подобия N :

где 

Расчет матрицы 
Модальное управление 

где 


с желаемыми корнями 
Переход к требуемой матрице усиления наблюдателя осуществляется следующим образом:


Расчет матрицы усиления наблюдателя сводится к следующим этапам:
1) Проверка системы на полную наблюдаемость по Калману;
2) Определение коэффициентов характеристического уравнения системы (1);
3) Задание желаемых корней в левой полуплоскости и определение коэффициентов характеристического уравнения (16);
4) Расчет матрицы 
5) Расчет матрицы преобразования подобия по соотношениям (13), (14);
6) Собственно расчет матрицы усиления наблюдателя по выражению (18).
Пример 1. Синтез наблюдателя для линейной системы 3-го порядка, заданной передаточной функцией вида

Знаменатель передаточной функции определяет собой и характеристическое уравнение заданной системы с коэффициентами

В системе MATLAB коэффициенты характеристического уравнения можно определить с помощью встроенной функции poly , которая определяет и коэффициент при старшей степени комплексной переменной. Для (19):
1.0000 1.7500 0.8750 0.1250
С помощью функции poly можно определить и коэффициенты системы управления, заданной в пространстве состояний.
С учетом (19) запишем модель объекта управления в пространстве состояний, полагая 

Матрицы объекта управления в соответствии с (21) имеют вид

Уравнение выхода примем в виде 

Проверка объекта управления на полную наблюдаемость:

Определение коэффициентов характеристического уравнения по заданным корням:
где i — мнимая единица,

т.е. 
Для вычисления коэффициентов уравнения можно применить poly от вектора заданных корней, т.е. poly([ l 1 ; l 2 ; l 3 ]) .
Расчет матрицы 

Расчет матрицы преобразования подобия 


Расчет матрицы усиления наблюдателя:


— проверить корни характеристического уравнения ошибки восстановления.
— решить дифференциальное уравнение ошибки восстановления со следующими начальными условиями: 
— синтезировать наблюдатель с другими задаваемыми корнями характеристического уравнения ошибки: ; .
II. Синтез модального управления при не полностью известном векторе состояния системы .
Синтезируем модальное управление для системы (21) вида

где 

В соответствии с теоремой разделимости матрицу 
1) Проверка объекта управления на полную управляемость по Калману:

2) Расчет матрицы преобразования подобия N :

3) Задание собственных чисел матрицы замкнутой системы:
4) Определение коэффициентов характеристического уравнения замкнутой системы:


5) Расчет матрицы модального управления для канонической системы

6) Расчет матрицы модального управления 

7) Анализ системы с модальным управлением и наблюдающим устройством.
Система дифференциальных уравнений в матричном виде:

где А, В, С — матрицы объекта и выхода определяются по (22), (23); 





В системе MATLAB решение (33) может быть принято в виде:
% Сначала создается М-файл как М-функция под именем, например, difn1
A =[0 1 0;0 0 1;-0.125 -0.875 -1.75];
K =[64.5401 43.1549 8.1540];
% Сценарий решения дифуравнения (3) под именем didn11
plot(t,z),grid,legend( ‘x_1’ , ‘x_2’ , ‘x_3’ , ‘xv_1’ , ‘xv_2’ , ‘xv_3’ ),
где ‘x_1′,’x_2′,’x_3’ — переменные состояния системы управления,
‘xv_1′,’xv_2′,’xv_3’ — переменные состояния наблюдателя.
— построить графики переходных процессов для соответствующих пар переменных состояния объекта управления и наблюдателя.
— построить переходные процессы системы (33) для различных значений начальных условий: , , .
— написать программу, совмещающую в себе синтез модального управления, синтез наблюдателя и анализ переходных процессов системы управления с асимптотическим наблюдающим устройством.
III. Синтез модального управления и наблюдающего устройства для неустойчивого объекта в системе MATLAB.
Дано: передаточная функция неустойчивого объекта управления

Требуется синтезировать асимптотически устойчивую систему с обратной связью по состоянию при не полностью известном векторе состояния объекта.
Задача заключается в синтезе модального управления и асимптотического наблюдающего устройства.
% Анализ переходного процесса по заданной передаточной функции (34)
» step(W2),grid,ylabel (‘Амплитуда выходной координаты объекта’)
% Описание объекта управления в пространстве состояний
% Выделение матриц A, B, C, D объекта управления по заданной системе пространства состояний s1
% Проверка объекта на полную управляемость и полную наблюдаемость
» с t 1=ctrb(s1) % Формирование матрицы управляемости
» rank( ct 1) % Вычисление ранга матрицы управляемости
»o b 1=obsv(s1) % Формирование матрицы наблюдаемости
» rank( ob 1) % Вычисление ранга матрицы наблюдаемости
% Так как ранг матрицы управляемости и ранг матрицы наблюдаемости равен трем, то объект полностью управляем и полностью наблюдаем, поскольку размерность объекта также равна третьему порядку.
3 . 1. Синтез модального управления вида 
% Матрицы объекта принимаем из системы s1: s1=ss(W2)
» P 1=[-3;-5+4*i;-5-4*i]; % Желаемый вектор собственных значений
» [Kр]=acker(A,B,P1) % Для объектов с одним входным воздействием
11.7500 70.8750 123.1250
% Исследование синтезированной системы
» s2=ss(A-B*K,B,C,D); % Формирование системы с регулятором
% Анализ переходного процесса синтезированной системы
% Переходный процесс является установившимся, т.е. система устойчивая
— исследовать переходные процессы синтезированной системы на основе решения системы дифференциальных уравнений с помощью ode45 .
— исследовать переходные процессы синтезированной системы с помщью команды lsim .
3.2. Синтез асимптотического наблюдателя.
% Определение коэффициентов характеристического уравнения объекта, заданного передаточной функцией или представленного в пространств состояний
» a= poly(W2) % Можно применить и poly( s1 )
1.0000 1.2500 0.1250 -0.1250
% Коэффициенты характеристического уравнения объекта равны:
% Сформируем вектор-строку коэффициентов a012:
-0.1250 0.1250 1.2500
% Определение коэффициентов характеристического уравнения ошибки восстановления по желаемым корням
» P 2=[-1;-1.5;-2]; % Вектор желаемых корней
1.0000 4.5000 6.5000 3.0000
% Коэффициенты характеристического уравнения ошибки равны:
% Сформируем вектор-строку коэффициентов d012:
3.0000 6.5000 4.5000
% Формирование модальной матрицы 
3.1250 6.3750 3.2500
Расчет матрицы преобразования подобия 
[A,B,C,D]=ssdata(s1); %Выделение матриц из заданной системы
»N1=[0 0 1]*inv([C’ A’*C’ A’^2*C’]) % Формирование вспомогательной матрицы
0.5547 0.2427 -0.4160
% Расчет матрицы усиления наблюдателя:
Задание. Для системы с модальным управлением и наблюдателем выполнить следующее:
— исследовать переходные процессы в системе (35) с помощью step

— исследовать переходные процессы в системе (35) с помощью lsim
IV. Синтез модального управления и наблюдающего устройства для неустойчивого объекта с векторным входом и векторным выходом в системе MATLAB.
Дано: система дифференциальных уравнений с тремя управляющими воздействиями

Матрицы А, В, С, D :

Матрицу С задали так, чтобы иметь векторный выход
Система (36) неустойчивая:
» eig(A) % Вычисление собственных чисел матрицы А
0.5000 % Положительное собственное число обуславливает неустойчивость
% Анализ переходного процесса в неустойчивой системе по функции lsim
» u1=ones(size(T(:))); % Формирование единичной функции времени
» u2=ones(size(T(:))); % Формирование единичной функции времени
» u3=ones(size(T(:))); % Формирование единичной функции времени
» U=[u1,u2,u3]; % Вектор управляющих воздействий
» lsim(A,B,C,D,U,T),grid,title(‘Исходная неустойчивая система’)
% Переходные процессы по выходным координатам стремяться к бесконечности
Требуется синтезировать асимптотически устойчивую систему с обратной связью по состоянию при не полностью известном векторе состояния объекта.
Синтез модального управления по функции place
% Задаем вектор Р желаемых собственных значений
% Определяем матрицу Kr модального управления
% Исследуем переходные процессы системы с модальным управлением
» u1=ones(size(T(:))); % Формирование единичной функции времени
» u2=ones(size(T(:))); % Формирование единичной функции времени
» u3=ones(size(T(:))); % Формирование единичной функции времени
» U=[u1,u2,u3]; % Вектор управляющих воздействий
» lsim(A- B*Kr ,B,C,D,U,T),grid,title(‘Система с модальным управлением’)
— с помощью расчетного режима функции lsim построить графики переходных процессов исходной системы по переменным вектора выхода в одной системе координат.
— то же самое выполнить для системы с модальным управлением.
Если полный вектор состояния не может быть использован в цепи обратной связи модального управления, то необходимо синтезировать наблюдатель, который формирует оценку вектора состояния.
Синтез асимптотического наблюдателя.
% Задаем вектор Pn собственных значений матрицы системы ошибки восстановления
% Вычисляем матрицу модального управления для дуальной системы
» Kn=Knt’ % Операция транспонирования
Kn = [0, 0;1.2, 0;3, 0.5] % Матрица усиления наблюдателя
% Анализ переходных процессов относительно ошибки восстановления, т.е.

где 
% Зададим начальные условия по
% Для построения переходных процессов используем initial
% Зададим матрицу Се выхода системы ошибки
» Ce=[1 0 0;0 1 0;0 0 1];
% При задании формата initial принимем матрицу В=0 и матрицу D=0 соответствующих размерностей
— синтезировать матрицу усиления наблюдателя для различных задаваемых собственных значений системы (38): , , , .
— применить числовой режим функции initial и построить в одной системе координат переходные процессы по всем переменным состояния ошибки.
Анализ синтезированной системы с асимптотическим наблюдателем.
В задачу входит построение переходных процессов синтезированной системы с наблюдателем и сравнение получаемых процессов для системы с модальным управлением без наблюдающего устройства.
Система с модальным управлением без наблюдающего устройства:

Считается, что вектор состояния Х (t) доступен для измерений в целях реализации закона управления
Для анализа переходных процессов по отработке начальных условий зададим следующий вектор начальных состояний:
Задание. Составить программу для анализа (39) по программе для (38).
Система с модальным управлением и с наблюдающим устройством:

Анализ переходных процессов в (40):
% Задание вектора начальных условий
» Z0=[1;2;3;0;0;0]; % Первые три элемента по 
% Формирование коагулированной матрицы A0 системы (40) по известным матрицам и вычисленным
» Kr = [ 4 , 7.6 , 0 ; -2.8 , 2.75 , 0 ; 0 , 1 , 3.6 ];
» A0=[A,-B*Kr;Kn*C, (A-B*Kr-Kn*C)]; % Размер А0 равен 6 ´ 6
% Формирование вспомогательной матрицы С0 для определения характера изменения каждой переменной состояния системы (40)
» С0=eye(size(A0)) ; % Единичная матрица от размера А0 (здесь 6 ´ 6)
% Формирование вспомогательной матрицы В0 системы (40), которая равна нулю
» B0=zeros(length(A0(:,1)),length(A0(:,length(B(1,:))))) ; % размер n ´ r ( здесь 6 ´ 6)
% Формирование вспомогательной матрицы D 0 системы (40), которая равна нулю
% Применение функции initial для анализа переходных процессов (40)
» initial( A0 , B0,C0,D0 , Z 0) % Процессы по всем переменным
Анализ попарных переходных процессов в числовом режиме initial с формированием отдельных графических окон — figure
% Y0 — вектор выхода системы (40), Z — вектор состояния системы (40)
» figure(1),plot(t,Y0),grid,,title(‘Вектор выхода’), figure(2),plot(t,Z),grid,title(‘Вектор состояния’)
% Можно каждый из графических окон можно описывать отдельно
% Пример попарного представления в различных окнах
— изменить вспомогательную матрицу С0 и проанализировать переходные процессы по Y0 и Z в соответствии с (41).
— попарно сравнить переходные процессы по Х(t) в системе (40) и в системе (39).
Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Анализ устойчивости с помощью MATLAB
Этот раздел мы начнем с критерия Рауса-Гурвица и покажем, какое простое и удобное средство предоставляет MATLAB для вычисления корней характеристического уравнения. Если характеристическое уравнение содержит один варьируемый параметр, то можно отразить в виде диаграммы изменение положения корней в зависимости от этого параметра.
В данном разделе будет введена функция for, с помощью которой последовательность инструкций повторяется заданное число раз.
Критерий Рауса-Гурвица. Как было отмечено выше, критерий Рауса-Гурвица определяет необходимое и достаточное условие устойчивости. Если задано характеристическое уравнение с постоянными коэффициентами, то с помощью критерия Рауса-Гурвица можно определить число корней, расположенных в правой полуплоскости. Например, рассмотрим характеристическое уравнение замкнутой системы, изображенной на рис. 6.10:
q(s) = s3 + s2 + 2s + 24 = 0 .
Замкнутая система управления с передаточной функцией As) = y[s)/ff(s) =
= l/Cs3 + s2 + 2s + 24)
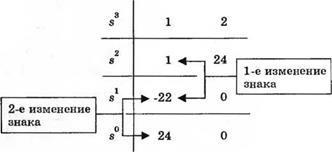
Соответствующая таблица Рауса приведена на рис. 6.11. Два изменения знака в первом столбце указывают на наличие двух корней уравнения в правой полуплоскости; следовательно, замкнутая система неустойчива. С помощью MATLAB мы можем проверить этот результат, непосредственно вычислив корни характеристического уравнения, как это показано на рис. 6.12. Для этого необходимо использовать функцию pole, которая вычисляет корни алгебраического полинома.
Таблица Рауса для замкнутой системы с передаточной функцией 7s) = 1AS3 + s2 + 2s + 24)
Использование функции pole для вычисления полюсов замкнутой системы, изображенной на рис. 6.10
»numg=[1]; deng=[1 1 2 23]; sysg=tf(numg, deng);
1 0000 + 2 8 попадают в правую полуплоскость.
Программа на рис. 6.14 содержит функцию for. Эта функция обеспечивает выполнение одной и той же серии инструкций заданное число раз. Она в сочетании с инструкцией end образует цикл повторяющихся вычислений. На рис. 6.15 приведен формат функции for, а также пример ее использования. В примере цикл повторяется 10 раз. На /-м шаге, где 1 0. Это значит, что мы можем ограничить область поиска значениями 0 0. Сначала с помощью MATLAB мы найдем границу устойчивости в плоскости параметров К и а. Затем мы сможем найти пары значений (К, а), принадлежащих области устойчивости, таких, которые удовлетворяли бы ограничению на установившуюся ошибку. Эта процедура, показанная на рис. 6.16, включает в себя задание диапазона значений К и а и вычисление корней характеристического уравнения для конкретных значений этих параметров. Для каждого К мы найдем первое значение а, при котором по крайней мере один корень характеристического уравнения попадает в правую полуплоскость. Этот процесс повторяется до тех пор, пока не будет пройден весь диапазон значений К и а. Найденные пары чисел (К’, а) определяют границу между областями устойчивости и неустойчивости.
На рис. 6.16 область слева от графика зависимости а =/(К) является областью устойчивости. Если считать, что r(t) = At, I > 0, то установившаяся ошибка
Видео:Решение произвольных уравнений. Методы вычислений в MATLAB. Часть 1. Урок 61Скачать

Найти корни характеристического уравнения матричной функции в MATLAB
У меня есть матрица, которая является функцией некоторого параметра A = A (x). Я бы хотел найти точки x, где эта матрица становится сингулярной. Пример (хотя у меня есть большая матрица):
До сих пор я символически вычислял определитель матрицы, а затем использовал fzero или newtzero для нахождения корней этого характеристического уравнения. Т.е.
Тогда я нашел это: Как узнать, является ли матрица единственной? , где он не должен использовать детерминант ни при каких обстоятельствах.
Действительно, расчет символической детерминанты ужасно медленный. Однако я попытался использовать rank (A), как это было предложено в ссылке, и, похоже, это не работает для символических матриц.
Есть ли способ реализовать предложения в ссылке для нахождения корней характеристического уравнения матрицы, которое дается символически?
Возможным подходом было бы следующее: квадратная матрица A является сингулярной тогда и только тогда, когда однородная линейная (по отношению к вектору y ) система A*y = 0 имеет нетривиальные решения y 0 (что эквивалентно det(A) = 0 и rank(A) = 0 Таким образом, более или менее стандартный, как я помню из прошлого, метод вычисления таких точек х — это решение нелинейной системы
Таким образом, вы можете вычислить точку x* и вектор y* такой, что A(x*) сингулярно, а y* — собственный вектор, отвечающий нулевому собственному значению A(x*) .
Если я правильно помню, вы также можете решить несколько более простую систему
где c — «почти» любой ненулевой случайный вектор (нормализовать его до 1, чтобы избежать числовых задач).
На самом деле существует огромная библиография на эту тему — вы можете искать вычисления бифуркации седло-узла (в случае, если A(x) является якобианом векторного поля) или для «расстояния до неустойчивости».
📸 Видео
ТАУ. Matlab/Simulink - моделирование передаточной функции, снятие характеристикСкачать
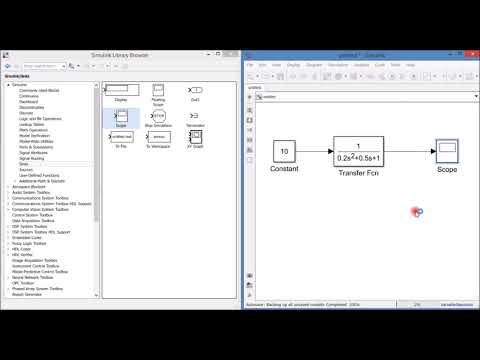
MatLab. Решение дифференциального уравнения.Скачать

ТАУ. Matlab/SIMULINK Фазовые портреты нелинейных и линейных диф. уравненийСкачать

Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

1 - Решение систем нелинейных уравнений в MatlabСкачать

ТАУ. Matlab/SIMULINK Фазовые портреты систем нелинейных диф. уравненийСкачать

Обучение в MATLAB и Simulink: от уравнения к фундаментальным принципамСкачать

Символьные и численные расчеты в MATLABСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

MATLAB 07 Интерактивное построение графиковСкачать

MatLab Простые рекуррентные вычисленияСкачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

Процесс идентификации в MatLabСкачать

Как создавать функции в MATLABСкачать