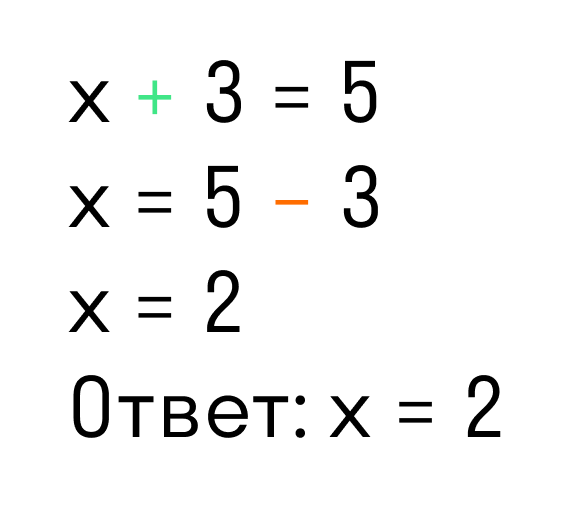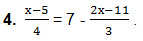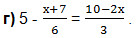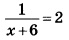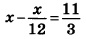Как найти корень линейного уравнения 9 класс

О чем эта статья:

Видео:Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Видео:ОГЭ по математике. Решаем уравнения | МатематикаСкачать

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:

если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;

если а = 0 — уравнение корней не имеет;

если а и b равны нулю, то корнем уравнения является любое число.

Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

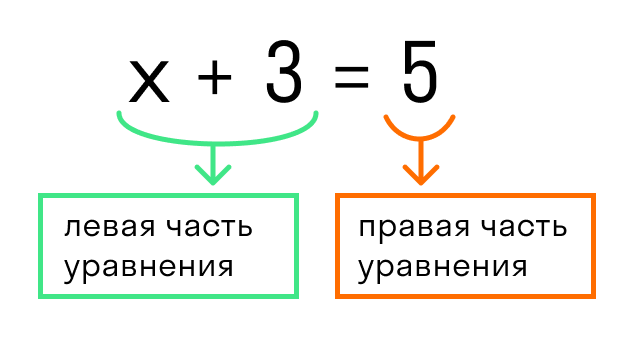
Для примера рассмотрим простейшее уравнение: x+3=5.

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

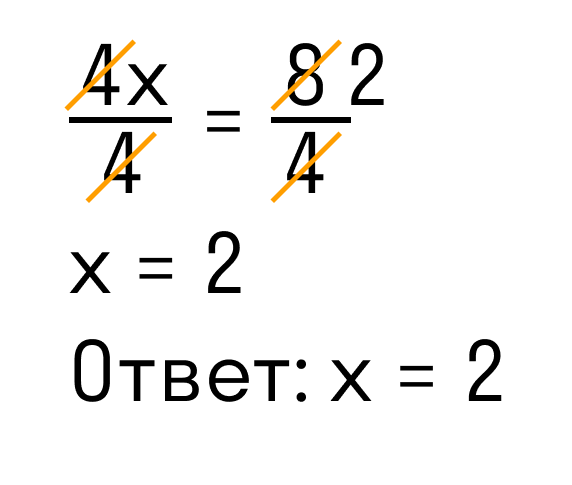
Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12

Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.

-4x = 12 | : (-4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Видео:Линейные уравнения в ОГЭ | Математика ОГЭ 2022 | УмскулСкачать

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

ЮПеренести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

6.5.1. Линейное уравнение с одной переменной

У очень многих школьников возникает вопрос — как решить уравнение с x. Что значит решить уравнение и как найти корень уравнения. Давайте рассмотрим основную схему решения обычного уравнения, называемого линейным, с одной переменной.

Видео:Алгебра 9 класс. 8 сентября. квадратные уравненияСкачать

Правила и определения

Основные правила и определения для линейного уравнения с одной переменной.

• Равенство с переменной называют уравнением.
• Решить уравнение – значит найти множество его корней. Уравнение может иметь один, два, несколько, множество корней или не иметь их вовсе.
• Каждое значение переменной, при котором данное уравнение превращается в верное равенство, называется корнем уравнения.
• Уравнения, имеющие одни и те же корни, называются равносильными уравнениями.
• Любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
• Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Примеры. Решить уравнение.

Уравнение 1

1. 1,5х-0,3х = -2-4. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
2. 1,2х = -6. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
3. х = -6 : 1,2. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.
4. х = -5. Делили по правилу деления десятичной дроби на десятичную дробь:
5. чтобы разделить число на десятичную дробь, нужно перенести запятые в делимом и делителе на столько цифр вправо, сколько их стоит после запятой в делителе, а затем выполнить деление на натуральное число: 6 : 1,2 = 60 : 12 = 5.

Ответ: 5.

Уравнение 2

3∙(2х-9) = 4∙(х-4).

1. 6х-27 = 4х-16. Раскрыли скобки, используя распределительный закон умножения относительно вычитания: чтобы разность двух чисел умножить на третье число, можно отдельно уменьшаемое и отдельно вычитаемое умножить на третье число, а затем из первого результата вычесть второй результат, т.е. (a-b) ∙ c = a ∙ c-b ∙ c.
2. 6х-4х = -16+27. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
3. 2х = 11. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
4. х = 11 : 2. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Ответ: 5,5.

Уравнение 3

1. 7х-3-2х = х-9. Раскрыли скобки по правилу раскрытия скобок, перед которыми стоит знак «-»: если перед скобками стоит знак «-», то убираем скобки, знак «-» и записываем слагаемые, стоявшие в скобках, с противоположными знаками.
2. 7х-2х-х = -9+3. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
3. 4х = -6. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
4. х = -6 : 4. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Ответ: -1,5.

Уравнение 4

1. 3 ∙ (х-5) = 7 ∙ 12 — 4 ∙ (2х-11). Умножили обе части равенства на 12 – наименьший общий знаменатель для знаменателей данных дробей.
2. 3х-15 = 84-8х+44. Раскрыли скобки, используя распределительный закон умножения относительно вычитания: чтобы разность двух чисел умножить на третье число, можно отдельно уменьшаемое и отдельно вычитаемое умножить на третье число, а затем из первого результата вычесть второй результат, т.е. (a-b) ∙ c = a ∙ c-b ∙ c.
3. 3х+8х = 84+44+15. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
4. 11х = 143. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
5. х = 143 : 11. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Ответ: 13.

Видео:Целое уравнение и его корни. Алгебра, 9 классСкачать

Уравнения для самостоятельного решения

Решить самостоятельно уравнения:

а) 3-2,6х = 5х+1,48;

б) 1,6 · (х+5) = 4 · (4,5-0,6х);

в) 9х- (6х+2,5) = — (х-5,5);

5а) 0,2; 5б) 2,5; 5в) 2; 5г) -1.

Видео:Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать

Важные выводы

Итак, для того, чтобы решить уравнение — надо определить его переменную, перенести неизвестную переменную в левую часть уравнения, а известные — в праву. При необходимости упростить левую и правую части и затем найти корень уравнения.

Видео:🔴 Найдите корень уравнения 2+9x=4x+3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

Задание №9 ОГЭ по математике

В девятом задании модуля алгебра ОГЭ по математике нам предлагают решить уравнения. Это могут быть как линейные уравнения, которые решаются переносом всех известных членов в одну сторону, а неизвестных (x) в другую, так и квадратные уравнения, которые в свою очередь могут быть полными и неполными. Судя по материалам ОГЭ и практике проведения экзамена, наиболее вероятным заданием может быть решение линейного или квадратного уравнения. Тем не менее мы рассмотрим задания по всей этой тематике. Сложность заданий как всегда возрастает от задания к заданию. Ответом в задании №9 является целое число или конечная десятичная дробь.

Теория к заданию №9

Ниже я привел теорию по решениям линейных и квадратных уравнений:

Схема решения, правила и алгоритм действий при решении линейного уравнения:

Схема решения, правила и порядок действий при решении квадратного уравнения:

В трех типовых вариантах я разобрал данные случаи – в первом варианте вы найдете подробные указания по решению линейных уравнений, во втором разобран пример решения неполного квадратного уравнения, а в третьем – решение полного квадратного уравнения с вычислением дискриминанта.

Найдите корень уравнения:

Данное уравнение представляет собой обыкновенное уравнение первой степени и решается переносом всех известных частей в правую часть, оставив x слева.

Для начала следует раскрыть скобки: 10x – 90 = 7

Затем переносим 90 в правую часть (не забываем поменять знак):

Затем делим обе части на 10:

pазбирался: Даниил Романович | обсудить разбор | оценить

Это неполное квадратное уравнение, в котором не обязательно вычислять дискриминант, а достаточно вынести x за скобку:

Произведение множителей тогда равно нулю, когда один из множителей равен нолю:

Так как в ответе просят указать наименьший корень, то это -4.

pазбирался: Даниил Романович | обсудить разбор | оценить

Уравнение является полным квадратным уравнением, поэтому классическим вариантом решения является вычисление дискриминанта. Но в данном случае можно заметить, что все множители кратны двум, поэтому можно все уравнение разделить на 2 для удобства вычисления:

Далее вычисляем дискриминант:

x = (- b — √D) / 2a = (5 — 3 )/ 2 •4 = 0,25

x = (- b + √D) / 2a = (5 + 3 )/ 2 •4 = 1

Так как нам нужно выбрать меньший из корней по условию, то выбираем 0,25

pазбирался: Даниил Романович | обсудить разбор | оценить

В данной задаче нам предстоит решить линейное уравнение. Подход к решению таких уравнений достаточно простой – всё, что известно переносим в правую часть, всё, что неизвестно – оставляем в левой. Далее выполняем необходимое арифметическое действие.

Переносим 9 в правую часть (не забываем про смену знака):

7х = 40 + 9, что эквивалентно

х в нашем случае – это неизвестный множитель, следовательно, чтобы его найти, делим произведение на известный множитель:

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите корень уравнения:

режде всего, исключим

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Далее решаем уравнение. Представляем число 2 в уравнении справа в виде дроби 2/1. Уравнение получает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Выполним умножение в левой части уравнения и раскроем скобки справа:

Поменяем местами левую и правую части уравнения, чтобы оно приняло привычный вид:

Переносим 12 из левой части в правую:

ОДЗ это значение не исключает, поэтому оно является искомым результатом.Ответ: -5,5

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите корень уравнения:

Обе части уравнения приводим к единому знаменателю 12: 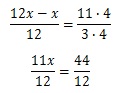Т.к. знаменатели в левой и правой частях уравнения одинаковы, не равны нулю и не содержат переменных, то их можно сократить (т.е. ими можно пренебречь). Тогда получаем: 11х=44 х=44:11 х=4

pазбирался: Даниил Романович | обсудить разбор | оценить

Имеем линейное уравнение:

Следовательно, начинаем решение с переноса слагаемых (с переменной влево, без переменной – вправо): 3х + 7х= – 5 – 2, не забывая изменять знак у слагаемых, которые переносим. Теперь приводим подобные в каждой части, получаем 10х= –7.

Находим неизвестный множитель делением произведения –7 на известный множитель 10, получаем –0,7.

Запись решения выглядит так:

pазбирался: Даниил Романович | обсудить разбор | оценить

🔥 Видео

Линейные уравнения. 9 класс, повторение.Скачать

ОГЭ для НОЛИКОВ, Уравнения N-9Скачать

Найди неизвестный корень. Повторение. Линейные уравнения. 9 класс.Скачать

Линейное уравнение с одной переменнойСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать

Решаем линейные уравнения на ОГЭ по математике 2022. Блок №1Скачать

Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Алгебра 7 Линейное уравнение с одной переменнойСкачать

Линейное уравнение с одной переменной. 6 класс.Скачать