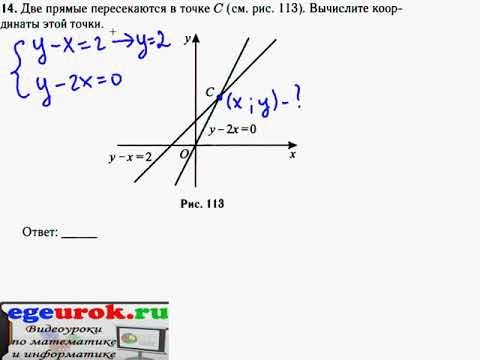
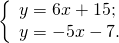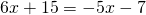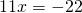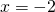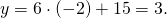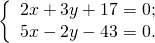Как найти координаты точки пересечения двух прямых если даны их уравнения (8 видео)

Координаты точки пересечения прямых

Две прямые на плоскости могут быть параллельными, пересекаться либо совпадать.

Чтобы найти координаты точки пересечения прямых, надо составить и решить систему уравнений, составленную из уравнений этих прямых.

Найти точку пересечения прямых заданных уравнениями:

2) 2x+3y+17=0; 5x-2y-43=0.

1) Составляем систему уравнений (здесь даны уравнения прямой с угловым коэффициентом):

Приравняем правые части уравнений:

Подставим x= -2 в уравнение первой прямой:

2) Составляем систему уравнений (здесь задано общее уравнение прямой):

Умножим 1-е уравнение системы на 2, а 2-е — на 3

Содержание

Координаты точки пересечения двух прямых — примеры нахождения
Точка пересечения двух прямых – определение
Нахождение координат точки пересечения двух прямых на плоскости
Нахождения координат точки пересечения двух прямых в пространстве
Координаты точки пересечения двух прямых — примеры нахождения.
Точка пересечения двух прямых – определение.
Нахождение координат точки пересечения двух прямых на плоскости.
Нахождение координат точки пересечения двух прямых в пространстве.
📽️ Видео

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Координаты точки пересечения двух прямых — примеры нахождения

Для того, чтобы решить геометрическую задачу методом координат, необходима точка пересечения, координаты которой используются при решении. Возникает ситуация, когда требуется искать координаты пересечения двух прямых на плоскости или определить координаты тех же прямых в пространстве. Данная статья рассматривает случаи нахождения координат точек, где пересекаются заданные прямые.

Видео:Найти координаты точки пересечения прямыхСкачать

Точка пересечения двух прямых – определение

Необходимо дать определение точкам пересечения двух прямых.

Раздел взаимного расположения прямых на плоскости показывает, что они могут совпадать , быть параллельными, пересекаться в одной общей точке или скрещивающимися. Две прямые, находящиеся в пространстве, называют пересекающимися, если они имеют одну общую точку.

Определение точки пересечения прямых звучит так:

Точка, в которой пересекаются две прямые, называют их точкой пересечения. Иначе говоря, что точка пересекающихся прямых и есть точка пересечения.

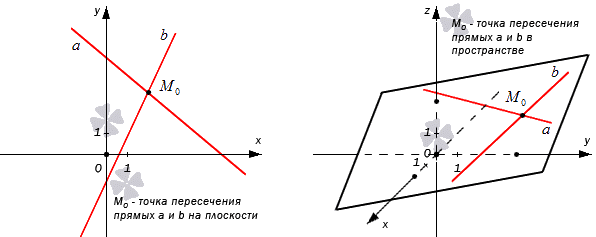
Рассмотрим на рисунке, приведенном ниже.

Видео:№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать

Нахождение координат точки пересечения двух прямых на плоскости

Перед нахождением координат точки пересечения двух прямых, необходимо рассмотреть предлагаемый ниже пример.

Если на плоскости имеется система координат О х у , то задаются две прямые a и b . Прямой a соответствует общее уравнение вида A 1 x + B 1 y + C 1 = 0 , для прямой b — A 2 x + B 2 y + C 2 = 0 . Тогда M 0 ( x 0 , y 0 ) является некоторой точкой плоскости необходимо выявить , будет ли точка М 0 являться точкой пересечения этих прямых.

Чтобы решить поставленную задачу, необходимо придерживаться определения. Тогда прямые должны пересекаться в точке, координаты которой являются решением заданных уравнений A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Значит, координаты точки пересечения подставляются во все заданные уравнения. Если они при подстановке дают верное тождество, тогда M 0 ( x 0 , y 0 ) считается их точкой пересечения.

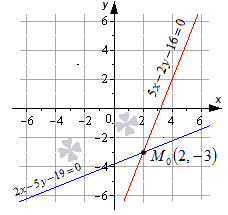
Даны две пересекающиеся прямые 5 x — 2 y — 16 = 0 и 2 x — 5 y — 19 = 0 . Будет ли точка М 0 с координатами ( 2 , — 3 ) являться точкой пересечения.

Чтобы пересечение прямых было действительным, необходимо, чтобы координаты точки М 0 удовлетворяли уравнениям прямых. Это проверяется при помощи их подстановки. Получаем, что

5 · 2 — 2 · ( — 3 ) — 16 = 0 ⇔ 0 = 0 2 · 2 — 5 · ( — 3 ) — 19 = 0 ⇔ 0 = 0

Оба равенства верные, значит М 0 ( 2 , — 3 ) является точкой пересечения заданных прямых.

Изобразим данное решение на координатной прямой рисунка, приведенного ниже.

Ответ: заданная точка с координатами ( 2 , — 3 ) будет являться точкой пересечения заданных прямых.

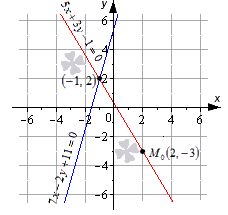
Пересекутся ли прямые 5 x + 3 y — 1 = 0 и 7 x — 2 y + 11 = 0 в точке M 0 ( 2 , — 3 ) ?

Для решения задачи необходимо подставить координаты точки во все уравнения. Получим, что

5 · 2 + 3 · ( — 3 ) — 1 = 0 ⇔ 0 = 0 7 · 2 — 2 · ( — 3 ) + 11 = 0 ⇔ 31 = 0

Второе равенство не является верным, значит, что заданная точка не принадлежит прямой 7 x — 2 y + 11 = 0 . Отсюда имеем, что точка М 0 не точка пересечения прямых.

Чертеж наглядно показывает, что М 0 — это не точка пересечения прямых. Они имеют общую точку с координатами ( — 1 , 2 ) .

Ответ: точка с координатами ( 2 , — 3 ) не является точкой пересечения заданных прямых.

Переходим к нахождению координат точек пересечения двух прямых при помощи заданных уравнений на плоскости.

Задаются две пересекающиеся прямые a и b уравнениями вида A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 , расположенных в О х у . При обозначении точки пересечения М 0 получим, что следует продолжить поиск координат по уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 .

Из определения очевидно, что М 0 является общей точкой пересечения прямых. В этом случае ее координаты должны удовлетворять уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Иными словами это и есть решение полученной системы A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 y + C 2 = 0 .

Значит, для нахождения координат точки пересечения , необходимо все уравнения добавить в систему и решить ее.

Заданы две прямые x — 9 y + 14 = 0 и 5 x — 2 y — 16 = 0 на плоскости. необходимо найти их пересечение.

Данные по условию уравнения необходимо собрать в систему, после чего получим x — 9 y + 14 = 0 5 x — 2 y — 16 = 0 . Чтобы решить его, разрешается первое уравнение относительно x , подставляется выражение во второе:

x — 9 y + 14 = 0 5 x — 2 y — 16 = 0 ⇔ x = 9 y — 14 5 x — 2 y — 16 = 0 ⇔ ⇔ x = 9 y — 14 5 · 9 y — 14 — 2 y — 16 = 0 ⇔ x = 9 y — 14 43 y — 86 = 0 ⇔ ⇔ x = 9 y — 14 y = 2 ⇔ x = 9 · 2 — 14 y = 2 ⇔ x = 4 y = 2

Получившиеся числа являются координатами, которые необходимо было найти.

Ответ: M 0 ( 4 , 2 ) является точкой пересечения прямых x — 9 y + 14 = 0 и 5 x — 2 y — 16 = 0 .

Поиск координат сводится к решению системы линейных уравнений. Если по условию дан другой вид уравнения, тогда следует привести его к нормальному виду.

Определить координаты точек пересечения прямых x — 5 = y — 4 — 3 и x = 4 + 9 · λ y = 2 + λ , λ ∈ R .

Для начала необходимо привести уравнения к общему виду. Тогда получаем, что x = 4 + 9 · λ y = 2 + λ , λ ∈ R преобразуется таким образом:

x = 4 + 9 · λ y = 2 + λ ⇔ λ = x — 4 9 λ = y — 2 1 ⇔ x — 4 9 = y — 2 1 ⇔ ⇔ 1 · ( x — 4 ) = 9 · ( y — 2 ) ⇔ x — 9 y + 14 = 0

После чего беремся за уравнение канонического вида x — 5 = y — 4 — 3 и преобразуем. Получаем, что

x — 5 = y — 4 — 3 ⇔ — 3 · x = — 5 · y — 4 ⇔ 3 x — 5 y + 20 = 0

Отсюда имеем, что координаты – это точка пересечения

x — 9 y + 14 = 0 3 x — 5 y + 20 = 0 ⇔ x — 9 y = — 14 3 x — 5 y = — 20

Применим метод Крамера для нахождения координат:

∆ = 1 — 9 3 — 5 = 1 · ( — 5 ) — ( — 9 ) · 3 = 22 ∆ x = — 14 — 9 — 20 — 5 = — 14 · ( — 5 ) — ( — 9 ) · ( — 20 ) = — 110 ⇒ x = ∆ x ∆ = — 110 22 = — 5 ∆ y = 1 — 14 3 — 20 = 1 · ( — 20 ) — ( — 14 ) · 3 = 22 ⇒ y = ∆ y ∆ = 22 22 = 1

Ответ: M 0 ( — 5 , 1 ) .

Имеется еще способ для нахождения координат точки пересечения прямых, находящихся на плоскости. Он применим, когда одна из прямых задается параметрическими уравнениями, имеющими вид x = x 1 + a x · λ y = y 1 + a y · λ , λ ∈ R . Тогда вместо значения x подставляется x = x 1 + a x · λ и y = y 1 + a y · λ , где получим λ = λ 0 , соответствующее точке пересечения, имеющей координаты x 1 + a x · λ 0 , y 1 + a y · λ 0 .

Определить координаты точки пересечения прямой x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x — 5 = y — 4 — 3 .

Необходимо выполнить подстановку в x — 5 = y — 4 — 3 выражением x = 4 + 9 · λ , y = 2 + λ , тогда получим:

4 + 9 · λ — 5 = 2 + λ — 4 — 3

При решении получаем, что λ = — 1 . Отсюда следует, что имеется точка пересечения между прямыми x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x — 5 = y — 4 — 3 . Для вычисления координат необходимо подставить выражение λ = — 1 в параметрическое уравнение. Тогда получаем, что x = 4 + 9 · ( — 1 ) y = 2 + ( — 1 ) ⇔ x = — 5 y = 1 .

Ответ: M 0 ( — 5 , 1 ) .

Для полного понимания темы, необходимо знать некоторые нюансы.

Предварительно необходимо понять расположение прямых. При их пересечении мы найдем координаты, в других случаях решения существовать не будет. Чтобы не делать эту проверку, можно составлять систему вида A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 + C 2 = 0 При наличии решения делаем вывод о том, что прямые пересекаются. Если решение отсутствует, то они параллельны. Когда система имеет бесконечное множество решений, тогда говорят, что они совпадают.

Даны прямые x 3 + y — 4 = 1 и y = 4 3 x — 4 . Определить, имеют ли они общую точку.

Упрощая заданные уравнения, получаем 1 3 x — 1 4 y — 1 = 0 и 4 3 x — y — 4 = 0 .

Следует собрать уравнения в систему для последующего решения:

1 3 x — 1 4 y — 1 = 0 1 3 x — y — 4 = 0 ⇔ 1 3 x — 1 4 y = 1 4 3 x — y = 4

Отсюда видно, что уравнения выражаются друг через друга, тогда получим бесконечное множество решений. Тогда уравнения x 3 + y — 4 = 1 и y = 4 3 x — 4 определяют одну и ту же прямую. Поэтому нет точек пересечения.

Ответ: заданные уравнения определяют одну и ту же прямую.

Найти координаты точки пересекающихся прямых 2 x + ( 2 — 3 ) y + 7 = 0 и 2 3 + 2 x — 7 y — 1 = 0 .

По условию возможно такое, прямые не будут пересекаться. Необходимо составить систему уравнений и решать. Для решения необходимо использовать метод Гаусса, так как с его помощью есть возможность проверить уравнение на совместимость. Получаем систему вида:

2 x + ( 2 — 3 ) y + 7 = 0 2 ( 3 + 2 ) x — 7 y — 1 = 0 ⇔ 2 x + ( 2 — 3 ) y = — 7 2 ( 3 + 2 ) x — 7 y = 1 ⇔ ⇔ 2 x + 2 — 3 y = — 7 2 ( 3 + 2 ) x — 7 y + ( 2 x + ( 2 — 3 ) y ) · ( — ( 3 + 2 ) ) = 1 + — 7 · ( — ( 3 + 2 ) ) ⇔ ⇔ 2 x + ( 2 — 3 ) y = — 7 0 = 22 — 7 2

Получили неверное равенство, значит система не имеет решений. Делаем вывод, что прямые являются параллельными. Точек пересечения нет.

Второй способ решения.

Для начала нужно определить наличие пересечения прямых.

n 1 → = ( 2 , 2 — 3 ) является нормальным вектором прямой 2 x + ( 2 — 3 ) y + 7 = 0 , тогда вектор n 2 → = ( 2 ( 3 + 2 ) , — 7 — нормальный вектор для прямой 2 3 + 2 x — 7 y — 1 = 0 .

Необходимо выполнить проверку коллинеарности векторов n 1 → = ( 2 , 2 — 3 ) и n 2 → = ( 2 ( 3 + 2 ) , — 7 ) . Получим равенство вида 2 2 ( 3 + 2 ) = 2 — 3 — 7 . Оно верное, потому как 2 2 3 + 2 — 2 — 3 — 7 = 7 + 2 — 3 ( 3 + 2 ) 7 ( 3 + 2 ) = 7 — 7 7 ( 3 + 2 ) = 0 . Отсюда следует, что векторы коллинеарны. Значит, прямые являются параллельными и не имеют точек пересечения.

Ответ: точек пересечения нет, прямые параллельны.

Найти координаты пересечения заданных прямых 2 x — 1 = 0 и y = 5 4 x — 2 .

Для решения составляем систему уравнений. Получаем

2 x — 1 = 0 5 4 x — y — 2 = 0 ⇔ 2 x = 1 5 4 x — y = 2

Найдем определитель основной матрицы. Для этого 2 0 5 4 — 1 = 2 · ( — 1 ) — 0 · 5 4 = — 2 . Так как он не равен нулю, система имеет 1 решение. Отсюда следует, что прямые пересекаются. Решим систему для нахождения координат точек пересечения:

2 x = 1 5 4 x — y = 2 ⇔ x = 1 2 4 5 x — y = 2 ⇔ x = 1 2 5 4 · 1 2 — y = 2 ⇔ x = 1 2 y = — 11 8

Получили, что точка пересечения заданных прямых имеет координаты M 0 ( 1 2 , — 11 8 ) .

Ответ: M 0 ( 1 2 , — 11 8 ) .

Видео:Не выполняя построения графиков, найдите координаты точки пересечения прямых. Алгебра 7 класс.Скачать

Нахождения координат точки пересечения двух прямых в пространстве

Таким же образом находятся точки пересечения прямых пространства.

Когда заданы прямые a и b в координатной плоскости О х у z уравнениями пересекающихся плоскостей, то имеется прямая a , которая может быть определена при помощи заданной системы A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 1 = 0 а прямая b — A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 .

Когда точка М 0 является точкой пересечения прямых, тогда ее координаты должны быть решениями обоих уравнений. Получим линейные уравнения в системе:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0

Рассмотрим подобные задания на примерах.

Найти координаты точки пересечения заданных прямых x — 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x — 2 z — 4 = 0

Составляем систему x — 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x — 2 z — 4 = 0 и решим ее. Чтобы найти координаты, необходимо решать через матрицу. Тогда получим основную матрицу вида A = 1 0 0 0 1 2 3 2 0 4 0 — 2 и расширенную T = 1 0 0 1 0 1 2 — 3 4 0 — 2 4 . Определяем ранг матрицы по Гауссу.

1 = 1 ≠ 0 , 1 0 0 1 = 1 ≠ 0 , 1 0 0 0 1 2 3 2 0 = — 4 ≠ 0 , 1 0 0 1 0 1 2 — 3 3 2 0 — 3 4 0 — 2 4 = 0

Отсюда следует, что ранг расширенной матрицы имеет значение 3 . Тогда система уравнений x — 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x — 27 — 4 = 0 в результате дает только одно решение.

Базисный минор имеет определитель 1 0 0 0 1 2 3 2 0 = — 4 ≠ 0 , тогда последнее уравнение не подходит. Получим, что x — 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x — 2 z — 4 = 0 ⇔ x = 1 y + 2 z = — 3 3 x + 2 y — 3 . Решение системы x = 1 y + 2 z = — 3 3 x + 2 y = — 3 ⇔ x = 1 y + 2 z = — 3 3 · 1 + 2 y = — 3 ⇔ x = 1 y + 2 z = — 3 y = — 3 ⇔ ⇔ x = 1 — 3 + 2 z = — 3 y = — 3 ⇔ x = 1 z = 0 y = — 3 .

Значит, имеем, что точка пересечения x — 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x — 2 z — 4 = 0 имеет координаты ( 1 , — 3 , 0 ) .

Ответ: ( 1 , — 3 , 0 ) .

Система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 имеет только одно решение. Значит, прямые a и b пересекаются.

В остальных случаях уравнение не имеет решения, то есть и общих точек тоже. То есть невозможно найти точку с координатами, так как ее нет.

Поэтому система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 решается методом Гаусса. При ее несовместимости прямые не являются пересекающимися. Если решений бесконечное множество, то они совпадают.

Можно произвести решение при помощи вычисления основного и расширенного ранга матрицы, после чего применить теорему Кронекера-Капелли. Получим одно, множество или полное отсутствие решений.

Заданы уравнения прямых x + 2 y — 3 z — 4 = 0 2 x — y + 5 = 0 и x — 3 z = 0 3 x — 2 y + 2 z — 1 = 0 . Найти точку пересечения.

Для начала составим систему уравнений. Получим, что x + 2 y — 3 z — 4 = 0 2 x — y + 5 = 0 x — 3 z = 0 3 x — 2 y + 2 z — 1 = 0 . решаем ее методом Гаусса:

1 2 — 3 4 2 — 1 0 — 5 1 0 — 3 0 3 — 2 2 1

1 2 — 3 4 0 — 5 6 — 13 0 — 2 0 — 4 0 — 8 11 — 11

1 2 — 3 4 0 — 5 6 — 13 0 0 — 12 5 6 5 0 0 7 5 — 159 5

1 2 — 3 4 0 — 5 6 — 13 0 0 — 12 5 6 5 0 0 0 311 10

Очевидно, что система не имеет решений, значит прямые не пересекаются. Точки пересечения нет.

Ответ: нет точки пересечения.

Если прямые заданы при помощи кононических или параметрических уравнений, нужно привести к виду уравнений пересекающихся плоскостей, после чего найти координаты.

Заданы две прямые x = — 3 — λ y = — 3 · λ z = — 2 + 3 · λ , λ ∈ R и x 2 = y — 3 0 = z 5 в О х у z . Найти точку пересечения.

Задаем прямые уравнениями двух пересекающихся плоскостей. Получаем, что

x = — 3 — λ y = — 3 · λ z = — 2 + 3 · λ ⇔ λ = x + 3 — 1 λ = y — 3 λ = z + 2 3 ⇔ x + 3 — 1 = y — 3 = z + 2 3 ⇔ ⇔ x + 3 — 1 = y — 3 x + 3 — 1 = z + 2 3 ⇔ 3 x — y + 9 = 0 3 x + z + 11 = 0 x 2 = y — 3 0 = z 5 ⇔ y — 3 = 0 x 2 = z 5 ⇔ y — 3 = 0 5 x — 2 z = 0

Находим координаты 3 x — y + 9 = 0 3 x + z + 11 = 0 y — 3 = 0 5 x — 2 z = 0 , для этого посчитаем ранги матрицы. Ранг матрицы равен 3 , а базисный минор 3 — 1 0 3 0 1 0 1 0 = — 3 ≠ 0 , значит, что из системы необходимо исключить последнее уравнение. Получаем, что

3 x — y + 9 = 0 3 x + z + 11 = 0 y — 3 = 0 5 x — 2 z = 0 ⇔ 3 x — y + 9 = 0 3 x + z + 11 = 0 y — 3 = 0

Решим систему методом Крамер. Получаем, что x = — 2 y = 3 z = — 5 . Отсюда получаем, что пересечение заданных прямых дает точку с координатами ( — 2 , 3 , — 5 ) .

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Координаты точки пересечения двух прямых — примеры нахождения.

При решении некоторых геометрических задач методом координат приходится находить координаты точки пересечения прямых. Наиболее часто приходится искать координаты точки пересечения двух прямых на плоскости, однако иногда возникает необходимость в определении координат точки пересечения двух прямых в пространстве. В этой статье мы как раз разберемся с нахождением координат точки, в которой пересекаются две прямые.

Навигация по странице.

Видео:Выделение ФУНКЦИИ из уравнений прямых. Найти точку пересечения прямых, заданных уравнениямиСкачать

Точка пересечения двух прямых – определение.

Давайте для начала дадим определение точки пересечения двух прямых.

В разделе взаимное расположение прямых на плоскости показано, что две прямые на плоскости могут либо совпадать (при этом они имеют бесконечно много общих точек), либо быть параллельными (при этом две прямые не имеют общих точек), либо пересекаться, имея одну общую точку. Вариантов взаимного расположения двух прямых в пространстве больше – они могут совпадать (иметь бесконечно много общих точек), могут быть параллельными (то есть, лежать в одной плоскости и не пересекаться), могут быть скрещивающимися (не лежащими в одной плоскости), а также могут иметь одну общую точку, то есть, пересекаться. Итак, две прямые и на плоскости и в пространстве называются пересекающимися, если они имеют одну общую точку.

Из определения пересекающихся прямых следует определение точки пересечения прямых: точка, в которой пересекаются две прямые, называется точкой пересечения этих прямых. Другими словами, единственная общая точка двух пересекающихся прямых есть точка пересечения этих прямых.

Приведем для наглядности графическую иллюстрацию точки пересечения двух прямых на плоскости и в пространстве.

Видео:Составляем уравнение прямой по точкамСкачать

Нахождение координат точки пересечения двух прямых на плоскости.

Прежде чем находить координаты точки пересечения двух прямых на плоскости по их известным уравнениям, рассмотрим вспомогательную задачу.

Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy и заданы две пересекающиеся прямые a и b . Будем считать, что прямой a соответствует общее уравнение прямой вида , а прямой b – вида . Пусть – некоторая точка плоскости, и требуется выяснить, является ли точка М₀ точкой пересечения заданных прямых.

Решим поставленную задачу.

Если M₀ является точкой пересечения прямых a и b , то по определению она принадлежит и прямой a и прямой b , то есть, ее координаты должны удовлетворять одновременно и уравнению и уравнению . Следовательно, нам нужно подставить координаты точки М₀ в уравнения заданных прямых и посмотреть, получаются ли при этом два верных равенства. Если координаты точки М₀ удовлетворяют обоим уравнениям и , то – точка пересечения прямых a и b , в противном случае М₀ не является точкой пересечения прямых.

Является ли точка М₀ с координатами (2, -3) точкой пересечения прямых 5x-2y-16=0 и 2x-5y-19=0 ?

Если М₀ действительно точка пересечения заданных прямых, то ее координаты удовлетворяют уравнениям прямых. Проверим это, подставив координаты точки М₀ в заданные уравнения:

Получили два верных равенства, следовательно, М₀ (2, -3) — точка пересечения прямых 5x-2y-16=0 и 2x-5y-19=0 .

Для наглядности приведем чертеж, на котором изображены прямые и видны координаты точки их пересечения.

да, точка М₀ (2, -3) является точкой пересечения прямых 5x-2y-16=0 и 2x-5y-19=0 .

Пересекаются ли прямые 5x+3y-1=0 и 7x-2y+11=0 в точке M₀ (2, -3) ?

Подставим координаты точки М₀ в уравнения прямых, этим действием будем осуществлена проверка принадлежности точки М₀ обеим прямым одновременно:

Так как второе уравнение при подстановке в него координат точки М₀ не обратилось в верное равенство, то точка М₀ не принадлежит прямой 7x-2y+11=0 . Из этого факта можно сделать вывод о том, что точка М₀ не является точкой пересечения заданных прямых.

На чертеже также хорошо видно, что точка М₀ не является точкой пересечения прямых 5x+3y-1=0 и 7x-2y+11=0 . Очевидно, заданные прямые пересекаются в точке с координатами (-1, 2) .

М₀ (2, -3) не является точкой пересечения прямых 5x+3y-1=0 и 7x-2y+11=0 .

Теперь можно переходить к задаче нахождения координат точки пересечения двух прямых по заданным уравнениям прямых на плоскости.

Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy и заданы две пересекающиеся прямые a и b уравнениями и соответственно. Обозначим точку пересечения заданных прямых как М₀ и решим следующую задачу: найти координаты точки пересечения двух прямых a и b по известным уравнениям этих прямых и .

Точка M₀ принадлежит каждой из пересекающихся прямых a и b по определению. Тогда координаты точки пересечения прямых a и b удовлетворяют одновременно и уравнению и уравнению . Следовательно, координаты точки пересечения двух прямых a и b являются решением системы уравнений (смотрите статью решение систем линейных алгебраических уравнений).

Таким образом, чтобы найти координаты точки пересечения двух прямых, определенных на плоскости общими уравнениями, нужно решить систему, составленную из уравнений заданных прямых.

Рассмотрим решение примера.

Найдите точку пересечения двух прямых, определенных в прямоугольной системе координат на плоскости уравнениями x-9y+14=0 и 5x-2y-16=0 .

Нам даны два общих уравнения прямых, составим из них систему: . Решения полученной системы уравнений легко находятся, если разрешить ее первое уравнение относительно переменной x и подставить это выражение во второе уравнение:

Найденное решение системы уравнений дает нам искомые координаты точки пересечения двух прямых.

M₀ (4, 2) – точка пересечения прямых x-9y+14=0 и 5x-2y-16=0 .

Итак, нахождение координат точки пересечения двух прямых, определенных общими уравнениями на плоскости, сводится к решению системы из двух линейных уравнений с двумя неизвестными переменными. А как же быть, если прямые на плоскости заданы не общими уравнениями, а уравнениями другого вида (смотрите виды уравнения прямой на плоскости)? В этих случаях можно сначала привести уравнения прямых к общему виду, а уже после этого находить координаты точки пересечения.

Определите координаты точки пересечения прямых и .

Перед нахождением координат точки пересечения заданных прямых приведем их уравнения к общему виду. Переход от параметрических уравнений прямой к общему уравнению этой прямой выглядит следующим образом:

Теперь проведем необходимые действия с каноническим уравнением прямой :

Таким образом, искомые координаты точки пересечения прямых являются решением системы уравнений вида . Используем для ее решения метод Крамера:

Существует еще один способ нахождения координат точки пересечения двух прямых на плоскости. Его удобно применять, когда одна из прямых задана параметрическими уравнениями вида , а другая – уравнением прямой иного вида. В этом случае в другое уравнение вместо переменных x и y можно подставить выражения и , откуда можно будет получить значение , которое соответствует точке пересечения заданных прямых. При этом точка пересечения прямых имеет координаты .

Найдем координаты точки пересечения прямых из предыдущего примера этим способом.

Определите координаты точки пересечения прямых и .

Подставим в уравнение прямой выражения :

Решив полученное уравнение, получаем . Это значение соответствует общей точке прямых и . Вычисляем координаты точки пересечения, подставив в параметрические уравнения прямой:
.

Для полноты картины следует обговорить еще один момент.

Перед нахождением координат точки пересечения двух прямых на плоскости полезно убедиться в том, что заданные прямые действительно пересекаются. Если выяснится, что исходные прямые совпадают или параллельны, то о нахождении координат точки пересечения таких прямых не может быть и речи.

Можно, конечно, обойтись и без такой проверки, а сразу составить систему уравнений вида и решить ее. Если система уравнений имеет единственное решение, то оно дает координаты точки, в которой исходные прямые пересекаются. Если система уравнений решений не имеет, то можно делать вывод о параллельности исходных прямых (так как не существует такой пары действительных чисел x и y , которая бы удовлетворяла одновременно обоим уравнениям заданных прямых). Из наличия бесконечного множества решений системы уравнений следует, что исходные прямые имеют бесконечно много общих точек, то есть, совпадают.

Рассмотрим примеры, подходящие под эти ситуации.

Выясните, пересекаются ли прямые и , и если пересекаются, то найдите координаты точки пересечения.

Заданным уравнениям прямых соответствуют уравнения и . Решим систему, составленную из этих уравнений .

Очевидно, что уравнения системы линейно выражаются друг через друга (второе уравнение системы получается из первого умножением обеих его частей на 4 ), следовательно, система уравнений имеет бесконечное множество решений. Таким образом, уравнения и определяют одну и ту же прямую, и мы не можем говорить о нахождении координат точки пересечения этих прямых.

уравнения и определяют в прямоугольной системе координат Oxy одну и ту же прямую, поэтому мы не можем говорить о нахождении координат точки пересечения.

Найдите координаты точки пересечения прямых и , если это возможно.

Условие задачи допускает, что прямые могут быть не пересекающимися. Составим систему из данных уравнений. Применим для ее решения метод Гаусса, так как он позволяет установить совместность или несовместность системы уравнений, а в случае ее совместности найти решение:

Последнее уравнение системы после прямого хода метода Гаусса обратилось в неверное равенство, следовательно, система уравнений не имеет решений. Отсюда можно сделать вывод, что исходные прямые параллельны, и мы не можем говорить о нахождении координат точки пересечения этих прямых.

Второй способ решения.

Давайте выясним, пересекаются ли заданные прямые.

— нормальный вектор прямой , а вектор является нормальным вектором прямой . Проверим выполнение условия коллинеарности векторов и : равенство верно, так как , следовательно, нормальные векторы заданных прямых коллинеарны. Тогда, эти прямые параллельны или совпадают. Таким образом, мы не можем найти координаты точки пересечения исходных прямых.

координаты точки пересечения заданных прямых найти невозможно, так как эти прямые параллельны.

Найдите координаты точки пересечения прямых 2x-1=0 и , если они пересекаются.

Составим систему из уравнений, которые являются общими уравнениями заданных прямых: . Определитель основной матрицы этой системы уравнений отличен от нуля , поэтому система уравнений имеет единственное решение, что свидетельствует о пересечении заданных прямых.

Для нахождения координат точки пересечения прямых нам нужно решить систему:

Полученное решение дает нам координаты точки пересечения прямых, то есть, — точка пересечения прямых 2x-1=0 и .

Видео:Нахождение координат точек пересечения графика функции с осями координатСкачать

Нахождение координат точки пересечения двух прямых в пространстве.

Координаты точки пересечения двух прямых в трехмерном пространстве находятся аналогично.

Пусть пересекающиеся прямые a и b заданы в прямоугольной системе координат Oxyz уравнениями двух пересекающихся плоскостей, то есть, прямая a определяется системой вида , а прямая b — . Пусть М₀ – точка пересечения прямых a и b . Тогда точка М₀ по определению принадлежит и прямой a и прямой b , следовательно, ее координаты удовлетворяют уравнениям обеих прямых. Таким образом, координаты точки пересечения прямых a и b представляют собой решение системы линейных уравнений вида . Здесь нам пригодится информация из раздела решение систем линейных уравнений, в которых число уравнений не совпадает с числом неизвестных переменных.

Рассмотрим решения примеров.

Найдите координаты точки пересечения двух прямых, заданных в пространстве уравнениями и .

Составим систему уравнений из уравнений заданных прямых: . Решение этой системы даст нам искомые координаты точки пересечения прямых в пространстве. Найдем решение записанной системы уравнений.

Основная матрица системы имеет вид , а расширенная — .

Определим ранг матрицы А и ранг матрицы T . Используем метод окаймляющих миноров, при этом не будем подробно описывать вычисление определителей (при необходимости обращайтесь к статье вычисление определителя матрицы):

Таким образом, ранг основной матрицы равен рангу расширенной матрицы и равен трем.

Следовательно, система уравнений имеет единственное решение.

Базисным минором примем определитель , поэтому из системы уравнений следует исключить последнее уравнение, так как оно не участвует в образовании базисного минора. Итак,

Решение полученной системы легко находится:

Таким образом, точка пересечения прямых и имеет координаты (1, -3, 0) .

Следует отметить, что система уравнений имеет единственное решение тогда и только тогда, когда прямые a и b пересекаются. Если же прямые а и b параллельные или скрещивающиеся, то последняя система уравнений решений не имеет, так как в этом случае прямые не имеют общих точек. Если прямые a и b совпадают, то они имеют бесконечное множество общих точек, следовательно, указанная система уравнений имеет бесконечное множество решений. Однако в этих случаях мы не можем говорить о нахождении координат точки пересечения прямых, так как прямые не являются пересекающимися.

Таким образом, если мы заранее не знаем, пересекаются заданные прямые a и b или нет, то разумно составить систему уравнений вида и решить ее методом Гаусса. Если получим единственное решение, то оно будет соответствовать координатам точки пересечения прямых a и b . Если система окажется несовместной, то прямые a и b не пересекаются. Если же система будет иметь бесконечное множество решений, то прямые a и b совпадают.

Можно обойтись и без использования метода Гаусса. Как вариант, можно вычислить ранги основной и расширенной матриц этой системы, и на основании полученных данных и теоремы Кронекера-Капелли сделать вывод или о существовании единственного решения, или о существовании множества решений, или об отсутствии решений. Это дело вкуса.

Если прямые и пересекаются, то определите координаты точки пересечения.

Составим систему из заданных уравнений: . Решим ее методом Гаусса в матричной форме:

Стало видно, что система уравнений не имеет решений, следовательно, заданные прямые не пересекаются, и не может быть и речи о поиске координат точки пересечения этих прямых.

мы не можем найти координаты точки пересечения заданных прямых, так как эти прямые не пересекаются.

Когда пересекающиеся прямые заданы каноническими уравнениями прямой в пространстве или параметрическими уравнениями прямой в пространстве, то следует сначала получить их уравнения в виде двух пересекающихся плоскостей, а уже после этого находить координаты точки пересечения.

Две пересекающиеся прямые заданы в прямоугольной системе координат Oxyz уравнениями и . Найдите координаты точки пересечения этих прямых.

Зададим исходные прямые уравнениями двух пересекающихся плоскостей:

Для нахождения координат точки пересечения прямых осталось решить систему уравнений . Ранг основной матрицы этой системы равен рангу расширенной матрицы и равен трем (рекомендуем проверить этот факт). В качестве базисного минора примем , следовательно, из системы можно исключить последнее уравнение . Решив полученную систему любым методом (например методом Крамера) получаем решение . Таким образом, точка пересечения прямых и имеет координаты (-2, 3, -5) .