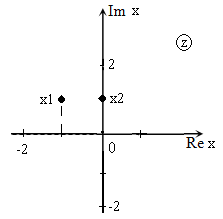Как найти комплексные корни квадратного уравнения и изобразить их на комплексной плоскости (8 видео)

Как найти комплексные корни квадратного уравнения и изобразить их на комплексной плоскости

. Вы вводите его по ссылке решение уравнений онлайн , указываете, что i — это комплексная единица (после того как ввели уравнение и нажали кнопку «решить»), нажимаете кнопку под формой «Обновить» и получаете ответ как здесь. Если в ответе присутствуют корни из комплексных чисел, то можно воспользоваться калькулятором по упрощению комлексных чисел по ссылке

Содержание

Числа. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.
Как извлечь корень из произвольного комплексного числа?
Квадратное уравнение с комплексными корнями
Готовые работы на аналогичную тему
📸 Видео

Видео:Комплексные корни квадратного уравненияСкачать

Числа. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.

Рассматривать будем на таком примере:

Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:

Выполним проверку того, что эти корни и права оказываются решением уравнения:

Что и требовалось доказать.

Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: .

Такие корни являются сопряженными комплексными корнями.

Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:

, ,

В каждом случае получаем 2 сопряженных комплексных корня.

Решим квадратное уравнение .

Первым шагом определим дискриминант уравнения:

В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:

Как известно из формул дискриминанта у нас образуется 2 корня:

– сопряженные комплексные корни

Т.о., у уравнения есть 2 сопряженных комплексных корня:

Теперь можно решить любое квадратное уравнение!

У любого уравнения с многочленом n-ой степени есть ровно n корней, некоторые из них могут быть комплексными.

Видео:Изобразить область на комплексной плоскостиСкачать

Как извлечь корень из произвольного комплексного числа?

Рассмотрим уравнение z n = w, либо, записав в другом виде: . Здесь n может принимать всякое натуральное значение, которое больше 1-цы.

В частности, при n = 2 получаем квадратный корень .

У уравнения типа есть ровно n корней z₀, z₁, z₂, … z_n_-1, которые можно вычислить с помощью формулы:

где – это модуль комплексного числа w,

φ – его аргумент,

а параметр k принимает значения: .

Найдем корни уравнения: .

Перепишем уравнение как: .

В этом примере , , поэтому у уравнения будет 2 корня: z₀ и z₁. Детализируем общую формулу:

, .

Далее найдем модуль и аргумент комплексного числа :

Число w находится в 1-ой четверти, значит:

Помним, что определяя тригонометрическую форму комплексного числа лучше делать чертеж.

Детализируем еще немного общую формулу:

, .

Так подобно расписывать не обязательно. Здесь мы это сделали, что бы было ясно откуда что образовалось.

Подставляем в формулу значение k = 0 и получаем 1-й корень:

Подставляем в формулу значение k = 1 и получаем 2-й корень:

Ответ: ,

Если необходимо, корни, которые мы получили можно перевести обратно в алгебраическую форму.

Часто вычисленные корни нужно изобразить геометрически:

Как выполнить чертеж?

Для начала на калькуляторе вычисляем, чему равен модуль корней и чертим с помощью циркуля окружность этого радиуса. Все корни будем откладывать на данной окружности.

Далее берем аргумент 1-го корня и вычисляем, чему равен угол в градусах:

Отмеряем транспортиром 45° и ставим на чертеже точку z₀.

Берем аргумент 2-го корня и переводим его тоже в градусы: . Отмеряем транспортиром 165° и ставим на чертеже точку z₁.

По этому же алгоритму ставим точку z₂.

Видно, что корни располагаются геометрически правильно с интервалом между радиус-векторами. Чертеж обязательно делать при помощи транспортира.

Видео:Комплексные корни квадратных уравнений. 11 класс.Скачать

Квадратное уравнение с комплексными корнями

Вы будете перенаправлены на Автор24

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Двучленным называется уравнение вида $x^ =A$.

Рассмотрим три случая:

Решить уравнение: $x^ =8$.

Так как $A>0$, то $x_ =sqrt[] cdot left(cos frac +icdot sin frac right),, , , k=0. 2$.

При $k=0$ получаем $x_ =sqrt[] cdot left(cos 0+icdot sin 0right)=sqrt[] =2$.

При $k=1$ получаем

[x_ =sqrt[] cdot left(cos frac +icdot sin frac right)=sqrt[] cdot (-frac +frac <sqrt> cdot i)=2cdot (-frac +frac <sqrt> cdot i)=-1+sqrt cdot i.]

При $k=2$ получаем

[x_ =sqrt[] cdot left(cos frac +icdot sin frac right)=sqrt[] cdot (-frac -frac <sqrt> cdot i)=2cdot (-frac -frac <sqrt> cdot i)=-1-sqrt cdot i.]

Решить уравнение: $x^ =1+i$.

Готовые работы на аналогичную тему

Так как $A$ — комплексное число, то

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа:

[varphi =arg z=arctgfrac =arctg1=frac ]

Подставим полученные значения и получим:

Уравнение перепишем в виде:

При $k=0$ получаем $x_ =sqrt[] <sqrt> cdot left(cos frac +icdot sin frac right)=sqrt[] <sqrt> cdot left(cos frac +icdot sin frac right)=sqrt[] cdot left(cos frac +icdot sin frac right)$.

При $k=1$ получаем

При $k=2$ получаем

Квадратным называется уравнение вида $ax^ +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^ -4ac$, при этом

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

Решить уравнение $x^ +2x+5=0$ и изобразить корни на плоскости.

[D=2^ -4cdot 1cdot 5=4-20=-16.]

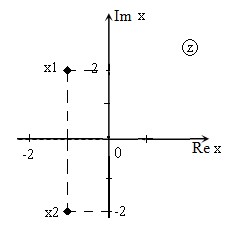
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Комплексное число вида $overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Известно, что если $x_ $ являются корнями квадратного уравнения $ax^ +bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ )(x-x_ )=0$. В общем случае $x_ $ являются комплексными корнями.

Зная корни уравнения $x_ =1pm 2i$, записать исходное уравнение.

Запишем уравнение следующим образом:

[x^ -(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0] [x^ -x+2icdot x-x-2icdot x+1-4i^ =0] [x^ -2x+1+4=0] [x^ -2x+5=0]

Следовательно, $x^ -2x+5=0$ — искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Решить уравнение: $z^ +(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.

Так как $D>0$, уравнение имеет два корня:

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.