Покажем, как задачи с параметрами можно решать графически.
Найдём количество решений уравнения
в зависимости от $$ a$$.
Искомое количество решений совпадает с числом точек пересечения графиков функций
 |
График первой функции получается из графика функции, который был построен в предыдущем примере. Для этого нужно воспользоваться преобразованием вида ПР1 то есть график $$ y=_left(xright)$$ имеет такой вид, как показано на рис. 43 $$ fleft(0right)=sqrt$$.
Графиком функции $$ y=a$$ будет прямая, параллельная оси $$ Ox$$ (рис. 43). При этом она пересекает ось ординат в точке $$ (0,a)$$. Легко видеть, что при $$a 3$$ прямая $$ y=a$$ не имеет пересечений с графиком $$ y=_left(xright)$$, при $$ a=3$$ и $$ ain [0;sqrt)$$ есть две точки пересечения, а при $$ ain [sqrt;3)$$ – четыре общие точки и при $$ a=sqrt$$ – три общие точки. Остаётся лишь сформулировать ответ.
При $$ ain (-infty ;0)bigcup (3;+infty )$$ решений нет, при $$ ain [0;sqrt)bigcup left$$ – два решения, при $$ ain left<sqrtright>$$ – три решения, при $$ ain (sqrt;3)$$ – четыре решения.
Найдём количество решений уравнения в зависимости от $$ a$$:
 |
Методом интервалов нетрудно построить график функции
Количество решений уравнения совпадает с числом точек пересечения этого графика с прямой $$ fleft(xright)=a$$ (рис. 44).
Проанализировав график, несложно выписать ответ.
При $$ ain (8;+infty )$$ уравнение имеет 2 решения, при $$ a=8$$ уравнение имеет бесконечно много решений, при $$ ain (-infty ;8)$$ решений нет.
Рассмотрим ещё один пример задач с параметром, где используется построение множеств, задаваемых уравнениями с модулем. Напомним, что графиком уравнения называют линию на плоскости, на которой лежат те и только те точки, координаты которых удовлетворяют этому уравнению.
Найдём количество решений системы уравнений
в зависимости от $$ a$$.
Для решения необходимо построить график уравнения $$ left|xright|+left|yright|=4$$. Это можно сделать, последовательно выполнив построения таких графиков:
График второго уравнения – окружность с центром в точке $$ O(0;0)$$ и радиусом $$ left|aright|$$. Изобразим оба этих графика на координатной плоскости $$ xOy$$.
Как видим, при $$|a| 4$$ графики не пересекаются. При $$ left|aright|=2sqrt$$ или $$ left|aright|=4$$ есть 4 точки пересечения. При остальных $$ a$$ есть 8 точек пересечения. Таким образом, можно сформулировать ответ.
При $$ ain (-infty ;-4)cup (-2sqrt;2sqrt)cup (4;+infty )$$ система не имеет решений;
при $$ ain <-4;-2sqrt;2sqrt;4>$$ система имеет 4 решения;
при $$ ain (-4;-2sqrt)cup (2sqrt;4)$$ система имеет 8 решений.
В следующей задаче нам потребуется понятие локального экстремума функции. Говорят, что функция $$ y=fleft(xright)$$ имеет локальный максимум в точке $$ _$$, если для некоторого числа $$ε > 0$$ при $$|x − x_0| 0$$ при $$|x − x_0| 0$$ график $$ y=at-3$$ касается линии $$ y=sqrt$$ (cм. рис. 46). Уравнение $$ D=0$$ имеет единственный положительный корень `a=1/4`. Следовательно, `a_2=1/4`. Если $$dfrac3leq a 1/4` они не имеют общих точек.
Рассмотрим пример использования этого правила в задаче.
Найдём все значения параметра $$ a$$, при которых система
имеет хотя бы одно решение.
Неравенство системы после выделения полных квадратов можно записать в виде $$ ^-8left|xright|+16+^-8left|yright|+16le 1$$ или $$ left(right|x|-4^+(left|yright|-4^le 1$$. Множество $$ E$$ решений этого неравенства – объединение кругов $$ _$$, $$ _$$, $$ _$$, $$ _$$ (вместе с их границами) радиуса $$ 1$$ (см. рис. 47) с центрами $$ _(4;4)$$, $$ _(4;-4)$$, $$ _(-4;-4)$$, $$ _(-4;4)$$. Запишем уравнение системы в виде
 |
Это уравнение задаёт окружность $$ L$$ радиуса $$ left|aright|$$ с центром в точке $$ M(0;1)$$, или точку $$ (0;1)$$ при $$ a=0$$. Исходная система имеет хотя бы одно решение при тех значениях $$ a$$, при которых окружность $$ L$$ имеет общие точки с множеством $$ E$$. При этом ввиду симметричного расположения соответствующих пар кругов относительно оси ординат достаточно выяснить, при каких значениях $$ a$$ окружность $$ L$$ имеет общие точки с кругами, центрами которых являются точки $$ _$$ и $$ _$$. Проведём из точки $$ M$$ лучи $$ _$$ и $$ _$$ в направлении точек $$ _$$ и $$ _$$. Пусть $$ _$$ и $$ _$$ – точки пересечения $$ _$$ и окружности с центром $$ _$$, $$ _$$ и $$ _$$ – точки пересечения $$ _$$ и окружности с центром $$ _$$. Тогда из геометрических соображений имеем:
При $$ 4le left|aright|le 6$$ окружность с центром $$ M$$ имеет общие точки с кругом $$ _$$ , а при $$ sqrt-1le left|aright|le sqrt+1$$ – с кругом $$ _$$.
а) Если $$b 0$$. Эта система не имеет решений при $$ a=0$$ и поэтому $$b 0$$. Теперь мы прибегнем к графическому методу. Рассмотрим два случая: $$0 1$$. Если $$b > 1$$, то $$sqrt Эта система не имеет решений, так как прямая $$ y=x-b$$ не пересекает график функции $$ y=|^-b|$$ (см. рис. 48). Если $$0 0$$).
В завершении разберём несколько задач с параметрами, которые удобно решать методом областей на координатной плоскости.
Найдём все значения `a`, при каждом из которых уравнение
Рассмотрим функции `f(x)-a|x-3|` и `g(x)=5/(x+2)`.
Если построить график функции `f(x)` для разных `a` (рис. 50) и график функции `g(x)` (рис. 51), то можно без проблем исследовать на промежутке `[0;+oo)` уравнение `f(x)=g(x)`.
При `a При `a>0` функция `f(x)` возрастает на промежутке `(3;+oo)`. Функция `g(x)` убывает на этом промежутке, поэтому уравнение `f(x)=g(x)` всегда имеет ровно одно решение на промежутке `(3;+oo)`, поскольку `f(3) g(3+1/a)`. На промежутке `[0;3]` уравнение `f(x)=g(x)` принимает вид `3a-ax=5/(x+2)`. Это уравнение сводится к уравнению `ax^2-ax+(5-6a)=0`. Будем считать, что `a>0`, поскольку случай `a
Пусть уравнение имеет два корня, то есть `a>4/5`. Тогда оба корня меньше `3`, поскольку при `x>=3` значения функции `3a-ax` неположительны, а значения функции `5/(x+2)` положительны. По теореме Виета сумма корней равна `1`, а произведение равно `5/6-6`. Значит, больший корень всегда принадлежит промежутку `[0;3]`, а меньший принадлежит этому промежутку тогда и только тогда, когда `5/a-6>=0`, то есть `a 5/6`;
– три корня при `4/5
В завершении разберём несколько задач с параметрами, которые удобно решать методом областей на координатной плоскости. В следующем примере будем использовать известный подход к задачам, содержащим некоторые переменные в квадрате. Суть этого подхода — рассмотрение выражения как квадратичной функции относительно какой-нибудь переменной (остальные переменные при этом считаются параметрами) с последующим использованием известных свойств квадратичной функции.
Найдём все значения параметра $$ a$$, при каждом из которых система уравнений
имеет ровно три решения.
Первое уравнение данной системы равносильно совокупности двух уравнений $$ |y+9|+|x+2|=2$$ и $$ ^+^=3$$. Первое из них задаёт квадрат $$ G$$ с центром $$ (-2;-9)$$, диагонали которого равны $$ 4$$ и параллельны осям координат. Второе задаёт окружность $$ S$$ с центром $$ (0;0)$$ радиуса $$ sqrt$$ (см. рис. 52).
 |
Второе уравнение исходной системы при $$a > 0$$ задаёт окружность $$ Omega $$ с центром $$ (-2;-4)$$ радиуса $$ R=sqrt$$.
Отметим, что при $$a Рассмотрев случаи внешнего и внутреннего касания окружностей $$ Omega $$ и $$ S$$, можно заключить, что они имеют ровно `1` общую точку при $$ R=sqrtpm sqrt$$, ровно `2` общие точки при $$ Rin (sqrt-sqrt;sqrt+sqrt)$$ и ни одной общей точки при остальных $$ R$$. Поскольку центры окружности $$ Omega $$ и квадрата $$ G$$ лежат на прямой $$ x=-2$$, то $$ Omega $$ и $$ G$$ имеют ровно `1` общую точку при $$ R=3$$ или $$ R=7$$, ровно `2` общие точки при $$ Rin (3;7)$$ и ни одной общей точки при остальных значениях $$ R$$. Для того чтобы у системы было 3 решения, необходимо и достаточно, чтобы окружность $$ Omega $$ имела `2` общие точки с квадратом $$ G$$ и `1` общую точку с окружностью $$ S$$ или наоборот. Рассмотрим значения $$ R$$, при которых окружность $$ Omega $$ имеет с квадратом $$ G$$ или окружностью $$ S$$ ровно `1` общую точку.
1) $$ R=sqrt+sqrt$$. Тогда есть ровно `1` общая точка с окружностью $$ S$$, и ровно `2` общие точки с квадратом $$ G$$ (т. к. $$3 sqrt + sqrt$$), т. е. у системы 1 решение.
Итак, подходят $$ R=3$$ и $$ R=sqrt+sqrt$$. Тогда искомые значения параметра $$ a=^=9$$ и $$ a=(sqrt+sqrt^=23+4sqrt$$.
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать
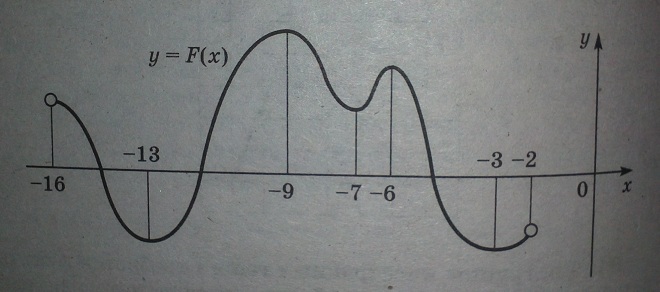
03. В9. На рисунке изображен график первообразной y=F(x) некоторой функции y=f(x), определенной на интервале (-16; -2).
Задача.
На рисунке изображен график первообразной y=F(x) некоторой функции y=f(x), определенной на интервале (-16; -2). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-14;-8].
Решение:
По определению первообразной имеем F′(x) = f(x).
Нас просят найти количество точек, в которых f(x) = 0, то есть F′(x) = 0.
На рисунке изображен график функции у = F(x). Производная этой функции F′(x) равна нулю в точках максимума и минимума.
На отрезке [-14; -8] таких точек всего две — это х1 = -13 — точка минимума и х2 = -9 — точка максимума.
Поэтому F′(x) равно нулю в этих точках на отрезке [-14; -8].
Значит, количество решений уравнения f(x) = 0 или что тоже самое F′(x) = 0 будет иметь 2 решения.
Видео:7 класс, 35 урок, Графическое решение уравненийСкачать
Метод подсчёта количества решений
Линейные алгебраические уравнения — одни из самых простых уравнений, которые мы можем решить. Если в уравнении только одна переменная, решение тривиально, в то время как для системы линейных уравнений существует множество способов найти уникальные решения.
В этой статье нас интересует частный случай линейного уравнения с несколькими переменными. Хорошо известно, что подобное уравнение имеет бесконечное число решений. Мы наложим определённые ограничения и в значительной степени сократим количество решений.
Общая форма интересующего нас уравнения:
где n и m — положительные целые числа.
Наша задача — найти число решений этого уравнения, предполагая, что xᵢ являются целыми числами. Это предположение значительно снижает число решений заданного уравнения.
Видео:На рисунке изображен график функции. Найдите количество решений уравнения производная=0Скачать
Нам нужен метод
Давайте начнём с частного случая общего уравнения:
Нетрудно найти все решения этого уравнения методом простого счёта. Решения заданы парами (x₁, x₂):
Мы видим, что уравнение имеет шесть решений. Также нетрудно предположить, что, если мы заменим правую часть определённым положительным целым числом m, решения будут выглядеть так:
и мы сможем подсчитать число решений — m+1.
Это было просто, верно?
Теперь возьмём немного более сложный вариант с тремя переменными, скажем:
С несколько большими усилиями, чем в предыдущем примере, находим решения в виде наборов из трёх чисел (x₁, x₂, x₃):
Число решений в этом случае равно 10.
Легко представить, что метод прямого счёта может стать очень утомительным для уравнения с большим количеством переменных. Он также становится утомительным, если целое число в правой части уравнения становится больше — например, если в правой части у нас будет 8, а не 3, решений будет уже 45. Разумеется, не хотелось бы искать все эти решения методом прямого счёта.
Значит, нужен эффективный метод.
Видео:Алгебраическое определение количества решений системы линейных уравнений | Алгебра IСкачать
Разрабатываем метод
Существует ещё один способ, которым можно решить предыдущие два уравнения. Давайте снова начнём с этого уравнения:
Одним из решений было (5, 0). Давайте преобразуем его в:
Мы разложили решение на нули и единицы, соответствующие каждому числу. Ненулевую часть (в данном случае 5) мы разложили на соответствующее число единиц, а ноль преобразовали в ноль. Таким же образом мы можем разложить и другое решение:
Мы поменяли прежнее расположение нуля, чтобы получить новое решение. Итак, два числа в парах (обозначенные красным и голубым) разделены нулём (чёрный) в разложенном виде. Таким же образом запишем оставшиеся решения:
Записав решения таким образом, видим закономерность. Кажется, все решения — это просто перестановки нулей и единиц. Вопрос о том, сколько существует решений, становится эквивалентным вопросу как много таких перестановок нулей и единиц может быть сделано, начиная с любой из конфигураций.
В данном случае у нас есть 6 местоположений в разложенной конфигурации для размещения нулей и единиц. Мы можем выбрать простейшее решение в качестве начальной конфигурации:
Теперь всё, что нам нужно найти, это общее число способов, которыми можно заполнить шесть местоположений пятью единицами и одним нулём.
Подобные задачи подсчёта мы можем решить различными способами, но наиболее эффективным будет способ, разработанный в такой области математики как комбинаторика, которая даёт нам формулу для числа способов перестановки r объектов в n местоположений:
где n! (читается как “n факториал”) определяется как произведение всех целых чисел от 1 до n, т.е. n! = 1 × 2 × 3 × ⋅ ⋅ ⋅ × n. Мы также определяем 0! = 1.
Эта формула обычно записывается в компактной форме как:
Теперь, возвращаясь к задаче, мы можем использовать эту формулу для нахождения числа способов перестановки пяти единиц в шести местоположениях:
Это то же самое число, что мы получили методом прямого счёта!
Выглядит многообещающе, поэтому давайте проверим, сможем ли мы найти таким способом число решений второго линейного уравнения:
Некоторые решения можно записать в разложенном виде:
В этот раз нам нужно заполнить тремя единицами и двумя нулями пять местоположений. Используя формулу мы можем найти число способов расположения чисел:
И опять то же число, что мы получили методом прямого счёта. Мы можем также найти число решений для нерешённого случая, где в правой части уравнения 8 вместо 3. Одним из решений будет:
а нам нужно найти число способов разместить 8 единиц в 10 местоположениях, и это будет:
как и утверждалось выше.
Если мы уверены в том, что этот метод работает для всех случаев, нам нужна общая формула. Напомним, что общее уравнение имеет вид:
Простейшее решение этого уравнения:
Поскольку существует n переменных, количество нулей в этом решении равно n-1. Таким образом, разложение выглядит так:
В разложенной конфигурации видим m и n-1 нулей (как утверждалось выше).
Следовательно, общее число местоположений, которые нужно заполнить, равно (m+n-1). Единственное, что остаётся — найти число способов, которыми можно заполнить m+n-1 местоположений m единиц, что определяется по формуле:
📹 Видео
Графический способ решения систем уравнений. Алгебра, 9 классСкачать
Исследование возможного количества решений уравнения с параметром при помощи графикаСкачать
ЕГЭ 2017 Профильный №7 найдите по графику функции - где производная равна нулю #7Скачать
Сколько решений имеет лог. уравнение (!(A *B) + C) IMP (!A * !B + D) = 1. Информатика, ЕГЭ, логикаСкачать
Алгебра 9 класс. Графическое решение систем уравненийСкачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Решение системы неравенств с двумя переменными. 9 класс.Скачать
Задача 7 ЕГЭ на производную и первообразную #29Скачать
Система уравнений не имеет решений или имеет бесчисленное множество решенийСкачать
Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать
Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать
Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать
#75 Урок 36. Определение количества решений системы уравнений. Алгебра 7 класс.Скачать
Задание 8 ЕГЭ профиль Найдите количество решений уравнения производная равна нулю 2.Скачать
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать
10 класс, 43 урок, Уравнение касательной к графику функцииСкачать
