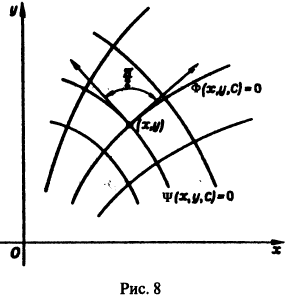
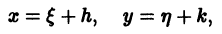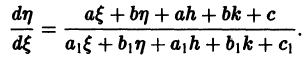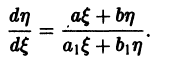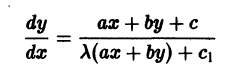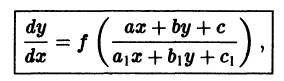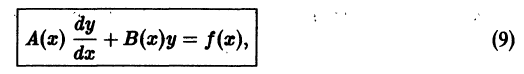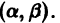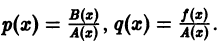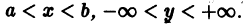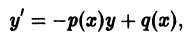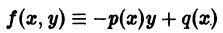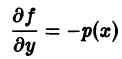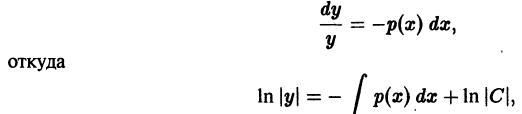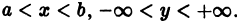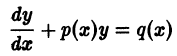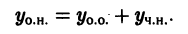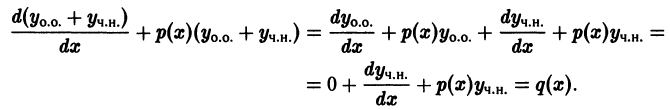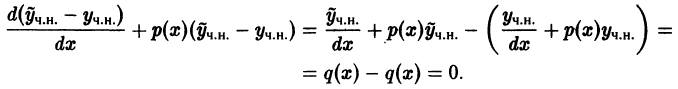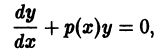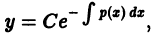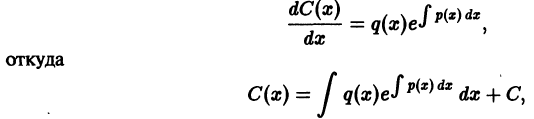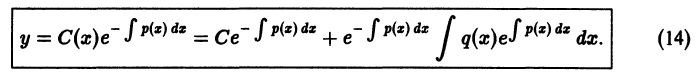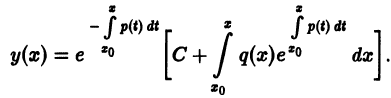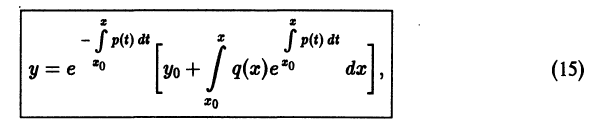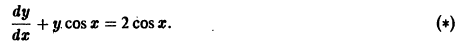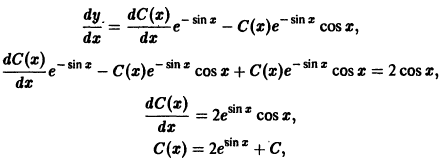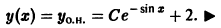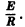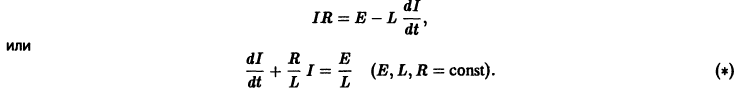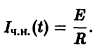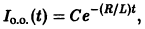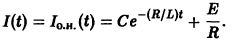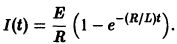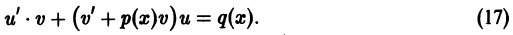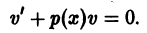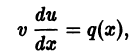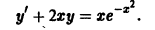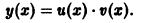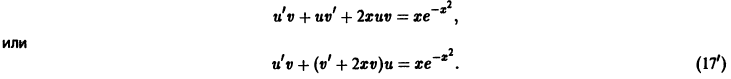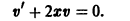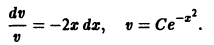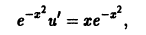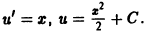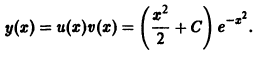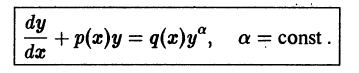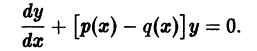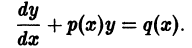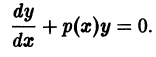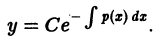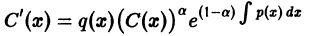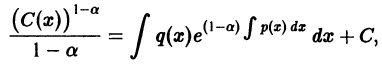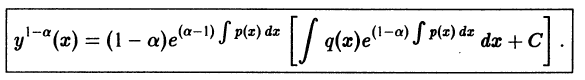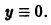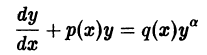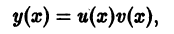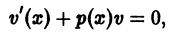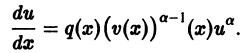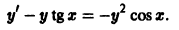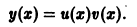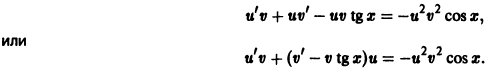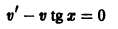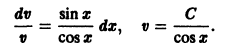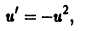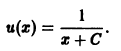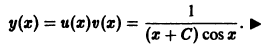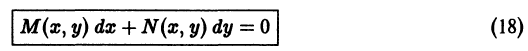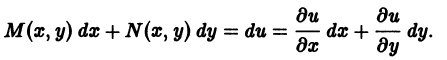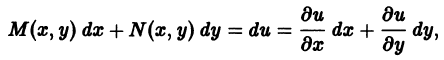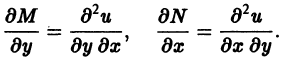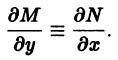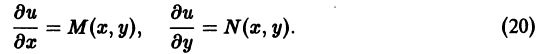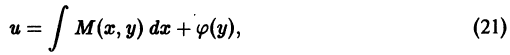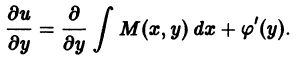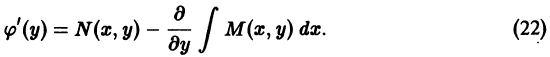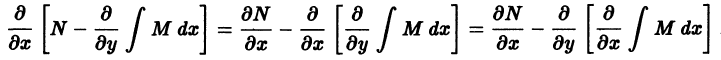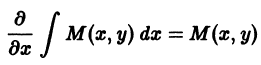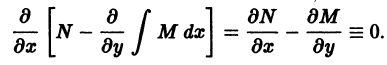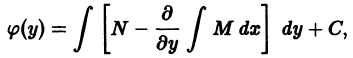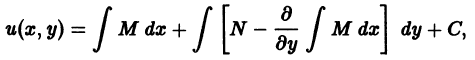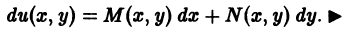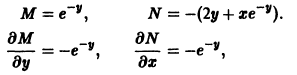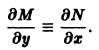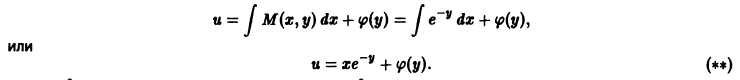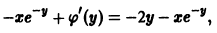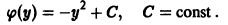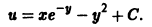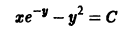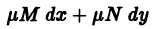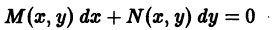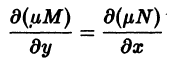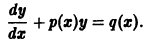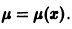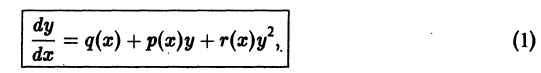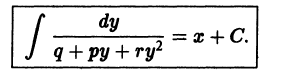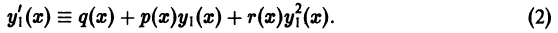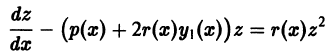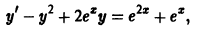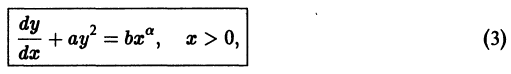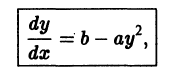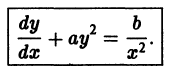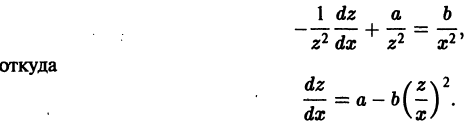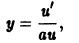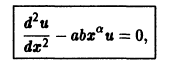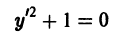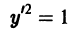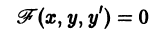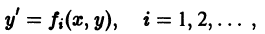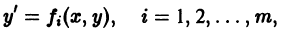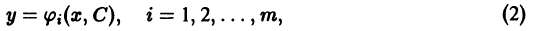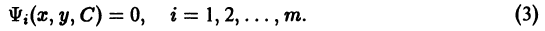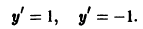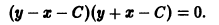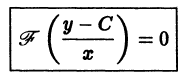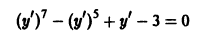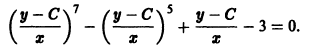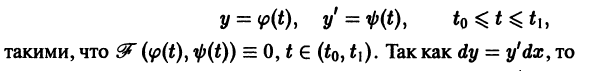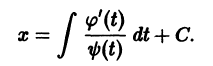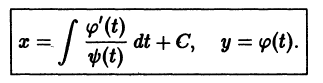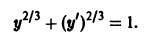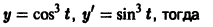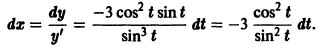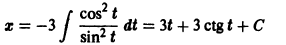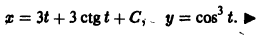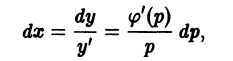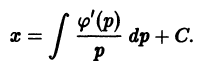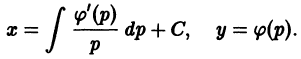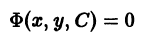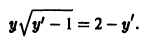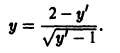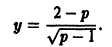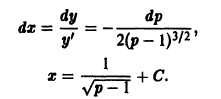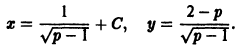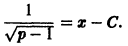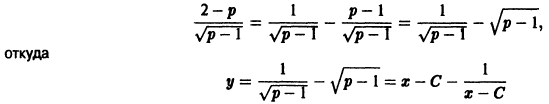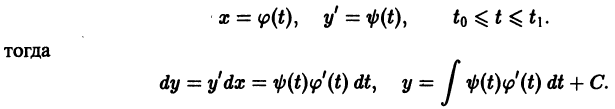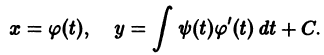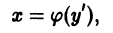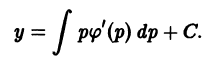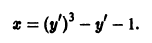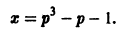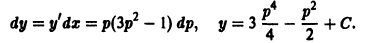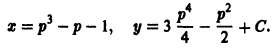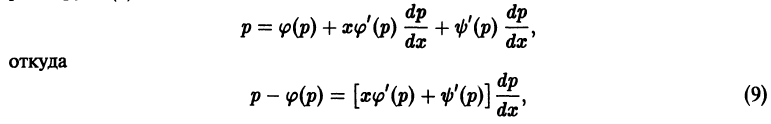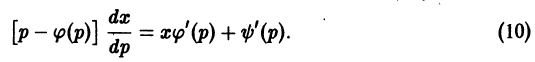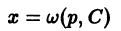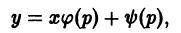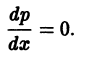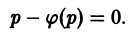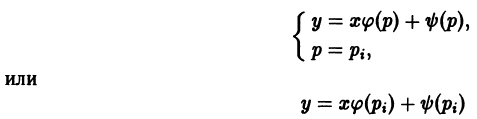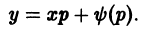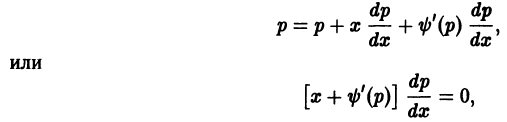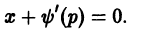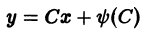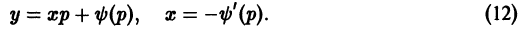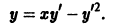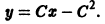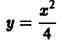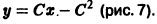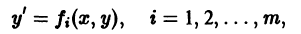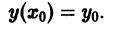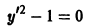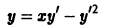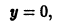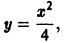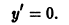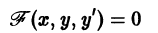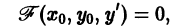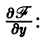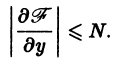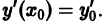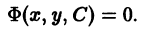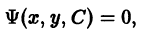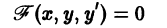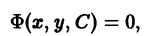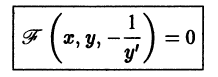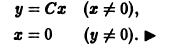Решение дифференциального уравнения
называется особым , если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку кроме этого решения проходит и другое решение, имеющее в точке ту же касательную, что и решение , но не совпадающее с ним в сколь угодно малой окрестности . График особого решения будем называть особой интегральной кривой уравнения (1). Если функция и ее частные производные и непрерывны по всем аргументам , то любое особое решение уравнения (1) удовлетворяет также уравнению
Значит, чтобы отыскать особые решения (1), надо исключить из уравнений (1) и (2).
Полученное после исключения из (1) и (2) уравнение
Часто бывает так, что распадается на несколько ветвей . Тогда нужно установить, является ли каждая в отдельности ветвь решением уравнения (1), и если является, то будет ли оно особым решением, т.е. нарушается ли единственность в каждой его точке.
Пример 1. Найти особые решения дифференциального уравнения
а) Находим p-дискриминантную кривую. В данном случае и условие (2) принимает вид , отсюда . Подставляя это выражение для в уравнение (4), получаем
Кривая (5) есть p-дискриминантная кривая уравнения (4): она состоит из одной ветви — параболы.
б) Проверяем, является ли p-дискриминантная кривая решением заданного уравнения. Подставляя (5) и ее производную в (4), убеждаемся, что есть решение уравнения (4).
в) Проверяем, является ли решение (S) особым решением уравнения (4). Для этого найдем общее решение уравнения (4). Перепишем (4) в виде . Это уравнение Клеро. Его общее решение
Выпишем условие касания двух кривых и в точке с абсциссой :
Первое равенство выражает совпадение ординат кривых, а второе выражает совпадение угловых коэффициентов касательных к этим кривым в точке с абсциссой .
Полагая , находим, что условия (7) принимают вид
Подставляя в первое из равенств (8), получаем или т.е. при первое равенство выполняется тождественно, так как есть абсцисса произвольной точки.
Итак, в каждой точке кривой (5) ее касается некоторая другая кривая семейства (6), а именно та, для которой . Значит, есть особое решение уравнения (4).
г) Геометрическое истолкование.
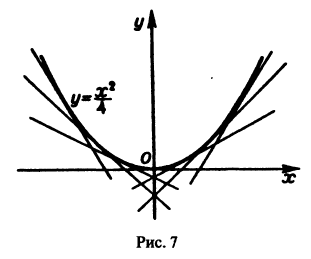
Общее решение уравнения (4) есть семейство прямых (6), а особое решение (5) является огибающей этого семейства прямых (рис. 19).
Огибающей семейства кривых
называется такая кривая, которая в каждой своей точке касается некоторой кривой семейства (9) и каждого отрезка которой касается бесконечное множество кривых из (9). Будем говорить, что кривые и касаются в точке , если они имеют в этой точке общую касательную.
Если (9) есть общий интеграл уравнения (1), то огибающая семейства кривых (9), если она существует, будет особой интегральной кривой этого уравнения. В самом деле, в точках огибающей значения совпадают со значениями для интегральной кривой, касающейся огибающей в точке , и, следовательно, в каждой точке огибающей значения удовлетворяют уравнению , т.е. огибающая является интегральной кривой.
Далее, в каждой точке огибающей нарушена единственность, так как через точки огибающей по одному направлению проходит, по крайней мере, две интегральные кривые: сама огибающая и касающаяся ее в рассматриваемой точке интегральная кривая семейства (9). Следовательно, огибающая является особой интегральной кривой.
Из курса математического анализа известно, что огибающая входит в состав C-дискриминантной кривой (коротко СДК), определяемой системой уравнений
Некоторая ветвь СДК заведомо будет огибающей, если на ней:
1) существуют ограниченные по модулю частные производные
где и — постоянные;
Замечание. Условия 1) и 2) лишь достаточны, а потому ветви СДК, на которых нарушено одно из этих условий, тоже могут быть огибающими.
Пример 2. Найти особые решения дифференциального уравнения
а) Находим C-дискриминантную кривую. Имеем , так что отсюда . Подставляя это значение в (14), получаем откуда
Это и есть C-дискриминантная кривая: она состоит из двух прямых и .
б) Непосредственной подстановкой убеждаемся, что каждая из ветвей СДК является решением уравнения (13).
в) Докажем, что каждое из решений (15) является особым решением уравнения (13). В самом деле, так как и , то на каждой ветви СДК имеем (предполагаем, что решение уравнения (13) рассматривается на отрезке
где — область допустимых значений .
Заметим, что на любой из ветвей СДК в области 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQCAMAAABncAyDAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAMRDQiiHowAFBoWFRoLFx3eb7ogAAAMZJREFUKM+1UksSwyAIVUHAX+T+p602mTYkdqZd1AUL5fk+4NzfjiQvv/QXwkz++/6kyblOYfXmMd4vNxglaF//xu0KEeJZdVYXkDFUbhaSDCDqDtDhO3ASgOypGJbMyVh4A3A8bBpQq1URM1exAEcTUHaF4R5ZzFQXDE+FuDIfET4AiqZFe+PykiQHYIbb8rAgTsAM3lvTjvc5DCVeORANFjSxbhfOqn6ux5wPICRojOf2fJ81Uscj+bmEUc5q4jKCXucmPQAaYQaRCPmIUQAAAABJRU5ErkJggg==» />, так дх что выполняется одно из условий (12). Значит, условия (11) и (12) выполняются, а, следовательно, прямые (15) являются огибающими парабол (14).
Итак, установлено, что каждое из решений (15) есть особое решение.
В вопросах отыскания особых решений оказываются полезными следующие символические схемы:
Схема (16) означает, что уравнение p-дискриминантной кривой может распадаться на три уравнения:
1) — уравнение огибающей;
2) — уравнение геометрического места точек заострения (возврата);
3) — уравнение геометрического места точек прикосновения интегральных линий, причем множитель входит в в квадрате.
Схема (17) означает, что уравнение C-дискриминантной кривой может распадаться на три уравнения:
1) — уравнение огибающей;
2) — уравнение геометрического места узловых точек, причем множитель входит в в квадрате;
3) — уравнение геометрического места точек заострения, причем множитель входит в в кубе.
Не обязательно, чтобы для каждой задачи все составные части и фигурировали в соотношениях (16) и (17).
Из всех геометрических мест только огибающая есть особое решение дифференциального уравнения. Отыскание огибающей упрощается тем, что в схемы (16) и (17) она входит в первой степени.
В отношении других геометрических мест (точек заострения, узловых точек и точек прикосновения) требуется дополнительный анализ в каждом конкретном случае. То обстоятельство, что некоторый множитель входит в в квадрате (и совсем не входит в ) указывает на то, что здесь может быть геометрическое место точек прикосновения интегральных линий. Аналогично, если некоторый множитель входит в в квадрате (и совсем не входит в ), то здесь может быть геометрическое место узловых точек. Наконец, если множитель входит в в первой степени, а в — в третьей, то возможно наличие геометрического места точек заострения.
Пример 3. Найти особое решение дифференциального уравнения
Решение. Особое решение, если оно существует, определяется системой
где второе уравнение (19) получено из (18) дифференцированием его по . Исключив , получим p-дискриминантную кривую , которая распадается на две ветви
Подстановкой убеждаемся, что обе функции являются решениями уравнения (18).
Чтобы установить, являются ли решения (20) и (21) особыми или нет, найдем огибающую семейства
являющегося общим интегралом для (18).
Выпишем систему для определения C-дискриминантной кривой откуда, исключая , получаем , или и , что совпадает с (20) и (21). В силу того, что на линиях (20) и (21) условия (11) и (12) выполняются, заключаем, что линии и являются огибающими, а значит (20) и (21) есть особые решения заданного уравнения.
Интегральные кривые (22) суть параболы , а линии — огибающие этого семейства парабол (рис. 20).
Пример 4. Найти особые решения дифференциального уравнения
Решение. Дифференцируем (23) по
Исключая из (23) и (24), получим . Дискриминантная кривая есть ось ординат. Она не является интегральной кривой уравнения (23), но согласно схеме (16) может быть геометрическим местом точек прикосновения интегральных кривых.
Решениями уравнения (23) являются параболы и те гладкие кривые, которые можно составить из их частей (рис. 21).
Из чертежа видно, что прямая действительно есть геометрическое место точек прикосновения интегральных кривых уравнения (23).
Пример 5. Найти особые решения дифференциального уравнения
Решение. Найдем . Исключая из системы уравнений получаем
Преобразовав уравнение (25) к виду , находим его общий интеграл .
Найдем . Исключая из системы уравнений будем иметь
Итак, из (26) и (27) имеем
Множитель входит в p-дискриминант и в C-дискриминант в первой степени и дает огибающую, т. е. функция есть особое решение дифференциального уравнения (25). Непосредственной подстановкой убеждаемся, что действительно удовлетворяет уравнению.
Уравнение , входящее во второй степени в p-дискриминант и совсем не входящее в C-дискриминант, дает место точек прикосновения .
Наконец, уравнение , входящее в C-дискриминант во второй степени и совсем не входящее в p-дискриминант, дает место узловых точек (рис.22).
Пример 6. Найти особые решения дифференциального уравнения
а) Ищем p-дискриминантную кривую. Дифференцируя (28) по , получаем , откуда
Подставляя (29) в (28), найдем уравнение :
б) Ищем общий интеграл уравнения (28). Обозначив у’ через р, перепишем (28) в виде
Дифференцируя обе части (28) по и учитывая, что , будем иметь
Приравнивая нулю первый множитель , получаем (29), а соотношение дает
Исключая параметр из уравнений (31) и (32), найдем общее решение уравнения (28):
в) Находим C-дискриминантную кривую. Дифференцируя (33) по C, будем иметь
Подставляя (34) в (33), получаем уравнение .
Согласно символическим схемам (16) и (17) заключаем, что есть огибающая семейства полукубических парабол (33), а есть геометрическое место точек заострения (множитель входит в уравнение в кубе) (рис. 23). Подстановкой в уравнение (28) убеждаемся, что есть решение, а решением не является (при уравнение (28) не имеет смысла). Таким образом, решение есть особое (огибающая семейства интегральных линий).
- Как найти интегральную кривую уравнения
- 3.2. Определение дифференциального уравнения и связанных с ним общих понятий.
- 3.3. Дифференциальные уравнения первого порядка как поле направлений.
- 3.4. Задача Коши.
- 3.5. Основные методы интегрирования дифференциальных уравнений первого порядка.
- Дифференциальные уравнения первого порядка
- I. Уравнения с разделяющимися переменными
- II. Уравнения, однородные относительно переменных
- III. Уравнения в полных дифференциалах
- IV. Линейные дифференциальные уравнения
- 3.6. Особое решение дифференциального уравнения. Уравнение Клеро.
- 3.7. Уравнение Бернулли.
- 3.9. Дифференциальные уравнения, допускающие понижение порядка.
- 3.10. Линейные дифференциальные уравнения n-го порядка. Общая теория.
- 3.12. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
- 3.13. Неоднородное линейное дифференциальное уравнение, структура общего решения. Принцип наложения.
- 3.14. Подбор частных решений линейного неоднородного дифференциального уравнения с постоянными коэффициентами и со специальной правой частью.
- 3.15. Метод вариации произвольных постоянных.
- Дифференциальные уравнения первого порядка с примерами решения и образцами выполнения
- Эквивалентные дифференциальные уравнения. Задача Коши
- Теорема существования и единственности решения задачи Коши для уравнения у’ = f(x, у)
- Приближенные методы интегрирования уравнения у’ = f(x, у)
- Метод изоклин
- Метод последовательных приближений
- Численные методы решения задачи Коши Метод Эйлера
- Понятие о методе Рунге—Кутта
- Некоторые виды уравнений, интегрируемых в квадратурах
- Уравнения с разделяющимися переменными
- Уравнения, однородные относительно x и у
- Линейные дифференциальные уравнения
- Уравнение Бернулли
- Уравнения в полных дифференциалах
- Уравнение Риккати
- Дифференциальные уравнения, не разрешенные относительно производной
- Уравнение Лагранжа
- Уравнение Клеро
- Геометрические вопросы, связанные с дифференциальными уравнениями 1-го порядка. Ортогональные траектории
- Ортогональные траектории
- Дополнение к дифференциальным уравнениям первого порядка
- 📺 Видео
Видео:Найти все интегральные кривые уравненияСкачать

Как найти интегральную кривую уравнения
Многие процессы в природе можно описать с помощью функции. Дифференциальное исчисление позволяет по данной функции исследовать ее свойства. Не менее важна и обратная задача: по данным свойствам функции найти эту функцию. Иными словами, исследуя процесс, найти функцию, которая его описывает.
В алгебре для нахождения неизвестных величин пользуются уравнениями: по условию задачи составляют соотношение, связывающее неизвестную величину с данными и, решая его, находят неизвестную. Аналогично в анализе для нахождения неизвестной функции по данным ее свойствам составляют уравнение, связывающее неизвестную величину с величинами, задающими ее свойство. Поскольку свойства выражаются через производные или дифференциалы того или иного порядка, приходят к соотношению, связывающему функцию, ее производные или дифференциалы. Это соотношение называется дифференциальным уравнением, решая его, находят искомую функцию.
Рассмотрим задачи, приводящие к понятию дифференциального уравнения.
Задача 1. На плоскости XOY найти кривую, которая в каждой своей точке имеет касательную, образующую с положительным направлением оси Ox угол, тангенс которого равен удвоенной абсциссе точки касания.
Решение. Пусть уравнение искомой кривой y = f (x).
Обозначим через α угол, образованный касательной МТ с положительным направлением оси Ох. Как известно, угловой коэффициент касательной МТ есть tg α, и он равен производной от y по x, так что
С другой стороны, по условию задачи имеем
Приравнивая значения tg α, определяемые формулами (1.1) tg α = y ‘ и (1.2) tg α = 2x получим
Решением дифференциального уравнения (1.3) y ‘ = 2x является любая первообразная для функции 2x. Например, решением будет
Как известно из интегрального исчисления, все первообразные для функции 2x и, следовательно, все решения дифференциального уравнения (1.3) y ‘ = 2x даются формулой
где С — произвольная постоянная.
Дифференциальное уравнение имеет бесчисленное множество решений, т.е. условию задачи удовлетворяет не одна кривая, а целое семейство кривых — парабол. Но если в условие задачи добавить точку M0 (x0, y0), через которую проходит искомая кривая, то получим единственную кривую. Для этого достаточно заменить в уравнении (1.5) y = x 2 + С координаты x и y координатами точки M0
и, найдя из полученного уравнения значение произвольной постоянной С, подставить его в уравнение (1.5) y = x 2 + С . Выполняя указанные выкладки, имеем:
С = y0 – 

Таким образом, искомой кривой будет парабола
y = x 2 – 
Задача 2. Предположим, что материальная точка P движется по прямой, которую принимаем за ось Ox. Пусть известна скорость движения как функция от времени t; обозначим ее через f (t) и будем предполагать, что она непрерывна при всех рассматриваемых значениях времени t. Требуется найти закон движения точки, т. е. зависимость x от t, х = x(t), если известно, что в некоторый момент времени t0 точка занимает положение x0, так что x(t0) = x0. 
Решение. Известно, что скорость движения рассматриваемой точки в момент времени t равна производной от x по t. С другой стороны, эта скорость равна f (t). Поэтому

Равенство (1.7) 

Интегрирование уравнения (1.7) 
x = 
Выделим решение (движение), в котором
Для этого положим в формуле (1.8) x = 
x0 = 
откуда C = x0; следовательно, искомым решением (движением) будет
x = 
Формула (1.10) x = 

Условие (1.9) x = x0 при t = t0 называется начальным условием, а числа t0 и x0 — начальными данными решения (движения).
3.2. Определение дифференциального уравнения и связанных с ним общих понятий.
x 

то оно называется уравнением с частными производными.
В дальнейшем будем рассматривать только обыкновенные дифференциальные уравнения.
Не всегда удается получать решения в явном виде, например
Аналогично определяются общий интеграл и частный интеграл дифференциального уравнения.
Например, все решения уравнения
y’ =
y = 
3.3. Дифференциальные уравнения первого порядка как поле направлений.
Если его возможно разрешить относительно производной y ‘, то оно приводится к виду y ‘ = f (x, y). (3.1)
Такая форма дифференциального уравнения первого порядка называется нормальной, а уравнение является разрешимым относительно производной от искомой функции.
Выясним геометрический смысл дифференциального уравнения первого порядка вида (3.1) y ‘ = f (x, y) .
Общее решение геометрически задает однопараметрическое семейство интегральных кривых.
Решение y = y (x) уравнения (3.1) y ‘ = f (x, y) представляет собой на плоскости XOY кривую, а y ‘ — угловой коэффициент касательной к этой кривой в точке M (x, y). Уравнение (3.1) y ‘ = f (x, y) дает, таким образом, соотношение между координатами точки и угловым коэффициентом касательной к интегральной кривой в этой точке.
Задание уравнения (3.1) y ‘ = f (x, y) означает, что в каждой точке M (x, y) области, где определена функция f (x, y), задано направление касательной к интегральной кривой в точке M (x, y). Значит, имея уравнение (3.1) y ‘ = f (x, y) мы получаем поле направлений. Это поле графически можно изобразить, поместив в каждой точке M (x, y) черточку, наклоненную к оси Ox под углом, тангенс которого равен f (x, y).
Задача интегрирования уравнения (3.1) y ‘ = f (x, y) заключается в том, чтобы найти семейство кривых, у которых касательная к каждой точке совпадает с направлением поля в этих точках. Такое истолкование уравнения (3.1) y ‘ = f (x, y) дает графический способ построения его решения.
y ‘ = 
Это значит, что интегральные кривые пересекают эту линию под одним и тем же углом

т.е. все черточки параллельны для всех точек изоклины.
Давая p различные значения, получим ряд изоклин или линий постоянного наклона касательных. Чтобы получить, приближенный график решения, проходящий через данную точку M0 (x0, y0), проводим кривую так, чтобы она пересекала изоклину под углами, указанными черточками и проходила через точку M0 (x0, y0).
Установим связь между уравнением (3.2) y ‘ = 

есть интегральная кривая этого уравнения, проходящая через точку M (x, y). Проведем касательную к интегральной кривой (3.3) y = y (x) в точке M и обозначим через α угол, образованный касательной MT с положительным направлением оси x.
Таким образом, если через точку M(x, y) проходит интегральная кривая (3.3) y = y (x) , то наклон касательной к ней в этой точке определяется формулой
так что наклон касательной к интегральной кривой определен заранее самим дифференциальным уравнением.
Наклоны касательных можно указать, не находя интегральных кривых. Для этого построим в каждой точке M области G отрезок (для определенности — единичной длины) с центром в точке M, составляющий с положительным направлением оси Ox угол α, тангенс которого определяется формулой (3.4) tg α = f (x, y) . Получим так называемое поле направлений, определяемое уравнением (3.2) y ‘ = 

Чтобы ответить на вопрос, под каким углом интегральные кривые могут пересекать ось x, достаточно подставить в правую часть уравнения (3.2) y ‘ = 
Например, интегральные кривые уравнения

пересекают ось x под углом α, тангенс которого равен x 2 . Аналогично интегральные кривые уравнения (3.2) y ‘ = 
Вообще, если надо узнать, какой угол с осью x образуют интегральные кривые уравнения (3.2) y ‘ = 

Например, для интегральных кривых уравнения

в точках их пересечения с прямой y = y имеем tg α = 0, так что касательные к этим интегральным кривым параллельны оси x.
Кривая ω (x, y) = 0, в каждой точке которой направление поля, определяемое дифференциальным уравнением (3.2) y ‘ = 
Уравнения изоклин дифференциального уравнения (3.2) y ‘ = 
где k = tg α = const. Например, для уравнения (3.5) 
вырождающиеся в точку (0,0) при k = 0. При k = 1 получаем изоклину
Интегральные кривые в каждой точке этой окружности наклонены к оси x под углом α. С увеличением k наклон интегральных кривых возрастает, и интегральные кривые имеют вид, указанный схематически на рисунке. Построив достаточно «густое» семейство изоклин (в нашем случае — окружностей); можно получить методом изоклин сколь угодно точное представление об интегральных кривых.
Если в точке M(x, y) правая часть уравнения (3.2) y ‘ = 


Таким образом, во всякой точке M(x, y), в которой правая часть уравнения (3.2) y ‘ = 




3.4. Задача Коши.
Дифференциальное уравнение обычно имеет бесчисленное множество решений. Для того, чтобы из всех решений выделить одно, надо задать какое-либо конкретное значение функции при некотором значении независимого переменного. Задать значение y0 искомой функции при некотором значении x0 независимого переменного — это значит задать начальное условие

С геометрической точки зрения задача отыскания решения дифференциального уравнения с заданным начальным условием равносильна тому, чтобы найти ту интегральную кривую, которая проходит через точку M0 (x0, y0) на плоскости XOY.
Естественно возникает вопрос: всегда ли существует решение дифференциального уравнения, удовлетворяющее данному начальному условию, и, если существует, то будет ли оно единственным?
Ответ на поставленные вопросы дает теорема существования и единственности решения дифференциального уравнения первого порядка.
Пусть дано уравнение y’ = f (x, y) с начальным условием 
- В прямоугольнике R, определенном неравенствами
функция f (x, y) непрерывна. Из этого условия вытекает, что в замкнутой области R функция f (x, y) ограничена, т.е. существует действительное число M > 0 такое, что для любой точки (x, y) ∈ R | f (x, y)| ≤ M.
Обозначим через h меньшее из двух чисел a, 
При данных условиях существует единственное решение y = y(x), где x0 – h ≤ x ≤ x0 + h, удовлетворяющее начальному условию 
3.5. Основные методы интегрирования дифференциальных уравнений первого порядка.
Дифференциальные уравнения первого порядка
где
- y’ =
.
- Разделить переменные.
- Проинтегрировать.
- Замена
= u, где u = u(x).
- После подстановки получим уравнение с разделяющимися переменными.
- Решив его, заменим u =
.
- Проверяем
.
Решением дифференциального уравнения является u(x, y), где= M(x, y),
= N(x, y).
- y’ + P(x) y = 0 — линейное однородное дифференциальное уравнение с разделяющимися переменными.
- y’ + P(x) y = Q(x)
- метод вариации произвольной постоянной;
- метод Бернулли:
y = u(x) · v(x).
I. Уравнения с разделяющимися переменными
Дифференциальное уравнение вида y’ = f (x) g ( y) или M(x) N( y) dx + P(x) Q ( y) dy = 0 называется уравнением с разделяющимися переменными.
Можно сделать преобразование так, чтобы в одной части была одна переменная, в другой — другая.


где 

Общий интеграл, выраженный в квадратурах:




Частный интеграл, удовлетворяющий условию 




Если работать с уравнением y’ = f (x) g ( y), то 
Замечание. Необходимо учесть, что при делении на P(x) и N(y), мы могли потерять решение уравнения, поэтому нужно проверить, не являются ли решениями данного уравнения, не вошедшие в общее решение, решения уравнений P(x) = 0 и N(y) = 0.
Действительно, всякое решение, например y = y0, уравнения N(y) = 0 является решением уравнения
Значит решения y = y0, x = x0 являются интегралами уравнения (5.1) M(x) N( y) dx + P(x) Q ( y) dy , даже если они не содержатся в общем решении.
II. Уравнения, однородные относительно переменных
Пусть имеем дифференциальное уравнение y’ = f (x, y), однородное относительно переменных x и y. Положив t = 



Обозначив f 





Как интегрируется уравнение y’ = φ
Оно сводится к уравнению с разделяющимися переменными. Для этого делают замену

где u — новая искомая функция от независимой переменной x, т.е. u = u(x).
Дифференцируя по x, имеем:
тогда данное уравнение примет вид:

Это есть дифференциальное уравнение с разделяющимися переменными, преобразовав которое, получим:










причем |x| не пишем, т.к. –1 войдет в постоянную C.
После взятия квадратуры, подставляем u = 
Замечание. Мы делили на φ(u) – u, предполагая, что оно отлично от нуля.
- Если φ(u) ≡ u, то уравнение y’ = φ(u) примет вид: y’ =
— уравнение с разделяющимися переменными.
- Если φ(u) = u при некоторых значениях u = u0, то функция y = u0x — решение уравнения y’ = φ(u), которое может и не вытекать из общего.
y’ = u0 и φ

III. Уравнения в полных дифференциалах
Если существует функция u(x, y) такая, что
M(x, y) = 

то дифференциальное уравнение
можно переписать в форме


В этом случае, данное уравнение имеет решение
Другой вопрос, как найти эту функцию u(x, y)?
Это можно сделать с помощью криволинейного интеграла, но на практике поступают следующим образом.
Т.к. 
u(x, y) = 
где C(y) — функция, зависящая только от y и пока нам неизвестная. Будем ее искать из условия, что 





Отсюда находим C’(y), а интегрированием найдем C(y), которое затем подставляем в (5.3) и получаем u(x, y). Тогда общий интеграл уравнения (5.2) M(x, y) dx + N(x, y) dy = 0 имеет вид
IV. Линейные дифференциальные уравнения
Рассмотрим линейное однородное дифференциальное уравнение y’ + P(x) y = 0. Это и уравнение с разделяющимися переменными, значит,


Проинтегрируем последнее уравнение:



ln y = ln C – 
Общее решение линейного однородного дифференциального уравнения имеет вид
y = C
Общее решение линейного неоднородного уравнения можно найти:
его общее решение y = C
Ищем решение данного линейного неоднородного дифференциального уравнения в виде
y = C(x)
где C(x) — искомая функция от x.
Так как это решение дифференциального уравнения, то найдем y’:
y’ = C’(x) 

и, подставив в данное уравнение, получим
C’(x) = Q(x)
Интегрированием находим C(x):
C(x) = 

Найденную функцию C(x) подставляем в (5.4) y = C(x) 
2. Методом Бернулли.
На примере решения уравнения y’ – 
Пусть решение имеет вид:
u’v + v’u – 
u’v + u

Пусть v’ – 




v = x 3 , подставим в уравнение ( ∗ ),
u’ = 
Интегрированием находим u:
u = 


y = 


3.6. Особое решение дифференциального уравнения. Уравнение Клеро.
Решение y = y(x), в каждой точке которого нарушается единственность решения задачи Коши, называется особым решением. Особое решение не может быть получено из формулы общего решения y = φ(x, C) (6.1) при конкретном числовом значении произвольной постоянной C (но может быть получено при C = C(x)).
Если правая часть уравнения 



Кривые, подозрительные на особые решения, могут быть иногда найдены по уравнению семейства интегральных кривых.
Огибающая семейства интегральных кривых уравнения (6.2) 


Отметим, наконец, что особые решения всегда можно обнаружить в процессе нахождения общего решения (общего интеграла) дифференциального уравнения. Дело в том, что когда делим обе части данного дифференциального уравнения на некоторую функцию ω(x, y), то получаем уравнение, вообще говоря, не равносильное данному, ибо можем при этом потерять решения вида y = φ(x) при x = ψ(y), при которых делитель ω(x, y) обращается в нуль, если эти решения не содержатся в общем решении, т. е. не получаются из него ни при каких числовых значениях произвольной постоянной (включая ± ∞). Решения, о которых идет речь, очевидно, являются особыми.
Вообще всегда при интегрировании дифференциального уравнения нужно иметь в виду следующее замечание Н. М. Гюнтера: «Внимательно относясь к процессу, переводящему дифференциальное уравнение в его общий интеграл, можно без всяких интегрирований найти все особые решения, ни одного не пропустив». В дальнейшем будем систематически пользоваться этим указанием для нахождения особых решений всех уравнений, общий интеграл которых удается построить в элементарных функциях или в квадратурах.
Рассмотрим случай полного уравнения (6.3) F(x, y, y’) = 0 , в котором функция F линейно зависит от y и x. Такое уравнение можно, разрешив относительно y, записать в виде
Если φ(y’) ≠ y’, то уравнение (6.4) y = φ(y’)x + ψ(y’) называется уравнением Лагранжа. Найдем его общее решение в параметрической форме.
Воспользуемся основным соотношением:
приняв y’ за параметр, который на этот раз (по традиции) обозначим буквой p (y’ = p). Тогда уравнение Лагранжа (6.4) y = φ(y’)x + ψ(y’) будет равносильно системе двух уравнений

Пользуясь основным соотношением (6.5) dy = y’dx с учетом (6.4, а) 
Это есть дифференциальное уравнение с неизвестной функцией x от независимой переменной p. Замечая, что искомая функция x входит в коэффициент при dp линейно, перепишем его в виде

Это есть линейное уравнение с искомой функцией x. Интегрируя его, получим
Подставляя эту функцию в первое из уравнений (6.4, а) 
Если уравнение φ(p) – p = 0 имеет действительные решения p = pi (i = 1, 2 , …, n), то, подставляя их в первое из уравнений (6.4, а) 
Эти прямые линии могут оказаться особыми решениями уравнения Лагранжа (6.4) y = φ(y’)x + ψ(y’) .
Это уравнение называется уравнением Клеро.
Применяя тот же алгоритм, что и при интегрировании уравнения Лагранжа, имеем
Это уравнение распадается на два:
Первое из них дает p = C = const. Подставляя это значение в первое из уравнений (6.7) y = xp + ψ(p), y’ = p , получим
Это семейство прямых линий и есть общее решение уравнения Клеро (6.6) y = xy’ + ψ(y’) . Заметим, что оно получается из (6.6) y = xy’ + ψ(y’) формальной заменой y’ на C.
Второе из уравнений (6.8) dp = 0 и x + ψ’(p) = 0 вместе с первым из уравнений (6.7) y = xp + ψ(p), y’ = p дает решение уравнения Клеро (6.6) y = xy’ + ψ(y’) в параметрической форме:

которое обычно является особым и представляет наибольший (если не исключительный) интерес для приложений. Геометрически это решение чаще всего является огибающей семейства (6.9) y = xC + ψ(C) и в этом случае представляет собой заведомо особое решение.
Действительно, разыскивая кривую, подозрительную на огибающую семейства (6.9) y = xC + ψ(C) , по правилу, указанному выше, имеем систему
где второе уравнение получено из первого, дифференцированием по C. Из этой системы находим
Но эти уравнения отличаются от (6.10) 
Таким образом, приходим к очень простому алгоритму интегрирования уравнения Клеро:
- Общее решение получается заменой у’ на C.
- Особое решение ищется как огибающая семейства прямых, образующих общее решение.
В случае уравнения Клеро наибольший интерес представляет не общее, а особое решение.
3.7. Уравнение Бернулли.
Рассмотрим одно нелинейное уравнение, которое всегда приводится к линейному. Это уравнение Бернулли:
Для приведения уравнения Бернулли к линейному уравнению избавимся сначала в правой части от множителя y m , разделив на него обе части уравнения. Получим
Это уравнение можно переписать в виде

Введя новую неизвестную функцию z:
придем к уравнению

Это есть линейное уравнение. Найдя его общее решение, получим общее решение уравнения Бернулли по формуле
y = 
Заметим, что если m > 0, то уравнение Бернулли имеет решение y ≡ 0. Это решение будет особым, если 0 (8.2) 
Рассмотрим теперь вопрос о механическом истолковании уравнения второго порядка и его решений. Пусть материальная точка массой m движется по прямой, которую примем за ось x, под действием силы F (t, x, 

m 

где 




где f = 
соответствует, как и в случае уравнения первого порядка, определенный закон движения. Поэтому часто решение (8.5) x = x(t) называют движением, определяемым уравнением (8.5) x = x(t) . Задача, теории интегрирования уравнения (8.4) 



Для уравнения n-го порядка
(n > 1) задача Коши ставится так: найти решение
удовлетворяющее начальным условиям (условиям Коши)
y = y0, y ‘ = 

где x0, y0, 

В частности, для уравнения второго порядка (8.1) F (x, y, y ‘, y ») = 0 начальные условия (8.8) y = y0, y ‘ = 

y = y0, y ‘ = 
Геометрически речь идет о нахождении интегральной кривой y = y(x), проходящей через заданную точку M0 (x0, y0) и имеющей в этой точке касательную M0T, которая образует с положительным направлением оси x заданный угол α0:
tg α0 = 
Наряду с задачей Коши большое значение имеет задача, в которой условия на искомую функцию (и ее производные) налагаются не к одной точке, а на концах некоторого промежутка. Такая задача называется краевой задачей, а налагаемые условия — краевыми условиями.
Теорема существования и единственности решения уравнения n-го порядка
Рассмотрим уравнение n-го порядка в нормальной форме
Для этого уравнения, как и в случае уравнения первого порядка, имеет место следующая теорема существования и единственности решения задачи Коши.
Случай линейного уравнения. Выбор начальных данных. Интервал существования решения
Рассмотрим линейное уравнение n-го порядка
Предположим, что все коэффициенты p1, …, pn и правая часть f (x) заданы и непрерывны в интервале (a, b). Тогда условия сформулированной выше теоремы Пикара заведомо выполняются в окрестности начальной точки (x0, y0, 



Теорема. Если функции p1, …, pn и f (x) непрерывны в интервале (a, b), то уравнение (8.10) y (n) + p1 (x) y (n – 1) + … + pn – 1 (x) y ‘ + pn (x) y = f (x) имеет единственное решение (8.7) y = y(x) , удовлетворяющее начальным условиям (8.8) y = y0, y ‘ = 



Можно доказать, что решение (8.7) y = y(x) определено во всем интервале (а,b).
В частности, если функции p1, …, pn и f (x) — полиномы (или другие функции, непрерывные при всех x), то все начальные данные y0, 

Если функции p1, …, pn, f (x) суть рациональные функции, т. е. являются отношениями полиномов

то при постановке задачи Коши начальные значения y0, 

3.9. Дифференциальные уравнения, допускающие понижение порядка.
Дифференциальное уравнение n-го порядка имеет вид
Если уравнение (9.1) F (x, y, y ‘, …, y (n) ) = 0 разрешимо относительно старшей производной y (n) , то оно примет вид
Рассмотрим некоторые типы уравнений, допускающие понижение порядка.
F (x, y, y ‘, …, y (n) ) = 0,
не содержащее явно неизвестную функцию y.
F (x, y (k) , y (k + 1) , …, y (n) ) = 0,
не содержащее явно неизвестную функцию, а также несколько ее первых производных.
F (x, y, y ‘, …, y (n) ) = 0,
не содержащее явно независимую переменную x.
Например, в дифференциальном уравнении вида F ( y, y ‘, y » ) делается замена y ‘ = z, тогда
y » =
 =
= 
 =
=  z.
z. Заменяя y ‘ = z, y » =
 z, получим дифференциальное уравнение первого порядка
z, получим дифференциальное уравнение первого порядка F
 y, z, y ‘,
y, z, y ‘,  z
z  = 0.
= 0.3.10. Линейные дифференциальные уравнения n-го порядка. Общая теория.
Однородные и неоднородные линейные уравнения n-го порядка
Линейное уравнение n-го порядка имеет следующий общий вид:
и называется однородным. Если f (x) ≠ 0, то уравнение (10.1) y (n) + p1 (x) y (n – 1) + … + pn – 1 (x) y ‘ + pn (x) y = f (x) называется неоднородным. Ниже показано, что, как и в случае линейного уравнения первого порядка, интегрирование неоднородного линейного уравнения (10.1) y (n) + p1 (x) y (n – 1) + … + pn – 1 (x) y ‘ + pn (x) y = f (x) приводится к интегрированию однородного уравнения.
Будем предполагать, что функции p1, …, pn, f (x) непрерывны в интервале (a, b). Это предположение обеспечит существование и единственность решения задачи Коши с любыми y0, 



Понятие о линейном дифференциальном операторе n-го порядка
Таким образом, L(y) есть результат выполнения над функцией y операций, указанных в правой части формулы (10.3) L(y) ≡ y (n) + p1 (x) y (n – 1) + … + pn – 1 (x) y ‘ + pn (x) y , а именно: вычисление производных от функции y вплоть до порядка т включительно, умножение y0, 


L ≡ 


и будем называть его линейным дифференциальным оператором n-го порядка. В частности, линейный дифференциальный оператор второго порядка имеет вид
L ≡ 

Линейный дифференциальный оператор L обладает следующими основными свойствами (линейность оператора L):
1) постоянный множитель можно выносить за знак оператора
2) оператор от суммы двух функций равен сумме операторов от этих функций
Из этих основных свойств оператора L следует, что
L



т. е. оператор от линейной комбинации m функций равен линейной комбинации операторов от этих функций.
Если функция y = y(x) является решением уравнения (10.4) L(y) = f (x) или (10.5) L(y) = 0 в некотором интервале (a, b), то значение оператора L от этой функции равно f (x) или нулю при всех x из (a, b):
Функции cos x и sin x являются действительной и мнимой частями комплексной функции e ix . Так как они определены при всех значениях x, то и функция e ix определена при всех значениях x.
Аналогично определяется показательная функция более общего вида e αx , где α = a + ib; причем a и b — действительные числа:
Здесь действительная и мнимая части e ax cos bx, ie ax sin bx, а вместе с ними и функция e αx определены при всех значениях x.
Введем понятие о производной комплексной функции действительной переменной. Предположим, что действительная и мнимая части комплексной функции (10.6) y(x) = u(x) + iv(x) (i = 
Используя формулу (10.7) y (k) (x) = u (k) (x) + iv (k) (x) , можем вычислить значение оператора L от комплексной функции действительной независимой переменной. При этом получим
т. е. значение оператора L от комплексной функции (10.6) y(x) = u(x) + iv(x) (i = 

Дадим теперь понятие о комплексном решении однородного линейного уравнения L(y) = 0. Функция (10.6) y(x) = u(x) + iv(x) (i = 
откуда вытекает, что

α1, α2, …, αn (a (11.3) α1, α2, …, αn (a однородного линейного уравнения n-го порядка. С этой целью введем в рассмотрение определитель, составленный из данных частных решений и их производных до порядка n – 1 включительно:
W(x) =
Этот определитель называется определителем Вронского решений y1, y2, …, yn.
Теорема. Для того чтобы решения (11.3) α1, α2, …, αn (a были линейно независимы в (a, b), т. е. в интервале непрерывности коэффициентов уравнения L(y) = 0, необходимо и достаточно, чтобы W(x) не обращался в нуль ни в одной точке из (a, b).
Значение определителя Вронского n решений однородного линейного уравнения L(y) = 0 тесно связано с самим уравнением, а именно: имеет место следующая формула Остроградского—Лиувилля:
W(x) = W(x0) 
Из формулы (11.4) W(x) = W(x0) 
- Если W(x) обращается в нуль в одной точке из интервала (a, b), то он равен нулю во всех точках этого интервала.
- Если W(x) не равен нулю в одной точке из интервала (a, b), то он отличен от нуля во всех точках этого интервала.
Таким образом, для того, чтобы n решений (11.3) α1, α2, …, αn (a составляли фундаментальную систему решений уравнения L(y) = 0 в интервале (a, b), достаточно, чтобы их определитель Вронского был отличен от нуля в одной точке x0 ∈ (a, b).
Построение общего решения однородного линейного уравнения по фундаментальной системе решений
Знание фундаментальной системы решений уравнения L(y) = 0 дает возможность построить общее решение этого уравнения.
a (n – 1) | (11.5) a (n – 1) | имеет место существование и единственность решения задачи Коши. Покажем, что функция (11.1) 
1. Система уравнений

разрешима в области (11.5) a (n – 1) | относительно произвольных постоянных C1, C2, …, Cn так как определитель этой системы, будучи равен определителю Вронского для фундаментальной системы решений (11.3) α1, α2, …, αn (a , отличен от нуля.
2. Функция (11.1) 
Поэтому функция (11.1) 
Формула (11.1) 
y = y0, y ‘ = 

где y0, 





относительно произвольных постоянных C1, C2, …, Cn. Так как определитель системы (11.8) 
C1 = 

Подставляя найденные значения произвольных постоянных в общее решение (11.1) 
y = 

Таким образом, фундаментальная система решений (11.3) α1, α2, …, αn (a является базисом n–мерного линейного пространства решений уравнения L(y) = 0.
3.12. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
Рассмотрим линейное уравнение n-го порядка
где коэффициенты a1, a2, …, an суть действительные числа, а правая часть f (x) непрерывна в некотором интервале (a, b) (a ≥ – ∞, b ≤ + ∞).
Так как интегрирование неоднородного линейного уравнения приводится к интегрированию соответствующего однородного уравнения, то рассмотрим сначала вопрос о построении общего решения однородного уравнения
Для нахождения общего решения этого уравнения достаточно знать фундаментальную систему решений. Так как коэффициенты уравнения постоянны и, следовательно, заведомо непрерывны при всех значениях x, то согласно теореме Пикара и все решения уравнения (12.2) L(y) ≡ y (n) + a1 y (n – 1) + … + an – 1 y ‘ + an y = 0 определены при всех значениях x. Поэтому в дальнейшем мы не будем указывать ни интервал существования частных решений, ни область задания общего решения.
Эйлер доказал, что для однородного линейного уравнения с постоянными коэффициентами всегда можно построить фундаментальную систему решений, состоящую из элементарных функций, и, следовательно, это уравнение всегда интегрируется в элементарных функциях. Ниже это утверждение доказывается для уравнения второго порядка и распространяется на уравнение n-го порядка.
Рассмотрим уравнение второго порядка
где p и q — действительные числа. Будем, следуя Эйлеру, искать частное решение уравнения (12.3) L(y) ≡ y » + py ‘ + qy = 0 в виде
где λ — подлежащее определению число (действительное или комплексное). Согласно определению решения функция (12.4) y = e λx будет решением уравнения (12.3) L(y) ≡ y » + py ‘ + qy = 0 , если λ выбрано так, что функция (12.4) y = e λx обращает это уравнение в тождество
Вычисляя L(e λx ), т. е. подставляя функцию (12.4) y = e λx в левую часть уравнения (12.3) L(y) ≡ y » + py ‘ + qy = 0 , и принимая во внимание, что
Из формулы (12.7) L(e λx ) = (λ 2 + pλ + q)e λx следует, что интересующее нас тождество (12.5) L(e λx ) ≡ 0 будет выполняться тогда и только тогда, когда P(λ) = 0, т. е. когда λ является корнем уравнения
Заметим, что характеристическое уравнение (12.8) λ 2 + pλ + q = 0 может быть составлено по данному дифференциальному уравнению (12.3) L(y) ≡ y » + py ‘ + qy = 0 заменой y », y ‘ и y на λ 2 , λ и 1, т. е. степень λ совпадает с порядком производной, если условиться считать, что производная нулевого порядка от функции есть сама функция y (0) ≡ y.
Структура фундаментальной системы решений, а вместе с ней и общего решения уравнения (12.3) L(y) ≡ y » + py ‘ + qy = 0 зависит от вида корней характеристического уравнения (12.8) λ 2 + pλ + q = 0 .
Интегрирование однородного линейного уравнения второго порядка с постоянными коэффициентами в случае различных корней характеристического уравнения
Рассмотрим сначала случаи, когда эти корни различные и действительные. Обозначим их через λ1 и λ2. Тогда, подставляя в формулу (12.4) y = e λx вместо λ числа λ1 и λ2, получим два частных решения уравнения (12.3) L(y) ≡ y » + py ‘ + qy = 0
y1 = 

Эти решения, очевидно, линейно независимы, так как их отношение

не равно тождественно постоянной величине. В линейной независимости решений (12.9) y1 = 

W(x) = 

Следовательно, частные решения y1 = 

y = C1 

Предположим теперь, что корни характеристического уравнения комплексные. Так как коэффициенты этого уравнения действительные, то эти комплексные корни являются сопряженными, так что они имеют вид
Подставляя корень λ1 = a + bi в формулу (12.4) y = e λx , получим комплексное решение
поэтому решение (12.10) y = e (a + bi)x можно записать так:
Отделяя в комплексном решении (12.11) y = e ax cos ax + i e ax sin bx действительную и мнимую части, получим два действительных частных решения
Эти решения, очевидно, независимы, так как

Аналогично убеждаемся, что сопряженному корню λ2 = a – bi соответствуют действительные частные решения
Решения (12.13) e ax cos ax, – e ax sin bx , очевидно, линейно зависимы с решениями (12.12) y1 = e ax cos ax, y2 = e ax sin bx .
Таким образом, паре сопряженных комплексных корней λ1, 2 = a ± bi соответствуют два действительных линейно независимых частных решения (12.12) y1 = e ax cos ax, y2 = e ax sin bx .
Решения (12.12) y1 = e ax cos ax, y2 = e ax sin bx образуют фундаментальную систему решений уравнения (12.3) L(y) ≡ y » + py ‘ + qy = 0 . Поэтому
будет общим решением уравнения (12.3) L(y) ≡ y » + py ‘ + qy = 0 .
Если корни λ1 и λ2 чисто мнимые, т. е. λ1 = ib и λ2 = – ib, то им соответствуют линейно независимые частные решения вида
Эти решения образуют фундаментальную систему решений уравнения (12.3) L(y) ≡ y » + py ‘ + qy = 0 , а
есть общее решение этого уравнения.
Случай кратных корней характеристического уравнения
Предположим теперь, что характеристическое уравнение (12.8) λ 2 + pλ + q = 0 имеет равные корни λ1 = λ2 = – 
y1 = 
y1 = 
Убедимся непосредственной подстановкой в уравнение (12.3) L(y) ≡ y » + py ‘ + qy = 0 в том, что
y2 = x 
есть второе частное решение уравнения (12.3) L(y) ≡ y » + py ‘ + qy = 0 , линейно независимое с решением (12.15) y1 = 








L(x











так как 
Общим решением уравнения (12.3) L(y) ≡ y » + py ‘ + qy = 0 будет
y = 
3.13. Неоднородное линейное дифференциальное уравнение, структура общего решения. Принцип наложения.
Структура общего решения неоднородного линейного уравнения
Покажем, что, как и в случае линейного неоднородного уравнения первого порядка, интегрирование неоднородного уравнения (13.1) L(y) ≡ y (n) + p1 (x) y (n – 1) + … + pn – 1 (x) y ‘ + pn (x) y = f (x) приводится к интегрированию однородного уравнения, если известно одно частное решение неоднородного уравнения (13.1) L(y) ≡ y (n) + p1 (x) y (n – 1) + … + pn – 1 (x) y ‘ + pn (x) y = f (x) .
z = 
Подставляя это значение z в формулу (13.3) y = y1 + z , получим
y = y1 + 
Эта формула содержит в себе все решения неоднородного линейного уравнения (13.1) L(y) ≡ y (n) + p1 (x) y (n – 1) + … + pn – 1 (x) y ‘ + pn (x) y = f (x) . Функция (13.6) y = y1 + 
Таким образом мы доказали следующую теорему о структуре общего решения неоднородного линейного уравнения (13.1) L(y) ≡ y (n) + p1 (x) y (n – 1) + … + pn – 1 (x) y ‘ + pn (x) y = f (x) .
Теорема. Общее решение неоднородного линейного уравнения (13.1) L(y) ≡ y (n) + p1 (x) y (n – 1) + … + pn – 1 (x) y ‘ + pn (x) y = f (x) равно сумме какого-нибудь частного решения этого уравнения и общего решения соответствующего однородного уравнения (13.4) L(z) = 0 .
Общее решение (13.6) y = y1 + 


Задача нахождения частного решения неоднородного уравнения (13.1) L(y) ≡ y (n) + p1 (x) y (n – 1) + … + pn – 1 (x) y ‘ + pn (x) y = f (x) во многих случаях облегчается, если воспользоваться замечательным свойством частных решений, выражаемым следующей теоремой.
и известно, что y1 есть частное решение уравнения
а y2 — частное решение уравнения
3.14. Подбор частных решений линейного неоднородного дифференциального уравнения с постоянными коэффициентами и со специальной правой частью.
Случай для линейного неоднородного дифференциального уравнения с постоянными коэффициентами и с правой частью имеющей вид полинома от x степени m
Для уравнения с постоянными коэффициентами в случае, когда правая часть имеет специальный вид, удается найти частное решение методом неопределенных коэффициентов (методом подбора частных решений).
Рассмотрим этот метод для уравнения n-го порядка вида
где a1, …, an — действительные числа, α — действительное число, Pm (x) — полином от x степени m, которая может быть равной нулю, так что этот полином может вырождаться в число, отличное от нуля.
Метод неопределенных коэффициентов состоит в том, что задается вид частного решения с неопределенными коэффициентами, которые определяются подстановкой в данное уравнение. Вид частного решения уравнения зависит от того, совпадает ли число α с корнями характеристического уравнения:
- Если α не является корнем характеристического уравнения, то частное решение имеет вид
где Qm (x) — полином степени m с коэффициентами, подлежащими определению.
Если α является корнем характеристического уравнения кратности k, то
т. е. частное решение приобретает множитель xk .
Случай для линейного неоднородного дифференциального уравнения с постоянными коэффициентами и с правой частью имеющей вид:
где α и b — действительные числа, P1 и P2 — полиномы от x, старшая степень которых равна m, так что один из них обязательно имеет степень m, а степень другого не превосходит m, и он может быть даже тождественно равен нулю.
Составим комплексное число α + ib, где действительная часть α есть коэффициент показателя множителя e αx , а мнимая часть b — коэффициент аргумента bx функций cos bx и sin bx.
где Q1 и Q2 — полиномы степени m с неопределенными коэффициентами; причем надо брать оба эти полинома даже в том случае, когда один из полиномов P1 и P2 тождественно равен нулю.
Если число α + ib есть корень характеристического уравнения кратности k, то
т. е. частное решение приобретает множитель xk .
3.15. Метод вариации произвольных постоянных.
Пусть дано неоднородное линейное уравнение второго порядка
где коэффициенты p(x), q(x) и правая часть f (x) есть функции от x, непрерывные в некотором интервале (a, b).
Рассмотрим наряду с уравнением (15.1) L(y) ≡ y» + p(x)y’ + q(x)y = f (x) соответствующее ему однородное уравнение
W(x) = 
Тогда, как известно, общее решение уравнения (15.3) L(z1) ≡ 0, L(z2) ≡ 0 имеет вид
Оно содержит производные второго порядка от искомых функций C1(x) и C2(x), так что на первый взгляд задача усложнилась: вместо уравнения второго порядка (15.1) L(y) ≡ y» + p(x)y’ + q(x)y = f (x) с одной неизвестной функцией y мы получили уравнение того же порядка, но уже с двумя неизвестными функциями — C1(x) и C2(x). Однако мы покажем, что искомые функции можно подчинить такому дополнительному условию, что в уравнение (15.6) L(C1(x)z1 + C2(x)z2) = f (x) не войдут производные второго порядка от этих функций.
Дифференцируя обе части равенства (15.5) z = C1(x)z1 + C2(x)z2 , имеем y’ = C1(x) 



Чтобы при вычислении y» не появились производные второго порядка от C1(x) и C2(x), положим


Это и есть то дополнительное условие на искомые функции C1(x) и C2(x), о котором говорилось выше. При этом условии выражение для y’ примет вид
y’ = C1(x) 

Вычисляя теперь y», получим
y» = C1(x) 





Подставим выражения для y, y’ и y» из формул (15.5) z = C1(x)z1 + C2(x)z2 , (15.7) y’ = C1(x) 







C1(x)L(z1) + C1(x)L(z2) + 



Здесь в силу (15.3) L(z1) ≡ 0, L(z2) ≡ 0 первые два слагаемых равны нулю, поэтому




Таким образом мы получили систему дифференциальных уравнений
Эта система в силу (15.4) W(x) = 




где φ1(x) и φ2(x) суть вполне определенные функции от x. Их можно найти, например, по правилу Крамера. При этом, так как z1, z2, 


C1(x) = 

y = z1

Полагая здесь C1 = C2 = 0, получим частное решение
y1 = z1

так что формулу (15.9) y = z1

откуда в силу теоремы о структуре общего решения неоднородного линейного уравнения следует, что формула (15.9) y = z1



Изложенный метод вариации произвольных постоянных легко распространяется на уравнение n-го порядка. Пусть дано неоднородное линейное уравнение n-го порядка
где коэффициенты p1 (x), …, pn (x) и правая часть f (x) суть функции от x, непрерывные в некотором интервале (a, b).
Рассмотрим соответствующее однородное уравнение.
Пусть z1, z2, …, zn — фундаментальная система решений этого уравнения. Тогда
z = 
Решение данного неоднородного уравнения ищется в виде
y = 
где функции Ck(x) определяются из системы уравнений
Решая эту систему относительно 

Ck(x) = 
Подставляя найденные значения Ck(x) в формулу (15.11) y = 
y = 


Это и есть общее решение уравнения. Все решения, входящие в формулу (15.12) y = 


Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения первого порядка с примерами решения и образцами выполнения
Обыкновенным дифференциальным уравнением называется уравнение вида
связывающее независимую переменную х, искомую функцию у = у(х) и ее производные у'(х), у»(х), … , 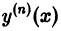
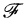
Замечание:
Обозначения зависимой и независимой переменных через х и у, используемые в приведенном определении, не являются жесткими; часто в качестве независимой удобно брать переменную t, иными буквами обозначают и зависимую переменную (см. ниже пример 2).
В обыкновенном дифференциальном уравнении искомая функция у = у(х) есть функция одной независимой переменной x. Если искомая функция есть функция двух (и более) независимых переменных, то имеем дифференциальное уравнение с частными производными. В этой и двух следующих главах мы будем рассматривать только обыкновенные дифференциальные уравнения.
Простейшим дифференциальным уравнением является уравнение вида
где f(x) — известная непрерывная на некотором интервале (а, b) функция, а у = у(х) — искомая функция. С таким уравнением мы уже встречались в интегральном исчислении, когда поданной функции f(x) требовалось найти ее первообразную F(x). Как известно, всякая функция, удовлетворяющая уравнению (2), имеет вид
где F(x) — какая-нибудь первообразная для функции f(x) на интервале (а, Ь), а С — произвольная постоянная. Таким образом, искомая функция у = у(х) определяется из уравнения (2) неоднозначно.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например,
— дифференциальное уравнение 1-го порядка;
— дифференциальное уравнение 2-го порядка;
— дифференциальное уравнение пятого порядка.
Решением дифференциального уравнения n-го порядка на интервале (а, b) называется всякая функция 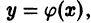
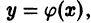
Например, функция у = sin х является решением дифференциального уравнения второго порядка
на интервале 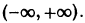
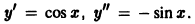
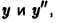
Задача:
Найти совпадающие решения двух дифференциальных уравнений (не решая самих уравнений):
График решения дифференциального уравнения называется интегральной кривой этого уравнения.
Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения. К составлению и интегрированию дифференциальных уравнений приводят многочисленные задачи как самой математики, так и других наук (физики, химии, биологии и т. п.).
Пример:
Найти такую кривую, чтобы тангенс угла наклона касательной в каждой ее точке численно равнялся ординате точки касания.
— уравнение искомой кривой. Как известно, tg а = у'(х) и, значит, определяющее свойство кривой есть
— дифференциальное уравнение первого порядка. Нетрудно видеть, что функция
Есть решение этого уравнения. Оно также имеет очевидное решение у = 0. Кроме того, решениями будут функции
где С — произвольная постоянная, так что уравнение имеет бесконечное множество решений.
Пример:
Найти закон прямолинейного движения материальной точки, движущейся с постоянным ускорением а.
Требуется найти формулу 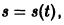
— дифференциальное уравнение второго порядка. Последовательно находим:
Произвольные постоянные можно определить, если положить
В самом деле, полагая t = to в первом из соотношений (*), получаем 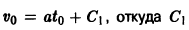
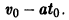
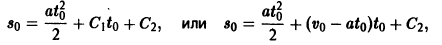
Подставляя найденные значения C1 и С2 в выражение для функции s(t), приходим к известному закону движения материальной точки с постоянным ускорением:
Видео:Решить дифф. уравнение и построить интегральные кривыеСкачать

Эквивалентные дифференциальные уравнения. Задача Коши
Пусть имеем дифференциальное уравнение первого порядка
Если в этом уравнении удается выразить производную у’ через х и у, то получаем уравнение
разрешенное относительно производной. Здесь f — заданная функция своих аргументов.
Наряду с уравнением (1) рассматривают эквивалентное ему дифференциальное уравнение
или уравнение более общего вида
получаемое из (1′) путем умножения на некоторую функцию 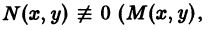
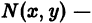
Два дифференциальных уравнения
называются эквивалентными в некоторой области D изменения величин х, у, у’, если всякое решение 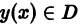
Если дифференциальное уравнение имеет решение, то, как правило, множество его решений оказывается бесконечным. Впрочем, дифференциальное уравнение
имеет только одно решение
y = х,
вообще не имеет действительных решений.
Чтобы выделить определенное решение уравнения (1), надо задать начальное условие, которое заключается в том, что при некотором значении Xо независимой переменной х заранее дано значение Yo искомой функции у(х):
Геометрически это означает, что задается точка 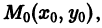
Задачу отыскания решения у(х) уравнения (1), удовлетворяющего начальному условию (2), называют задачей Коши (начальной задачей) для уравнения (1).
Теорема существования и единственности решения задачи Коши для уравнения у’ = f(x, у)
Теорема:
Существования и единственности решения. Пусть имеем дифференциальное уравнение
и пусть функция f(x,y) определена в некоторой области D на плоскости хОу. Выберем произвольную точку 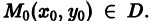
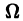
1) непрерывна по совокупности аргументов;
2) имеет ограниченную частную производную 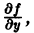
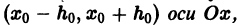
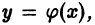
Геометрически это означает, что через точку 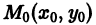
Теорема 1 имеет локальный характер: она гарантирует существование единственного решения 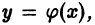
Пример:
у’ = х + у
f(x,y) = x + у
определена и непрерывна во всех точках плоскости хОу и имеет всюду 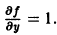
Пример:
определена и непрерывна на всей плоскости хОу. Здесь
так что второе условие теоремы 1 нарушается в точках оси Ох. Нетрудно проверить, что функция
где С — любая постоянная, является решением данного уравнения. Кроме того, уравнение имеет очевидное решение
Если искать решения этого уравнения, соответствующие условию у(0) = 0, то таких решений найдется бесчисленное множество, а частности, следующие (рис. 2):
Таким образом, через каждую точку оси Ох проходят по крайней мере две интегральные кривые и, следовательно, в точках Этой оси нарушается единственность.
Если взять точку М1 (1,1), то в достаточно малой ее окрестности выполнены все условия теоремы 1. Следовательно, через данную точку в малом квадрате 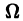
уравнения 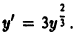
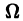
Теорема 1 дает достаточные условия существования единственного решения уравнения у’ = f(x,y). Это означает, что может существовать единственное решение у = у(х) уравнения у’ = f(x, у), удовлетворяющее условию 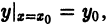
Пример:
В точках оси Ох функции 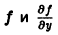
Но через каждую точку (Хо, 0) оси Ох проходит единственная интегральная кривая
Замечание:
Если отказаться от ограниченности 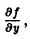
Теорема:
Если функция f(x, у) непрерывна в некоторой окрестности точки (х0, уо), то уравнение у’ = f(x, у) имеет в этой окрестности по крайней мере одно решение 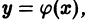
Задача:
Найти интегральную кривую уравнения
проходящую через точку О (0,0).
Задача:
Найти решение задачи Коши
Определение:
Общим решением дифференциального уравнения
в некоторой области 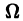
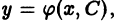
1) при любом допустимом значении постоянной С функция 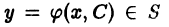
2) каково бы ни было начальное условие 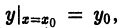
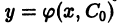
При этом предполагается, что точка (Хо, Уо) принадлежит области 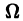
Пример:
Показать, что общим решением дифференциального уравнения
у’ = 1
у = х + С,
где С — произвольная постоянная.
В данном случае f(x, у) = 1, и условия теоремы 1 выполняются всюду. Следовательно, через каждую точку (Хо, Уо) плоскости хОу проходит единственная интегральная кривая данного уравнения.
Проверим, что функция
у = х + С
удовлетворяет условиям 1) и 2), содержащимся в определении общего решения. Действительно, при любом С имеем
у’ = (х + С)’ = 1,
так что у = х + С есть решение данного уравнения. Потребовав, чтобы при Х = Хо решение принимало значение Уо, приходим к соотношению Уо = Хо + Со. откуда
Решение у = х + Уо — Хо, или
удовлетворяет поставленному начальному условию.
Частным решением дифференциального уравнения (1) называется решение, получаемое из общего при каком-либо конкретном значении произвольной постоянной С (включая 
В процессе интегрирования дифференциального уравнения мы часто приходим к уравнению
неявно задающему общее решение уравнения. Уравнение (2) называют общим интегралом дифференциального уравнения (1).
где 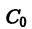
Замечание:
Название происходит от того, что для простейшего дифференциального уравнения вида
его общее решение действительно записывается при помощи обычного неопределенного интеграла
Пример:
Общий интеграл уравнения
имеет следующий вид
В дальнейшем для краткости мы будем иногда говорить, что решение уравнения проходит через некоторую точку 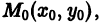
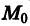
Определение:
дифференциального уравнения (1) называется особым, если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку 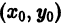
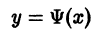
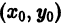
График особого решения называют особой интегральной кривой уравнения. Геометрически это — огибающая семейства интегральных кривых дифференциального уравнения, определяемых его общим интегралом.
Если для дифференциального уравнения (1) в некоторой области D на плоскости хОу выполнены условия теоремы 1, то через каждую точку 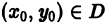
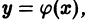
образующих общий интеграл уравнения (1), и получается из этого семейства при конкретном значении параметра С, т.е. является частным интегралом уравнения (1). Никаких других решений, проходящих через точку 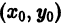
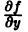
Напомним, что огибающей семейства кривых 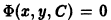
Например, для уравнения
функция 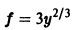
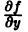
— семейство кубических парабол — и очевидное решение
проходящее через те точки, где производная 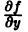
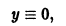
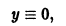
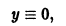
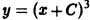

Из теоремы 1 можно вывести только необходимые условия для особого решения. Множество тех точек, где производная 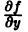
то в точках прямой у = 0 по-прежнему нарушается условие ограниченности производной 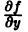
Итак, чтобы найти особые решения уравнения (1), надо
1) найти множество точек, где производная 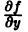
2) если это множество точек образует одну или несколько кривых, проверить, являются ли они интегральными кривыми уравнения (1);
3) если это интегральные кривые, проверить, нарушается ли в каждой их точке свойство единственности.
При выполнении всех этих условий найденная кривая представляет собой особое решение уравнения (1).
Задача:
Найти особые решения уравнения
Видео:12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать

Приближенные методы интегрирования уравнения у’ = f(x, у)
Метод изоклин
Пусть имеем дифференциальное уравнение
где функция f(x, у) в некоторой области D на плоскости хОу удовлетворяет условиям теоремы 1. Это уравнение определяет в каждой точке (х, у) области D значение у’, т. е. угловой коэффициент касательной к интегральной кривой в этой точке. Говорят, что уравнение (1) определяет в области D поле направлений. Чтобы его построить, надо в каждой точке 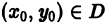
Совокупность этих отрезков дает геометрическую картину поля направлений. Задача интегрирования дифференциального уравнения (1) может быть теперь сформулирована так: найти такую кривую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке. Такое истолкование дифференциального уравнения и его интегрирования дает графический способ решения уравнения.
Для построения интегральных кривых пользуются изоклинами. Изоклиной называется множество всех точек плоскости хОу, в которых касательные к искомым интегральным кривым имеют одно и то же направление (у’ = const).
Из этого определения следует, что семейство изоклин дифференциального уравнения (1) задается уравнением
где к — числовой параметр. Если придать параметру к близкие числовые значения, можно найти достаточно густую сеть изоклин и приближенно построить интегральные кривые дифференциального уравнения.
Пример:
по способу изоклин.
Семейство изоклин данного уравнения определяется уравнением
Полагая к = 0, + 1, — 1,…, получаем изоклины
по которым строим интегральные кривые уравнения (рис. 4).
определяет множество возможных точек экстремума интегральных кривых (прямая x = 0 в примере 1).
Для большей точности построения интегральных кривых определяют направление вогнутости и точки перегиба этих кривых (если такие точки существуют). Для этого находят у» в силу уравнения (1):
Знак правой части определяет знак у», т. е. направление вогнутости интегральных кривых. Линия, заданная уравнением
есть множество всех возможных точек перегиба интегральных кривых.
В примере 1 имеем
поэтому все интегральные кривые обращены вогнутостью вверх, и точек перегиба интегральных кривых нет.
Метод последовательных приближений
Пусть имеем дифференциальное уравнение
где функция f(x, у) в некоторой области D изменения х, у удовлетворяет условиям теоремы 1, и пусть точка 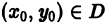
равносильно решению некоторого интегрального уравнения, т. е. уравнения, в которое неизвестная функция входит под знаком интеграла. В самом деле, пусть
— решение уравнения (2), заданное в некоторой окрестности 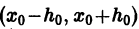
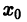
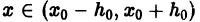
Проинтегрируем это тождество по х
Отсюда учитывая (3), получаем
так что решение у(х) задачи Коши удовлетворяет интефальному уравнению
Обратно: если непрерывная функция 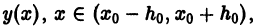
Решение 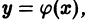
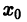
причем в качестве 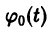
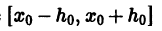
Пример:
Методом последовательных приближений решить задачу Коши
Сводим данную задачу к интегральному уравнению
Выбирая за нулевое приближение функцию
Легко видеть, что функция 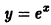
Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Численные методы решения задачи Коши Метод Эйлера
Пусть требуется найти приближенное решение дифференциального уравнения
удовлетворяющее начальному условию
Будем предполагать, что в некотором прямоугольнике 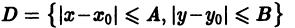
Численное решение задачи (1)-(2) состоит в построении таблицы приближенных значений 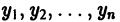
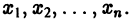
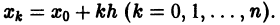
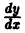
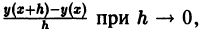
Отсюда последовательно находим значения 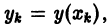
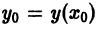
В результате вместо решения у = у(х) мы находим функцию
дискретного аргумента 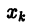
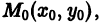
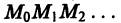
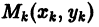
Метод Эйлера относится к группе одно-шаговых методов, в которых для вычисления точки 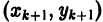
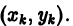
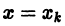
Сравнение формул (4) и (5) показывает, что они совпадают до членов первого порядка по h включительно, а погрешность формулы (4) равна 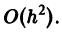
Пример:
Методом Эйлера решить задачу Коши
на отрезке |0; 0,5] с шагом h = 0,1.
В данном случае 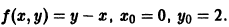
и т. д. Результаты вычислений сведем в таблицу
Замечание:
Если рассмотреть задачу Коши
на любом отрезке [0, a] с любым шагом h > 0, то получим 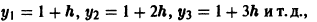
Видео:Практика 1 ИзоклиныСкачать

Понятие о методе Рунге—Кутта
Метод Эйлера весьма прост, но имеет низкую точность. Точность решения можно повысить путем усложнения разностной схемы. Весьма распространенными на практике являются схемы Рунге—Кутта.
Пусть опять требуется решить задачу Коши (1)-(2). Будем строить таблицу приближенных значений 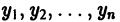
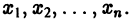
Рассмотрим схему равноотстоящих узлов 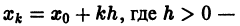
Видео:11. Уравнения в полных дифференциалахСкачать

Некоторые виды уравнений, интегрируемых в квадратурах
В общем случае, даже зная, что решение уравнения существует, отыскать его довольно трудно. Однако существуют некоторые виды дифференциальных уравнений, методы получения решений которых особенно просты (при помощи интегралов от элементарных функций). Рассмотрим некоторые из них.
Уравнения с разделяющимися переменными
называется дифференциальным уравнением с разделенными переменными. Здесь f1(y), f2(x) — известные непрерывные функции своих аргументов.
Покажем, как найти решение этого уравнения. Пусть 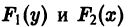
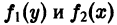
Отсюда следует, что
где С — произвольная постоянная.
Разрешая последнее уравнение (2) относительно у, получим функцию (может быть, и не одну)
которая обращает уравнение (1) в тождество и значит, является его решением.
— уравнение с разделенными переменными. Записав его в виде
и интегрируя обе части, найдем общий интеграл данного уравнения:
в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от x и только от у, называется дифференциальным уравнением с разделяющимися переменными, так как путем деления на 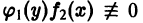
Пример:
Деля обе част уравнения на 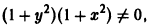
Интегрируя обе части полученного равенства, найдем
Заметим, что деление на 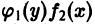
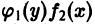
Например, разделяя переменные в уравнении
а после интегрирования —
(здесь С может принимать как положительные, так и отрицательные значения, но 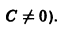
которое может быть включено в общее решение у = Сх, если постоянной С разрешить принимать значение С = 0.
Если считать переменные х и у равноправными, то уравнение
теряющее смысл при х = 0, надо дополнить уравнением
которое имеет очевидное решение х = 0.
В общем случае наряду с дифференциальным уравнением
следует рассматривать уравнение
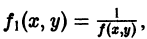
Некоторые дифференциальные уравнения путем замены переменных могут быть приведены к уравнениям с разделяющимися переменными. Например, уравнение вида
где f(x) — непрерывная функция своего аргумента, a, b, с — постоянные числа, подстановкой z = ах + by + с преобразуется в дифференциальное уравнение с разделяющимися переменными:
После интегрирования получаем
Заменяя в последнем соотношении z на ах + by + с, найдем общий интеграл уравнения (5).
Пример:
Положим z = x + y, тогда
Интегрируя, находим или
Подставляя вместо z величину х + у, получаем общее решение данного уравнения
Пример:
Известно, что скорость радиоактивного распада пропорциональна количеству х еще не распавшегося вещества. Найти зависимость х от времени t, если в начальный момент 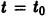
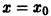
Дифференциальное уравнение процесса
Здесь к > 0 — постоянная распада — предполагается известной, знак «-» указывает на уменьшение х при возрастании t. Разделяя переменные в уравнении (») и интегрируя, получаем
Учитывая начальное условие 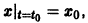
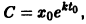
Любой процесс (не только радиоактивный распад), при котором скорость распада пропорциональна количеству еще не прореагировавшего вещества, описывается уравнением (*). Уравнение
отличающееся лишь знаком правой части от уравнения (*), описывает лавинообразный процесс размножения, например «размножение» нейтронов в цепных ядерных реакциях или размножение бактерий в предположении, что скорость их размножения пропорциональна наличному числу бактерий. Решение уравнения (»»»), удовлетворяющее условию 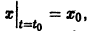
и в отличие от решения уравнения (**) возрастает с возрастанием t. Уравнения (*) и (***) можно объединить в одно
которое дает простейшую математическую модель динамики популяций (совокупности особей того или иного вида растительных или животных Организмов). Пусть y(t) — число членов популяции в момент времени t. Если предположить, что скорость изменения популяции пропорциональна величине популяции, то мы приходим к уравнению (****). Положим k=m-n, где m — коэффициент относительной скорости рождаемости, a n — коэффициент относительной скорости умирания. Тогда к > 0 при m > n и k
при к 
Уравнение динамики популяции в этой модели имеет вид
Это так называемое логистическое уравнение — фундаментальное уравнение в демографии и в математической теории экологии. Оно применяется в математической теории распространения слухов, болезней и других проблемах физиологии и социологии. Разделяя переменные в последнем уравнении, получаем
и выражая у через t, окончательно получаем
Считая, что 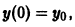
При а > 0 и А > 0 получаем, что 
Уравнения, однородные относительно x и у
Функция f(x, у) называется однородной функцией n-го измерения относительно переменных х и у, если при любом допустимом t справедливо тождество
Например, для функции
так что 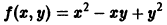
так что 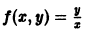
называется однородным относительно х и у, если функция f(x, у) есть однородная функция нулевого измерения относительно переменных х и у.
Пусть имеем дифференциальное уравнение
однородное относительно переменных х и у. Положив 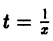
т. е. однородная функция нулевого измерения зависит только от отношения аргументов. Обозначая 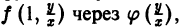
При произвольной непрерывной функции 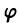
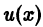
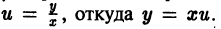
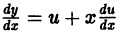
Деля обе части последнего равенства на 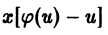
Заменяя здесь и на его значение 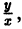
Пример:
Положим 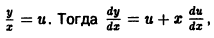
Интегрируя, найдем 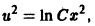
Пример:
Найти форму зеркала, собирающего пучок параллельно падающих на него лучей в одну точку.
Прежде всего, зеркало должно иметь форму поверхности вращения, так как только для поверхности вращения все нормали к поверхности проходят через ось вращения.
Выберем прямоугольную декартову систему координат так, чтобы лучи были параллельны оси Ох и чтобы точкой, в которой собирались бы отраженные лучи, явилось бы начало координат. Найдем форму сечения зеркала плоскостью хОу. Пусть уравнение сечения есть 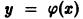
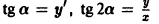
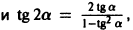
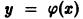
— дифференциальное уравнение, определяющее требуемый ход луча. Разрешая это уравнение относительно производной, получаем два однородных уравнения:
Первое из них путем замены 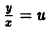
Потенцируя последнее соотношение и заменяя и через 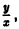
Полученное уравнение в плоскости хОу определяет семейство парабол, симметричных относительно оси Ох. фокусы всех этих парабол совпадают с началом координат. Фиксируя С и вращая параболу вокруг оси Ох, получаем параболоид вращения
Таким образом, зеркало в виде параболоида вращения решает поставленную задачу. Это свойство используется в прожекторах.
Замечание:
то уравнение (6) имеет вид
и интегрируется разделением переменных. Его общее решение
Если 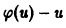
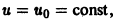
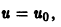
(прямая, проходящая через начало координат).
Рассмотрим уравнения, приводящиеся к однородным. Уравнение
где 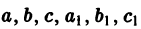
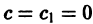
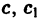
- Определитель
отличен от нуля. Введем новые переменные
по формулам
где h и k — пока не определенные постоянные. Тогда 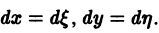
Если выбрать h и k как решения системы линейных алгебраических уравнений
то получим однородное относительно 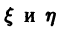
Заменяя в его общем интеграле 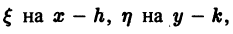
2. Определитель 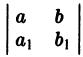
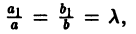
и приводится к уравнению с разделяющимися переменными подстановкой z = ax+by. Аналогичными приемами интегрируется уравнение
где f(w) — непрерывная функция своего аргумента.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Линейные дифференциальные уравнения
Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной. В общем случае оно имеет вид
где коэффициенты уравнения А(х) и В(х) и его правая часть f(x) считаются известными функциями, заданными на некотором интервале
Если 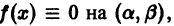
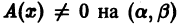
Теорема:
Если функции р(х) и q(x) непрерывны на отрезке 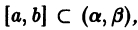
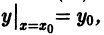
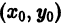
Разрешая уравнение (10) относительно у’, приведем его к виду
где правая часть
удовлетворяет всем условиям теоремы 1: она непрерывна по совокупности переменных х и у и имеет ограниченную частную производную
в указанной полосе. Отсюда следует справедливость утверждения.
Линейное однородное уравнение, соответствующее уравнению (10), имеет вид
Оно интегрируется разделением переменных:
При делении на у потеряно решение 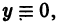
Для интегрирования неоднородного линейного уравнения
может быть применен так называемый метод вариации постоянной. Он основан на том, что общее решение уравнения (10) равно сумме общего решения уравнения (11) и какого-либо частного решения уравнения (10)
Подставляя в левую часть (11) вместо у сумму 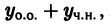
С другой стороны, разность двух частных решений 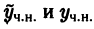
Поэтому сначала интегрируем соответствующее однородное уравнение
общее решение которого имеет вид
где С — произвольная постоянная. Решение неоднородного уравнения (10) ищем в виде
где С(х) — новая неизвестная функция.
Вычисляя производную 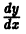
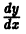
где С — новая произвольная постоянная интегрирования. Следовательно,
Это есть общее решение линейного неоднородного дифференциального уравнения (10).
В формуле (14) общего решения неопределенные интегралы можно заменить определенными интегралами с переменным верхним пределом:
Здесь 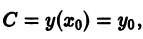
где роль произвольной постоянной играет начальное значение 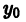
Формула (15) является общим решением уравнения (10) в форме Коши. Отсюда следует, что если р(х) и q(х) определены и непрерывны в интервале 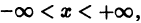
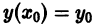
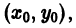
Пример:
соответствующее данному, проинтегрируем, разделяя переменные:
Решение исходного уравнения будем искать в виде
где С(х) — неизвестная функция. Находя 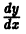
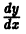
где С — постоянная интегрирования. Из формулы (**) находим общее решение уравнения (*)
Частное решение 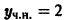
Пример:
Рассмотрим дифференциальное уравнение, описывающее изменение силы тока при замыкании цепи постоянного электрического тока.
Если R — сопротивление цепи, Е — внешняя ЭДС, то сила тока I = I(t) постепенно возрастает от значения, равного нулю, до конечного стационарного значения
Пусть L — коэффициент самоиндукции цепи, роль которой такова, что при всяком изменении силы тока в цепи появляется электродвижущая сила, равная 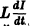
Уравнение (*) есть линейное неоднородное уравнение относительно I(t). Нетрудно видеть, что его частным решением является функция
Общее решение соответствующего однородного уравнения
откуда общее решение неоднородного уравнения (*):
При t = 0 имеем I(0) = 0, поэтому 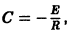
Отсюда видно, что сила тока при включении асимптотически приближается при 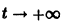
Линейное неоднородное дифференциальное уравнение
может быть проинтегрировано также следующим приемом. Будем искать решение у(х) уравнения (10) в виде
где 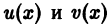
Выберем в качестве v(x) любое частное решение 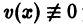
Тогда в силу (17) для u(х) получим уравнение
которое без труда интегрируется в квадратурах. Зная 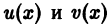
Пример:
Найти общее решение уравнения
Будем искать решение у(х) данного линейного неоднородного уравнения в виде
Подставляя 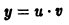
Определим функцию v(x) как решение уравнения
Разделяя переменные, найдем
Выберем любое частное решение, например, отвечающее С = 1. Тогда из (17′) получим
откуда
Для общего решения исходного уравнения получаем выражение
Преимущество метода вариации постоянной заключается в том, что он переносится на линейные неоднородные дифференциальные уравнения высшего порядка.
Уравнение Бернулли
Некоторые дифференциальные уравнения путем замены переменных могут быть сведены к линейным. К числу таких уравнений относится уравнение Бернулли
Уравнение это предложено Я. Бернулли в 1695 г., метод решения опубликовал И. Бернулли в 1697 г.
При а = 1 получаем однородное линейное уравнение
При а = 0 — неоднородное линейное уравнение
Поэтому будем предполагать, что 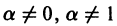
Подстановкой 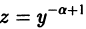
Однако уравнение Бернулли можно проинтегрировать сразу методом вариации постоянной. Это делается так. Сначала интегрируем уравнение
Его общее решение
Решение уравнения Бернулли будем искать в виде
где С(х) — новая неизвестная функция. Подставляя это выражение для у(х) в уравнение Бернулли, получаем
— уравнение с разделяющимися переменными относительно С(х). Интегрируя это уравнение,находим
где С — постоянная интегрирования. Тогда из формулы (*) получаем общий интеграл уравнения Бернулли
Замечание:
При а > 0 уравнение Бернулли имеет очевидное решение
Для интегрирования уравнения Бернулли
можно также воспользоваться подстановкой
где в качестве v(x) берется любое нетривиальное решение уравнения
а функция u(х) определяется как решение уравнения
Пример:
Найти решение уравнения Бернулли
Ищем решение у(х) уравнения в виде
Подставляя 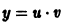
Выберем в качестве v(x) какое-нибудь ненулевое решение уравнения
и проинтегрируем его,
Поскольку нас интересует какое угодно частное решение, положим С = 1, т.е. возьмем 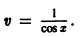
интегрируя которое, найдем
Общее решение у(х) исходного уравнения определится формулой
Уравнения в полных дифференциалах
называется уравнением в полных дифференциалах, если левая часть уравнения представляет собой полный дифференциал некоторой функции u(х, у) двух независимых переменных х и у, т. е.
В этом случае u(х, у) = С будет общим интегралом дифференциального уравнения (18).
Будем предполагать, что функции М(х, у) и N(x, у) имеют непрерывные частные производные соответственно по у и по x в некоторой односвязной области D на плоскости хОу.
Теорема:
Для того чтобы левая часть М(х, у) dx + N(x, у) dy уравнения (18) была полным дифференциалом некоторой функции и(х, у) двух независимых переменных х и у, необходимо и достаточно, чтобы выполнялось тождество
Необходимость:
Предположим, что левая часть уравнения (18) есть полный дифференциал некоторой функции u(х, у), т. е.
тогда 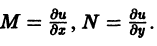
Отсюда, в силу равенства смешанных производных, вытекает тождество
Необходимость (19) доказана.
Достаточность:
Покажем, что условие (19) является и достаточным, а именно, предполагая его выполненным, найдем функцию u(х, у) такую, что du = M(x, у) dx + N(x, у) dy, или, что то же,
Найдем сначала функцию u(х, у), удовлетворяющую первому условию (20). Интегрируя это равенство по х (считаем у постоянной), получаем
где 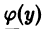
Подберем 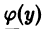
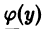
Приравняв правую часть полученного равенства к N(x, у), найдем
Левая часть последнего равенства не зависит от x. Убедимся в том, что при условии (20) в его правую часть также не входит х. Для этого покажем, что частная производная по x от правой части (22) тождественно равна нулю. Имеем
Теперь, интегрируя равенство (22) по у, получим, что
где С — постоянная интегрирования. Подставляя найденное значение для 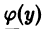
полный дифференциал которой, как нетрудно проверить, равен
Приведенный прием построения функции u(х, у) составляет метод интегрирования уравнения (18), левая часть которого есть полный дифференциал.
Пример:
Проверить, что уравнение
является уравнением в полных дифференциалах, и проинтегрировать его.
В данном случае
Следовательно, уравнение (*) есть уравнение в полных дифференциалах. Теперь находим и (см. (21)):
Находя 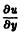
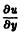
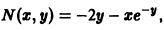
откуда 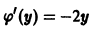
Подставив найденное выражение для 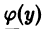
— общий интеграл исходного уравнения.
Иногда можно найти такую функцию 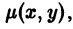
будет полным дифференциалом, хотя М dx + N dy может им и не быть. Такую функцию 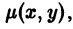
при определенных условиях на функции М(х, y) и N(x, у) интегрирующий множитель всегда существует, но отыскание его из условия
в общем случае сводится к интегрированию уравнения в частных производных, что составляет, как правило, задачу еще более трудную.
Задача:
Найти интегрирующий множитель для линейного дифференциального уравнения
Указание. Искать множитель в виде
Уравнение Риккати
где q(x), р(х), г(х) — известные функции, называется уравнением Риккати. Если р, q, г — постоянные, то оно интегрируется разделением переменных:
В случае, когда 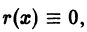
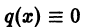
Укажем некоторые свойства уравнения Риккати.
Теорема:
Если известно одно частное решение уравнения Риккати, то его общее решение может быть получено с помощью квадратур.
Пусть известно частное решение 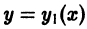
Полагая 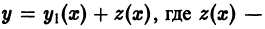
— уравнение Бернулли, которое интегрируется в квадратурах.
Пример:
Проинтегрировать уравнение Риккати
если известно его частное решение
для функции z(x) получаем
решением исходного уравнения будет функция
Частным случаем уравнения (1) является специальное уравнение Риккати:
где a, b, а — постоянные. При а = 0 имеем
и уравнение интегрируется разделением переменных.
При а = -2 получаем
Полагая 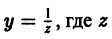
Это уравнение однородное относительно х, z. Оно интегрируется в квадратурах.
Кроме а = 0 и а = -2 существует еще бесконечное множество других значений а, при которых уравнение Риккати (3) интегрируется в квадратурах. Они задаются формулой
При всех других значениях а решение уравнения Риккати (3) не выражается в квадратурах.
Замечание. Если же положить в уравнении (3)
где u = u(x) — новая неизвестная функция, то придем к уравнению второго порядка
решение которого может быть выражено в функциях Бесселя.
Видео:4. Однородные дифференциальные уравнения (часть 1)Скачать

Дифференциальные уравнения, не разрешенные относительно производной
Рассмотрим теперь общий случай уравнения первого порядка
не разрешенного относительно производной.
Уравнения, относящиеся к этому классу, весьма разнообразны, и поэтому в общем случае становится невозможным делать выводы о существовании и единственности решения, даже накладывая достаточно сильные ограничения на участвующие в уравнении функции (ограниченность, гладкость, монотонность и т. п.). Например, уравнение
вообще не имеет действительных решений. Для уравнения
решения суть прямые 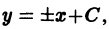
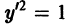
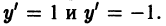
удается разрешить относительно производной у’, то получаются уравнения вида
которые иногда могут быть проинтегрированы изложенными выше методами.
Введем понятие общего решения (интеграла) для уравнения (1). Допустим, что это уравнение в окрестности точки 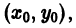
и пусть каждое из этих уравнений имеет общее решение
или общий интеграл
Совокупность общих решений (2) (или общих интегралов (3)) будем называть общим решением (общим интегралом) уравнения (1). Так, уравнение
распадается на два:
Их общие решения у = х + С, у = -х + С в совокупности составляют общее решение исходного уравнения 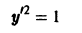
Однако не всегда уравнение (1) легко разрешимо относительно у’ и еще реже полученные после этого уравнения 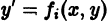
Пусть уравнение (1) имеет вид
причем существует по крайней мере один действительный корень 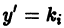
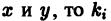
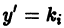
Но 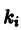
— интеграл рассматриваемого уравнения.
2. Пусть уравнение (1) имеет вид
Если это уравнение трудно разрешить относительно у’, то бывает целесообразно ввести параметр t и заменить уравнение (5) двумя:
Следовательно, искомые интегральные кривые определяются уравнениями в параметрической форме
Пример:
Полагаем,
и параметрические уравнения искомых интегральных кривых:
Если уравнение (5) легко разрешимо относительно у, то обычно за параметр берут у’. Действительно, если 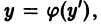
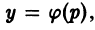
Параметрические уравнения интефальных кривых:
Исключая параметр р, получаем общий интеграл
Пример:
Разрешим уравнение относительно у:
Положим у’ = р, тогда
Таким образом, находим параметрические уравнения интегральных кривых
Параметр р здесь легко исключить. В самом деле, из первого уравнения системы находим
Первую часть второго уравнения преобразуем следующим образом:
— общее решение данного дифференциального уравнения.
3. Пусть уравнение (1) имеет вид
Если это уравнение трудно разрешить относительно у’, то, как и в предыдущем случае, целесообразно ввести параметр t и заменить уравнение (6) двумя:
Следовательно, интегральные кривые уравнения (6) определяются в параметрической форме уравнениями
Если уравнение (6) легко разрешимо относительно х:
то в качестве параметра удобно выбрать 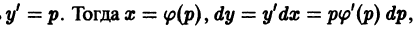
Пример:
Положим у’ = р. Тогда
В параметрической форме семейство интегральных кривых данного уравнения определяют уравнения
Уравнение Лагранжа
Уравнением Лагранжа называется дифференциальное уравнение вида
линейное относительно х и у. Здесь 
Введя параметр 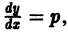
— соотношение, связывающее переменные х, у и параметр р. Чтобы получить второе соотношение, нужное для определения х и у как функций параметра р, продифференцируем (8) по х:
Уравнение (10) линейно относительно х и 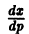
уравнения (10) и присоединив к нему уравнение
получим параметрические уравнения искомых интегральных кривых.
При переходе от уравнения (9) к (10) пришлось делить на 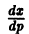
Считая р постоянным, замечаем, что уравнение (9) удовлетворяется лишь в том случае, если р является корнем уравнения
Итак, если уравнение 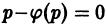
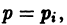
— это прямые линии.
Уравнение Клеро
Уравнением Клеро называется дифференциальное уравнение вида
Полагая у’ = р, получаем
Дифференцируя по х, имеем
откуда или 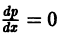
В первом случае, исключая р, найдем семейство прямых
— общее решение уравнения Клеро. Оно находится без квадратур и представляет собой однопараметрическое семейство прямых. Во втором случае решение определяется уравнениями
Можно показать, что, как правило, интегральная кривая (12) является огибающей найденного семейства прямых.
Пример:
Решить уравнение Клеро
Общее решение данного уравнения видно сразу:
Другое (особое) решение определяется уравнениями
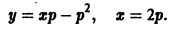
Исключая параметр р, находим
— огибающую прямых
Для уравнения вида
через некоторую точку 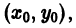
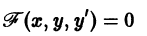
и если каждое из уравнений 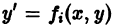
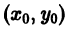
Поэтому свойство единственности решения уравнения 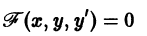
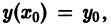
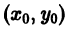
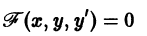
Например, для решений уравнения
свойство единственности в этом смысле всюду выполнено, поскольку через каждую точку 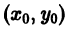
(см. пример 4) через точку (0,0) проходят также две интегральные линии: прямая
входящая в общее решение этого уравнения, и парабола
причем эти линии имеют в точке (0,0) одно и то же направление:
Таким образом, в точке (0,0) свойство единственности нарушается.
Теорема:
Пусть имеем уравнение
и пусть в некоторой окрестности точки 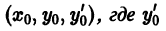
функция 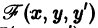
1) 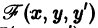
2) производная 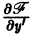
3) существует ограниченная производная
Тогда найдется отрезок 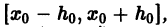
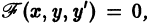
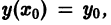
Геометрические вопросы, связанные с дифференциальными уравнениями 1-го порядка. Ортогональные траектории
Общее решение 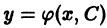
Поставим теперь в некотором смысле обратную задачу: дано однопараметрическое семейство кривых
и требуется составить дифференциальное уравнение, для которого 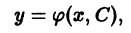
Итак, пусть дано соотношение
где С — параметр. Дифференцируя (1) по х, получим
Если правая часть (2) уже не содержит С, то формула (2) будет представлять дифференциальное уравнение семейства кривых (1). Например, если 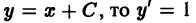
Пусть теперь правая часть (2) содержит С. Разрешая соотношение (1) относительно С, определим С как функцию х и у:
Подставляя это выражение для С в формулу (2), получим дифференциальное уравнение 1-го порядка
Нетрудно убедиться в том, что 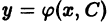
Если соотношение между величинами х, у и С задано в виде
то, дифференцируя его по х, получим
Исключая С из соотношений (5) и (6), приходим к уравнению
Можно показать, что (5) является общим интегралом уравнения (7).
Ортогональные траектории
В ряде прикладных вопросов встречается следующая задача. Дано семейство кривых
Требуется найти такое семейство
чтобы каждая кривая семейства Ф(х, у, С) = 0, проходящая через точку (х, у), пересекалась в этой точке кривой семейства 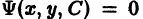
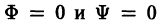
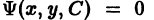
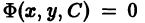
Аналитически это означает следующее. Если
есть дифференциальное уравнение семейства
то дифференциальное уравнение траекторий, ортогональных к семейству Ф = 0, имеет вид
(угловые коэффициенты касательных к кривым семейств 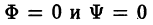
Таким образом, чтобы найти ортогональные траектории к семейству 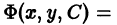
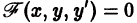
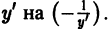
Пример:
Найти ортогональные траектории семейства
окружностей с центром в начале координат.
Составляем дифференциальное уравнение семейства (8). Дифференцируя (8) по х, получим
Это дифференциальное уравнение данного семейства. Заменив в нем 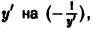
Интегрируя последнее уравнение, получаем, что искомыми ортогональными траекториями будут полупрямые (рис. 9)
Видео:Дифференциальные уравнения. 11 класс.Скачать

Дополнение к дифференциальным уравнениям первого порядка







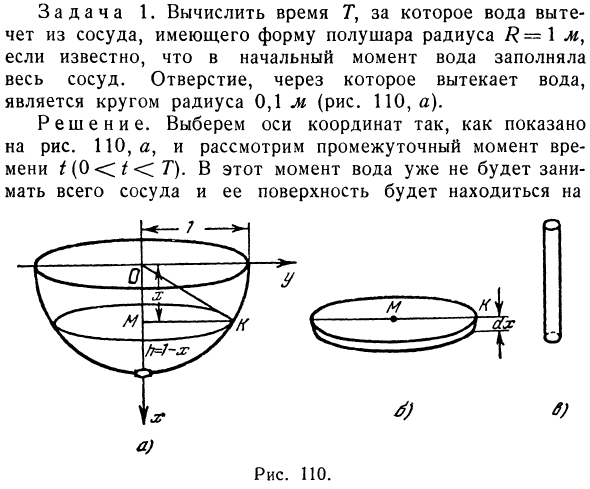



Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
📺 Видео
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Поле направлений дифференциального уравнения первого порядкаСкачать

Как написать уравнения касательной и нормали | МатематикаСкачать

6. Особые решения ДУ первого порядкаСкачать

1. Что такое дифференциальное уравнение?Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Построить интегральную кривуюСкачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Общее и частное решение дифференциального уравненияСкачать







 = u, где u = u(x).
= u, где u = u(x).







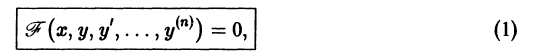

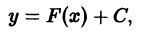
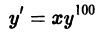
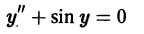
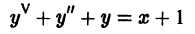
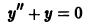
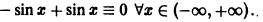
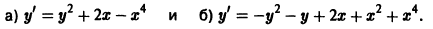
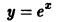
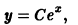
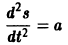
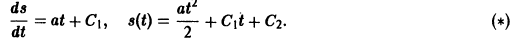
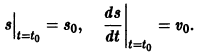

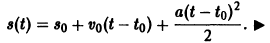

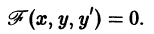


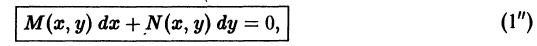
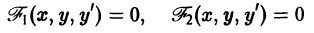
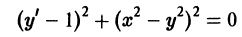
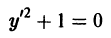
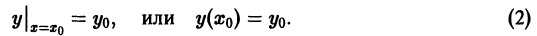

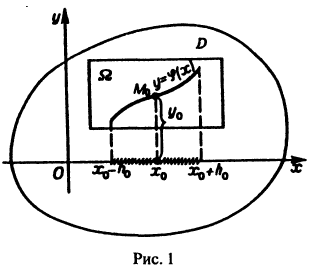
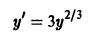
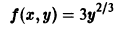
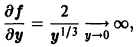
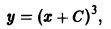
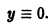
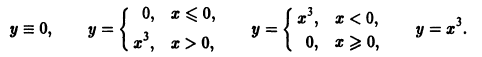
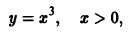
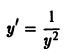
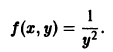
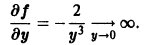
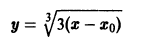
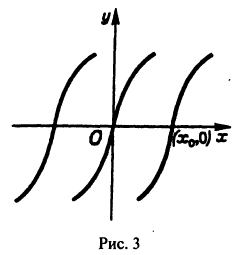
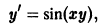
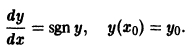

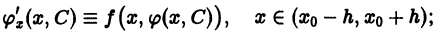
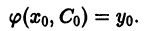
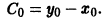
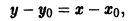

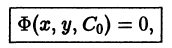
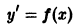
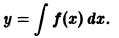
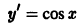
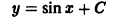
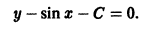
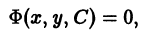

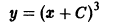
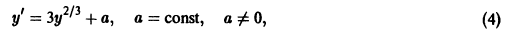
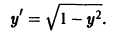

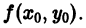
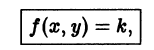
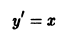
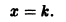
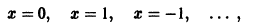
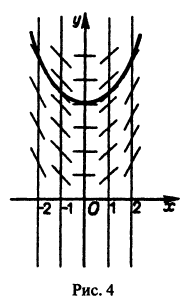
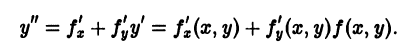
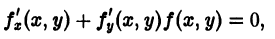
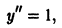


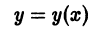
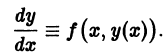
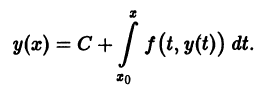
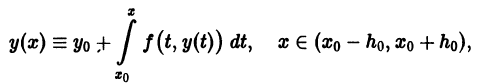
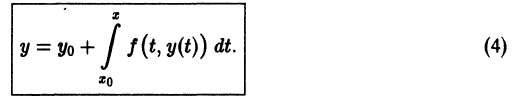
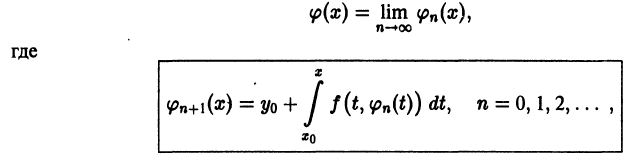
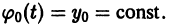
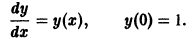
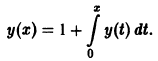
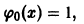
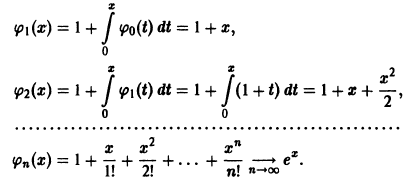


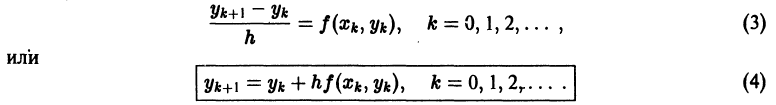
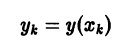
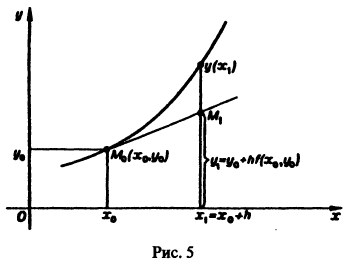
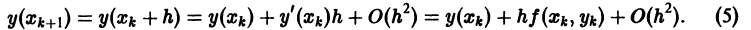
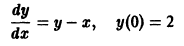
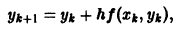
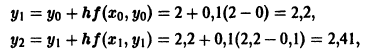
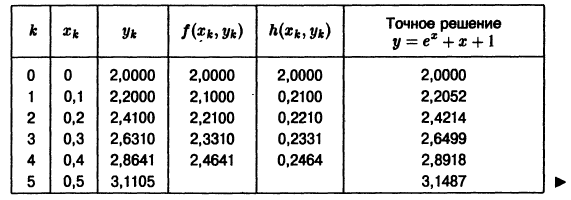
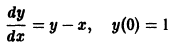
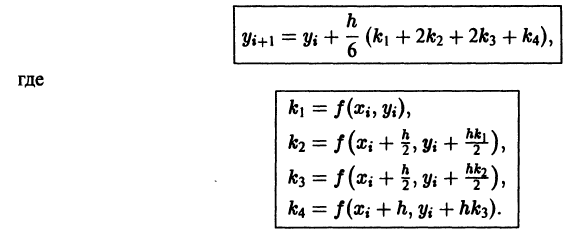

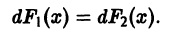

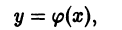
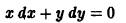
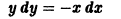
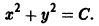
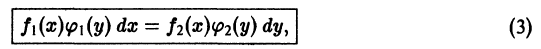
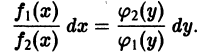
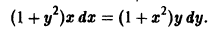
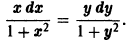


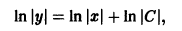
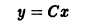
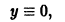
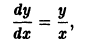
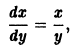



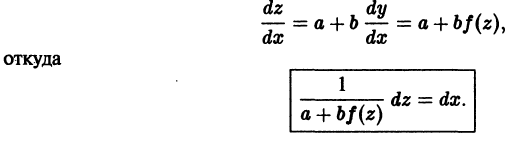
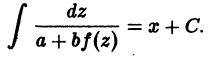
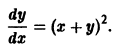
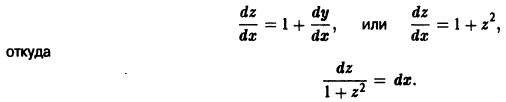

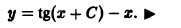

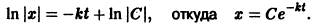


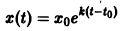

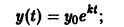
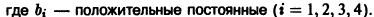
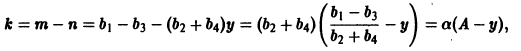
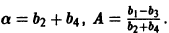
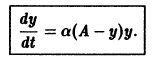

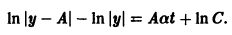
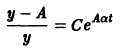
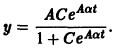
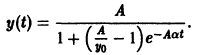
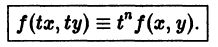
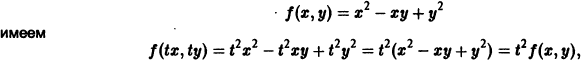
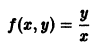
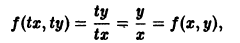
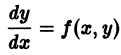
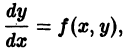
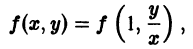

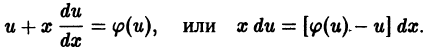
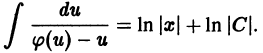
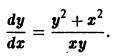
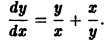

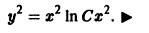
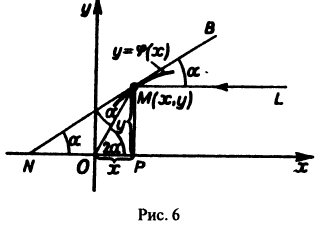
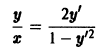
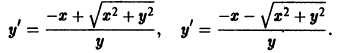
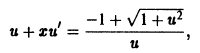
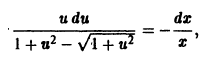
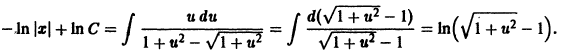

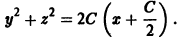
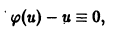
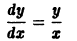
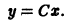
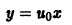

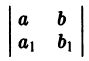 отличен от нуля. Введем новые переменные
отличен от нуля. Введем новые переменные