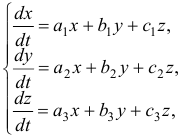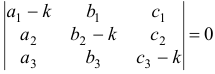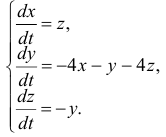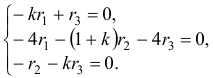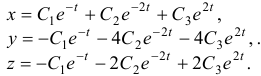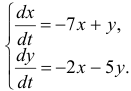Как найти характеристическое уравнение для системы

Характеристическое уравнение составляется для цепи после коммутации. Оно может быть получено следующими способами:

• непосредственно на основе дифференциального уравнения вида (2) (см. лекцию №24), т.е. путем исключения из системы уравнений, описывающих электромагнитное состояние цепи на основании первого и второго законов Кирхгофа, всех неизвестных величин, кроме одной, относительно которой и записывается уравнение (2);
• путем использования выражения для входного сопротивления цепи на синусоидальном токе;
• на основе выражения главного определителя.

Согласно первому способу в предыдущей лекции было получено дифференциальное уравнение относительно напряжения на конденсаторе для последовательной R-L-C-цепи, на базе которого записывается характеристическое уравнение.

Следует отметить, что, поскольку линейная цепь охвачена единым переходным процессом, корни характеристического уравнения являются общими для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение. Поэтому по первому способу составления характеристического уравнения в качестве переменной, относительно которой оно записывается, может быть выбрана любая.

Применение второго и третьего способов составления характеристического уравнения рассмотрим на примере цепи рис. 1.

Составление характеристического уравнения по методу входного сопротивления заключается в следующем:

записывается входное сопротивление цепи на переменном токе;

j w заменяется на оператор р;

полученное выражение приравнивается к нулю.

совпадает с характеристическим.

Следует подчеркнуть, что входное сопротивление может быть записано относительно места разрыва любой ветви схемы. При этом активный двухполюсник заменяется пассивным по аналогии с методом эквивалентного генератора. Данный способ составления характеристического уравнения предполагает отсутствие в схеме магнитосвязанных ветвей; при наличии таковых необходимо осуществить их предварительное развязывание.

Для цепи на рис. 1 относительно зажимов источника

.

Заменив j w на р и приравняв полученное выражение к нулю, запишем

.

(1)

При составлении характеристического уравнения на основе выражения главного определителя число алгебраических уравнений, на базе которых он записывается, равно числу неизвестных свободных составляющих токов. Алгебраизация исходной системы интегро-дифференциальных уравнений, составленных, например, на основании законов Кирхгофа или по методу контурных токов, осуществляется заменой символов дифференцирования и интегрирования соответственно на умножение и деление на оператор р. Характеристическое уравнение получается путем приравнивания записанного определителя к нулю. Поскольку выражение для главного определителя не зависит от правых частей системы неоднородных уравнений, его составление можно производить на основе системы уравнений, записанных для полных токов.

Для цепи на рис. 1 алгебраизованная система уравнений на основе метода контурных токов имеет вид

Отсюда выражение для главного определителя этой системы

.

Приравняв D к нулю, получим результат, аналогичный (1).

Общая методика расчета переходных процессов классическим методом

В общем случае методика расчета переходных процессов классическим методом включает следующие этапы:

1. Запись выражения для искомой переменной в виде
   

   .

   (2)

2. Нахождение принужденной составляющей общего решения на основании расчета установившегося режима послекоммутационной цепи.
3. Составление характеристического уравнения и определение его корней (для цепей, описываемых дифференциальными уравнениями первого порядка, вместо корней можно находить постоянную времени t — см. лекцию №26). Запись выражения свободной составляющей в форме, определяемой типом найденных корней.
4. Подстановка полученных выражений принужденной и свободной составляющих в соотношение (2).
5. Определение начальных условий и на их основе – постоянных интегрирования.

Примеры расчета переходных процессов классическим методом

1. Переходные процессы в R-L цепи при ее подключении к источнику напряжения

Такие процессы имеют место, например, при подключении к источнику питания электромагнитов, трансформаторов, электрических двигателей и т.п.

Рассмотрим два случая:

а)

б) .

Согласно рассмотренной методике для тока в цепи на рис. 2 можно записать

.

(3)

Тогда для первого случая принужденная составляющая тока

.

(4)

,

откуда и постоянная времени .

.

(5)

Подставляя (4) и (5) в соотношение (3), запишем

.

В соответствии с первым законом коммутации . Тогда

,

откуда .

Таким образом, ток в цепи в переходном процессе описывается уравнением

,

а напряжение на катушке индуктивности – выражением

.

Качественный вид кривых и , соответствующих полученным решениям, представлен на рис. 3.

При втором типе источника принужденная составляющая рассчитывается с использованием символического метода:

,

где .

.

Выражение свободной составляющей не зависит от типа источника напряжения. Следовательно,

.

Поскольку , то

.

Таким образом, окончательно получаем

.

(6)

Анализ полученного выражения (6) показывает:

1. При начальной фазе напряжения постоянная интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим.
2. При свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своей наибольшей величины.

Если значительна по величине, то за полпериода свободная составляющая существенно не уменьшается. В этом случае максимальная величина тока переходного процесса может существенно превышать амплитуду тока установившегося режима. Как видно из рис. 4, где

, максимум тока имеет место примерно через . В пределе при .

Таким образом, для линейной цепи максимальное значение тока переходного режима не может превышать удвоенной амплитуды принужденного тока: .

Аналогично для линейной цепи с конденсатором: если в момент коммутации принужденное напряжение равно своему амплитудному значению и постоянная времени цепи достаточно велика, то примерно через половину периода напряжение на конденсаторе достигает своего максимального значения , которое не может превышать удвоенной амплитуды принужденного напряжения: .

2. Переходные процессы при отключении катушки индуктивности от источника питания

При размыкании ключа в цепи на рис. 5 принужденная составляющая тока через катушку индуктивности .

,

откуда и .

В соответствии с первым законом коммутации

.

Таким образом, выражение для тока в переходном режиме

и напряжение на катушке индуктивности

.

(7)

Анализ (7) показывает, что при размыкании цепей, содержащих индуктивные элементы, могут возникать большие перенапряжения, которые без принятия специальных мер могут вывести аппаратуру из строя. Действительно, при модуль напряжения на катушке индуктивности в момент коммутации будет во много раз превышать напряжение источника: . При отсутствии гасящего резистора R указанное напряжение прикладывается к размыкающимся контактам ключа, в результате чего между ними возникает дуга.

3. Заряд и разряд конденсатора

При переводе ключа в положение 1 (см. рис. 6) начинается процесс заряда конденсатора:

.

Принужденная составляющая напряжения на конденсаторе .

Из характеристического уравнения

определяется корень . Отсюда постоянная времени .

.

При t=0 напряжение на конденсаторе равно (в общем случае к моменту коммутации конденсатор может быть заряженным, т.е. ). Тогда и

.

Соответственно для зарядного тока можно записать

.

В зависимости от величины : 1 — ; 2 — ; 3 — ; 4 — — возможны четыре вида кривых переходного процесса, которые иллюстрирует рис. 7.

При разряде конденсатора на резистор (ключ на рис.6 переводится в положение 2) . Постоянная времени .

Тогда, принимая, что к моменту коммутации конденсатор был заряжен до напряжения (в частном случае ), для напряжения на нем в переходном режиме можно записать

.

Соответственно разрядный ток

.

(8)

Как видно из (8), во избежание значительных бросков разрядного тока величина должна быть достаточно большой.

В заключение отметим, что процессы заряда и разряда конденсатора используются в генераторах пилообразного напряжения, широко применяемых в автоматике. Для этого ключ в схеме на рис. 6 заменяется на электронный.

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
3. Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.

1. Составить характеристическое уравнение для цепи на рис. 1, используя выражение входного сопротивления относительно места разрыва ветви с резистором .
2. Может ли в одной части линейной цепи протекать колебательный переходный процесс, а в другой – апериодический?
3. Для чего в схеме на рис. 5 служит цепочка, состоящая из диода и резистора R?
4. Почему можно разрывать ветвь с конденсатором и нельзя – ветвь с индуктивным элементом?
5. Почему корни характеристического уравнения не зависят от того, относительно какой переменной было записано дифференциальное уравнение?
6. Для цепи на рис. 8 составить характеристическое уравнение и определить, при каких значениях переходный процесс в ней будет носить апериодический характер, если .

Ответ: .

Определить в цепи на рис. 9, если , , , .

Ответ: .

Видео:Характеристическое уравнение в ДУСкачать

Решение систем дифференциальных уравнений с помощью характеристического уравнения

Пусть дана однородная система

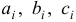
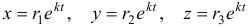
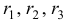
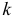
где — постоянные. Будем искать частные решения системы в виде , где и — неопределенные коэффициенты, которые следует найти. Уравнение

называется характеристическим уравнением системы. Отыскав корни этого уравнения, и поочередно подставляя их в исходную систему, определим коэффициенты .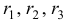

Пример №1

Найти общее решение системы

Решение:

Система в данном случае имеет вид:

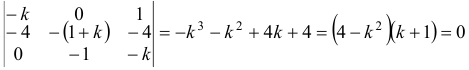
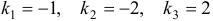
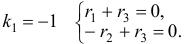
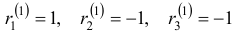
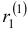
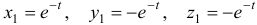
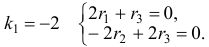
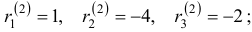
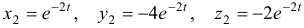
Характеристическое уравнение имеет корни . Для Решением этой системы будут, например, числа (здесь выбрано произвольно). Следовательно, . Для Решая эту систему, получим тогда .

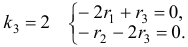
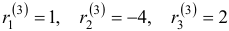
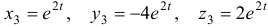
Наконец, для Здесь можно положить и будем иметь .

Общее решение данной системы дифференциальных уравнений таково:

Пример №2

Решение:

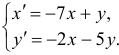
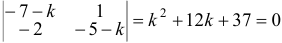
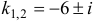
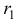
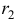
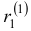
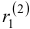
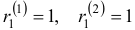
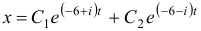
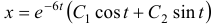
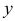
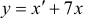
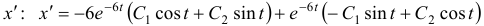
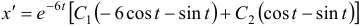
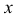
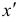
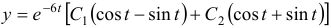
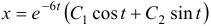
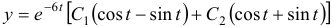
Чаще системы дифференциальных уравнений записывают в виде: Составим характеристическое уравнение и найдем его корни . Так как эти корни комплексные, система уравнений будет иметь комплексные коэффициенты и даст комплексные значения для чисел и . В этом случае, учитывая возможность произвольного выбора и , целесообразно сразу положить и, записав функцию или, что то же самое, , найти функцию , используя первое уравнение системы: . Для этого найдем или . Подставляя и в первое уравнение системы, получим . Общим решением системы будет и .

На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:

Возможно вам будут полезны эти страницы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Портал ТОЭ

6.2 Классический метод расчёта переходных процессов

Анализ переходного процесса в линейной цепи с сосредоточенными параметрами R , L , C (рис. 6.2 ) сводится к решению линейных неоднородных уравнений, выражающих законы Кирхгофа.

где i ( t ) – переходный ток.

Дифференцированием приводим это уравнение к неоднородному дифференциальному уравнению 2-го порядка:

Порядок дифференциального уравнения определяется числом накопителей энергии в цепи.

Решение дифференциального уравнения:

где i _пр ( t ) – частное решение неоднородного уравнения, принуждённая составляющая, ток в установившемся режиме, когда переходный процесс закончен (при t = ∞ );
i _св ( t ) – общее решение однородного уравнения, свободная составляющая, ток во время переходного процесса, возникающий вследствие изменения электрических и магнитных полей.

Таким образом здесь используется метод наложения. Физически существует только i ( t ) , а разложение его на i _пр и i _св является математическим приёмом, облегчающим расчёт переходного процесса.

Расчёт принуждённой составляющей сводится к расчёту по известным методам установившегося значения искомой величины в схеме после коммутации.

Для расчёта свободной составляющей следует найти корни характеристического уравнения p _k и n постоянных интегрирования A _k .

Если характеристическое уравнение

имеет n различных корней p _k ( k = 1 , 2 , … ,n ) , то

Корню p _k кратности m _k ≥ 1 соответствует слагаемое свободной составляющей вида

Чтобы определить постоянные интегрирования A _k , необходимо знать значения искомой величины и всех её производных до ( n − 1) порядка включительно в момент времени t = 0+ . Для их определения используются законы коммутации.

Составление характеристического уравнения

Составляем уравнение электрического состояния цепи для свободного режима (т.е. при устранении вынужденной (принуждающей) силы). Это соответствует схеме с исключёнными источниками – источники ЭДС закорачиваются, ветви с источниками тока размыкаются.

Например для рис. 6.3 :

Корни характеристического уравнения – собственные частоты цепи, т.к. они определяют характер свободных процессов.

Степень характеристического уравнения может быть определена по электрической схеме без составления уравнения: она равна числу основных независимых начальных условий в послекоммутационной схеме после максимального её упрощения и не зависит от числа ЭДС в схеме.

Упрощение заключается в том, что последовательно и параллельно соединённые реактивные элементы должны быть заменены эквивалентными.

Рассмотрим схему на рис. 6.4 . Три реактивных элемента в упрощённой схеме определяют три независимых начальных условия, т.е. порядок характеристического уравнения равен трём.

Свободный процесс происходит в цепи, освобождённой от источников энергии, поэтому свободные токи не могут протекать сколь угодно долго в цепи, где есть активные элементы. Свободные токи должны затухать, в связи с этим действительные части корней p _k характеристического уравнения должны быть отрицательными.

Так, при наличии одного корня p = − a

💡 Видео

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Видеоурок "Нахождение частных решений по виду правой части"Скачать

Собственные векторы и собственные значения матрицыСкачать

Решение матричных уравненийСкачать

Собственные значения и собственные векторы матрицы (4)Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Собственные векторы и собственные числа линейного оператораСкачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Системы дифференциальных уравнений. Часть 2Скачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Собственные значения и собственные векторыСкачать

Как найти определитель матрицы 2х2, 3х3 и 4х4Скачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Найти общее решение уравнения в частных производных первого порядка.Скачать